FDA发射干扰机对无源雷达干涉仪测向系统的欺骗机理
2020-02-12王博谢军伟葛佳昂张晶
王博 谢军伟 葛佳昂 张晶
(1.空军工程大学 防空反导学院,陕西 西安 710051;2.陕西交通职业技术学院 公路铁道学院,陕西 西安 710018)
得到广泛应用的相控阵存在不能有效控制发射波束距离指向的问题。2006年,FDA(Frequency Diverse Array)阵列作为一种距离-角度二维相关波束形成技术由Antonik等[1]在雷达会议上首次提出。与相控阵雷达(Phased Array,PA)通过移相器在阵元间引入固定相位差的电扫描方式不同,FDA阵列通过在阵元间引入一个相比载频而言大小可忽略的固定频偏实现了具有更高自由度的时间-距离-角度三维相关波束指向[2- 6]。雷达电子战中,基于FDA阵列的干扰机其辐射信号被敌方预警探测雷达接收后,由于FDA阵列方向图的时间-距离-角度相关特性,可以在敌方雷达对我方干扰机测角、测速的过程中实现有效欺骗,从而保护我方干扰机。
2017年,Abdallla等[7]系统阐述了基于FDA阵列实现干扰抑制的作用机理,指出FDA在多径干扰抑制、有源干扰抑制等方面具有独特的优势。许京伟等[8- 10]利用FDA-MIMO发射-接收空间角频率的相对关系进行欺骗干扰鉴别,兰岚等[11]提出了一种基于FDA-MIMO结构的欺骗干扰抑制方法,都取得了较好效果。2018年,国内学者[3- 5]发表了多篇综述性文章,对FDA的研究现状进行了系统总结,分析了FDA在射频隐身雷达中的应用前景。而基于FDA方向图的“弯曲”特性,形成虚拟辐射源从而实现对敌方探测雷达的角度欺骗,无疑是实现射频隐身的重要方法[12]。利用发射方向图的弯曲现象,文献[13]从原理上分析了FDA阵列对振幅法测向实现角度欺骗的可能性。在此基础上,本研究通过定量仿真,分析FDA阵列对测向系统及定位系统的欺骗效果。
1 FDA阵列结构
N阵元的FDA阵列结构[1]如图1所示。
设载波频率为f0,第n个阵元的载频为
fn=f0+xnΔf
(1)
式中:n=1,2,…,N-1;xn表示编码系数,xn=n时即为基本FDA阵列,xn=lg(n+1)时得到对数FDA阵列(lg-FDA),xn=sinn时得到正弦FDA阵列(sin-FDA),xn=1/(n+1)时得到倒数FDA阵列(reciprocal-FDA)[14]。
窄带条件下,阵元n的发射信号为
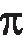
(2)
式中:n=1,2,…,N-1。
阵元n发射信号到达远场观测点(R,θ)的信号形式为
(3)
其中,rn=R-ndsinθ,R为参考阵元到目标点的距离,d为阵元间距,c表示光速。
其发射方向图可以表示为
(4)
一般的,阵元n与阵元0发射的信号传播到远场观测点(R,θ)时所形成的相位差为
Δψ=ψ0-ψn=
(5)
上式第一项为由距离差引起的传统相控阵的相移量;第二项表明Δψ与距离R及频偏Δf相关,这一项是FDA阵列辐射方向图具有距离相关性的基础;由于f0≫N·Δf,第三项在运算中经常可以忽略。
xn=n时,远场观测点(R,θ)处的电场信号为[3,5]
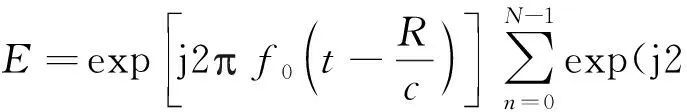
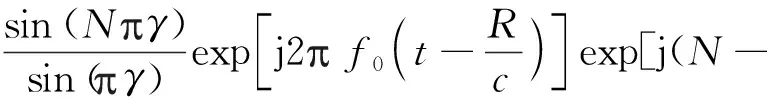
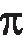
(6)
取其阵列因子AF(t,R,θ):
(7)
取其相位方向图:
(8)
2 FDA干扰机对测向系统的欺骗
2.1 基于欧拉公式的FDA阵列因子
基于图1所示的阵列模型,当采用非线性频控函数时,无法通过级数求和得到形如式(7)sinc函数的阵列因子。因此,本节考虑通过欧拉公式对式(6)进行化简[15]:
(9)
式中,
(10)
根据式(9)可得式(11)所示的基于欧拉公式的FDA阵列因子,以及式(12)所示的基于欧拉公式的FDA阵列相位方向图:
(11)
Φ=
(12)
2.2 FDA阵列对干涉仪测向的角度欺骗
假设基本的两天线干涉仪与图1所示的FDA阵列在X-Y平面内的位置关系如图2所示。
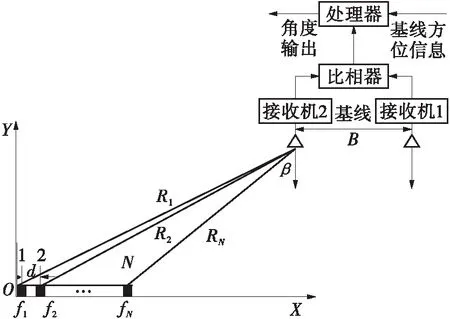
图2 FDA阵列与干涉仪的位置关系
Fig.2 Relationship of position between FDA and the interferometer
远场条件下,假设接收机2的坐标为(xG,yG),则接收机1的坐标为(xG+B,yG)。由式(11)-(12)可得干涉仪比相器输出的相差为
ψ=Φ22-Φ21
(13)
其中,Φ21和Φ22分别表示天线1、2测得的信号相位。
Φ21和Φ22按下式计算:
(14)
其中,
(15)
可得测得的信号到达角β为
(16)
由信号到达角可以进一步计算出虚拟发射机在X轴的位置坐标:
x=xG-yGtanβ
(17)
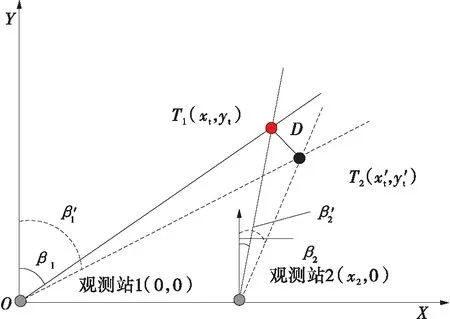
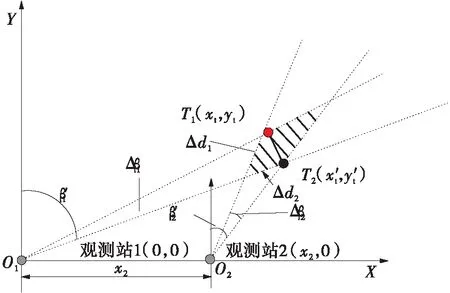
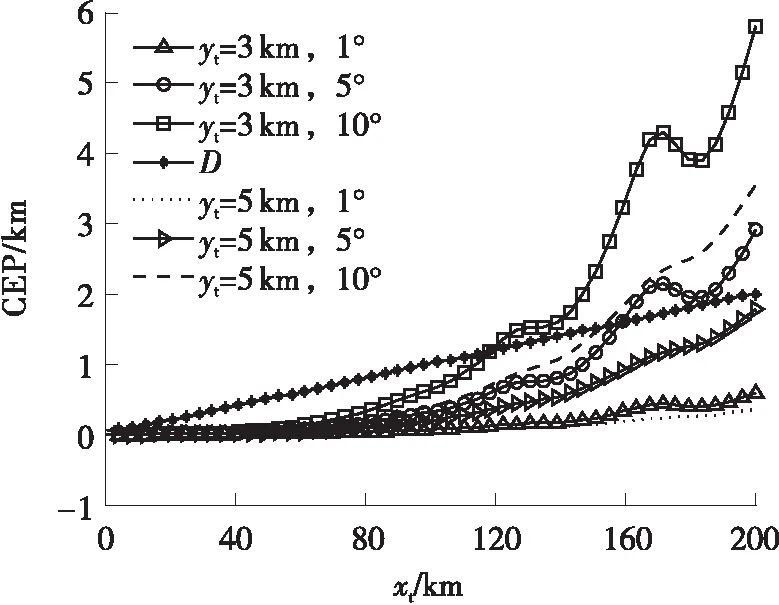
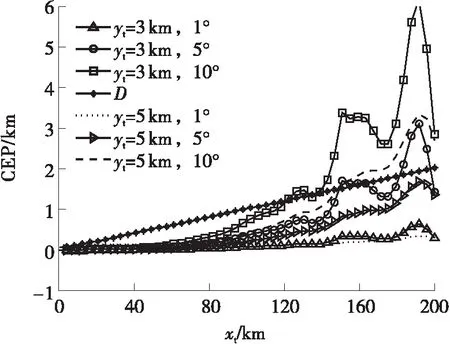
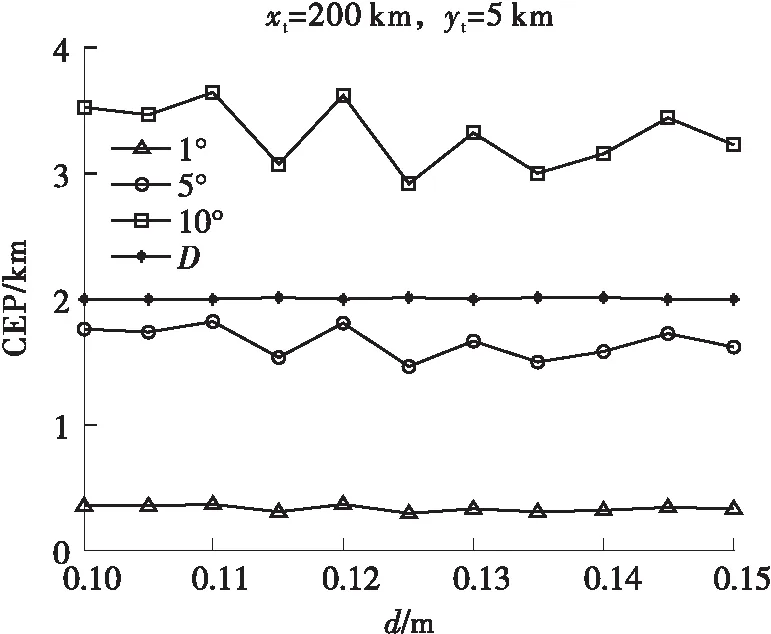
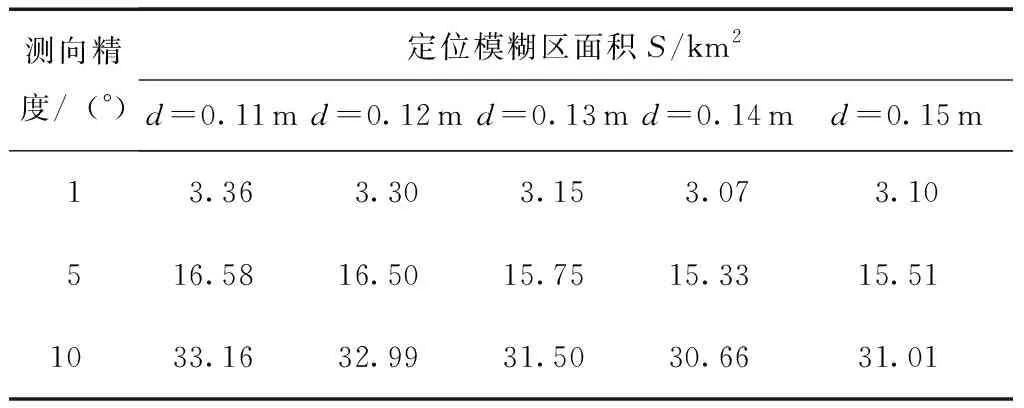
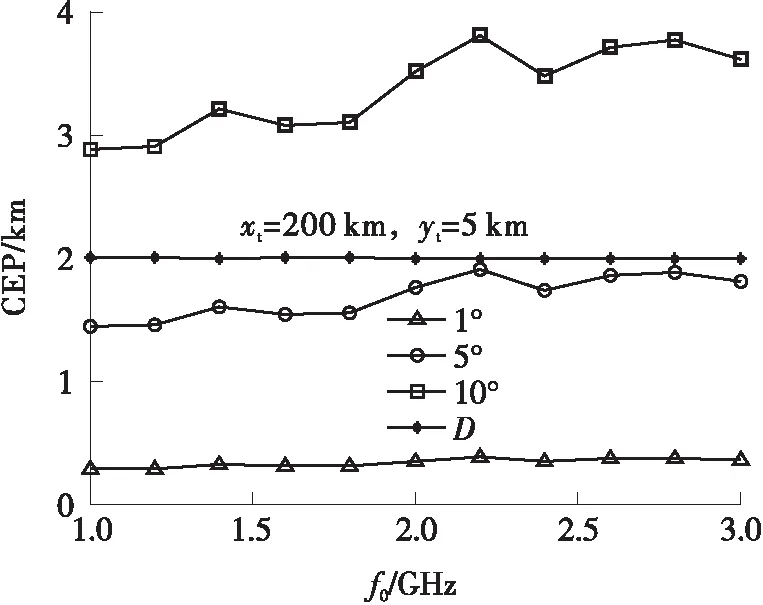
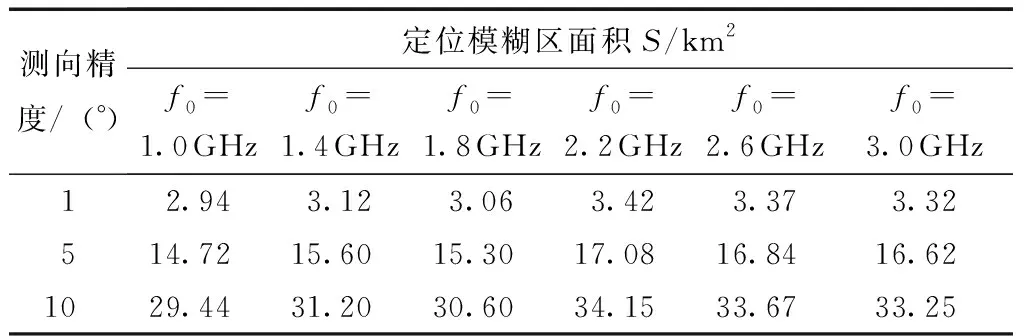
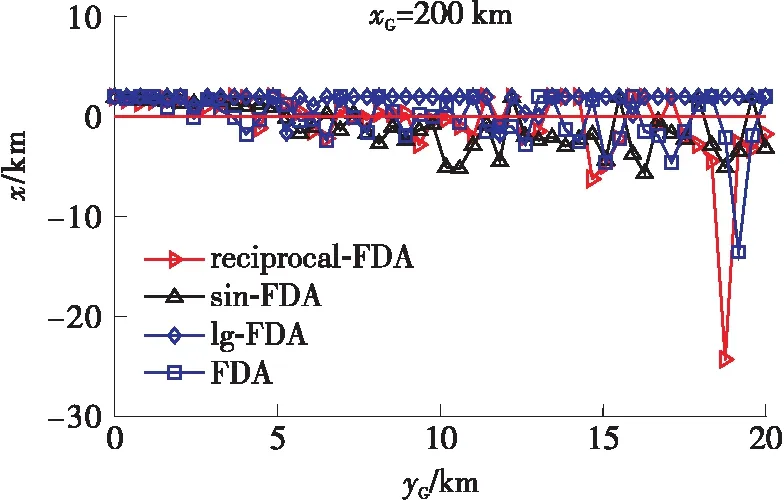
式中,yGtanβ为干涉仪计算出的辐射源所在方向与X轴交点(即为虚拟发射机位置)到干涉仪距离的绝对值。当xG>yGtanβ时,交点在X轴正半轴,x1=xG-yGtanβ为整数,即为虚拟发射机位置坐标;当xG 当我方干扰机掩护作战飞机突防时,干扰机的辐射信号不可避免地会被敌方预警探测雷达所捕获,敌方在测定信号来源方向的同时,可利用多个观测站测得的信号源角度信息,经三角定位解得干扰机的位置信息。图3所示为X-Y平面内基于两个观测站的测向交叉定位原理图[16]。 图3 测向交叉定位原理图 Fig.3 Schematic diagram of direction finding cross positioning 图3中观测站1的坐标为(x1,y1),观测站2的坐标为(x2,y2),干扰机位于(xt,yt)。观测站1、2通过振幅法分别测得辐射源电磁波的到达方向角β1、β2,理想情况下两条射线的交点即为干扰机所在位置。r1和r2分别表示两个观测站到信号源的距离。 根据图3中的几何关系,可得: (18) 改写为矩阵形式: AX=Z (19) 干扰机位置的解析解为 X=A-1Z (20) 将矩阵展开,即可得干扰机的位置坐标: (21) 当自卫式干扰机采用FDA阵列结构对空辐射信号时,其方向图的距离-角度相关特性导致的测角误差,将使测向交叉定位法测定的交点偏离干扰机真实位置,从而实现对测向交叉定位系统的欺骗。 由式(21)可得虚拟干扰机位置T2的坐标: (22) FDA干扰机实际位置与虚拟位置的欧式距离为 (23) 为定量确定FDA干扰机对测向交叉定位法交点坐标的位置欺骗效果,进一步对定位精度进行分析。 图4 FDA干扰机实际位置与虚拟位置的关系 Fig.4 Relationship between the actual position of the FDA jammer and the virtual position (24) 其面积近似为[13]: (25) 由图5可知,当测向定位系统误差较大时,干扰机的真实位置可能落入误差分布区域。由式(25)可知,误差区域的面积与两个观测站之间的间距及测向系统测得的信号到达角有关。上述近似较为粗略,为得到随机分布的定位交点落在干扰机真实位置附近的概率,考虑基于圆概率误差(Circular Error Probable,CEP)半径r0.5对定位误差做进一步的分析。一般可近似认为测向误差服从零均值高斯分布,那么如图6所示,测向交叉定位交点将在以T2为中心的斜椭圆中随机散布,实际中常用圆概率误差半径r0.5作为近似,CEP半径表示50%误差概率时的误差分布圆半径。 图5 测向交叉定位模糊区 图6 测向交叉定位圆概率误差 由式(25)可知: (26) 对上式进行全微分得: (27) 进而有: (28) 上式方差为 (29) 假设两个观测站的测向误差都服从零均值的高斯分布,且相互独立,则其概率密度函数为 (30) 为计算圆概率误差半径r0.5,对上式进行数值积分可近似求得: (31) (32) 将式(24)代入式(32)可得: (33) 按照图2所示的FDA阵列与干涉仪在X-Y平面内的位置关系,以FDA阵列参考阵元为坐标原点建立坐标系,采用表1中的仿真参数,仿真分析FDA阵列对测向系统的欺骗效果。 5.1.1 干涉仪位置对测向欺骗效果的影响 当干涉仪Y轴坐标yG=20 km时,4种FDA阵列对干涉仪测向的角度欺骗效果的仿真结果如图7所示。图7中横坐标为干涉仪的X轴坐标xG,纵坐标为根据干涉仪测向原理得到的虚拟发射机在X轴的交点坐标。 表1 仿真参数表 当干涉仪X轴坐标xG=200 km时,4种FDA阵列对干涉仪测向的角度欺骗效果的仿真结果如图8所示。图8中横坐标为干涉仪的Y轴坐标yG,纵坐标为根据干涉仪测向原理得到的虚拟发射机在X轴的交点坐标。 图7-8中两条横线为FDA阵列参考阵元1(X轴坐标为0)及阵元N(X轴坐标为(N-1)d)在X轴的坐标,当虚拟发射机在X轴的交点坐标落入这个区域时,无法对干涉仪测向实现有效的角度欺骗。 (a)yG=20 km时的欺骗效果 (b)图(a)的局部放大图 图7yG=20 km时不同FDA阵列对测向系统的欺骗效果Fig.7 Deception effect of interferometers based on different FDAs on the direction finding system whenyG=20 km (a)xG=200 km时的欺骗效果 (b) 图(a)的局部放大图 图8xG=200 km时不同FDA阵列对测向系统的欺骗效果 Fig.8 Deception effect of interferometers based on different FDAs on the direction finding system whenxG=200 km 综合分析图7和图8可知,基本FDA阵列的交点坐标曲线最为平滑,角度欺骗效果最佳,但基本FDA阵列方向图存在距离-角度耦合。采用非线性频控函数的FDA阵列中,lg-FDA阵列的虚拟发射机交点坐标随着干涉仪X轴坐标xG的增加而逐渐偏离FDA阵列位置,当xG=200 km时,偏移量为190 m;sin-FDA阵列的虚拟发射机交点坐标随着干涉仪X轴坐标xG的增加在FDA阵列附近变化,当xG=200 km时,偏移量为100 m。当干涉仪X轴坐标xG=200 km时,3种FDA阵列的虚拟发射机交点坐标随着干涉仪Y轴坐标yG的增加而逐渐逼近FDA阵列位置,交点偏移量FDA>lg-FDA>sin-FDA>reciprocal-FDA。reciprocal-FDA的偏移量最小,且reciprocal-FDA发射方向图的距离维及角度维分辨力较低,实际中价值较低,所以本研究后续主要对lg-FDA及sin-FDA两种阵列展开分析。 5.1.2 Δf取值对测向欺骗效果的影响 干涉仪Y轴坐标yG=20 km,其余仿真参数如表1所示时,Δf取值对2种FDA阵列的角度欺骗效果的影响如图9所示。由图9可知,在一定范围内,FDA阵列对干涉仪的角度欺骗效果随着频偏增量Δf的增大而增强。远场条件下,虚拟发射机在X轴的交点坐标逐渐偏离FDA阵列坐标位置,可以实现有效的角度欺骗,且lg-FDA阵列的角度欺骗效果优于sin-FDA阵列。 5.1.3 阵元间距d对测向欺骗效果的影响 干涉仪Y轴坐标yG=20 km、其余仿真参数如表1所示时,阵元间距d对2种FDA阵列的角度欺骗效果的影响如图10所示。由基准载频f0=1 GHz 可知波长λ=0.3 m。图10(b)中d=0.45λ,阵元N的X轴坐标为4.05;图10(c)中d=0.9λ,阵元N的X轴坐标为8.1;图10(d)中d=1.9λ,阵元N的X轴坐标为17.1。由图10中xG=200 km时FDA阵列虚拟发射机的交点坐标可知,在一定范围内交点偏移量随阵元间距的增大而增加。 (a)Δf=1 kHz (b)Δf=2.5 kHz (c)Δf=3 kHz (d)Δf=5 kHz (a)d=0.1 m (b)d=0.45λ=0.135 m (c)d=0.9λ=0.27 m (d)d=1.9λ=0.57 m Fig.10 Deception effect of the value ofdon the direction finding system 基于上述FDA阵列对振幅法测向的欺骗效果仿真,本节以lg-FDA干扰机为例分析其对测向交叉定位系统的定位欺骗性能。建立如图6所示的X-Y坐标系,其中观测站1的坐标为(0 km,0 km),观测站2的坐标为(5 km,0 km),FDA干扰机的纵坐标为5 km,其余参数如表1所示。 5.2.1 干扰机位置、测向精度、频偏增量对定位系统的欺骗影响 图11为lg-FDA阵列在观测站测向精度分别为1°、5°、10°时的圆概率误差半径,图中D值代表FDA干扰机真实位置与虚拟位置的距离。xt=200 km时,计算得到的交叉定位模糊区面积如表2所示。 综合分析图11及表2可知,定位模糊区会随着干扰机距离的增加、测向精度误差的增大以及频偏增量的增大在一定范围内而增大。当测角误差较大时,远场条件下,干扰机真实位置会落入圆概率误差半径r0.5范围内。 (a)Δf=1 kHz (b)Δf=3 kHz (c)Δf=4.5 kHz Fig.11 Deception effect of Δf,σβ,yton direction finding system 表2 不同干扰机位置、测向精度、频偏增量下的模糊区面积S Table 2 Area of fuzzy areaSunder different jammers position,direction finding accuracy,and frequency offset yt/km精度误差σβ/(°)定位模糊区面积S/km2Δf=1kHzΔf=3kHzΔf=4.5kHz311.921.931.6459.619.638.191019.2319.2716.38513.273.293.1516.4316.4415.511032.8532.8831.01 5.2.2 FDA阵元间距d、载频f0对CEP的影响 本例中取xt=200 km、yt=5 km、Δf=4.5 kHz,其余参数如表1所示。图12所示为FDA阵列阵元间距d对测向交叉定位系统的圆概率误差半径CEP的影响;表3为d的取值变化时,定位模糊区面积S;图13所示为FDA阵列载频f0对测向交叉定位系统的圆概率误差半径CEP的影响;表4为f0的取值变化时,定位模糊区面积S。 综合分析图12-13及表3-4可知,远场条件下,当其他参数固定时,随着阵元间距d及载频f0的增加,定位模糊区面积S及CEP取值变动较小;当阵元间距d及载频f0固定时,测向精度误差对CEP的影响更为主要,测向精度误差较大时,干扰机真实位置将落入圆概率误差半径r0.5范围内。 图12 FDA阵元间距d对定位系统的欺骗影响 Fig.12 Deception effect of the FDA array spacingdon direction finding system 表3 不同测向精度、不同阵元间距d取值下的S值 Table 3Svalue under different direction finding accuracy and different array element spacingd 测向精度/(°)定位模糊区面积S/km2d=0.11md=0.12md=0.13md=0.14md=0.15m13.363.303.153.073.10516.5816.5015.7515.3315.511033.1632.9931.5030.6631.01 图13 FDA载频f0对定位系统的欺骗影响 Fig.13 Deception effect of the FDA carrier frequencyf0on direction finding system 表4 不同测向精度、不同载频f0取值下的S值 Table 4Svalue with different direction finding accuracy and different carrier frequencyf0 测向精度/(°)定位模糊区面积S/km2f0=1.0GHzf0=1.4GHzf0=1.8GHzf0=2.2GHzf0=2.6GHzf0=3.0GHz12.943.123.063.423.373.32514.7215.6015.3017.0816.8416.621029.4431.2030.6034.1533.6733.25 5.2.3 FDA干扰机阵元不一致性对欺骗的影响 由图14和图16可知,当考虑阵元不一致性时,远场条件下的偏移量与图8相比增大,但采用4种不同频控函数的FDA阵列其虚拟发射机交点将更多地落入FDA阵列范围。由图15和图17可知,远场条件下,当其他参数固定时,随着阵列载频f0的增加,CEP取值变动较小。当载频f0固定时,测向精度误差对CEP的影响更为主要,测向精度误差较大时,干扰机真实位置将更多地落入圆概率误差半径r0.5范围内。 图14 阵元位置误差下干涉仪位置对测向系统的欺骗效果 Fig.14 Deception effect of interferometer position on direction finding system under array element position error 图15 阵元位置误差下FDA载频f0对定位系统的欺骗影响 Fig.15 Deception effect of the FDA carrier frequencyf0on direction finding system under array element position error 图16 阵元相位误差下干涉仪位置对测向系统的欺骗效果 Fig.16 Deception effect of interferometer position on direction finding system under phase error 图17 阵元相位误差下FDA载频f0对定位系统的欺骗影响 Fig.17 Deception effect of the FDA carrier frequencyf0on direction finding system under phase error FDA雷达能够产生距离-角度-时间相关波束,在雷达目标的距离-方位角联合估计、射频隐身以及前视探测与成像等领域都有广阔的应用前景。文中基于FDA阵列波束指向的距离-角度相关特性,在分析FDA阵列对相位法测角系统欺骗效果的基础上,仿真分析了FDA干扰机对测向交叉定位系统的欺骗效果。由仿真结果可知,测向精度误差对CEP具有较大的影响;误差精度较小时,远场条件下,FDA干扰机对测向及定位系统有着较好的欺骗效果。3 FDA干扰机对定位系统的欺骗

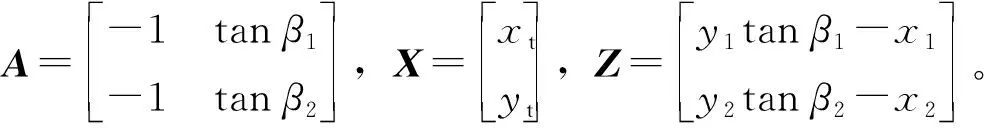
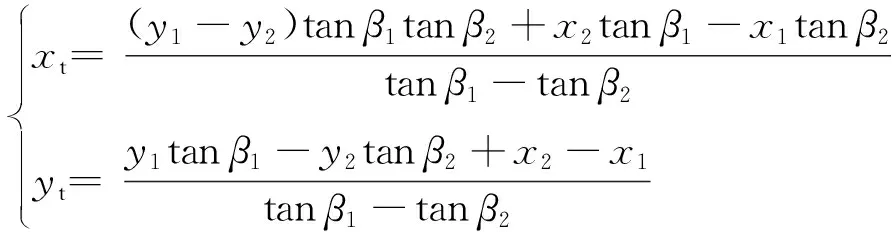
4 定位精度分析

4.1 定位模糊区

4.2 圆概率误差


5 仿真分析
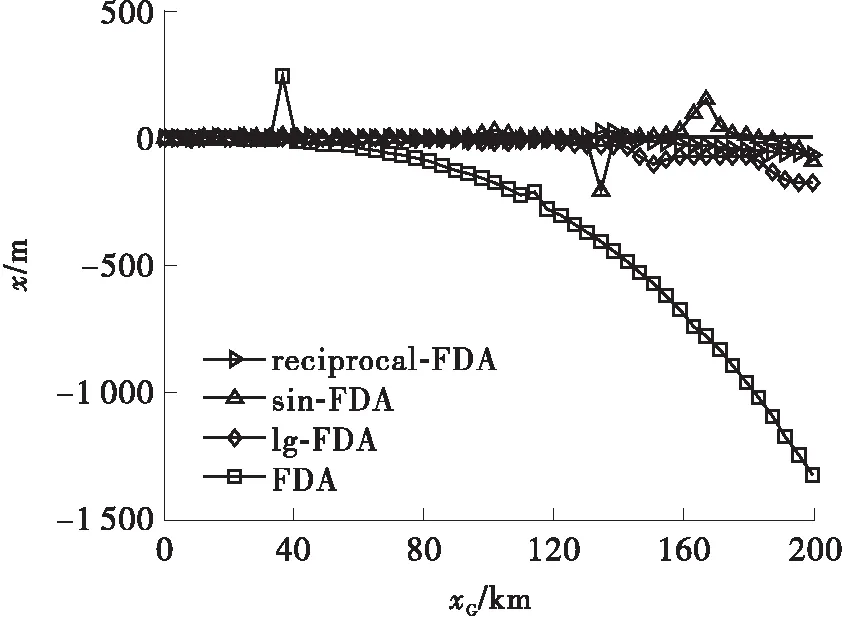
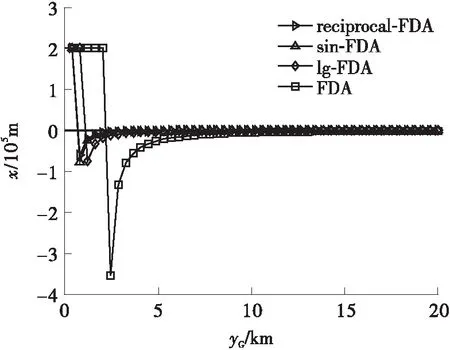
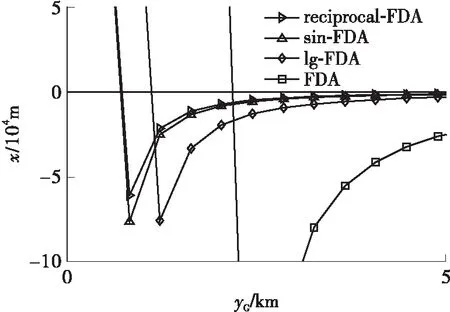
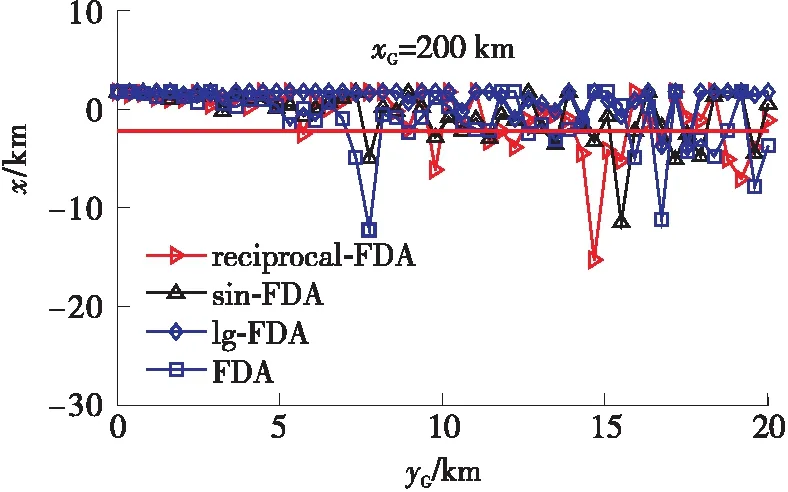
5.1 FDA阵列对测向系统的欺骗分析


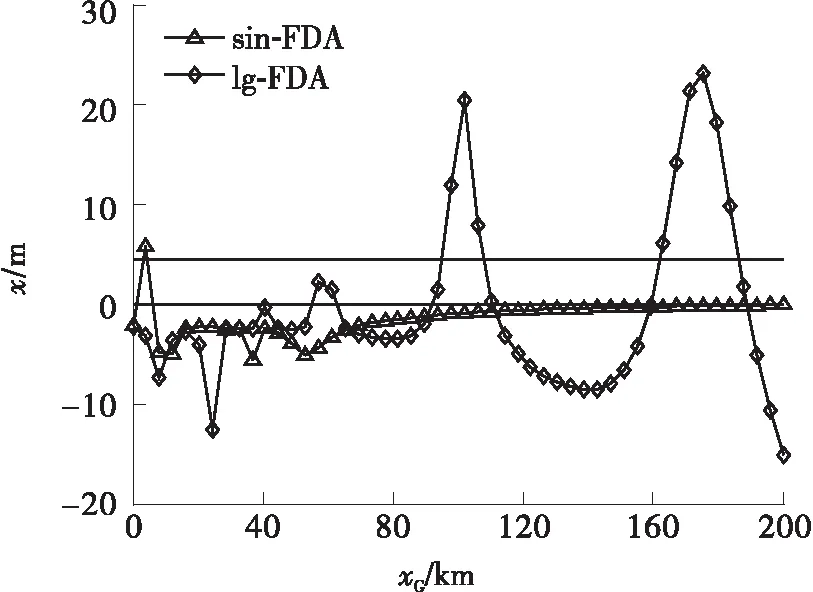
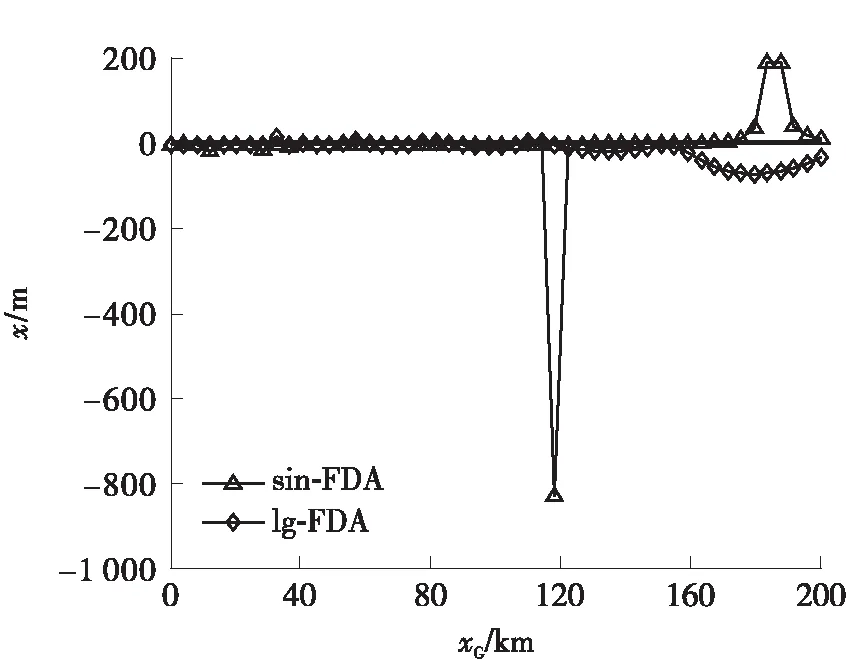
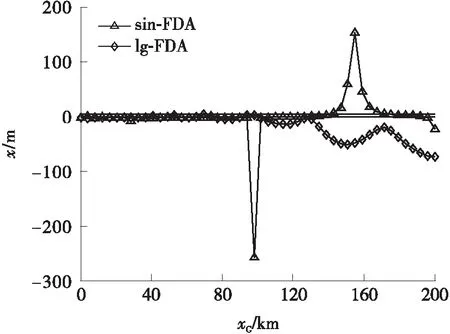
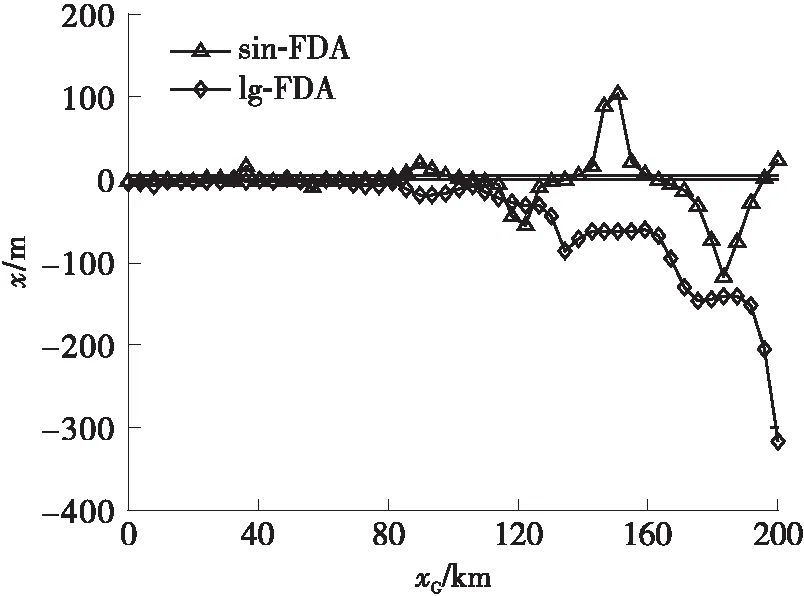

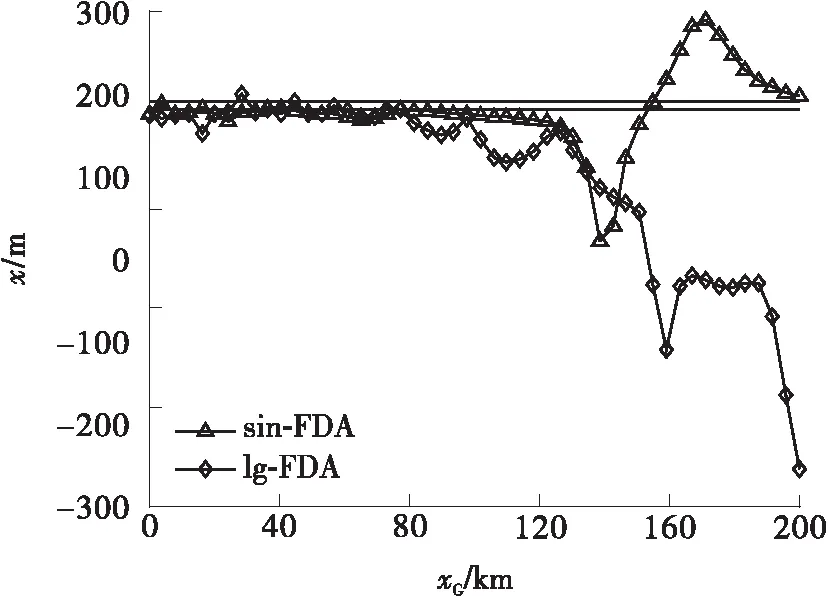
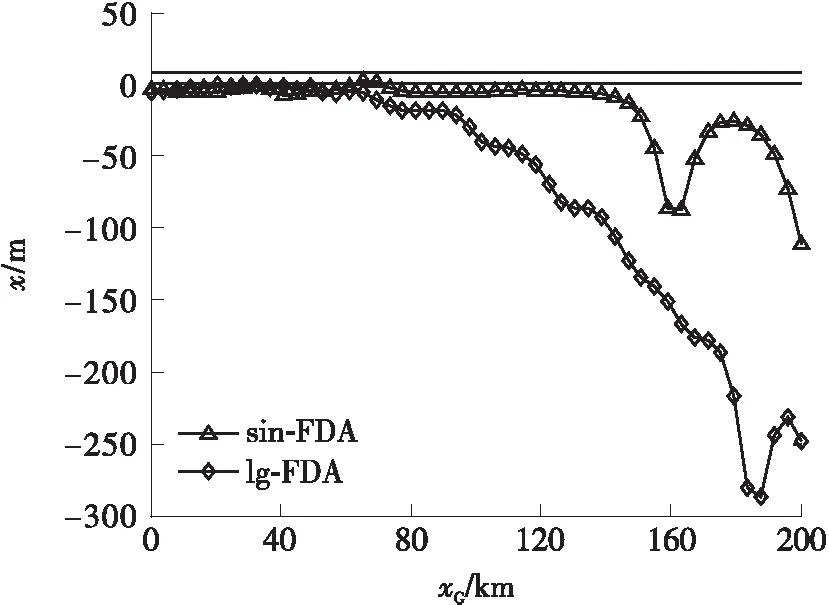
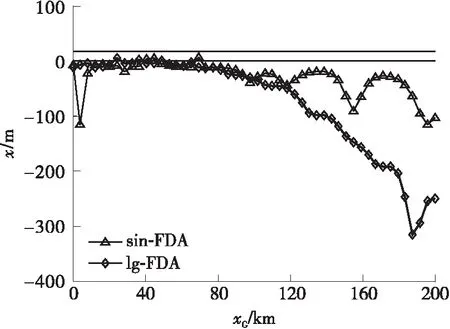
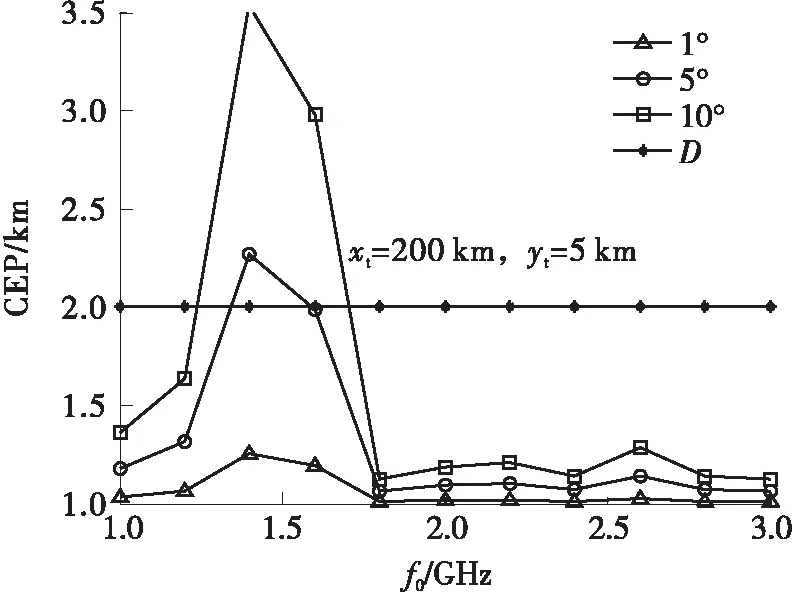
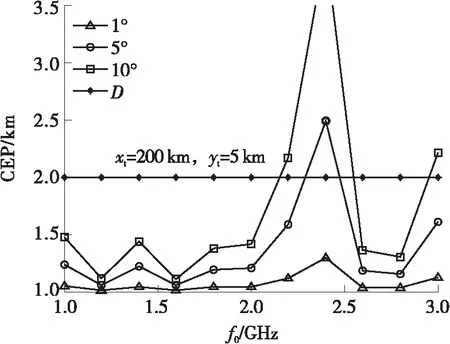
5.2 FDA干扰机对定位系统的欺骗分析
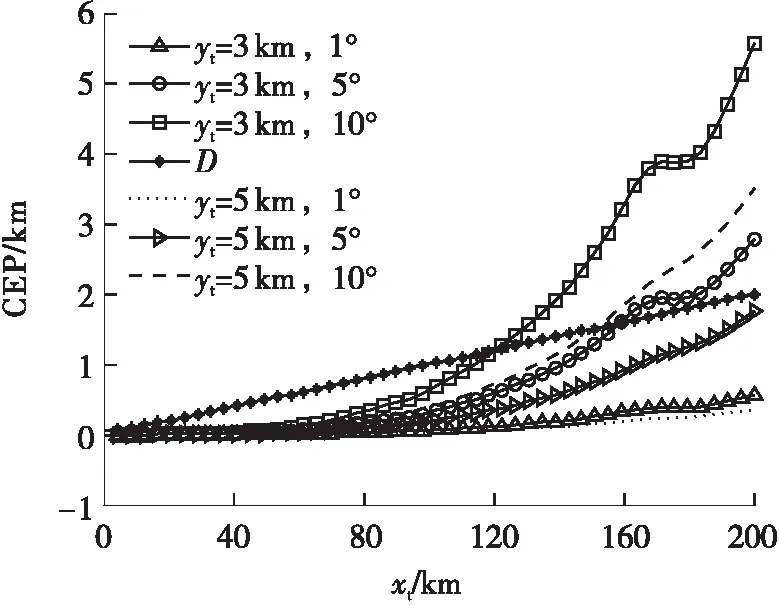

6 结论
