基于模态分析的裂纹齿轮特征识别

2020-02-11岑宇晖徐进友王亮丑述铭白溢文

机械工程师 2020年1期

岑宇晖，徐进友，王亮，丑述铭，白溢文

（天津理工大学a.天津市先进机电系统设计与智能控制重点实验室；b.机电工程国家级实验教学示范中心，天津300384)

0 引言

齿轮传动是应用最广泛的机械传动形式之一，具有效率高、工作性能可靠、传动比恒定等特点。由于工作环境、制造和安装等因素，轮齿极易产生裂纹，裂纹故障是齿轮失效的最主要形式。具有初始裂纹的齿轮随着时间和负载的变化，将会导致断齿等严重后果，严重影响机械设备的安全稳定运行。因此研究裂纹齿轮的传动特点、准确识别裂纹特征尤为重要。

当齿轮产生裂纹时，其啮合刚度的变化会引起振动响应的相应变化，文献[1]～[4]研究了裂纹齿轮的啮合刚度变化规律及对传动系统动态响应的影响，从而作为系统存在裂纹齿轮的判据。文献[5]～[6]以具有裂纹的轮齿为研究对象，探讨了裂纹位置、深度等参数对齿轮的固有频率和振型的影响。

本文以整个齿轮为研究对象，基于有限元分析技术，通过对裂纹齿轮的精确建模，对其动力学参数进行对比分析，从而辨别齿轮裂纹的位置特征。

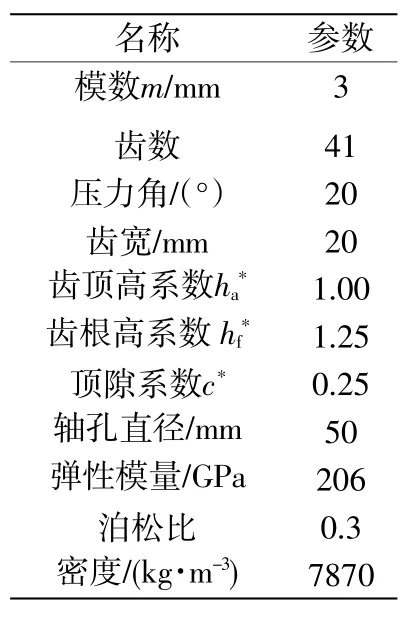
表1 直齿齿轮基本参数

1 齿轮建模

齿轮基本参数如表1所示。在图1所示的坐标系中，Si表示任意半径ri圆上的齿厚，αi、θi为该圆上的压力角和渐开线展角。S、r、α、θ分别为分度圆上的齿厚、半径、压力角及展角。则任意圆上的齿厚可表示为

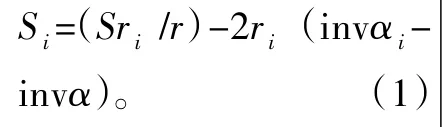
式中：压力角αi=arccos（rb/ri）；rb为基圆半径。

将式（1）离散化，其中ri的变化范围为rb～ra，ra为齿顶圆半径。在ANSYS中，利用APDL语言，编写程序生成渐开线齿廓，并利用布尔运算生成轴孔，形成一个轮齿面。为划分规则的映射网格将齿面分成几个区域，如图2所示。

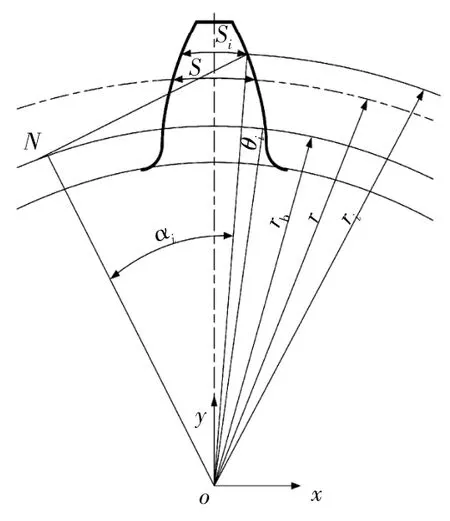
图1 齿轮参数示意图

图2 齿面模型

进一步通过拉伸、旋转复制生成齿轮有限元模型如图3所示。

为对比分析，利用相同办法建立裂纹齿轮模型，裂纹参数定义如图4所示。限于篇幅，文中仅列出齿根处裂纹，裂纹方向为α=60°，深度l=3 mm。所得有限元模型如图5所示。

2 裂纹齿轮模态分析

边界条件取内孔表面节点固定。利用block lanczos法分别求解两种齿轮的模态。

2.1 固有频率和振型对比分析

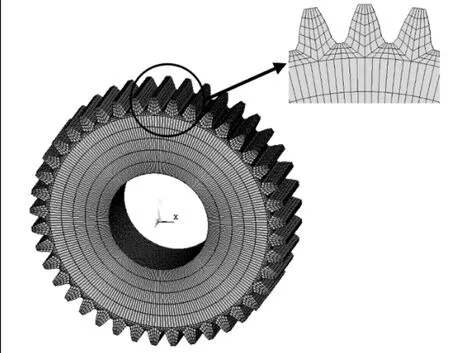
图3 完好齿轮有限元模型

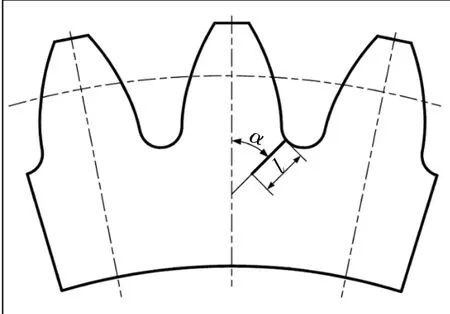
图4 裂纹参数

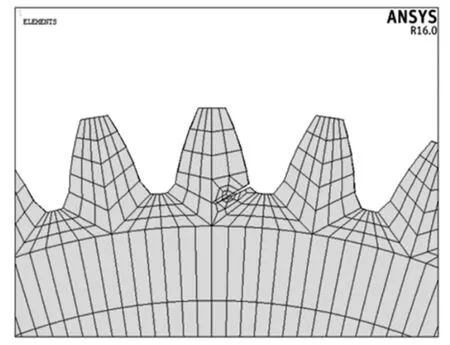
图5 裂纹齿轮有限元模型

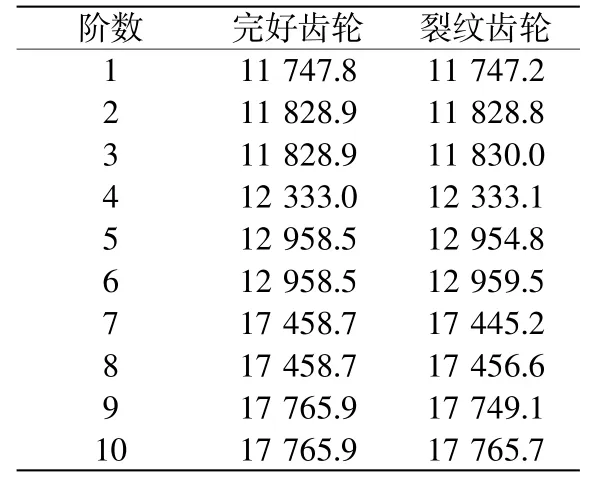
表2 固有频率结果 Hz

完好齿轮和裂纹齿轮的固有频率结果如表2所示。振型云图如图6～图7所示。

从表中可以看出，完好齿轮由于对称性，弯曲振动模式（表2中的2～3阶、5～6阶、7～8阶模态）均为重频，振型相差一个相位。裂纹齿轮由于裂纹破坏了原有的对称性，使得弯曲振动模式的重频特征消失，产生了频率分裂现象[7]。

从完好齿轮和裂纹齿轮的固有频率数值大小上看，二者的变化不明显，振型也无本质区别。因此仅从固有频率和振型无法辨别裂纹的特征。

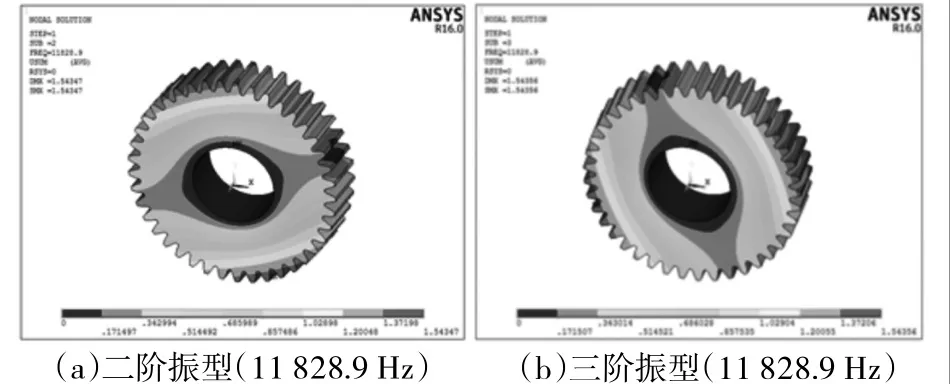
图6 完好齿轮振型

图7 裂纹齿轮振型

2.2 模态曲率分析

本文采用模态曲率作为损伤指标判断裂纹位置[8]。利用ANSYS后处理功能，将振型数据导出，并进行二阶差分运算，获得振型曲线的模态曲率变化规律。二阶中央差分计算公式为

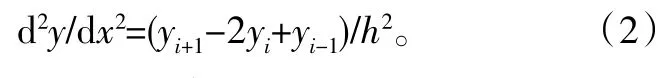
式中：yi为节点i的位移；h为相邻节点之间的距离。

图8～图9为2阶和3阶振型图和模态曲率变化曲线，图中振型位移数据进行了归一化处理，周向位置以x轴为起点，逆时针旋转。

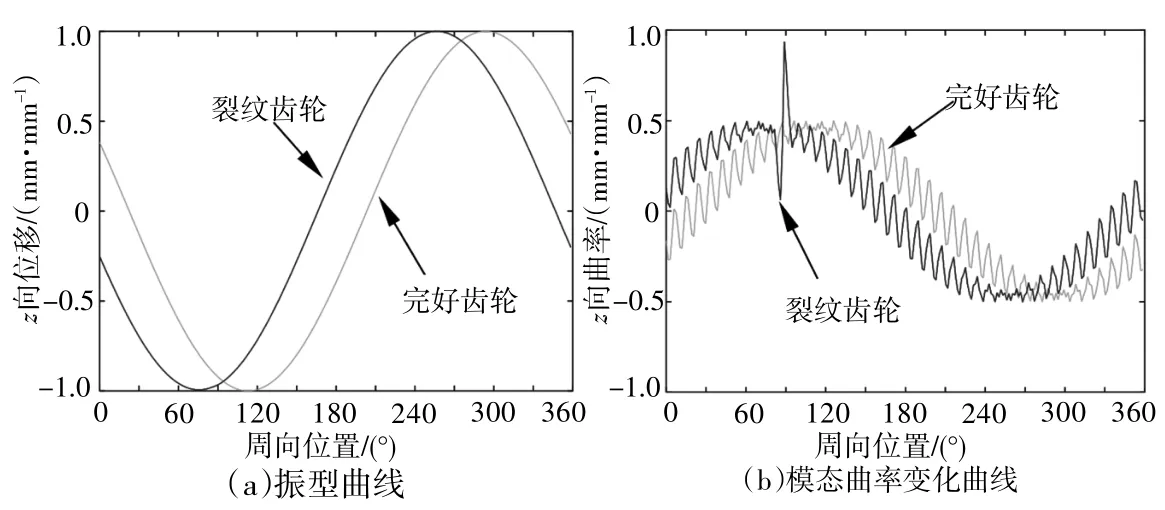
图8 第二阶振型和模态曲率曲线

图9 第三阶振型和模态曲率曲线

从前述结果可以看出，2阶和3阶振型均为1节径的弯曲振动，振型存在一个相位差。在模态曲率变化曲线上可以看出。在90°附近有明显的突变，即为存在裂纹的轮齿附近。从上述结果可以看出，通过模态曲率分析，可以初步判断出裂纹故障所在齿的位置对于不同阶数的振型，其模态曲率的变化趋势基本一致，都是在裂纹处发生突变，利用相同方法可以得到其他模态阶数的模态曲率曲线，可以发现不同阶数的模态曲率的变化幅度不同，随着模态阶数的提高，变化幅度减小。