双跨转子平行不对中故障研究

2020-02-08马俊骁潘宏刚

沈阳工程学院学报（自然科学版） 2020年1期

马俊骁，盛伟，潘宏刚

（沈阳工程学院a.研究生部；b.发展规划处；c.能源与动力学院，辽宁沈阳 110136）

随着火力发电厂高参数、大容量机组的兴建，汽轮机的振动问题显得尤为关键［1］。汽轮发电机组对稳定运行和集中控制水平的要求非常高，其运行可靠性将直接影响全厂的安全性和经济性［2-3］。近年来，随着大型汽轮机组投入使用，转子和静子之间的间隙不断缩小，所引起的振动也越来越剧烈［4］，导致转子不对中故障时有发生。当汽轮发电机组处于临界转速时，转子的振幅急剧增大，造成动静之间碰摩；过临界转速后，振幅减小［5］。转子不对中是最常见的引起汽轮发电机振动故障的原因之一，而转子不对中又以联轴器不对中和轴承不对中为主。转子不对中可由机组的安装误差、缸体变形、热膨胀不均等因素引起。因此，在每一次检修过程中，转子找正的最终目的是使各轴瓦的载荷平均分配［6］。而在一般的检修或者找正过程中，轴系连接的同心度以及平直度不会改变。

大量国内外专家对转子发生不对中故障有着深入的研究。魏伟［7］根据刚性联轴器所连接的柔性转子出现平行不对中，使柔性转子发生形变，进而推导出刚性联轴器平行不对中的激振力表达式。高洪涛、李明［8-9］同时考虑联轴器和轴承的不对中效应，根据平衡条件，列出转子的静平衡方程。Sekhar 和Prabhn［10］对轴上不同位置的联轴器响应做了大量研究。本文以ZT-3型振动仿真试验台作为实验基础，进行了双跨三支点平行不对中转子系统的故障模拟，并将正常情况和发生平行不对中时的转子系统特性进行对比，所得结论对工程实践具有一定的指导意义。

1 联轴器平行不对中机理研究

转子不对中的成因是由于相邻两根转轴轴心线与轴承中心线不在同一条水平线上。联轴器的平行不对中意味着半联轴器的轴线平行于联轴器的设计轴线，且两个半联轴器的中心在径向上不重合。通常用于发电站的联轴器分为齿式联轴器和刚性联轴器。图1介绍了齿式联轴器平行不对中机理。

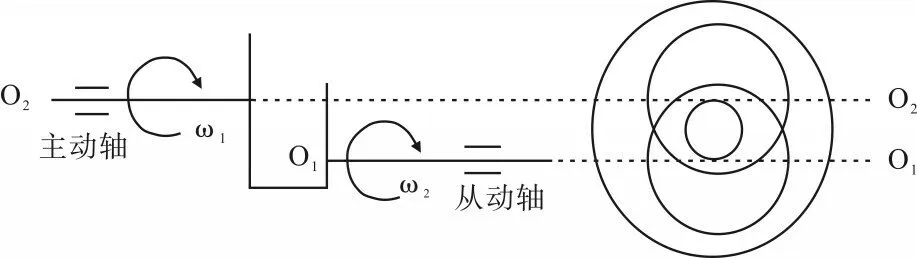
图1 齿式联轴器平行不对中结构

根据文献［11］可知，齿式联轴器中间齿套的中心以径向位移为直径作圆周运动，中间齿套的受力分析如图2所示。

图2 平行不对中受力分析

如图2 所示，取θ为自变量，转轴角速度为ω，所以dθ/dt=ω，所以θ=ωt，则有：

式（1）中，方程组两边对t求一阶导数：

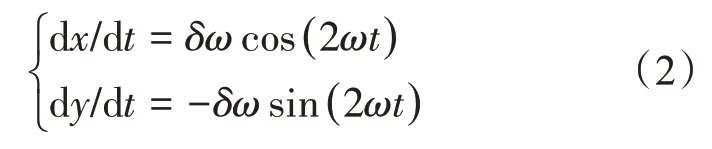
于是得到O3点的线速度为

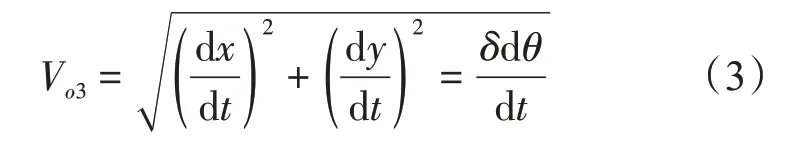
O3点绕圆周中线运动的角速度ωo3为

式中，Vo3为O3点的线速度。

综上所述，联轴器齿套中心O3的旋转角速度是转子角速度的两倍。虽然含有部分谐波分量，但最主要的还是2倍频。

对式（1）和（2）求导：

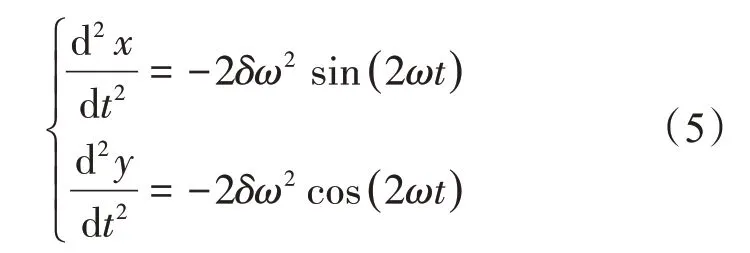
O3点的加速度为

耦合套筒产生的激振力F为

则F对轴施加的激振力为

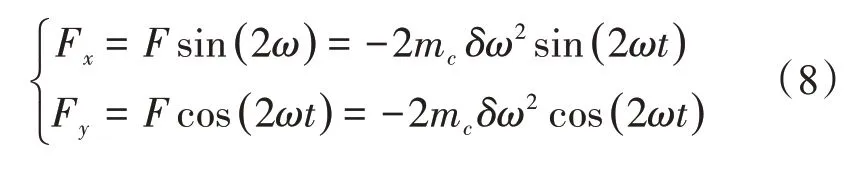
式中，mc为齿套的质量；Fx为x 方向的激振力；Fy为y方向的激振力。

转子轴向的平行位移或角度位移不同，也影响着变形和受力［11］。当转子系统不对中时，转子受径向和轴向的交变力。

当出现转子平行不对中故障时，刚性联轴器上的应力如图3所示。

图3 刚性联轴器所受应力

刚性联轴器的结构及受力分析如图4 所示。O1为驱动轴旋转中心；O2为被动轴的旋转中心；δ为驱动轴与被动轴的延长线的差值；P 为两半联轴器结合处的一点；ω为旋转角速度；ωt为点P的转角。

图4 结构及受力分析

在旋转过程中，被动轴与驱动轴的半径关系为PO2＞PO1。在相互作用力的作用下，半径PO1受压缩，而PO2受拉伸。在PO2上任取一点S，使得PO1=PS。因为δ量一般很小，可以近似为O1S，则

其中一半联轴器的形变量为式（10）所示，另一半与之近似相同。

设系数k是PO1方向上的刚度，根据作用力与反作用力原理可知，PO1方向上的压缩力大小与PO2方向上的拉伸力大小相同，方向相反，其大小F为

则F在垂直方向上的分力为

在水平方向上的分力为

式（12）中，kδ4 表示两轴之间的张力，不随时间变化；kδcos(2ωt)4 表示当转速不同时，激振力和转子上的径向力也不同，转子每旋转一圈，交变两次。

2 平行不对中数值模拟

2.1 模型建立及网格划分

利用数值分析软件ANSYS 中的Geometry 模拟出长轴和轮盘的模型，按实际尺寸设定两根轴的长度及轮盘的直径和厚度，通过拉伸等方法分别对轴承、联轴器、轮盘和轴进行建模。在此基础上，进行网格划分。网格划分是通过ANSYS 中的Mesh模块实现的，有结构性和非结构性两种。结构性网格的优点是使临近点易于识别，大大简化了网格的数据结构，缺点是对不规则的形体生成的网格质量很差；而非结构性网格的优点在于可以处理具有复杂几何形状的模型，因此选择非结构性网格。划分时，将Relevance Center 设置为Fine，其余选项均为默认，绘制网格。绘制完的结果如图5所示。