分散式风电场小型分散集群储能选址定容方法
2020-02-08潘星辰王晓文
潘星辰,王晓文,黄 劲
(沈阳工程学院a.研究生部;b.电力学院,辽宁 沈阳 110136)
随着风电装机容量的不断增加,风电渗透率不断提高,其高不确定性与强波动性的影响不断加剧[1]。在电力系统中,储能可视为一种在不同时间尺度下均能够灵活响应的电源,其规模化应用可解决大规模风电并网消纳问题[2-4],因此储能在风力发电领域的应用前景广阔[5]。国内外学者针对储能配套风电并网发电做了大量研究:文献[6]基于某风电场的风电功率实测数据对VRB 储能系统运行特性及调峰能力进行系统分析,验证了储能系统平抑大规模风电场功率波动参与系统调峰的有效性和可用性;文献[7]阐述了在电力系统短期预测中储能的应用,研究表明储能系统的应用不仅会减缓风速变化带来的功率波动,还能提高风功率预报精度。
本文从对储能系统加入分散式风电场产生的影响进行研究,以总网损最小为指标选址,容量配置转换为能源损失问题,并利用IEEE14 节点系统验证了所提出策略的可行性。
1 分散式风电场并网特性分析
1.1 分散式风电场架构
分散式风电场建立在负荷中心附近,系统的装机容量根据负荷需求的不同具有差异性,一般总装机容量不大于50 MW。分散式风电场中建立储能系统,改善了整个风电场的功率输出特性,有效地实现了能量及功率时间、空间上的转移[8-9],有效地提高储能系统容量配置的合理性,有效地提高风电场可调度性,实现快速的调频调压,为电网提供无功支撑。加入储能系统的分散式风电场架构形式如图1所示。
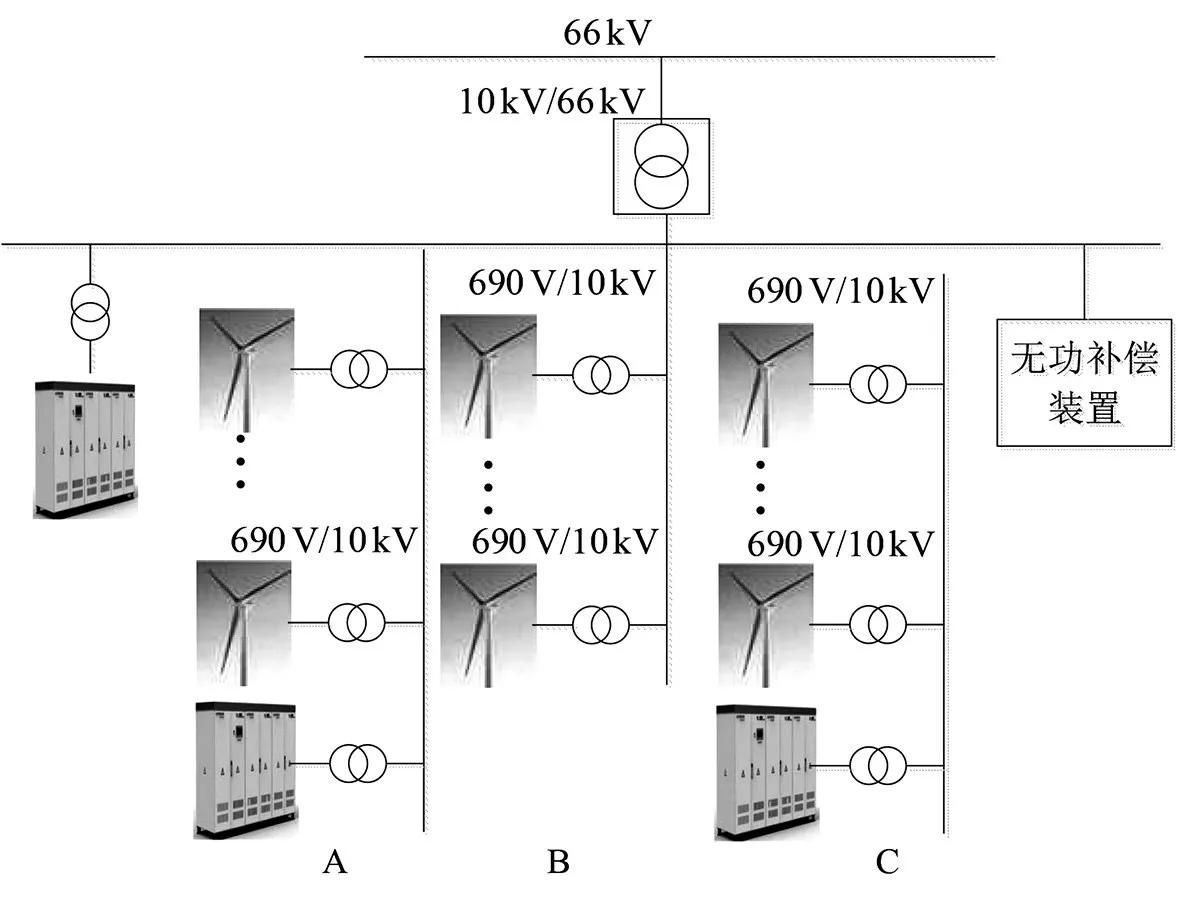
图1 分散式风电场架构
1.2 分散式风电场中并入储能系统后的总网损
分散式风电场中并入储能系统后,并网点输出的有功功率Pbx及无功功率Qbx为
式中,ai=±tan(cos-1φx)为功率因数因子;φx为第x条母线接入点的功率相位差值;Pfx_i为分散式风电场中第i个风电机组向第x条母线输出的有功功率;PESx_i为分散式电场中第i个储能系统向第x条母线输出的有功功率;PMx_i为第x条母线负荷输出的有功功率;Qfx_i为分散式风电场向第x条母线输出的无功功率;QESx_i为分散式电场中集中式储能第x条母线输出的无功功率;QMx_i为第x条母线负荷输出的无功功率。
计算分散式风电场并网后整个网络的有功功率损耗PMf和无功网损QMf分别为

其中,αxy、βxy、γxy和ξxy分别为第x、y条母线之间的功率损耗系数,具体表达式为
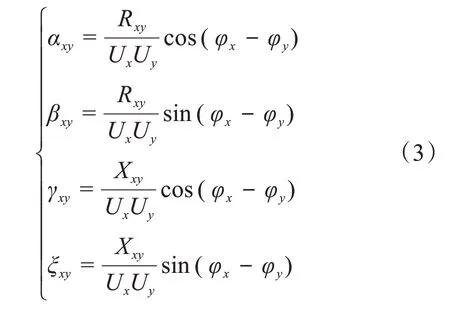
式中,Rxy为第x、y条母线节点之间馈线的阻抗;Xxy为第x、y条母线节点之间馈线的感抗;Ux为第x条母线的电压值;Uy为第y条母线的电压值;φx、φy为第x、y条母线的相位角。
2 分散式风电场储能系统选址定容
2.1 基于权重的网损为目标函数选址
为了考虑储能系统接入后对配网网络损耗的影响,确定分散式风电场储能系统的安装位置,建立了包括有功功率及无功功率在内的网络损耗目标函数,具体表达式为

由于分散式风电场需要对配网提供有功和无功支持,因此在考虑总体网络损耗过程中需要对各条母线的损耗设置权重系数。根据分散式风电场并网作用调节权重系数,求取整个分散式风电场的总网损最小的优化目标为

式中,σPx_i为有功网损的权重系数,σPx_i∈[0,1];σQx_i为无功网损的权重系数,σQx_i∈[0,1];σPx_i和σQx_i满足
以网络损耗最小为优化目标确定各个储能系统的安装位置。
2.2 基于能源损失为目标函数定容
由于风电出力具有随机性,根据历史数据得出风电场出力的极限值和平均值,采用鲁棒优化方法确定出力的最差情况,使得储能系统在优化配置中更为准确地满足并网要求。
由于风力发电机组在运行过程中存在风电出力突变等情况,会带来短期出力预测不准确的情况,进而导致偏差修正不准确等问题,因此可以通过聚类的方式提取经典场景得出出力的极限。
建立分散式风电场基于出力不确定场景的鲁棒自适应数学模型,具体表达式为

为了更准确地求解目标函数,在分散式风电场中根据风电机组的运行状态设置λfx_i,t和θfx_i,t的取值,并从时间和空间两个层面设定不确定度来实现鲁棒优化的保守性。
采用鲁棒自适应调度策略修正式(7),将风力发电短期预测最大值用可调度功率输出的最大值修正,以能源损失为优化目标,具体为

式中,δfx_i为风力发电机组能源损失成本系数。
找出每个风力发电机组最差出力场景,将储能系统的容量配置问题转化成求取能源损失成本的最大-最小问题,具体的目标函数如下:
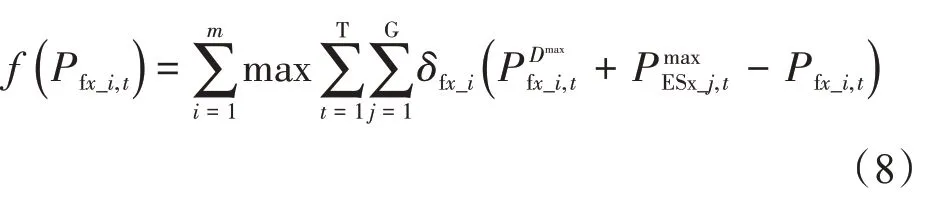
根据式(6)~(8),计算得出最优储能系统个数及各个储能系统的容量需求,具体的表达式为

考虑分散式风电场中各个储能容量配置时考虑的约束条件如下:
1)风力发电系统出力约束

式中,Qfx_i,tmin和Qfx_i,tmax分别是风力发电系统i在时段t的无功出力的下限和上限。
2)节点电压幅值约束
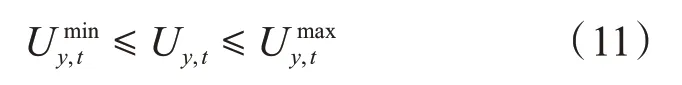
式中,Uy,tmin和Uy,tmax分别是节点y在时段t的电压的下限和上限。
3)储能系统出力约束

式中,PESx_j,tmin和PESx_j,tmax分别是第j个储能系统在时段t出力的下限和上限;PESx_j,t为储能系统实时功率值。
2.3 选址定容规划流程
考虑储能系统接入后分散式风电场并网对网络损耗的影响,以系统总网损最小为目标确定储能系统安装位置,并建立分散式风电场基于出力不确定场景的鲁棒自适应数学模型,以能源损失为优化目标确定储能系统容量,具体步骤如下:
步骤1:根据式(1)计算分散式风电场并入储能系统后,并网点输出的有功功率Pbx及无功功率Qbx值;
步骤2:根据式(2)进一步整理出并网后整个网络的有功功率损耗PMf和无功网损QMf;
步骤3:根据式(4)确定分散式风电场储能系统的安装位置,建立包括有功功率及无功功率在内的网络损耗目标函数;
步骤4:根据分布式并网要求,初始化有功网损权重系数,根据式(5)计算出总网络损耗最小时对应的线路的感抗和阻抗,进一步确定储能系统位置;
步骤5:根据式(6)建立分散式风电场基于出力不确定场景的鲁棒自适应数学模型;
步骤6:采用鲁棒自适应调度策略修正式(7),以能源损失为优化目标,建立目标函数;
步骤7:确定每个风力发电机组最差出力场景,将储能系统的容量配置问题转化成求取能源损失成本的最大-最小问题;
步骤8:根据式(8)计算各个储能系统的功率输出及配置个数;
步骤9:完成储能系统在一个调度周期内合理的容量优化配置。
3 算例分析
以辽宁某地的分散式风电场为研究对象,风电场中包含31 台双馈异步风力发电机组,单机容量为1.5 MW,风电场布局在4 个区域,每个区域的风电机组通过10 kV 集电线并入66 kV 的变电站,并在母线上并入5 MVA 的无功补偿装置。通过mat‐lab 和DIgSILENT PowerFactory 建立分散式风电场电气模型,并将其接入IEEE14 节点进行测试,该系统中共有20 条支路,选取9 节点为SVC 节点,风电场中的4个区域分别选取5、6、9、14节点,设置节点电压上下限为[0.95,1.10],根据分散式风电场运行特性确定储能系统的安装位置和容量。
东北电网用电高峰时段为7:30~11:30、17:30~21:00,高峰持续时间分别为4 h、3.5 h;平时用电时段为5:00~7:30、11:30~17:30、21:00~22:00,平时用电持续时间分别为2.5 h、6 h、1 h;用电谷时为22:00~5:00,持续时间为7 h。东北电网分时电价政策情况如图2所示。
在分散式风电场选址定容过程中,首先考虑分时电价政策对储能系统充放电的影响,选取谷时和平时进行充电,按风电场剩余电量的90%和50%进行充电[10];然后设置权重,并对包含有功和无功的总损耗进行优化求解,确定分散式风电场中储能装置的安装位置,根据风电出力随机性的鲁棒优化确定储能系统的安装容量。

图2 东北电网分时电价政策
根据图3 中得到的分散式风电场典型出力场景中风电场调度值和实际预测出力偏差,考虑风电场的本地消耗按总风电场出力的20%计算。

图3 分散式风电场源典型出力场景曲线
求取分散式风电场总损耗,用以确定分散式风电场位置。根据风电场实际运行情况设置有功网损和无功网损的权重系数0.5,其中,σPx_i=σQx_i满足σPx_i、σQx_i∈[0,1],确定整个分散式风电场有功损耗、无功损耗及总损耗值,如图4所示。
根据风电场实际运行情况设置有功网损和无功网损的权重系数为其中,σPx_i=σPx_i+1、σQx_i=σQx_i+1满足σPx_i、σQx_i∈[0,1]。设置不同的权重确定整个分散式风电场有功损耗、无功损耗及总损耗值如图5所示。
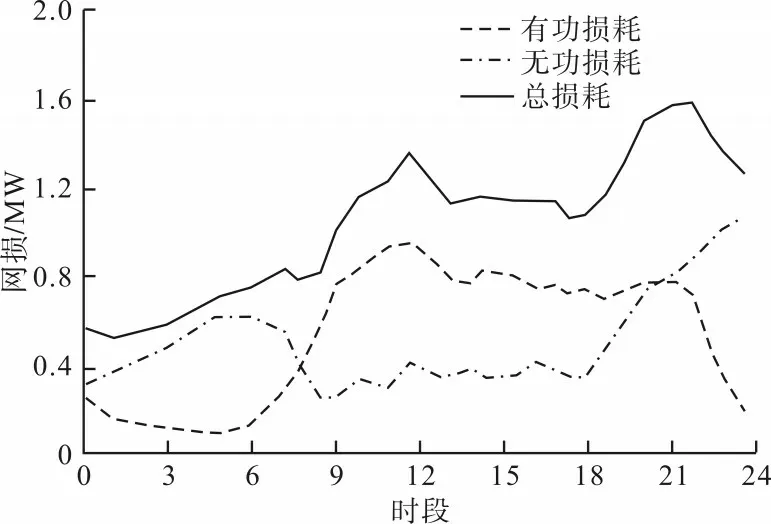
图4 分散式风电场典型日损耗曲线(σPx=0.5)

图5 分散式风电场典型日损耗曲线(σPx=0.8)
根据图4、图5典型损耗确定风电场布局在4个区域内风电机组总运行和损耗情况,合理配置储能系统,具体配置情况如表1、表2所示。
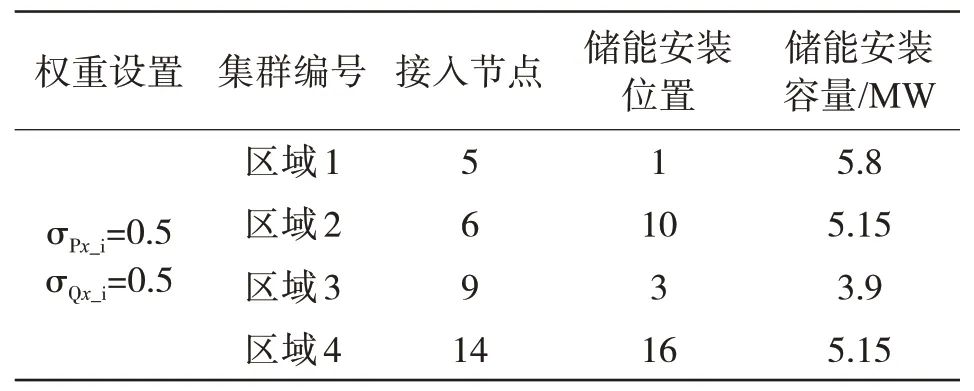
表1 储能系统配置(σPx=0.5)

表2 储能系统配置(σPx=0.8)
从表1和表2可以看出,设置关于损耗的不同权重系数对储能系统的选址定容产生一定的影响,权重不同,容量配置的大小和位置存在一定的差异性。
4 结论
分析了分散式风电场加入储能以后对网损的影响,并提出一种考虑最大接入容量和运行功率因数的分散式风电并网选址定容规划方法。通过仿真验证得到以下结论:
1)通过分时电价政策,确定分散式风电场充放电特性,通过设置权重系数,考虑有功损耗和无功损耗比重对储能系统容量配置的影响。
2)通过鲁棒自适应优化方法,能够确定分散式风电场出力的不确定场景,更为准确地配置储能系统,有效地提高了风电消纳能力,保证了整个分散式风电场的经济运行。
