汽轮机某级质量不平衡分布振动响应分析
2020-02-08孟召军刘彦良郭智娟
孟召军,孙 鑫,刘彦良,郭智娟
(沈阳工程学院a.能源与动力学院;b.研究生部,辽宁 沈阳 110136)
汽轮机是火力发电厂中最核心组成部分,是一种以轴为核心部件的结构复杂的回转机械。近些年来,随着工业生产和科学技术的发展,越来越多的大型机组投入运行。机组容量的增加使结构和系统更加复杂,机械设备的各方面问题都显得特别重要。由于汽轮机兼具功率大、效率高的优点和设备结构复杂、运行环境特殊的缺陷,使得其既对社会具有重要意义又有较高的故障率。由于汽轮机在运行过程中承受较大的热应力、机械应力、离心力以及轴向力的作用,所受应力情况复杂,进而发生振动,产生噪声、碰磨使工作效率降低,严重时汽轮机转子会发生变形甚至断裂。因此,如何降低振动、控制临界转速、降低故障率是设计旋转机械设备的重要课题。
目前,在处理汽轮机转子振动、碰磨等问题上,转子动力学计算方法中的有限元方法具有更加规范、严谨、方便的优点,并且辅以实验数据验证,可以使计算结果更加真实有效。因此,本文利用有限元法来分析汽轮机转子的固有频率和临界转速,并通过模态分析的理论对某亚临界300 MW 汽轮机组的振动、临界转速以及大轴弯曲程度进行分析。
1 模态分析原理
模态分析方法是动力领域研究动力学分析的基础,也是在无外部载荷时对被选取零件结构自由振动的分析。模态是各个固有频率对应的振动形态。模态分析在有限元分析中属于线性分析的范畴,但本文中汽轮机材料具有线性、非线性、恒定或与温度相关的性质。任何单个多自由度的振动系统采用的基本动力学微分方程为
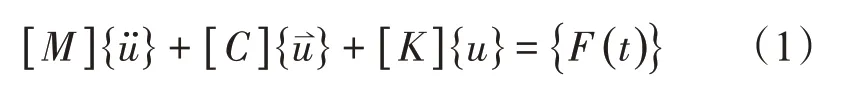
式中,[M]为系统的质量矩阵;[C]为系统的阻尼矩阵;[K]为系统的刚度矩阵;{ü}为加速度向量;{}为速度向量;{u} 为位移向量;{F(t)}为动激励载荷向量。
如果不考虑阻尼对汽轮机转子的影响,且该系统为自由振动,则式(1)变为
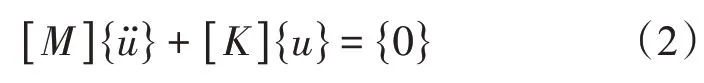
假定系统结构为线性,且为简谐运动,则式(2)变为

利用上述微分方程对本次使用的汽轮机转子的振动特性求解时,应选取布洛克-兰斯洛尔的特征值求解法。
2 模型及约束条件
某国产亚临界300 MW汽轮机高、中压转子的材料为30Cr1Mo1V。汽轮机转子全长为7 868.5 mm,两端轴承的长度为6 100 mm,调节级叶片长度为256.0 mm,中压缸第一级叶片长度为376.0 mm,中压缸末级叶片长度为581.0 mm,如图1 所示。考虑到汽轮机转子轴承的支撑和实际情况,将轴以及叶片等效为圆盘形状,并在中压缸末级相同位置处加装不同质量块,建立有限元模型,如图2 所示。由于尺寸过长,在进行网格划分时为了保证数据的准确性,将模型划分为302 565个网格,如图3所示。

图1 300 MW机组汽轮机高、中压转子结构
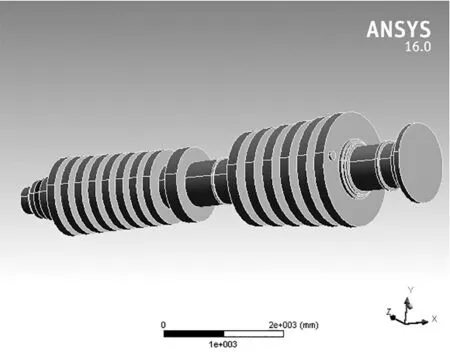
图2 300 MW机组中汽轮机高压、中压转子三维模型

图3 300 MW机组中汽轮机高压、中压转子网格划分
3 模态计算结果分析
表1 为通过ANSYS 软件进行模态分析得到的300 MW 汽轮机组高、中压转子前两阶的固有频率和临界转速。以表1 数据为基础,在中压缸末级相同位置加质量分别为300 g和400 g的质量块,再次分析固有频率和临界转速,如表2 所示。通过分析可知,当加300 g质量块时,固有频率和临界转速都有大幅度的下降;当加400 g质量块时,固有频率和临界转速也有大幅度的下降,且下降幅度较加300 g质量块时要大。

表1 模态分析300 MW机组汽轮机高压、中压转子前两阶固有频率和临界转速数据
图4、图5 和图6 分别为加300 g 质量块、400 g质量块和800 g质量块时前两阶的振型。以未加质量块时汽轮机高、中压转子前两阶的振幅数据作为参考,比较加300 g质量块和加400 g质量块后的振幅变化发现,振幅有较小的增加。利用图4、图5 和图6 的数据进行对比可以得出,在此模型下对中压缸末级增加800 g 以内的质量块,其振幅无明显变化。

表2 加质量块前后数据对比

图4 加300 g质量块时前两阶振型
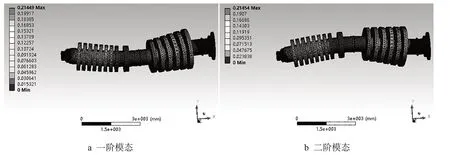
图5 加400 g质量块时前两阶振型

图6 加800 g质量块时前两阶振型
4 结论
1)利用有限元分析软件可以较好地模拟300 MW 汽轮机高、中压转子前两阶固有频率及其临界转速,并分析不平衡质量对临界转速的影响。
2)利用有限元软件能够迅速模拟汽轮机转子的动平衡,当发生质量不平衡时,对大轴弯曲程度作出判断。
3)通过对转子的模态分析以及大轴弯曲程度的判断,对研究汽轮机末级结垢程度有参考意义。
