一种新的降维算法PCA_LLE在图像识别中的应用

蓝雯飞，汪敦志，张盛兰

(中南民族大学 计算机科学学院，武汉 430074)

在机器学习中，随着维度的增加，样本将变得越来越稀疏，在这种情况下，也更容易找到一个超平面将目标分开.然而，在高维空间训练形成的分类器，相当于在低维空间的一个复杂的非线性分类器，这种分类器过多地强调了训练集的准确率甚至于对一些错误、异常的数据也进行了学习，而正确的数据却无法覆盖整个特征空间.故而，这样得到的分类器在对新数据进行预测时将会出现错误.这种现象称为过拟合，同时也是维度灾难的直接体现[1].

在高维度空间，距离度量逐渐失去了度量差异性的能力.由于分类是基于这些距离度量(如欧几里得距离、马氏距离、曼哈顿距离)的，分类算法在低维度空间更容易实现[2,3].

缓解维度灾难的一个重要途经是降维.机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度空间中.目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据.之所以使用降维后的数据表示，是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用(例如图像识别)中造成了误差，降低了准确率；而通过降维，我们希望减少冗余信息所造成的误差，提高识别(或其它应用)的精度.通过降维算法可以寻找数据内部的本质结构特征[4,5].降维已经广泛应用于与数据分析处理有关的生物医疗、基因测试、图像、金融、计算机网络等领域.

YANG P Y等[6]提出了一种新的流式主成分分析算法.流式主成分分析的目标是找到可以解释顺序进入内存的d维数据点的最大方差的k维子空间.大多数流式PCA算法仅使用传入的样本更新当前模型，然后立即转储信息以节省内存.但是，先前流式数据中包含的信息可能很有用.受此想法的启发，作者开发了一种名为History PCA的新型流式PCA算法，可实现此目标.

ZHANG Y S等[7]研究了鲁棒LLE，提出了RLLE算法.在传统的LLE算法中，通过普通最小二乘法计算几何结构，使得嵌入结果对噪声敏感.在RLLE算法中，最小角度回归和弹性网络(LARS-EN)技术用于计算局部结构.此外，提出了一种基于RLLE和支持向量机(SVM)的故障诊断方法，用于机械故障诊断.在合成和实际数据集上进行的实验证明了所提出的方法在故障诊断方面的优点.

图像是高维的数据，通过降维处理，可以降低数据的复杂度，发现数据的内在规律和本质，对于分类也有帮助.人脸具有一种典型的流形结构，人脸数据集是由于内在变量控制形成的非线性流形，人脸图像数据属于采样于高维欧氏空间中的低维流形结构.通过降维，可以描述不同类别样本之间的差异，从而有利于分类.

1 PCA与LLE算法介绍

1.1 PCA算法

主成分分析(Principal Component Analysis，PCA)是一种利用线性映射来进行数据降维的方法，同时去除数据的相关性，以最大限度保持原始数据的方差信息.

给定d维空间中的样本X=(x1,x2,…,xm)∈Rd×m.为了便于后续计算，首先对样本进行中心化:

对其线性变换之后得到d′维空间中的样本：

Z=WTX，

(1)

其中W∈Rd×d′是变换矩阵，W的各列wi与wj正交.Z是样本在新空间中的表达.变换矩阵W可视为d′个d维基向量，zi=WTxi是第i个样本与这d′个基向量分别做内积得到的d′维属性向量.

(2)

PCA原理图可参见文献[5].

1.2 LLE算法

局部线性嵌入(Locally Linear Embedding，LLE)是一种借鉴了拓扑流形概念的降维方法.“流形”是在局部与欧氏空间同胚的空间，它在局部具有欧氏空间的性质.假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中找到低维流形[8].流形学习可以用于实现聚类、分类以及回归.

局部线性嵌入从局部几何结构入手，试图保持邻域内样本之间的线性关系[9].LLE原理图可参见文献[5].

给定d维空间中的样本X=(x1,x2,…,xm)∈Rd×m，LLE先为每个样本xi找到其近邻下标集合Qi，然后计算出基于Qi中的样本点对xi进行线性重构的系数：

(3)

解出wij，于是xi在低维空间的坐标zi可通过下式求解：

(4)

令Z=(z1,z2,…,zm)∈Rd′×m为降维后数据，(Wij)=wij，矩阵M如下：

M=(I-W)T(I-W)，

(5)

则优化问题可重写为：

(6)

可通过特征值分解求解：M最小的d′个特征值对应的特征向量组成的矩阵即为ZT.

过大的降维后维数会导致降维后的数据存在大量多余的噪声信息，为分析处理问题带来麻烦；过小的降维后维数则会导致数据的特征向量缺失，致使降维结果不完善.只有当降维维数与本征维数之间基本保持一致时，降维结果才达到最佳.

2 融合PCA与LLE的降维方法

2.1 模型的提出

PCA考虑的是数据的全局结构，LLE考虑的是数据的局部几何关系，融合两个算法可使两者优缺点互补.

首先对样本中心化，由于中心化只是对样本进行平移，并不会改变样本之间的位置关系，对LLE算法不会有影响.

将LLE算法变为线性的形式，令Z=WTX，(6)式化为：

(7)

结合(2)，(7)式得：

即：

(8)

(8)式可通过特征值分解求解.该式结合了主成分分析(PCA)和局部线性嵌入(LLE)，可以提高分类器的准确率.

2.2 模型求解

令矩阵

G=X(I-γM)XT，

(9)

G=XXT-γXMXT，GT=(XT)TXT-γ(XT)TMTXT=XXT-γXMXT=G，所以G是对称矩阵.对称阵的特征值为实数.

设W的第一主轴方向u1使得u1TGu1最大，则构成一个最大化问题：

maxu1TGu1，s.t.u1Tu1=1.

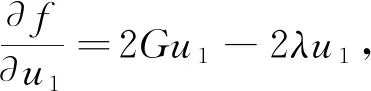
算法流程如下.

输入:样本集X=(x1,x2,…,xm)∈Rd×m;近邻参数k;低维空间维度d'.输出:样本集在低维空间的投影Z=z1,z2,…,zm ∈Rd'×m.过程:对所有样本中心化;for i=1,2,…,m do确定xi的k近邻;求得重构系数wij,j∈Qi;对于j∉Qi,令wij=0;end for从(5)式得到M;从(9)式得到G;对G进行特征值分解,最大的d'个特征值对应的特征向量构成W;Z=WTX;

对于新样本xnew降维，首先减去所有训练样本的均值，再用WT乘以xnew.

3 高维数据降维可视化

图像数据往往是高维的，大量高维样本图像的低维嵌入性特征往往并不直观明显.将手写体图像数据集MNIST利用PCA、LLE降维到三维，对这些三维坐标值和相应的标签，利用Python语言的Matplotlib模块绘制三维散点图像，不同类别用不同颜色表示，如图1～3所示.可以看到，不同类别的样本降维后的坐标点位于低维空间的不同区域，同一类别的样本降维后的坐标点在低维空间基本上汇聚在一起，这说明利用降维对图像进行分类和识别的可行性.

图1 PCA降维Fig.1 Dimension reduction using PCA

图2 LLE降维Fig.2 Dimension reduction using LLE

图3 PCA_LLE降维Fig.3 Dimension reduction using PCA_LLE

通过降维，把图像数据映射到低维空间，能够提取图像特征.从图中可以看到，PCA降维后的数据分布比较均匀，LLE降维后的数据在一些位置比较集中.这是因为PCA是全局性的算法，LLE是局部性的算法.PCA_LLE降维后的数据分布是比较均匀的.

单个阿拉伯数字(0～9)图像理论上是一个高维空间中的低维流形.为直观理解PCA算法、LLE算法对图像数据集的降维效果，选取数据集中标签相同的数字图像30个，分别运用PCA、LLE、PCA_LLE将图像数据降维成两个维度，利用Python语言的Matplotlib模块，以这两个维度的值为坐标，将对应的数字图像显示在平面上，如图4～6所示.

图4 PCA降维结果显示Fig.4 Result of dimension reduction using PCA

图5 LLE降维结果显示Fig.5 Result of dimension reduction using LLE

图6 PCA_LLE降维结果显示Fig.6 Result of dimension reduction using PCA_LLE

图4为数字‘5’PCA降维结果，可以看出相邻的、空间位置比较靠近的图片内容是比较接近的.相似的图片降维后的坐标点互相靠近.图5为数字‘2’LLE降维结果，可以看到，‘2’下面的笔画有个圈的图像降维后汇集在一起，且相似的图像比较靠近.图6为数字‘2’PCA_LLE降维结果，可以看出内容相似的图像降维后的位置比较靠近，且相较于LLE算法，PCA_LLE降维后的数据分布更均匀.

4 实验与分析

4.1 手写体图像识别

4.1.1 实验方案

下载MNIST手写数字图像数据集，加载训练集和测试集.

(1)不进行降维，直接对数据集使用KNN算法分类.

(2)使用PCA、LLE、PCA_LLE三种算法对数据集降维，并训练分类器.调整以下参数：

公式(7)中的参数γ；

降维后的维数d′；

近邻个数k；

并记录相应的准确率，找到使准确率最高的参数值.

4.1.2 实验环境

本文的实验是在Windows10系统下进行的，CPU:Intel(R) Core(TM) i5-6200U，内存4.0GB.使用的编程语言为Python3，开发工具为Anaconda Spyder.

4.1.3 实验结果与分析

不降维，训练样本为5000个，测试样本为10000个时，使用KNN算法进行分类，当KNN算法的近邻数k分别为：4、5、6、10、15时，准确率分别为：0.9312、0.9325、0.9293、0.9251、0.9194.k值如果太小，预测结果就会对近邻的样本点十分敏感，如果近邻的样本点恰巧是噪声，预测就会出错；k太大，近邻中又可能包含太多的其他类别的样本点.

取MNIST数据集的前5000个训练样本进行降维，使用K近邻算法对降维后的数据分类.LLE算法和PCA-LLE算法近邻个数k取值8～12效果较好.k的取值过大，就可能会影响整个流形的平滑性，就不能体现其局部特性，这样会导致LLE算法趋向于PCA算法，甚至丢失流形的一些小规模的结构；而k的取值过小，就很难保证样本点在低维空间的拓扑结构，可能把连续的流形脱节成子流形.PCA-LLE算法当γ=0.2时，分类的准确率最高.

使用PCA和KNN算法进行分类，当降维后的维数分别为：20、30、40、50、70、100时，准确率分别为：0.9287、0.9352、0.9210、0.9099、0.8814、0.8280.使用LLE和KNN算法进行分类，当降维后的维数分别为：40、50、70、100时，准确率分别为：0.9266、0.9273、0.9313、0.9262.使用PCA_LLE和KNN算法进行分类，当降维后的维数分别为：30、35、40、50、70、100时，准确率分别为：0.9457、0.9473、0.9464、0.9448、0.9422、0.9372.

可以看出PCA算法在降维后的维数为30时分类的准确率最高，为93.52%.LLE算法在降维后的维数为70时分类的准确率最高，为93.13%，说明本征维度在70左右.PCA_LLE在降维后的维数为35时分类的准确率最高，为94.73%，说明PCA_LLE算法的效果较PCA和LLE有所提高，而且使用PCA或PCA_LLE降维后的分类准确率比不降维的要好.

10000个新样本的情况下降维时间比较见表1.

表1 新样本降维时间Tab.1 Dimension reduction time of new samples

可见PCA_LLE算法对新样本的降维时间远低于LLE，这是由于它是通过坐标变换把新样本直接映射到低维空间.现有的对流形学习的改进算法，如陈鹏飞等[10]提出的核框架下等距映射与局部线性嵌入相结合的KISOMAPLLE算法，对于新样本降维仍然要寻找它的近邻样本.而PCA_LLE算法不需要寻找近邻，直接通过正交变换矩阵将新样本映射到低维空间，因此，降维时间大大减少.

4.2 人脸图像识别

实验采用ORL人脸图像数据集，该数据集包含40个人的共400张人脸图像，每人10张.对每个人随机选取3张作为训练集，其余7张为测试集.

先对训练集进行降维，降维方案有3种：1)先使用PCA降维，再对结果使用LDA(线性判别分析)降维；2)仅使用PCA降维；3)仅使用LDA降维.降维后，再使用Logistic Regression算法分类.

进行两次实验，每次在每个人中随机选取3张图片作为训练样本.3种方案PCA+LDA，PCA,LDA第一次的分类准确率为：0.90000，0.878571，0.796429；第二次的分类准确率为：0.896429，0.882143，0.742857. PCA降维后的维数为30时，准确率最高.实验结果表明PCA结合LDA的方法准确率更高.

为了比较PCA_LLE算法同PCA、LLE算法在人脸识别中的优劣势，分别使用PCA_LLE+LDA，PCA+LDA，LLE+LDA对训练集降维，再用Logistic Regression算法分类，进行四次实验，准确率见表2.LLE降维后的维数为80时，准确率最高.PCA_LLE降维后的维数设为30.

表2 PCA_LLE、PCA、LLE算法准确率比较

四次实验，PCA_LLE算法的准确率均高于PCA算法和LLE算法.

5 结语

PCA算法在降维时考虑到数据的全局结构，使得整体方差最大化.LLE算法则考虑样本的局部几何结构.本文通过在优化目标中将PCA与LLE的优化目标加权相加，使两种算法的优势互补.在MNIST手写数字图像数据集和ORL人脸图像数据集上的实验表明：融合PCA和LLE的算法PCA_LLE对数据降维，再用分类器分类，准确率有了一定程度的提高.