取整函数优化基于超结构模型的质量交换网络

侯 创，罗明生，徐文星

1.北京石油化工学院，北京 102617；2.北京化工大学，北京 100029

20 世纪末以来，随着清洁生产理念的提出、可持续发展战略的不断推进与环保对工业生产越来越严格的要求，企业逐渐考虑通过对资源的循环回用减少废物排放和新鲜物料的使用，达到环保和经济性目的。因此，作为过程系统工程中直接处理废物的有效工具，质量交换网络（Mass Exchange Network，MEN）综合得到极大地发展。

MEN 综合首先由El-HALWAGI 等[1-2]于1989 年提出，他们基于夹点技术提出夹点图法、浓度间隔表法和线性规划法确定MEN 的最小操作费用，接着以质量交换器数目最少为目标确定MEN 的结构；然而这种方法没有同时考虑操作费用和设备费用，并且质量交换器数目最少并不能保证网络的设备费用最小。后来，HALLALE 等[3-6]将目标设定为操作费用和设备费用的和最小，同时权衡了两种费用。

此外，随着计算机的发展，一些基于超结构的数学优化法的应用越来越广泛。从1994 年PAPALEXANDRI 等[7]提出基于超结构的混合整数非线性（MINLP）模型后，大量的科研人员开始进行该方面的研究；李绍军等[8]利用改进的遗传算法综合MEN；CHEN 等[9]提出用多级超结构建立数学模型；SZITKAI 等[10]建立了一个相当于线性的MINLP 模型；都健等[11-12]修改了MINLP 模型，得到了同步优化传质浓度差的非线性规划（NLP）模型，并用模拟退火遗传算法进行求解；ISAFIADE 等[13-14]组合了超结构和夹点技术的优点，通过增加约束缩小了超结构的解的空间，提高了求解效率，并且提出了一个两步的混合优化策略；LI 等[15]使用block superstructure 研究了过程集成技术；VELÁZQUEZ-GUEVARA 等[16-17]提出了基于state-task-network 的超结构模型。然而，上述这些方法，要么形成了较难求解的MINLP 模型，要么增加约束，减小了解的空间，很难得到真正意义的最优解，并且在他们的模型中，缺少对由于塔板数向上取整造成MEN 年度最小总费用偏大的讨论。本工作保证了在不增加其他变量和约束的前提下，用质量交换的存在与否判断质量交换器是否采用，除去MINLP 模型中的0～1 变量，将MINLP 模型简化为NLP 模型，并且在目标函数中加入取整函数，使求解结果更加精确，得到了一组一一对应的操作费用和设备投资费用，使年度总费用达到最低。

1 问题描述

其中：y和x分别为富、贫流股的污染物浓度；m和b的大小取决于贫富流股的性质；ε为贫富流股之间的浓度组成差，本工作中取常数。

本工作运用MEN 多级超结构模型（图1）建立NLP 模型。超结构的级数通常取贫、富流股中数目最大的个数。该模型包含了多种可供选择的结构性方案，形成了NLP 优化问题。该问题可以用LINGO 11.0 中的Global Solver 求解器求解，最后得到了年度总费用最低的MEN 结构。其中R1和R2表示富流股，S1和S2表示贫流股。

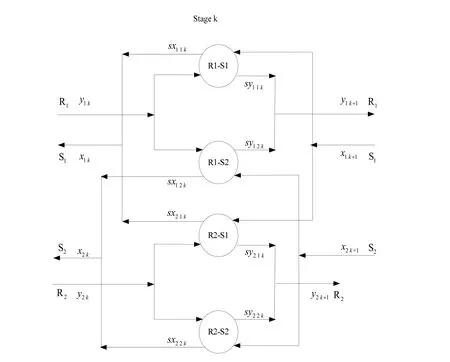
图1 分级超结构模型 Fig.1 Stage-wise superstructure

从图1 可以看出，贫富流股在质量交换器入口处分流，出口处混合，进出第k级超结构的贫富流股浓度分别为xj k+1，xj k，yi k和yi k+1进出第k级超结构内质量交换器的贫富流股的浓度分别为xj k+1，sxi j k，yi k和syi j k。

为了阐述在模型中对塔板数目取整的必要性，提出塔板数-费用图（图2）对该问题加以说明。图2 表示了一个质量交换器的塔板数与操作费用、理论投资费用、实际投资费用的关系，Z表示塔板整数，N表示理论塔板数。由图2 可以看出，理论投资费用与塔板数的关系是线性的，随着塔板数的增加，理论投资费用增大；实际投资费用与塔板数的关系则是一个分段函数，当塔板数不是整数时，实际投资费用对应的为塔板数向上取整后对应的费用值；操作费用与塔板数的关系则是非线性的，随着塔板数的增加，操作费用会下降。传统的优化模型认为：若理论塔板数取N时，操作费用和理论设备投资费用的总和最低，则此时输出的结果就是最优的设计方案；然而，实际的总费用应为操作费用和实际设备费用的总和，从图2 可以看出，当塔板数向上取整到实际数目Z+1 时，此时的操作费用应该更低，总费用才最小。举个例子说明：如果5.1 块塔板时，操作费用对应为20 000 元，而增加到5.9 块塔板时操作费用减少为18 000 元；如果前者的操作费用和理论投资费用和小于后者，则前者会被认为是模型的最优解。然而实际是，当两者的塔板数均被向上取整到6 时，塔板数为5.9时对应的总费用要低于塔板数为5.1 时的费用。为了解决这一问题，本工作在模型的目标函数中加入了对塔板数的取整函数，改变了目标函数的表达。用焦炉气的处理的案例对该模型进行验证，得到了相比较其他文献费用更低的质量交换网络。

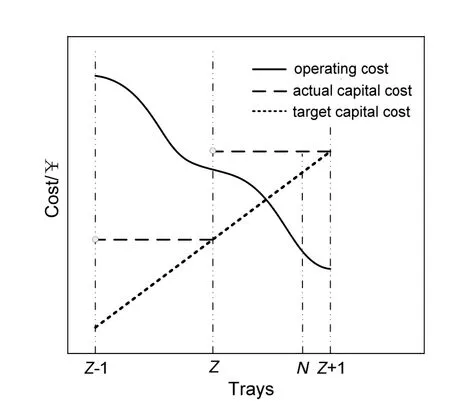
图2 塔板数-费用图 Fig.2 Trays-Cost diagram

2 多级超结构建立的NLP 数学模型

根据图1 所示的多级超结构，可以建立一个NLP 模型，该模型包括目标函数、质量守恒和可行性约束等部分。本工作在目标函数中加入了对板式塔塔板数的取整，并通过判断质量交换的存在与否来表达可行性约束，剔除了MINLP 模型中的0～1 变量，降低了求解难度。

2.1 目标函数

该NLP 模型的目标函数为MEN 的年度总费用（Total Annual Cost，fTAC）最低，它由外加质量交换剂的操作费用（f0）和质量交换单元的设备投资费用（fc）组成，表达式如式（2）所示。

若贫流股j的流量表示为Lj，单位流股的费用表示为Cj，则f0可用式（3）表示。

此外，本工作采用板式塔作为质量交换单元，其费用为单位塔板的费用（C′）和塔板数（Zi j k）的积。为了避免Kremser 方程中的不连续性，塔板数由公式（4）[18]计算。

其中：Δy和Δx分别为富、贫流股进出质量交换器前后的组成浓度差；Δy1为质量交换器富流股出口端与贫流股入口端的浓度差；Δy2为质量交换器富流股入口端与贫流股出口端的浓度差；取n值为1/3。

塔板数的求解结果需通过取整函数向上取整到最近的整数，如公式（5）所示。

公式（5）的LINGO 语言表达式为“Zi j k=@if（Ni j k#eq#@floor(Ni j k),Ni j k, @floor(Ni j k)+1”，其中，@floor为取整函数在LINGO 中的表达式。该语句可以解读为当Ni j k= @floor(Ni j k)时，Zi j k=Ni j k；否则，Zi j k= @floor(Ni j k)+1。最终，设备投资费用由式（6）表示。

2.2 约束条件

2.2.1 超结构总质量守恒

总质量守恒保证了从富流股中除去污染物的量，有足够的贫流股来接受，如式（7）和（8）所示。

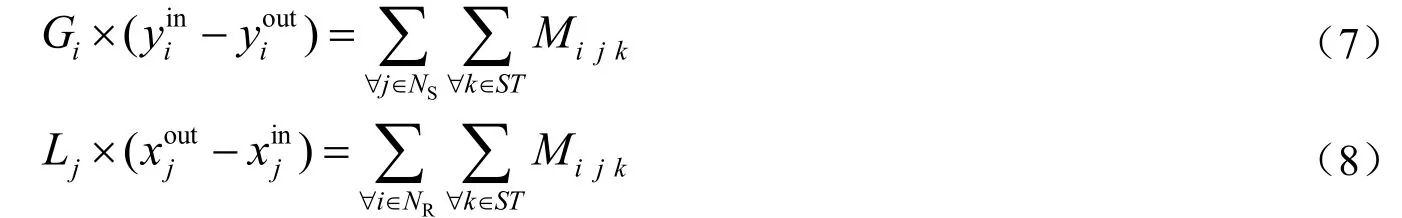
2.2.2 每一级的质量守恒

每一级质量守恒保证了该级内贫、富流股中污染物的质量交换是相等的，具体表达如式（9）～（12）所示。

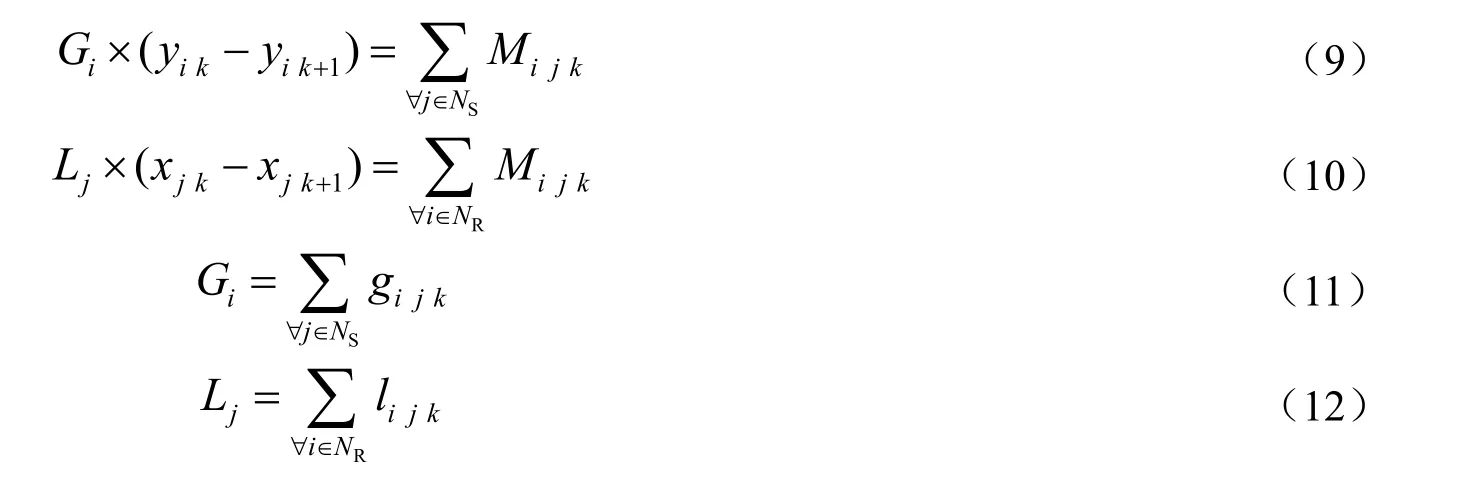
其中：公式（9）和（10）表示了第k级超结构内质量交换单元的质量交换量；公式（11）和（12）表示了在第k级超结构内，贫、富流股的流量守恒。

2.2.3 每一个质量交换单元的质量守恒

在每级的超结构中，贫、富流股通过每个质量交换器的流量li j k和gi j k，以及出口浓度sxi j k和syi j k均是未知的，这就构成了一组非线性方程，如式（13）和（14）所示。

2.2.4 质量交换的可行性约束

对于每一级的超结构，富流股的污染物浓度在质量交换后不断下降，而贫流股污染物浓度则不断升高，如方程（15）和（16）所示。

对于每个质量交换器，富流股的入口浓度高于出口浓度，贫流股的出口浓度高于入口浓度，具体表示如式（17）和（18）所示。

此外，在传统的MINLP 模型中，0～1 变量有两个作用[9]，一个是判断质量交换设备是否采用；另一个是表达可行性约束。为避免引入0～1 变量，都健等[11]通过进出质量交换单元的贫富流量大小判断设备是否被采用，增加了模型的连续性。然而，有流量通过，未必需要质量交换设备，若流股仅分流而没有质量交换，即便有流量通过，质量交换设备也不应存在。为解决上述问题，本工作通过判断质量交换的存在与否来表示可行性约束，即：当Mi j k为0 时，约束不存在；当Mi j k不为0 时，表达如式（19）所示。

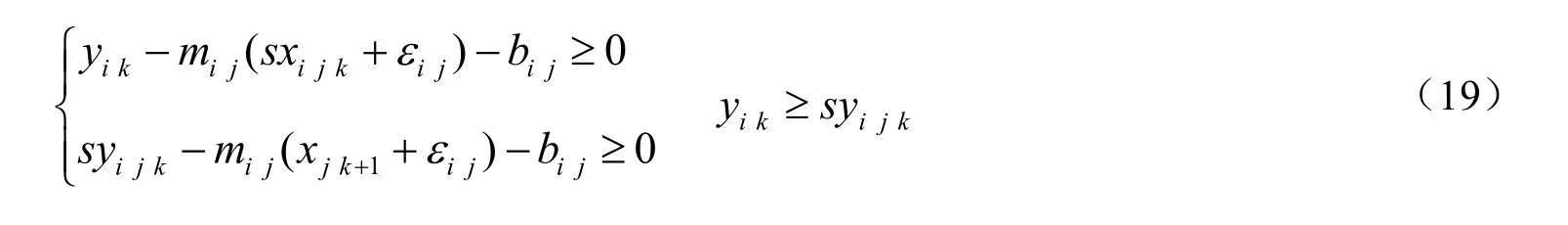
而质量交换设备是否被采用，则通过塔板数的结果是否为0 来判断。

通过使用该方法，剔除了CHEN 等[9]提出的基于超结构的数学模型中的0～1 变量，传统MINLP模型被简化为了NLP 模型，该模型更加容易求解。此外，由于该模型是通过质量交换设备的实际质量交换量来判断质量交换设备是否存在，因此该模型更加符合实际情况。由于所建立的模型为NLP数学模型，因此在求解时，选用建模求解软件LINGO 11.0 版本中的Global Solver 求解器，最终得到多级超结构模型的一组最优解，有效地解决了单组份MEN 综合问题。

3 案例研究：焦炉气的处理

该案例在1989 年被El-HALWAGI[1]用来阐述MEN 综合问题。焦炉气处理过程的目标是从两股废气（R1和R2）中除去H2S，在此过程中，有两种MSA：稀氨水（S1）和甲醇（S2），相关物流数据如表1 所示。

表1 案例的流股数据[9] Table 1 Stream data of this demonstration[9]

该案例给出H2S 在贫富流股中的传质平衡关系，如式（20）和（21）所示。

其中：ε1和ε2分别为贫、富流股间的传质推动力，为方便计算，在本例中均取0.000 1。此外，本例选用板式塔作为质量交换单元，单位塔板的费用为每年4 552 美元[7]。

该案例包含两个贫流股和两个富流股，因此选取两级超结构；由方程（2）～（19）建立NLP 模型，该模型包含了66 个变量和100 个约束条件，其中非线性约束为52 个。运用LINGO 11.0 中的Global Solver 求解器求解，得到了如图3 所示的MEN 结构。

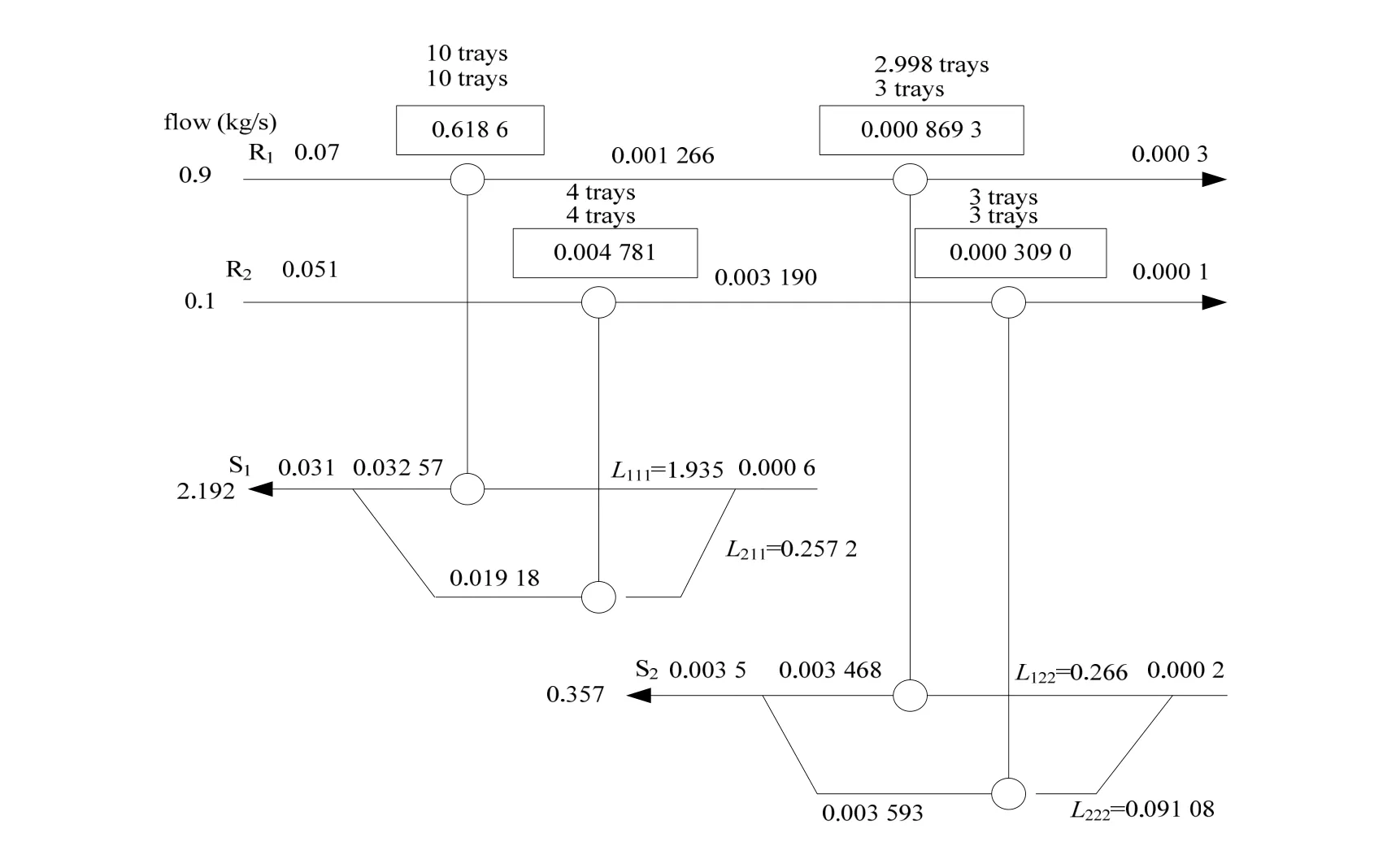
图3 案例的MEN 最优结构 Fig.3 The MEN optimal structure of this case

图3 包括了贫、富流股组合的情况、详细的物流分割数据、污染组分浓度的变化以及质量交换单元的塔板数。该结构与CHEN 等[9,11]等得到的MEN 结构相同，如图4 和5 所示。但总的年投资费用较文献值有所下降，具体的结果对比见表2。

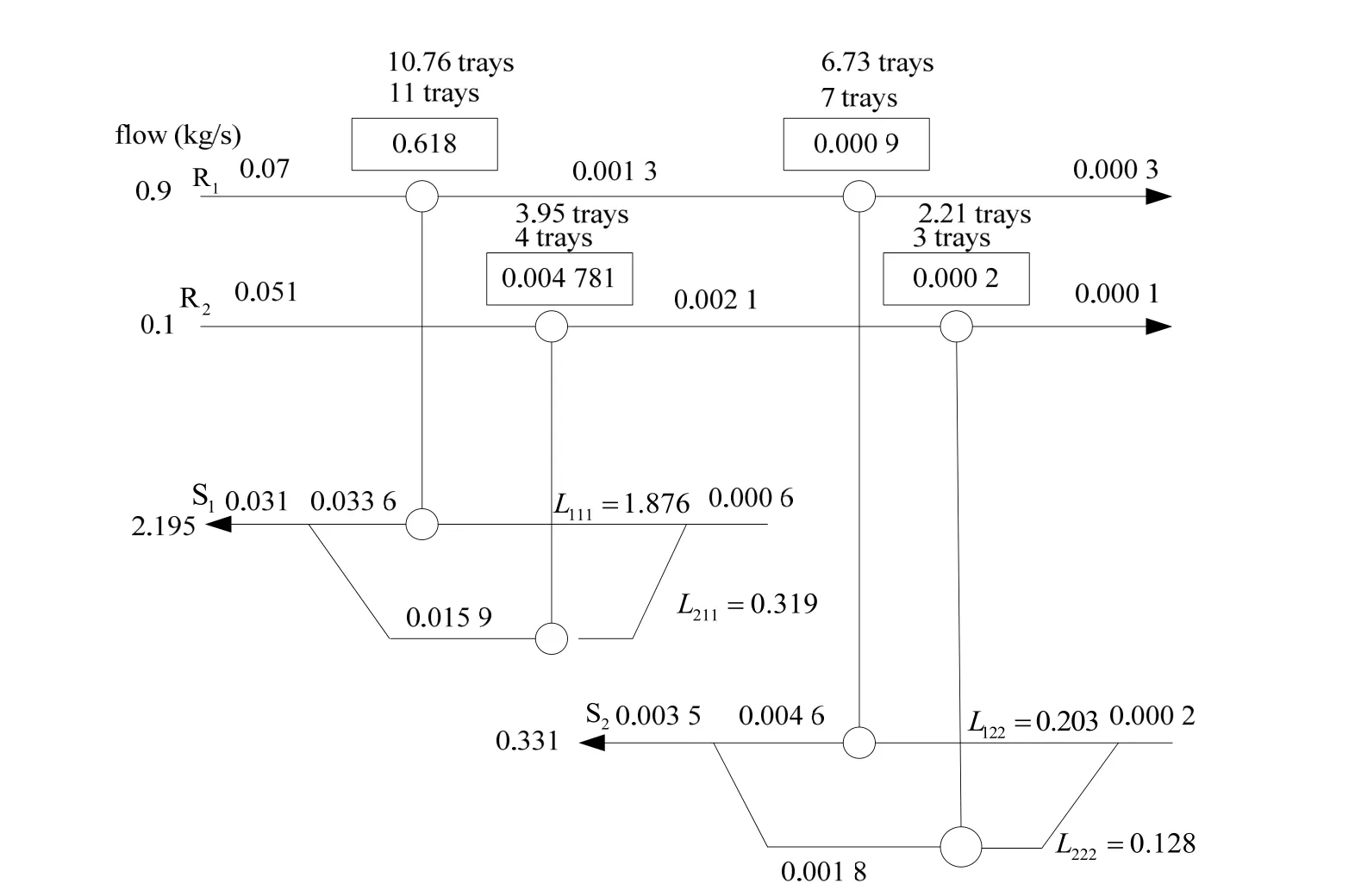
图4 文献[9]报道的MEN 最优结构 Fig.4 The MEN structure reported in reference [9]

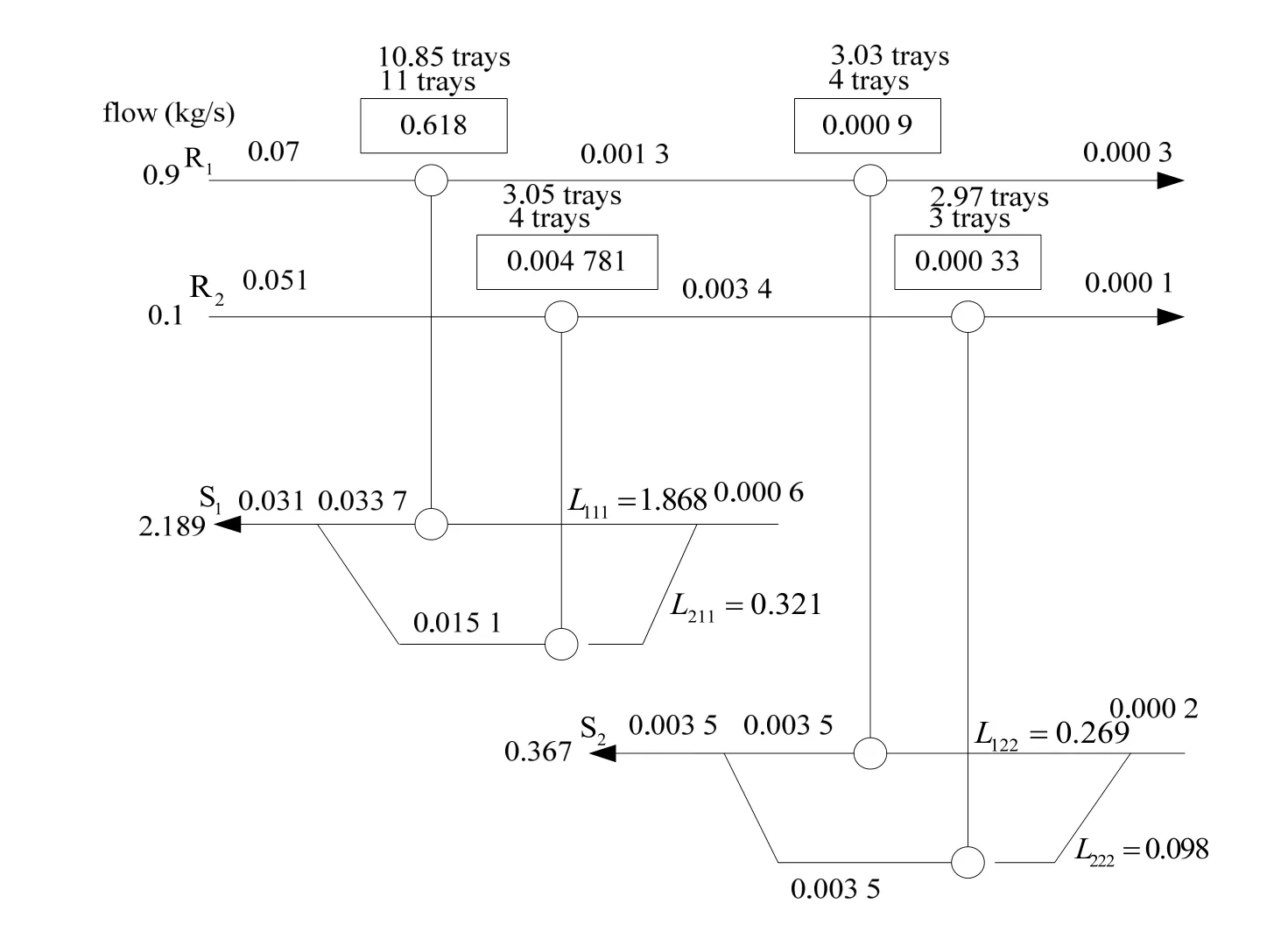
图5 文献[11]报道的MEN 最优结构 Fig.5 The MEN structure reported in reference [11]

表2 案例的结果对比 Table 2 Comparison of results based on the different model

由表2 的对比可以看出，本工作的MEN 结果的总费用为411 166 美元，比传统MINLP 模型的总费用下降了约4.3%；在没有优化传质浓度差的情况下，该NLP 模型的结果比优化了传质浓度差的文献[11]的结果下降了2.5%。相比较于传统的MINLP 模型，该模型总的塔板数从25 下降至20，在图3～5的MEN 结构图中显示了理论塔板数和实际塔板数的对比情况（其中理论塔板数为上方的小数值，实际塔板数为下方的整数值），如果将理论塔板数和实际塔板数的比值定义为塔板的利用率，则图3 中每个质量交换器中每块塔板的利用率是最高的，单块塔板利用率提高，因此总的塔板数目有所减少。得到这一结果的原因是：本工作在数学模型中加入了取整函数，并且利用取整后结果计算设备投资费用，结合图2，当理论塔板数越接近整数，则对应的操作费用越低，因此得到的所有理论塔板数均非常接近整数值。从该模型的结果看，由于塔板数的减少，设备投资费用下降，且下降幅度大于操作费用增加的值，因此，用该模型可以得到费用更低的MEN 结构。

为了更好地显示出取整函数的作用，本工作去掉了数学模型中的取整函数，得到了一组新的结论，该结论与包含取整函数的结论对比结果见表3。从表3 可看出，加入取整函数后，塔板数略微下降，这是因为取整函数使每块塔板的利用效率充分提高，因此总的塔板数目有所下降；此外，操作费用略微升高，但其升高的量小于设备投资费用的减少量。这组对比直接表明了使用取整函数能够得到费用更低的MEN 结构。

表3 是否加入取整函数的结论对比 Table 3 Comparison of the NLP model results with or without integral function

4 结 论

针对单组份MEN 综合问题，通过在原有数学模型的目标函数中加入取整函数，解决了由于塔板数取整造成的最优MEN 结构中的理论塔板数和实际塔板数存在的差异问题。将年度总费用最低作为目标函数，将总质量衡算、每级质量衡算、各质量交换单元的质量衡算、可行性限制以及环境限制作为约束条件，建立了以多级超结构为基础的NLP 模型。在该模型的目标函数中加入取整函数后，每块板式塔塔板的利用率得到了提高；此外，该模型通过判断质量交换单元的质量交换是否存在来表达交换单元两端的热力学约束，避免引入0～1 变量，简化了传统的MINLP 模型；该模型用LINGO 的Global Solver 求解器求解，得到了费用最低的MEN 结构。对焦炉气的处理案例进行计算结果表明，该NLP 模型可以得到较文献更优的MEN 结构。因此，该模型可以用来处理基于多级超结构的单组份MEN 综合问题。另外，这种改变可以加入到其他的质量交换网络综合的方法中来改善模型，这将给设计者提供一个更加准确和费用更低的设计方案。