基于嵌入式零树编码算法的图像压缩技术

2020-02-07荀燕琴任国凤田竹梅吴莹莹

渭南师范学院学报 2020年2期

荀燕琴，任国凤，田竹梅，吴莹莹

(忻州师范学院电子系，山西忻州 035000)

信息时代，图像是获取信息的一个重要途径。随着数码电子产品的快速发展，人们对日常生活中各种数字图像的清晰度要求越来越高，给人们的生活带来了许多的乐趣，但同时也会有一些问题出现。数字图像的数据量很大，而现如今的硬件技术所能提供的存储空间有限，这给多媒体的存储和传输带来了很大的压力。尽管存储硬件的容量不断增加，传输器的速度也不断发展，但信息数据量是爆炸式增长的，仅仅依靠增加硬件的存储能力或是增加带宽并不能从根本上解决问题，它永远也跟不上信息的增长速度。因此，为了最大程度地解决问题，需要对图像的数据信息进行压缩。[1]

本文基于图像的压缩背景、研究现状及压缩理论，描述了图像压缩算法的评价指标及相关算法，详细分析了小波变换原理、典型算法及应用。在此基础上研究了嵌入式小波零树编码算法的基本理论和算法的实现过程，并通过MATLAB进行图例仿真及数据分析。

1 图像压缩性能评价

1.1 压缩图像性能评价方法

1.1.1 主观评价方法

对于图像的好坏，首先是从人的视觉来感知的，图像的质量若按5分制[2]来评分，具体情况如表1所示。

表1 图像主观性能评价表

1.1.2 客观评价方法

一般来说，常见的客观评价方法[3]有以下几种：

均方误差的计算方法见式(1)

(1)

信噪比的计算方法见式(2)

(2)

峰值信噪比的计算方法见式(3)

(3)

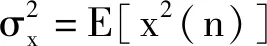
1.2 图像压缩编码方法

图像编码的主要目的是完成图像的压缩，使储存和传输更加方便。图像压缩编码可分为无损编码和有损编码。

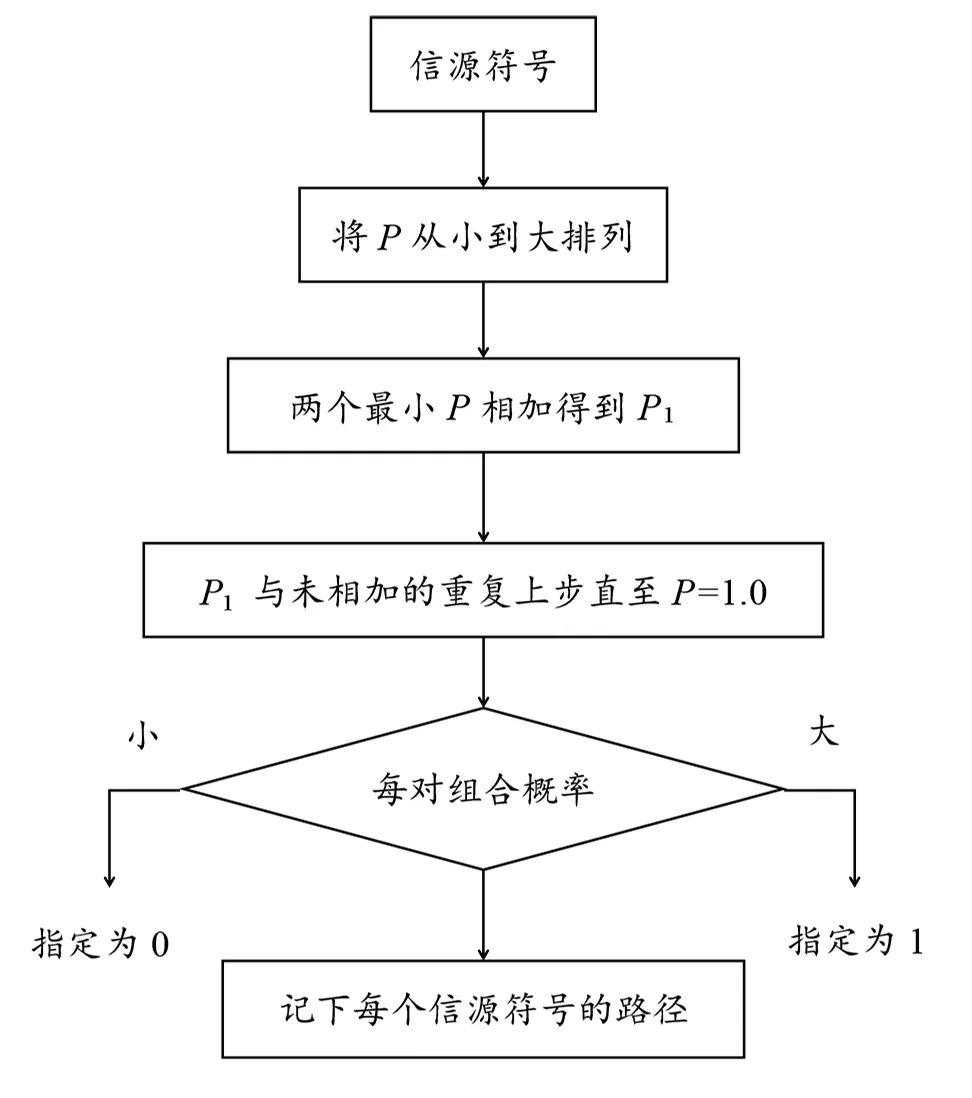
图1 哈夫曼的编码步骤

1.2.1 无损编码

(1)哈夫曼编码

哈夫曼编码是一种常用的编码算法。它的特点是简单、高效且长度不同。若它的码子长度和符号概率大小的摆列是逆序排列，则其平均码长就是最短的，被称作最佳码。

该编码算法的编码流程如图1所示(设概率为P)。

(2)算数编码

20世纪80年代出现的算数编码是一种能够逼近熵极限的最优编码算法。它和哈夫曼编码不一样，哈夫曼编码不能用小数表示信源符号，但算数编码可以。将需要编码的符号流看作一个范围在[0,1)上的实数区间，区间会随着信源符号逐渐进入信源流中而减小，新进入的信源信号的先验概率越大，区间减少就越慢。符号流越长代表区间越短，编码所需的比特数也会随之增多。因此，算数编码会得到一个数a(0≤a<1),在解码时能进行准确的重构。

在信源概率散布均匀的情况下，相对于哈夫曼编码来说，算数编码的效率更高，也不需要对数据进行分块。

1.2.2 有损编码

(1)变换编码

变换编码就是为了压缩数据而对正交交换后的数据进行编码的一种方法。[4]不管图像是不是彩色的,也不管是不是动态图，都可用变换编码。变换编码的模型如图2所示。

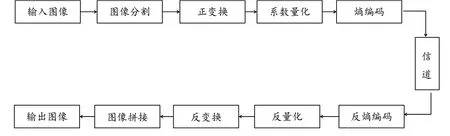
图2 变换编码的基本流程

(2)小波变换编码

近年来，小波变换被广泛地运用在图像编码、语音处理等领域。它对图像信息进行处理时，能够精细地对高频成分进行取样，从而可以对图像任意局部进行分析。

2 小波分析

2.1 小波分析概述

小波分析最早由法国的数学家提出，20世纪30年代到80年代间出现了小波分析思想。法国物理学家Jean Morlet通过对Fourier变换和短时Fourier变换的研究，给出了小波分析的概念，后来经过无数人的研究出现了多分辨分析的基本理念。在该理念的基础上，Mallat给出了著名的Mallat算法，推动小波变换逐渐运用到现实中。

通过小波变换可对时频域进行局部分析，经过伸缩平移不断变化多尺度细化信号，最后可对低频处的频率进行细化，可对信号的任意细节进行处理。因为小波变换具有这些优点，所以它能被应用于图像压缩等多媒体领域中。

2.2 小波分析原理

2.2.1 小波及小波变换

小波就是表示小范围的波。

小波函数[5]是指函数φ(x)在空间L2(R)中满足公式(4)：

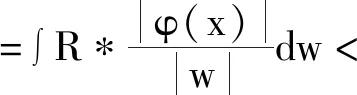
(4)

将小波母函数φ(x)伸缩和平移，假设其尺度因子为α，平移因子为τ，令其伸缩平移后的小波基函数为φα,τ(t)见式(5)

(5)

其中：α和τ是小波基的两个重要系数，φ(x)具有振荡和衰减的性质。

小波连续变换就是在任意空间L2(R)中，在小波基下展开后的函数f(t)，小波变换系数的表达式见式(6)

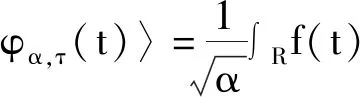
(6)

2.2.2 小波基的选取

图像经小波分解后的总能量不会减少，但图像的能量会重新分布，能量主要聚集到低频部分。阳婷等[6]提出图像两层小波分解：其中LL2是最低频也是最重要的，最低频的小波系数有3个子孙系数，除最低频以外的小波系数有4个子孙系数外，最高频没有子孙系数。两层小波分解如图3所示。

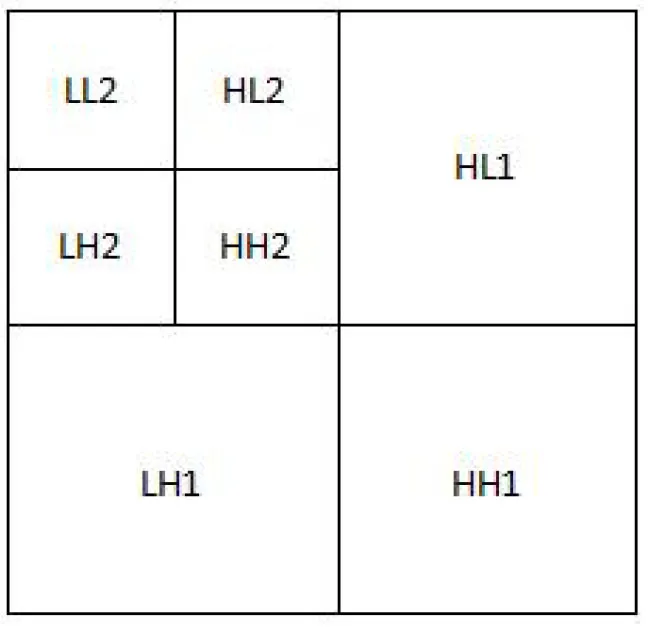
图3经小波分解的图像示意图

尽管图像经小波变换得到了新的小波图像，但是和原始图像的数据量是相同的。由此可知：通过小波变换不能实现对图像的压缩，还需再经过其他的方法才能对图像进行压缩。但是在图像压缩中依然使用小波变换的原因是因为变换后生成的小波图像的特征和原始图像不同，虽然变换后的总能量没有发生变化，但能量分布发生了变化。变换后的图像能量主要集中在低频部分。

在基于小波变换的图像编码压缩方法中，对小波基的选取非常重要。小波基[7]须具有如下的一些特征：

(1)正交性

经小波变换处理的图像会分解成携带数据的一些子带，正交性会使这些数据落入互相正交的子空间中。这样，会减少各子带数据间的相关性。

(2)对称性

在图像压缩中，尺度函数和小波函数的对称或反对称是十分重要的，因为它可构建出紧支的正则小波基，且它的相位具有线性特征。

(3)正则性和消失距

消失距可以表示小波变换后的能量集中程度。消失距越大，图像经过小波分解后的能量越集中，则它的压缩比就越有可能被提高。

3 基于嵌入式零树小波编码的图像压缩

嵌入式零树小波编码算法[8]是一种高效的小波图像压缩算法,是指基于图像小波变换的数学结构，EZW是采用Z字形扫描，由零树结构结合逐次量化逼近来实现的。

3.1 嵌入式零树小波编码算法基本原理

3.1.1 嵌入式编码

在码流的开始部分插入一个低比特的码流，把包括这段低码流的码流段截取出来后得到一段不缺失的更低码率的码流，这段码流可参与重构图像。嵌入式编码就是指编码器输送出的码流有以上的特征。

3.1.2 零树

零树结构就是指图像经过小波变换后，分解成为不同尺度的一系列子图。根据阈值找到小于阈值的小波系数，若与其有关的子孙小波系数也小于阈值，则这些系数就可以构成零树。构建示意图如图4所示。

图4零树构建示意图

小波变换编码中，根据给定的阈值T，若当前小波系数绝对值大于给定的阈值T，此小波系数就为重要系数。小波系数一般可以分成4类：

(1)ZTR：当前小波系数是重要系数，子孙后代无重要系数。

(2)IZ：当前小波系数是重要系数，子孙后代有重要系数。

(3)POS：当前小波系数是正重要系数。

(4)NEG：当前小波系数是负重要系数。

3.1.3 Z字形扫描

零树扫描根据人眼视觉的特性，以从上到下、从左到右的顺序按低频率到高频率进行扫描。具体Z字形扫描如图5所示。

3.2 EZW算法流程

EZW算法主要包括以下3个重要的步骤：零树预测、用零树结构编码重要图以及逐次逼近量化。

3.2.1 零树预测

迟洋[9]提出零树预测的概念：若一个小波系数X不重要，在更高频率上相应位置的小波系数也不重要，那么这些小波系数就会参与构成一棵零树。由于这种零树结构的存在，其子孙系数就不用参与编码，位置信息就会大幅度减少，在一定程度上就可完成对数据的压缩。

图5 EZW的Z字形扫描顺序

3.2.2 用零树结构编码重要图

首先确定初始T,然后经过Z字形扫描来构成零树。利用上述提到的4种符号(ZTR、IZ、POS和NEG)按Z字形顺序扫描小波系数形成有效值映射。具体流程图如图6所示。

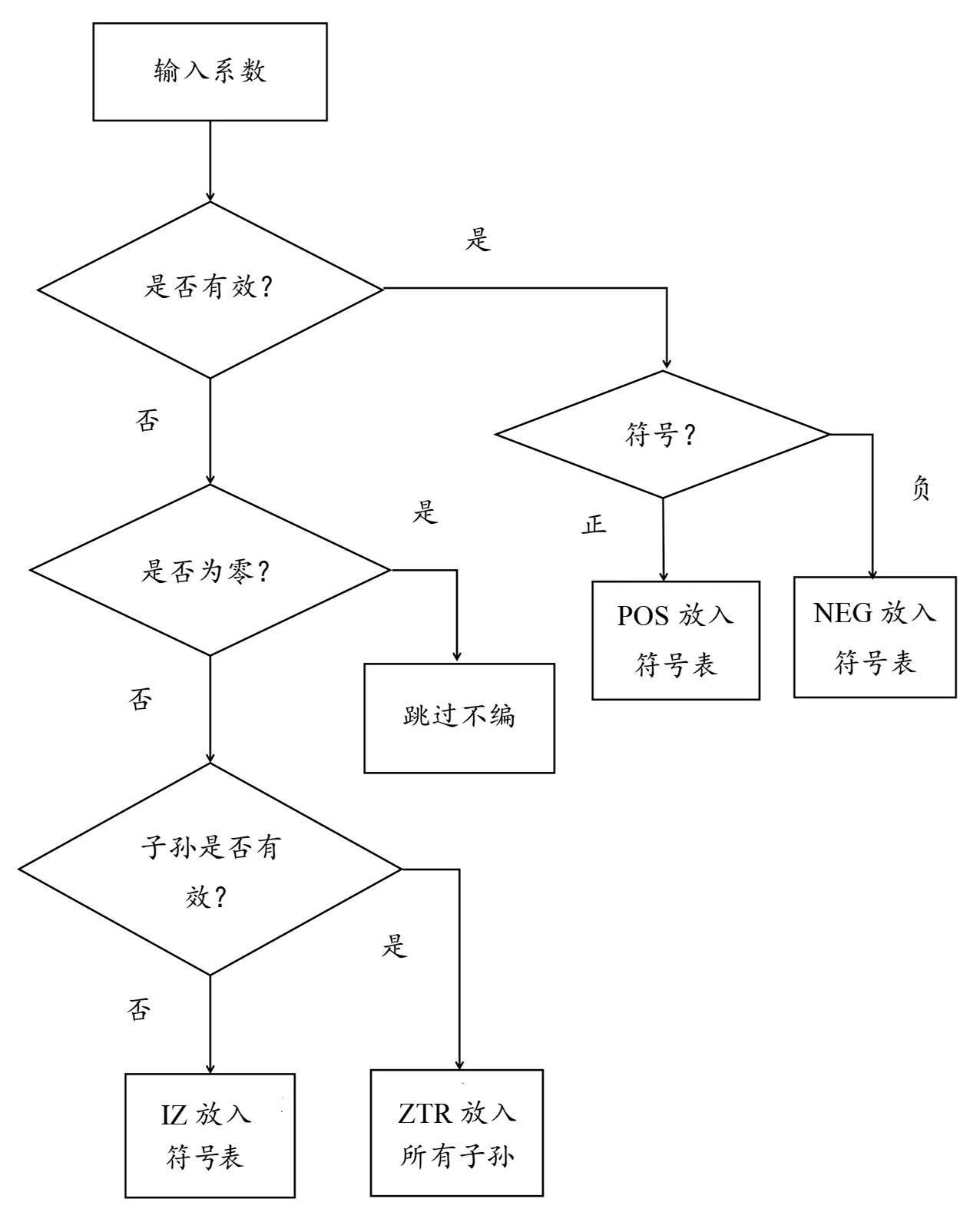
图6 有效值流程图

3.2.3 逐次量化编码

刘忠元[10]对逐次量化编码进行了介绍：初始阈值T0要满足|Xmax|<2T0,Xmax是小波变换系数矩阵的最大绝对值，阈值序列的选取是按照Ti=Ti-1/2来选取的。SAQ和零树结构结合后，其工作方法为：先确定T，进行第一遍主扫描，进而形成主表；再进行副扫描，细化有效值。按照阈值选取公式确定新的阈值，再进行主扫描，这时已是有效值的位置无须再扫描，为了方便发现零树只要将它们设为0；再进入新一轮的副扫描，细化之前发现的所有有效值。然后一直按这种方法进行处理，直至达到要求。

EZW编码算法流程图如图7所示。

图7 EZW编码算法流程

3.3 基于嵌入式零树小波编码的图像压缩实验仿真

实验在MATLAB 7.0的操作环境中进行仿真。

对标准测试lena图像进行基于小波变换的图像压缩，根据阈值不同所得数据及选取的仿真图像分别如表2及图8所示。

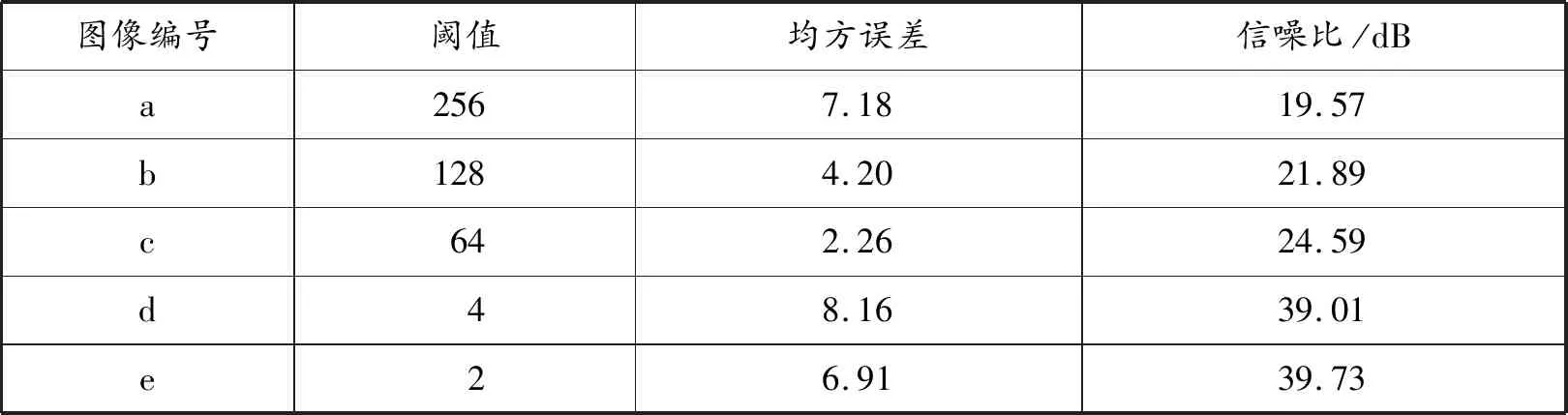
表2 仿真所得部分数据

由图像质量评价方法知道，对于图像压缩有主观评价方法和客观评价方法两种。

按照主观评价方法，可以直观地去观察图像，通过人眼的观看去判断图像质量的好坏。通过对EZW算法进行仿真所得的图像来看：图8(d)视觉效果明显比图8(a)的视觉效果要好，图8(a)的许多细节非常模糊，不便于人眼的观看；而图8(d)的呈现就非常清晰，对于人眼视觉的观看几乎没有影响。同样，图8(e)相对于图8(b)来说，阈值在减少的同时人眼观看效果也更好。

按照客观评价方法，MSE和PSNR是图像重要的评价参数。但由于均方误差的计算公式相对简单，所以依靠均方误差的评价结果并不可靠。由表2中所得仿真数据结果分析得出：随着阈值的减小，均方误差的变化没有什么规律，不能作为图像质量的评价依据。而PSNR是最广泛使用的评价画质的客观测量法，PSNR值越大表示图像失真越小。由表2明显可以看出，图8(e)的PSNR比图8(c)的PSNR大，说明图8(e)的画质更好，由仿真所得的图像也可以直观地感受到图8(e)的图像质量更好。图8(d)相对于图8(a)也是这样，在表2中的PSNR更大，在仿真图像中的质量也更好。