环境污染下具有密度制约的两种群竞争模型稳定性分析
2020-02-07杨秀香
杨 秀 香
(渭南师范学院 数学与统计学院,陕西 渭南 714099)
0 引言
生活在一个自然环境中的两种生物x和y,由于在生态系统中的生态位重叠发生争夺生态资源而进行斗争的现象即为两种群的竞争。设x(t)、y(t)表示两个种群在t时刻的数量,假设两种群在独立生存条件下其增长方式符合Logistic方式增长,则Lotka-Volteera竞争模型为
其中:β11、β12、β21、β22为非负常数,模型表明了x和y种群是密度制约的,且两种群是相互竞争的。
随着科技的发展,环境污染日益严重,大量的有害物质排放到自然环境中,对生物体的生长发育和繁殖等都有着较明显的影响。目前研究环境污染影响生物种群发展规律的成果已有很多:文献[1]是环境污染与自然资源耦合系统的动力学模型性分析;文献[2-6]通过数学模型研究环境污染对人类的危害;具有环境污染的两种群互惠模型的稳定性分析;生态环境受污染的单种群持续生存的研究;大气污染下具有HollingⅡ功能性反应的种群生存条件。
本文在文献[3]的基础上研究一类具有环境污染的两种群竞争模型,假设种群的密度制约均匀,结合生物动力学原理和生态毒理学原理,建立具有密度制约和毒物影响、一种群具有阶段结构、成年才具有竞争能力的模型:
(1)
其中:d1、d3分别表示x种群、y种群的自然增长率,d2表示x种群由幼年转化为成年的转化率;m1、m2、m3分别表示x种群的两个阶段以及y种群的密度制约系数;α、β表示两种群竞争关系中相互间的干扰系数,y种群只捕获成年的x种群,只有成年的x种群才捕获y种群;c1、c2、c3分别表示x种群不同阶段以及y种群受毒物影响的消耗率;r1、r2、r3分别表示x种群不同阶段以及y种群的自然死亡率。这些系数均为正常数,基于实际意义,d1>c1,d2>c2,d3>c3,否则两种群受环境污染下负增长而消亡。我们在R={(x,y)|x≥0,y≥0}内讨论模型(1)的稳定性态。该模型的一切解在R内正向有界。记n1=r1+c1+d2;n2=r2+c2;n3=d3-r3-c3,模型变为
(2)
1 定义与引理
定义1 方程组
X′=f(t,X),G={(t,X)|t≥T,X∈D⊂Rn},
(3)

引理1 赫尔维兹判别方法:设一元常系数n次代数方程
a0λn+a1λn-1+a2λn-2+…+an-1λ+an=0,
(4)
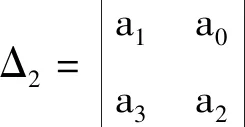

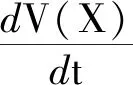
2 模型正平衡点分析
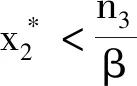
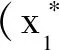
(5)
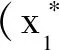

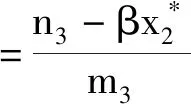
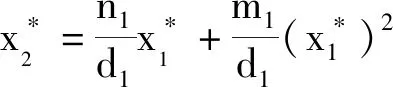
(1)当m2m3-αβ<0,K1>K2时,L1,L2在第一象限有唯一的交点。
(2)当m2m3-αβ>0,K1 (3)m2m3-αβ=0,n2m3-αn3>0,L1,L2在第一象限有唯一的交点。 (6) 系统(6)在平衡点(0,0,0)处的雅克比行列式为 系统(6)的特征方程为λ3+a1λ2+a2λ+a3=0。 其中:a1=H1+H2+H3, λ1,λ2,λ3具有负实部,由引理1(赫尔维兹(Hurwitz))必须有a1>0,a2>0,a1a2>a3,此时 证明 构造李雅普诺夫函数 其中:ω1、ω2为正常数,V沿模型(6)的导数为 (7) 代入 V函数(7)变为3 模型正平衡点的局部渐近稳定性
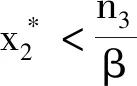

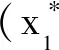
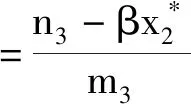




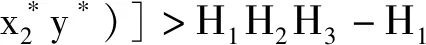
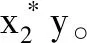

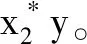
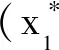
4 模型正平衡点的全局稳定性分析
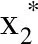
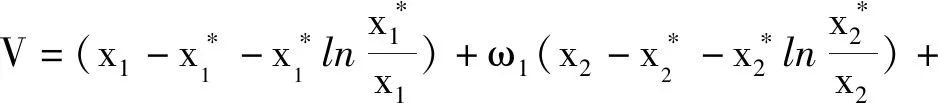
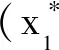
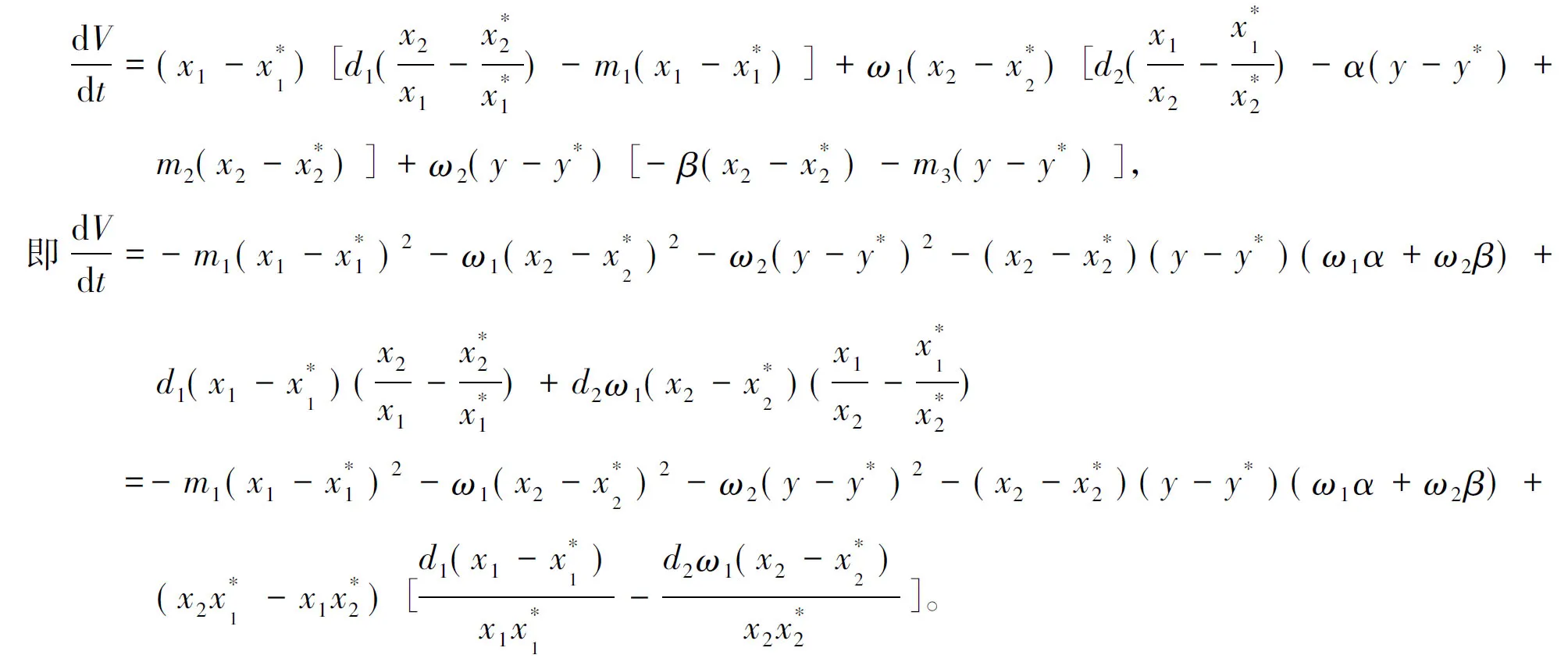
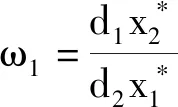
5 生物学解释