以几何学习入门困境为起点，整体设计几何入门教学

赵毅

【内容摘要】华东师范大学崔允漷教授认为学科核心素养：是指学生经过学科学习后形成的关键能力、必备品格和价值观念，能实现知识与技能、过程与方法、情感态度价值观“三维目标”。几何学作为数学领域的一个重要分支，在认识现实世界，培养逻辑推理能力、空间想象力培养学生数学学科核心素养方面发挥着不可忽视的作用。但对于几何教学，教师教的感受、学生学的感受都是：几何入门难。

【关键词】几何 入门困境 入门教学

针对几何入门难的相关研究很多，总结归纳发现，学生学习感到困难的三个方面为：空间观念，推理论证，语言表述。并且学生对数学问题解决的意识淡薄，具体到几何问题的解决过程中又主要表现为：一是阅读和书写困难;二是逻辑推理方面的障碍;三是思维不活跃，易受已有解题模式的禁锢，解题缺乏变通性。

一、几何入门难成因分析和整体教学建议

1.从初中几何的内容和要求等方面进行分析

第一，从学习内容上看，一是平面几何的研究对象从数到形，研究方法也从“运算为主”转到“推理为主”，另一方面，几何学习初期新概念大量集中出现，几何概念学习方式，以及对概念习得的检验途径与以往也存在很大不同，所以无论是在知识的学习、技能和能力的形成，还是在学习方法和学习习惯等方面，学生必将存在着不适应的情况;第二，从学习者能力要求和发展规律看，进入初中后，学生的思维水平正处在从形象思维到抽象思维的过渡时期;学习内容定位上是从实验几何到论证几何，学生前边学习实验几何时，学生经历的是合情推理，而后面要学习的论证几何学生要经历的是演绎推理。因此，这正是一个从形象思维思维到抽象思维、从合情推理到演绎推理的过渡关键期。

2.几何入门教学建议

几何入门教学要解决文字语言、符号语言、图形语言的相互转化;从训练思维灵活性角度入手，强调一题多解、一题多变，倡导思维的开放性;从训练思维的灵活性入手，建议提炼典型图式，在读题审题环节中重视挖掘典型图式，以便于最快速的方式找到解题思路;还比如从逻辑训练的严谨性入手，建议使用波利亚《怎样解题》的思路，制定解题计划，进行解题过程反思，逐步提升学生的元认知能力的培养。应该说以上建议，从不同的角度提出了对于几何教学的实施建议，各个建议都具备很强的操作性，有很强的指导价值。

综上我们认为几何入门：一是梳理几何学习的基本框架，建构几何学习的知识网络;二是建议梳理几何证明的思考框架;三是以学习者为中心开展几何入门教学。

二、教师要建构适应学生学习特征的结构化教学策略

几何的学习方式与代数学习不同，从学习要求上看，抽象概念理解的内容会增多。由此在教学策略中，教师应有意识的根据不同的研究对象，基于不同的学习策略，在几何学习中更应该看中学习方法的迁移策略。

1.聚焦研究策略及其迁移

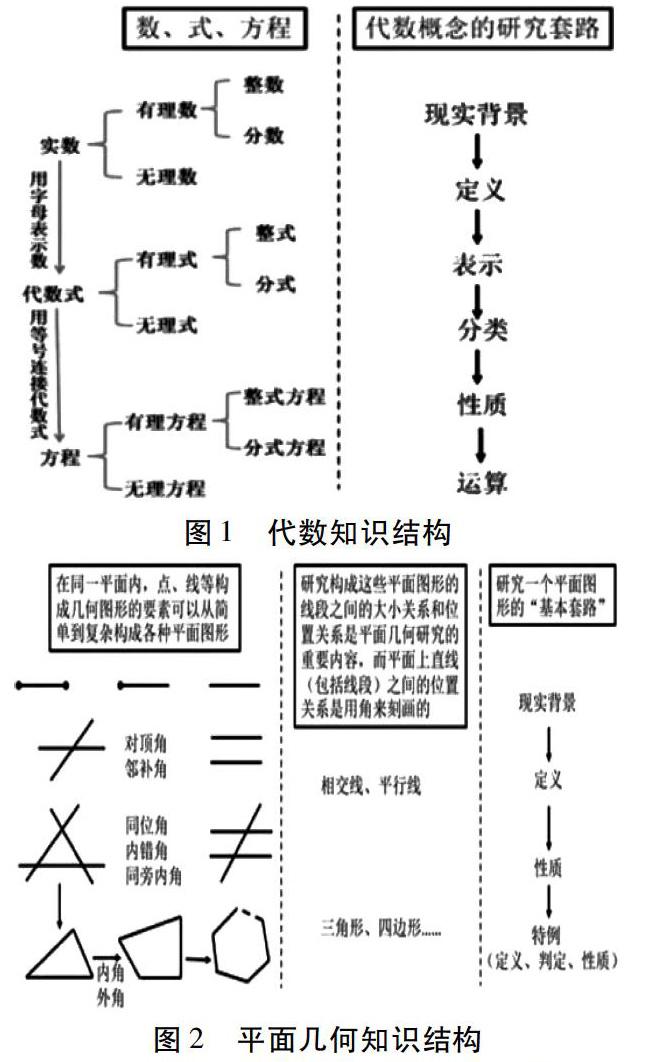
教师要从“研究一个数学对象”的角度思考和设计教学过程，在研究对象的抽象、研究内容的确定、研究思路的构建、研究方法的引导等方面整体规划教学思路，帮助学生迁移相似问题研究策略。圖1、图2分别给出了代数概念和平面图形的研究策略。教师在讲授每一个代数概念或平面图形时，应反复强调这种研究套路，以便学生逐步掌握这种研究数学对象的“大观念”。

2.重视整体教学

几何学习首先看重知识之间的关联，引导学生完成知识之间的整合。这种整合首先是建立在知识之间的有机链接，如与小学所学图形之间的关联，本章所学内容之间的关联，章节与章节间知识的关联。通过知识的结构化、模块化和网络化，丰富学生的认知结构，从而进一步加深结构化学习的体验，引导学生通过知识的网络化呈现知识体系之间的逻辑联系，形成系统理论，为几何证明奠定知识基础。

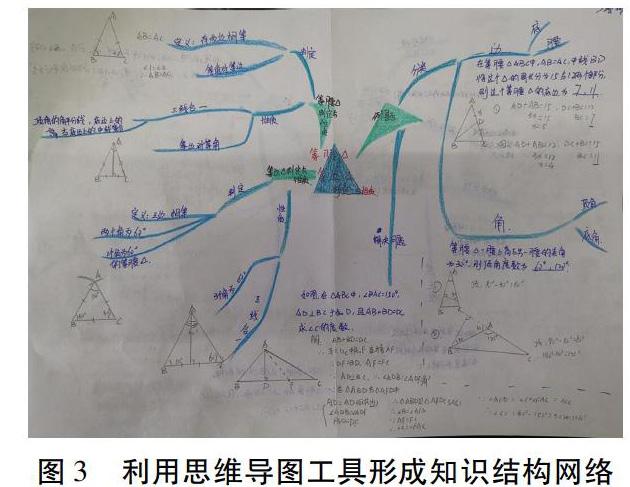
一是要重视课本“章头图”教学，章头图教学能够帮助学生构建良好的数学认知结构、掌握基本思想方法、感受数学应用的广泛性。二是要重视课本章后“小结”教学，利用“小结”，加深对数学知识的理解;梳理知识结构;提炼数学思想方法。而对于结构的重现可以在学生喜欢的直观性理解工具“思维导图”中呈现，在导图中反映知识间关系，罗列典型的几何问题，在典型问题中抓取“几何图式”，从而让几何问题和图式间建立强相关的逻辑联系，如图3。

三、紧抓“会说、会画、会书写、会证明”学习目标，引导学生推理论证能力形成

初中平面几何遇到的困难有：一是不会用几何语言表达 （有口难言）;二是不会用尺规作图工具进行尺规作图 （有手难画）;三是不会按逻辑顺序书写证明 （有笔难写）：四是不会寻找解题思路，探索解题途径 （有路难寻）。

1.将三大能力的培养作为几何学习的基础

一是“翻译能力”培养。图形、文字和符号是几何学习中的三大语言，要学好几何，三大语言之间的“翻译能力”是基础。培养翻译能力首先是要让学生养成联系图形据理叙述的习惯。定义、定理、公理是几何的根本，证明中要将文字、图形和符号进行翻译，如图4。

二是识图能力培养。识别规范图形、善于分解复杂图形，才能完成几何的推理和判断。几何证明的正确判断与推理往往是以正确的识图为先到的，学生不仅要学会看规范易懂的图形，还要善于观察复杂图形中的基本图形，会把复杂图形简单化。如教学线段、角的概念时，应让学生有条不紊地说下图（1）中有几条线段？图（2）中有几个角？再让学生观察图（3）中LAOC与LBOD 的关系，并练习：如果∠AOB=∠COD，那么∠AOC=∠BOD。这样，在三角形全等的证明中，学生就容易识别图（4）， （5），从而较快地得到证明AC=BD的方法。

三是思维能力培养。逻辑证明可以划分为综合法和分析法。循序渐进是几何学习的基本原则，在寻找解题途径时先熟练掌握综合法：由因索果，在此基础上再来联系分析法：探索已知与未知之间的“桥梁”，从不同方向和角度思考，由果索因，善于反思总结，提高分析和解决问题能力。