小学数学总复习之运算能力再提升策略研究
2020-01-18王琛
王琛
摘 要:文章从“估算能力的再培养”“简算能力的再提升”和“解方程的再思考”等三个方面展开小学数学总复习之运算能力再提升策略研究。经过加强估算能力的培养、提高简算的敏感度、灵活选择策略进行计算的训练,在总复习阶段绝大多数学生的运算能力一定能得到再提升。
關键词:小学数学;运算能力;策略
很多小数教师认为一二年级的数学教学在于习惯的养成,三四年级的数学教学在于培养计算能力,五六年级的数学教学在于培养学生解决实际问题的能力,因此在五六年级,特别是六年级往往侧重知识传授,而忽视了运算能力的培养。《义务教育教科书教师教学用书》中指出:“进一步理解和掌握四则运算的意义和方法,四则混合运算的运算顺序,以及加法和乘法的运算律,知道减法和除法的有关性质,能灵活地进行有关的计算,能运用学过的计算解决一些实际问题。”特别是在“数学思考能力培养”中重点关注的五种能力的第一项能力就是运算能力。值得一提的是,经过对美国数学教师协会(NCTM)出版的学校数学课程标准的研究,笔者发现在美国等发达国家,一样非常重视运算能力的培养。那么如何在总复习时提升学生的运算能力呢?本文从“估算能力的再培养”“简算能力的再提升”和“解方程的再思考”等三个方面展开小学数学总复习之运算能力再提升策略研究。
■一、估算能力的再培养
培养学生的估算能力,最重要的就是让学生在联系生活解决问题时逐步感悟估算的必要性,在具体实践中体会到估算的作用,从愿意估算到乐于估算,形成自觉估算的意识。当然,对运算结果估计的感悟,也有助于培养学生的数感。笔者将从先估后算、先算后估和估算的技巧三个方面进行阐述。
1. 先估后算,把握范围
在苏教版小学数学的总复习中有这样一道题目:“华光电影院楼下有698个座位,楼上有219个座位。这个电影院能同时容纳1000人看电影吗?”像这样的题目,笔者认为可以采取先估算再精算的策略,698可以看作700,219可以看作300,700+300=1000;因为698<700,219<300,两个估计数都小于原数,所以两个数的和就一定小于700+300,也就是小于1000。像这样的题目,先估算的目的在于可以先确定结论,也有利于准确计算该类题型。
2. 先算后估,检验结果
在总复习阶段,大多数的练习我们往往要求准确计算,所以大多数的学生缺乏估算的意识。笔者对2019届六年级学生做了一次简单的问卷,问卷显示全年级只有5.95%的学生具备先估后算的习惯。针对这一现象,笔者大胆提出先算后估的教学尝试,也就是在学生进行精确计算后再估算,我们把这种估算定义为验算的一种。经过尝试,我们欣喜地发现,这样的教学尝试有利于学生运算的正确率,同时也培养了学生的自信,他们纷纷表示:“我们列式的结果一定是对的。”例如,“根据第六次人口普查统计,上海市有2301.91万人,其中65周岁以上的占10.1%。65周岁以上的有多少人?”像这一类题型要求精确计算,在计算后,学生如果能再估一估——2301万人的10%是230万左右——相信对计算结果的正确率一定有很大的保证作用。通过一个学期的训练,笔者惊喜地发现,全年级已有22.2%的学生养成了先算后估的习惯。访问后得知,原来他们通过先算后估的策略发现了估算的好处,所以就开始先算后估了。
■二、简算能力的再提升
数学能力水平将运算能力界定为三个层次:第一层,能根据运算法则正确地进行运算;第二层,能在理解算理的基础上,根据运算律正确地进行运算;第三层,能寻求合理简洁的运算途径解决问题。笔者着力提升学生简算的能力,就是旨在协助学生寻求合理简洁的运算途径解决问题,同时,节省复习时间,提高复习效率。
1. 强化运算律,提高敏感度
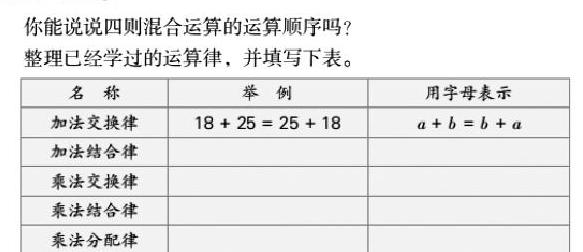
在总复习“数的运算”板块单独为运算顺序和运算律开辟了两页的复习内容。在复习时,应该尝试让学生通过举例说明、语言描述和用字母表示等方式对加法运算律和乘法运算律进行整理,并在教材中完整表格内容。(如图1)
在此基础上,让学生举例说说怎样运用这些运算规律进行有关的简便计算。笔者认为,乘法分配律是毕业复习的一个重点,也是一个易错点。例如,8+■÷4。这一题,如果要运用乘法分配律,第一步应该是先将“÷4”转化成“×■”,再应用乘法分配律进行简便计算。如果有学生把原式改写成了“8÷4+■÷4”再进行计算,也是可以的,但要引导学生运用所学知识解释其中的道理。同时应该立刻追加72÷(18+6),让学生进行对比分析。
2. 重申两性质,培养逆思维
所谓“两性质”,指的是减法的性质“一个数连续减去两个数,就等于减去这两个数的和”以及除法的性质“一个数连续除以两个数,就等于除以这两个数的积”。关于这两个性质在运算时的灵活运算,对于小部分学生来说还是有点困难的。但是,这两个性质的应用对解决实际问题十分有帮助,因此需要重申。例如,仓库里有560吨大米,现在有5辆载重量均为16吨的卡车,几次可以把大米运完?我们都知道这是一个连除的应用题,可以列式560÷16÷5。如果按照运算顺序,应该先计算560÷16,再除以5,需要列竖式计算,不方便;如果学生能够准确地掌握除法的性质,那么这道算式将转化为560÷(16×5),16×5=80,560也正好是80的整倍数,很快就能求出结果。
笔者认为“两性质”在运算中的应用,难点不在于像上题的应用,而在于逆运用。例如,5■-2■+■和■÷■×■,对于去括号后究竟如何“变符合”,是学困生的难点,有待进一步的巩固训练。笔者认为,不仅要让学生进行巩固训练,更多的应该让学生说一说为什么是这样算,道理是什么。笔者相信,坚持这样的强化训练,逆向思考,一定能为更好更快地计算提供有力的保障,学生的思维也一定能够得以进阶。
■三、解方程的再思考
解方程是五六年级接触的一类新运算。在常规的教学中,我们主要利用等式的“性质一”和“性质二”进行方程的求解;但在实际练习和運用中,我们发现还可以利用简单的数量关系求解方程。
1. 利用图式学习,有的放矢
到了六年级下学期,班级仍然会出现个别学生不会解方程,严重影响了这些学生的总复习。那么在总复习时,针对这一类学生,教师往往按照教参的要求,布置一连串的问题:什么是方程?方程与等式有什么样的关系?已经学过的等式性质有哪些?怎样应用等式的性质解方程?等等。对于一般的学生,特别是学有余力的学生,这些问题就是在浪费复习时间;但对于学习暂时有困难的学生,也不过是在课堂上快速地听着其他没有学习困难的学生几乎背着说一遍,实际上什么都没有留下,并没有起到复习的作用。
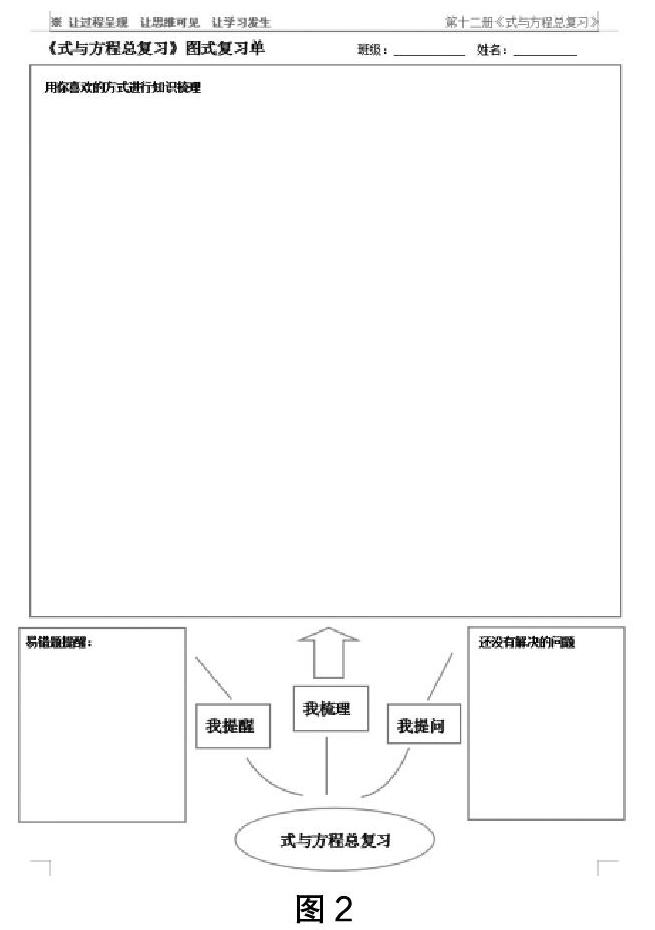
因此,笔者向大家推荐一种新的总复习方法——图式复习法。复习前,教师给学生布置一份图式作业(如图2),学生根据自己的实际情况进行“我梳理”“我提醒”和“我提问”等环节的整理。课前,教师对学生的图式复习单进行回收,收集学生共性的问题、典型的问题,课堂上有的放矢,查漏补缺,各个击破。特别是对暂时还不能全面、完整梳理知识的学生会有很大的帮助,也有助于总复习期间的因材施教。
2. 巧用数量关系,事半功倍
在一起单元检测中,我们遇到了这样的方程:■÷x=■。《义务教育数学课程标准(2011年版)》中要求:“能用方程表示简单情境中的等量关系(如3x+2=5,2x-x=3),了解方程的作用。”虽然已经回避了这一类方程,但在平时的练习中,仍然会遇到此类情况。因此针对这样的题型,笔者建议利用数量关系解决。我们知道“被除数÷除数=商”这是一个简单的数量关系,通过这个数量关系,我们延伸出“除数=被除数÷商,商=被除数÷除数”这两个数量关系。那么对这个方程的求解就可以利用“除数=被除数÷商”转化为我们常见的简易方程x=■÷■。同样的,如3■-2x=1这一类方程,我们可以利用“被减数-减数=差”的延伸数量关系“减数=被减数-差”,将方程转化为2x=3■-1。当然,利用等式性质的拓展延伸一样可以解决3■-2x=1和■÷x=■这两类方程,只是等式两边要同时加上“2x”、同时乘“x”这样的字母表达式,再利用等式的性质交换等式左右两边的表达式,转化为我们常见的简易方程。对比利用数量关系和等式性质进行这一类方程的求解,明显发现巧用数量关系,能够事半功倍。
运算能力的再提升是一个长期的过程,不是一蹴而就的,需要教师的重视。本文所列举的几点思考也是局限的,但本文认为,经过加强估算能力的培养、提高简算的敏感度、灵活选择策略进行计算的训练,在总复习阶段中绝大多数学生的运算能力一定能得到再提升。
