不同阶段的轨道交通定价模型研究

毕晓萤

(南京市城市与交通规划设计院股份有限公司，江苏 南京 210000)

为满足城市居民全天候、全人群、多样化的出行需求，应加快构建多层次公交体系，提供多样化、高品质的公交服务，增强与私人小汽车交通的竞争力。轨道交通、常规公交和出租汽车是城市公共交通客运体系的重要组成部分，在市场经济条件下，系统内部存在一定程度的客流竞争。如何设置轨道交通、常规公交、出租汽车的票价水平及相互之间的比价关系，制定恰当票制的票价体系，对于合理分配客流、引导出行者出行方式选择、进一步提升城市公共交通客运系统的整体运行效率具有重要作用。

1 出行者出行成本构成

根据“经纪人”假设，人们在出行决策中，一般不会考虑外部成本，而仅从个人成本最小化角度出发。因此，本文所提的出行成本仅考虑表示出行者的个人使用成本。现阶段研究普遍认为，个人出行成本由货币成本、时间成本和舒适性成本三部分构成[1]。

1.1 货币成本

货币成本主要指出行者在出行行为过程中的财富损失，在公共交通出行过程中是指票价支出。

1.2 时间成本

时间成本是指出行者在出行行为过程中所耗费的时间。本文通过时间成本的货币化，即出行时间乘以单位时间价值进行建模。

1) 出行者利用常规公交一次出行时耗tb，包括到公交车站时间、候车时间、乘车时间及离站时间四部分，如下式所示

(1)

式中：假设Db=Db1+Db2，为常规公交的平均站距，取值为500 m；v步为步行速度，取v步=4.4 km/h；L为出行者的出行距离；tb间为常规公交的发车间隔，取tb间=5 min；vb为常规公交的行程车速，取vb=20 km/h。

2) 出行者利用轨道交通一次出行时耗tr，包括到轨道站时间、候车时间、乘车时间及离站时间四部分，如下式所示

(2)

式中：假设Dr=Dr1+Dr2为轨道交通的平均吸引距离，取值为1.5 km；v步为步行速度，取v步=4.4 km/h；tr间为轨道交通的发车间隔，取tr间=6 min；vr为轨道交通的行程速度，取vr=35 km/h。

3) 出行者利用出租汽车一次出行时耗tc，由候车时间、乘车时间两部分组成，如下式所示

(3)

式中：tc候为等车时间，取tc候=5 min；vc为出租汽车的行程速度，取vc=25 km/h。

时间价值，主要指将出行时间折算为工作、学习、生活等活动中消耗相同时间带来的效益。按照国家计委1993年颁布的“建设项目经济评价方法与参数”规定，单位时间价值的计算公式[2]为

(4)

不同交通方式人的单位时间价值不同，即Vot不同，每一种交通方式应该对应一个价值系数。表1为不同交通方式的价值系数表。

表1 各出行方式的价值系数表[3]

1.3 舒适性成本

选取乘车稳定性程度、车内外体力消耗、车内拥挤程度、车内空气质量与温度适宜度、私密性程度和准时性程度六项指标评定公共交通的舒适性成本。六项指标的值由0～4表示，其中0表示舒适度最高，4表示舒适度最低，将六项指标加和，再乘以相对应的系数[4]，则有

(5)

式中：Cj为第j种交通工具的舒适性成本，元/人·km；β为该交通方式单位时间价值，元/h；αj为采用第j种交通工具恢复疲劳所需时间的折减系数；di为第i项舒适性影响因素等级所对应的分值；tj为采用第j种交通方式平均出行时间，h；Lj为采用第j种交通方式的平均出行距离，km。

1.4 出行成本权重

根据苏州市轨道交通出行意向调查[5],对回收问卷进行统计，如表2所示。

表2 出行影响因素统计情况

公交票价、出行时间、舒适性分别用X1、X2、X3表示，从表2可以看出X1与X2相比，X2重要；X1与X3相比，X3稍重要；X2与X3相比，X2稍重要，基于层次分析法确定各影响因素权重。

1)建立比较矩阵

2)用和法计算权重

3)进行一致性检验

通过Matlab计算矩阵的特征值，求得矩阵特征值λmax=3.038。

因此，出行者意向调查结果的不一致性检验通过，解得的权重系数W可靠。即公交票价、时间成本、舒适性成本在出行者出行过程中的权重分别为0.103、0.605、0.292。

1.5 出行者广义出行成本函数

假设在出行行为过程中有N种交通方式可供选择，那么第k种交通方式的广义出行成本TCk可用下式表示

TCk=aPk+bTTCk+cCk.

(6)

式中：Pk为第k种交通方式的票价；TTCk为第k种交通方式的出行时间成本；Ck为第k种交通方式的舒适性成本；a,b,c为三类出行成本的权重系数。

2 城市公交票价制定方法研究

2.1 不同时期公交定价目标和策略

轨道交通的发展可分为发展初期、发展中期和发展后期三个时期。不同时期轨道交通企业所面临的市场环境、运营成本和竞争力具有较大的差异性，应制定不同的定价目标和策略[6]。

轨道交通发展初期，轨道交通应培育大量的稳定客流，建立轨道交通最大程度地吸引客流模型；发展中期，轨道交通、常规公交和出租汽车三者竞争较为激烈，为促进公交系统中不同方式之间的有效配合和高效运行，应建立伯特兰-纳什均衡模型；发展后期，轨道交通在市场竞争中占据优势，常规公交和出租汽车应配合轨道交通，完成整个城市的公共客运任务，此时应建立公交票价的双层规划模型。

2.2 发展初期：轨道交通最大程度吸引客流模型

城市在引入轨道交通初期，公共客运市场的客流会重新分配，市民出行交通方式选择处于一种非稳定状态。假定此时常规公交和出租汽车的票价不变，可建立轨道交通最大程度吸引客流模型，确定其票价水平。

运量Q与票价P之间的函数关系可用下式表示[7]

Q=aPτ.

(7)

式中：Q为轨道交通年运量，人/次；P为轨道交通平均成本票价，元；τ为运量的价格弹性系数；a为常数。

所以可得

lnP=c+lna-lnQ.

(8)

轨道交通最大程度吸引客流的票价为

(9)

借鉴广州地铁一号线数据，利用方程(8)求解常数a与c。

表3 广州市地铁一号线初期客流量与票价变化情况

轨道交通发展初期，为使轨道交通吸引客流最大化，可充分利用轨道交通的运能优势，轨道交通票价可制定为

2.3 发展中期：基于伯特兰-纳什均衡模型的城市公交定价

轨道交通尚未具备明显的网络化特征，即轨道交通尚未成为城市公共交通的主体方式时，其与城市客运系统中其他运输方式(常规公交、出租汽车)存在着较为激烈的竞争关系。本文提出一种描绘城市轨道交通与常规公交、出租汽车之间竞争关系的模型，即选择博弈论中描述价格竞争的伯特兰-纳什均衡模型，描绘三者之间的票价竞争，从而设置合理的相互比价模型，促进公交系统中不同方式之间的有效配合和高效运行。

2.3.1 出行方式选择概率模型

基于交通状况的复杂性，导致出行者对交通方式的选择具有一定的随机性。相关研究一般选取概率选择模型来表征这种随机性。其中，Logit模型是应用最广泛的模型，其基本形式如下[8]

(10)

式中：Pijr为交通区i到交通区j，交通方式为r的分担率；Cijr为交通区i到交通区j，交通方式为r的交通阻抗；Cijk为交通区i到交通区j，采用交通方式k的交通阻抗；θ为待定系数。

2.3.2 轨道交通、常规公交及出租汽车的票务收入模型

1)轨道交通运营者的票务收入为

Rr=Qr×Pr=

2)常规公交运营者的票务收入为

Rb=Qb×Pb=Q×

3)出租汽车运营者的票务收入为

Rc=Qc×Pc=Q×

式中：Q为城市客运系统的总客流量；Rr,Rb,Rc分别为轨道交通、常规公交和出租汽车运营者的票务收入；Qr,Qb,Qc分别为轨道交通、常规公交和出租汽车的客流量；Pr,Pb,Pc分别为轨道交通、常规公交和出租汽车的票价。

2.3.3 轨道交通、常规公交、出租汽车的价格博弈模型

轨道交通、常规公交和出租汽车三者的运营者是互相竞争的寡头，他们可根据其他两方的票价来调整自己的票价，即伯特兰-纳什均衡模型。

轨道交通运营者在运能满足条件下追求票务收入最大化，即

(11)

式中:Qrm为轨道交通所能承受的最大客流量，Prm为政府对轨道交通的最高限价。

令Qrm/Q=ξr，ξr为轨道交通在城市客运系统中的最大分担率，解式(11)得到Pr为Pb和Pc的隐函数，即Pr=fr(Pb+Pc)，为轨道交通运营者对常规公交和出租汽车运营者的反应函数。

同理，Pb为Pr和Pc的隐函数，即Pb=fb(Pr+Pc)为常规公交运营者对轨道交通和出租汽车运营者的反应函数；Pc为Pr和Pb隐函数，即Pc=fc(Pr+Pb)，为出租汽车运营者对轨道交通和常规公交运营者的反应函数。

该伯特兰-纳什均衡的解为三种交通方式反应函数的交点，即

(12)

2.4 发展后期：基于双层规划模型的城市公交定价

随着轨道交通线路条数、里程、站点数量的增加，其吸引力也相应提高。当轨道交通逐步成为公共交通主体时，其网络特征将得到很大发挥。因此，当轨道交通网络效益到达一定程度后，如果合理制定票制，票价将会进一步推动市民出行方式的优化，充分发挥轨道交通的运能，实现公共交通资源的高效配置。

2.4.1 符号说明

轨道交通发展后期，出行者可实现便捷换乘，因此在交通分配过程中，几乎不存在路径的选择问题，而只有方式的选择问题。假设每对起讫点间，选择一种交通方式只有一种固定的运行路线，这样，当出行者选定交通方式后，出行线路也随之确定。

W：OD对的集合；

N：交通方式的集合；

n=r,b,c：分别为城市轨道交通、常规公交、出租汽车；

Qw：OD对w之间的交通需求；

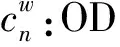
2.4.2 用户出行选择模型

根据Wardrop提出的流量均衡分配原则：当出行者选择出行方式时，有出行者使用的交通方式广义出行成本均相等，且小于或等于未被使用的交通方式的广义出行成本。其数学形式可描述为

为研究固定需求条件下，出行者的出行方式选择行为，本文构建以下的数学规划模型

2.4.3 管理者模型

根据以上分析，出行者总是选择广义出行成本最小的交通方式。因此，通过上述模型可以得到在各类成本及各种交通方式运输能力等因素已经确定的情况下，客运总量在不同的交通方式之间的分配情况。以此为基础，可以建立双层规划模型来寻求城市轨道交通的最佳票价策略，以实现期望目标。

此时，城轨道交通、常规公交和出租汽车运营者的目标均为票务收入最大化。

出行者可根据货币成本来调整自己的出行方式选择，从而进一步影响各类交通方式运营者的票务收入，这是一个Stackelberg博弈，可以利用双层规划模型描绘博弈各方的行为。综合以上可得到以下关于城市公共交通票价制定的双层规划模型

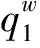
下层用户出行选择模型中的阻抗函数本文采用幂函数的形式

Vr=aPr+bTTCr+cCr.

式中：Pr,TTCr,Cr分别为轨道交通的货币成本、时间成本、舒适性成本；k,b为待定参数。

3 南京市实例分析

3.1 轨道交通运营初期

2005年9月，南京首条轨道交通开通运行。2006年轨道交通客运量达到8015.56万人次[9]，由式(10)可得轨道交通票价为P0=2.32元/次。

3.2 轨道交通运营中期

截至2016年底，全市营运地铁线路已达6 条，分别为1 号线、2 号线、3 号线、10 号线、S1 机场线、S8 宁天线，地铁运营线路长度达到224 km，站点总数121 个，基本步入轨道交通运营中期。

3.2.1 单位时间价值

2016年，南京市人均地区生产总值127 264元[10]，单位时间价值为43.58元/h。

3.2.2 出行时间成本

根据居民出行调查[11]，2016年南京市居民利用常规公交平均出行时耗tb=44.5 min；轨道交通平均出行时耗tr=54.0 min；出租汽车平均出行时耗tc=37.9 min。所以，常规公交、轨道交通、出租汽车出行时间成本分别为：2.64元/人·km，2.03元/人·km，2.61元/人·km。

3.2.3 舒适性成本

可参照南京市公共交通与小汽车舒适性指标等级评定的统计结果[12]，公交车、地铁和出租汽车评级分别为14.05、5.02、3.91。此外，当出行者采用交通方式不同时，对于疲劳的心理定位也会不同，需要恢复疲劳的时间不同。不同交通方式对疲劳时间的折减系数取值如表4所示。

表4 不同交通方式对疲劳时间的折减系数[12]

由式(5)可得到2016年南京市常规公交、轨道交通和出租汽车的出行舒适性成本，如表5所示。

表5 2016年南京市乘客出行舒适性成本

3.2.4 广义出行成本

由式(6)可得到2016年南京市常规公交、轨道交通、出租汽车的广义出行成本

Cb=0.103Pb+1.96(元/人·km)，

Cr=0.103Pr+1.33(元/人·km)，

Cc=0.103Pc+1.64(元/人·km).

3.2.5 票价计算

取ξr=0.85,ξb=0.45,ξc=0.30，解式(12)可得Pr=4.36元，Pb=4.25元，Pc=7.76元，即轨道运营中期，票价宜定价为均价4.36元/次。

3.3 轨道交通运营后期

截至2017 年底，南京市轨道网络进一步加密，全市营运地铁线路达到9 条，运营线路长度达到347.38 km，站点总数164 个。2017年，南京市轨道交通客运量97 741万人次，首次超过常规公交客运量(89 802.4万人次)，开始占据公共交通主体地位。

3.3.1 单位时间价值

2017年，南京市人均地区生产总值141 103元[13]，单位时间价值为48.32元/h。

3.3.2 出行时间成本

根据居民出行调查[14]，2017年南京市居民利用常规公交平均出行时耗tb=45.0 min；轨道交通平均出行时耗tr=49.5 min；出租汽车平均出行时耗tc=38.6 min。所以，常规公交、轨道交通、出租汽车出行时间成本分别为：2.92元/人·km，2.39元/人·km，2.88元/人·km。

3.3.3 舒适性成本

由式(5)可得2017年南京市常规公交、轨道交通和出租汽车的出行舒适性成本，如表6所示。

表6 2017年南京市乘客出行舒适性成本

3.3.4 广义出行成本

由式(6)可得2017年南京市常规公交、轨道交通、出租汽车的广义出行成本为

Cb=0.103Pb+2.17(元/人·km)，

Cr=0.103Pr+1.56(元/人·km)，

Cc=0.103Pc+1.81(元/人·km).

3.3.5 票价计算

轨道交通、常规公交、出租汽车的阻抗函数分别为

本问题的双层规划模型可写成下式

maxZr=q1pr，

s.t. 0≤p1≤10，

pb=3,pc=15，

s.t.qr+qb+qc=1 000.

将p1=5作为初始值代入上式，得到配流结果为：qr=298.18,qb=340.08,qc=361.74。

利用灵敏度分析法找到客流量对其货币成本的导数，即

y=[q(p),p]T.

得到

将已知数据带入到矩阵中

▽y=[Jy]-1[-Jp]=

利用泰勒展开公式可得到不同交通方式对应的客流量与票价之间关系

从上式可知，轨道交通出行者需求量与票价的导数为：∂q/∂p=-52.99。

令qr(pr)=298.1852.99(p1-5)，代入上层目标函数中，有maxZr=pr[298.18-52.99(pr-5)]。

同理可得

maxZb=pb[340.08-55.24(pb-3)],

maxZc=pc[361.74-56.37(pc-15)].

解上式得：pr=5.31元，pb=4.58元，pc=10.71元，即轨道运营后期，票价应定价为均价5.31元/次。

4 结 语

本文以城市轨道交通发展时序为轴线，结合轨道交通发展过程不同时段具有的不同特点，根据轨道交通发展初期、中期、后期，提出不同定价模型来确定城市公共交通的票价水平。前期建立轨道交通最大程度吸引客流模型；中期建立伯特兰-纳什均衡模型，是一种基于价格的寡头竞争模型；后期建立双层规划模型，上层为各交通方式的运营者票务收入最大化模型，下层为用户出行选择模型。轨道交通运营初期，低票价促进了客流的快速增长，充分发挥了轨道交通的社会效益。随着轨道交通的建设，应结合轨道交通发展时序适时调整票价，既减轻政府的财政负担，又保障轨道交通的可持续发展。