高速铁路动态票价制定策略
2020-01-18于展
于 展
(北京交通大学,北京 100044)
我国高速铁路经过了十多年的发展,带动了经济社会的快速发展,当前仍在大规模建设阶段。高速铁路的运营会迎来市场化改革后的巨大挑战,巨大的投资必须要考虑成本回收和运营收入。民航运输充分利用价格杠杆,不断推出折扣机票和各种优惠手段吸引顾客,客流不断増加运营收入不断改善。在中长途运输市场中,高铁与民航竞争激烈,民航运输在竞争中不断完善票价机制,保证了较高的上座率;反观高速铁路的票价机制,2016年开始中国铁路总公司刚刚获得了200 km以上的高速铁路动车组的一等、二等客座票价的定价权,就显得票价单一没有折扣票价吸引旅客[1]。
国外的高速铁路发展较早,在经历了多次改革后,大都形成了成熟的票价体系,其共同特点就是市场化定价,票价的制定充分考虑了不同人群的需求特征、运输市场的竞争状况、社会福利的倾斜,推出适合不同群体、不同时间的票价。我国经济欠发达地区的高速铁路旅客上座率较低,在客流非高峰期时单一的票价缺乏对旅客的吸引。固定的定价机制制约了铁路行业的发展。我国必须在高速铁路的票价问题上进行完善,充分考虑基准票价的制定,使其符合当前的经济发展水平;改变当前的单一票价现象,优化票价制定方案,实行不同时期的浮动票价,分析旅客的不同运输需求进而推出不同的票价种类。随着经济发展和高速铁路的大规模投入运营,高速铁路的发展面临越来越严峻的市场竞争,铁路发展必须不断推进市场化改革,逐步实施市场化定价机制。
1 需求调查
为了更好地刻画旅客偏好,我们进行了关于高铁旅客出行行为的调查的问卷,本模型中,仅应用了问卷的部分数据。根据问卷调查得到旅客对于高铁二等座座位的选择偏好。虽然问卷数量有限(回收有效问卷数7080份),但依然可以看出旅客对于高铁座位选择倾向有显著差异。61.72%的旅客选择座位F,近21.89%的旅客选择座位A,近11.3%旅客选择座位D,极少数旅客选择座位B(2.4%)和C(2.68%)。该数据将作为后续基于需求满意度的浮动票价定制的指标依据,随着后期数据量的扩大,将得到更加符合实际情况的数据。
2 模型构建
本文在借鉴国内外高铁及航空票价体系的基础上,建立了一个基于线路余票历史数据、旅客对二等座不同类别选择偏好的动态票价定制体系。采用数据驱动的方法,通过以客票预售期内客流需求变化情况来预测明日售票率。建立数据库,按照假定条件进行筛选,并使用优度检验的方法,动态更新数据库。本模型中高铁票价由基础票价及票价浮动百分比构成。在考虑基础票价制定时,在当前实际票价的基础上,加入起迄点经济发展水平的因素, 在一些经济水平发展较好的线路上适当提升高铁价格,在经济水平发展较落后的线路上适当降低高铁价格,使得高铁运价更符合线路本身的经济发展水平。在考虑票价浮动百分比时,通过刻画旅客的偏好因子,并使其与票价浮动程度建立联系,由此表达出票价浮动百分比。
2.1 问题描述及假设
设从地点A到地点B某一班次高速铁路列车在预售期共存在I张可供销售的车票,为方便对单个旅客进行分析,将高速铁路客票发售周期平均分成M个子周期,当M足够大时,可使得每个子周期内最多只有一个旅客有出行意愿,可将购票人数转变为购票概率。
当旅客有出行意愿,并且实际高铁票价低于旅客的保留价格时,旅客将会发生购票行为。设一个旅客在每个周期内有出行意愿的概率为g(t),那么该旅客在该周期内旅客不具备出行意愿的概率为1-g(t)。同时假设客票价格为x时,所有访问旅客的保留价格分布函数是F(x),其密度函数是f(x),p是旅客的保留价格,旅客保留价格分布函数描述的是旅客对客票价格的承受能力。我们认为,只要客票价格p≤x,旅客就会发生购票行为。当客票价格为p时,每个销售周期内有客票售出的概率为g(t)F(p)。用G(t)表示销售周期内有客票售出的概率,即G(t)=g(t)·F(p)。
2.2 模型建立
令t=1,2,…,T表示当前周期到预售期结束剩余的周期数。V(i,t)表示当剩余周期数为t,剩余客票数为i时,从当前周期起至总发售期结束所能得到的最大总收益。利用Bellman提出的随机动态规划公式可推导出高速铁路客票价格的期望收益的递推公式为:

F(p)V(i,t-1)]+(1-g(t))V(i,t-1)}=
V(i,t-1)]+V(i,t-1)}=
maxp{G(t)[p+V(i-1,t-1)-
V(i,t-1)]+V(i,t-1)}.
(1)
根据假设,我们认为当售票周期结束或无剩余客票后不再产生其他收益。因此边界条件为:
1)V(i,0)=0,∀i,表示售票周期结束,不再产生收益;
2)V(0,t)=0,∀t,表示该车次无客票剩余,不再产生收益。
明显地,对于给定剩余客票数i,V(i,t)随剩余周期数t的增加而增加;对于给定剩余周期数t,V(i,t)随剩余客票数的增加而增加。
2.3 性质分析
性质1:在剩余客票数i一定的情况下,最优收益函数V(i,t)是关于剩余周期数t的凸函数。
证明:令p′为剩余客票数为i,剩余周期数为t时的客票价格;同时令p为剩余客票数为i,剩余周期数为t+1时的客票价格,0≤t≤T-1。
根据式(1)可知:
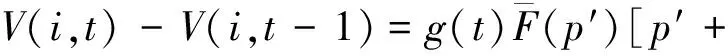

V(i-1,t-1)]-V(i,t-1).
(2)
V(i,t+1)-V(i,t)=
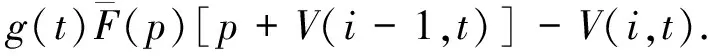
(3)
式(2)减式(3)得:
V(i,t)-V(i,t-1)-[V(i,t+1)-V(i,t)]=
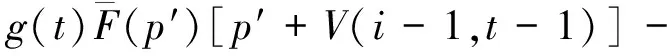
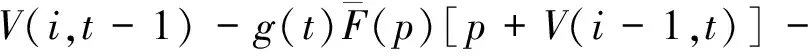
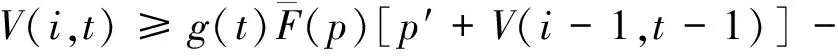
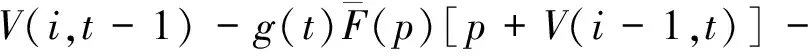
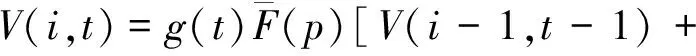
V(i,t)-V(i,t-1)]-V(i-1,t)].
(4)
由于最优收益函数V(i,t)具有上可加性,即:
V(i,t)+V(i-1,t-1)≥
V(i,t-1)+V(i-1,t).
(5)
可知
V(i,t)+V(i-1,t-1)-V(i,t-1)-
V(i-1,t)≥0.
(6)
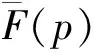

V(i,t-1)-V(i-1,t)]≥0.
所以可得(7)式:
V(i,t)-V(i,t-1)-V(i,t-1)-V(i,t)]≥0,
整理可得2V(i,t)≥V(i,t-1)+V(i,t+1).
因此V(i,t)是关于剩余周期数t的凸函数。
性质2:在剩余周期数t给定的情况下,最优收益函数V(i,t)是关于剩余客票数i的凸函数。
证明:令p′为剩余客票数为i+1,剩余周期数为t+1时的客票价格;同时令p为剩余客票数为i,剩余周期数为t+1时的客票价格,0≤t≤T-1。
根据式(1)可知:

V(i,t)-V(i+1,t)]+V(i+1,t)-
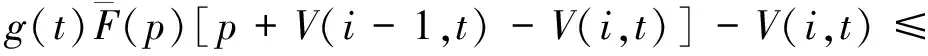
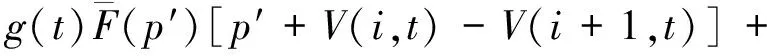
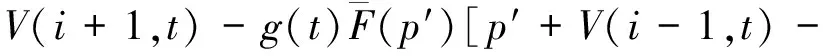
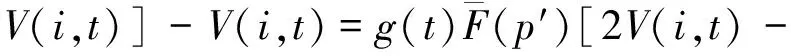
V(i+1,t)-V(i-1,t)]+V(i+1,t)-V(i,t).
由式(5)可知:
V(i+1,t)-V(i,t)≤V(i+1,t+1)-V(i-1,t).
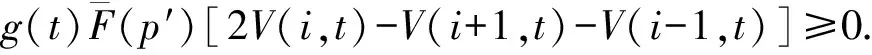
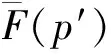
2V(i,t)-V(i+1,t)-V(i-1,t)≥0.
因此V(i,t)是关于剩余客票数i的凸函数。
性质3:在剩余客票数i一定的情况下,价格策略p(i,t)是关于剩余周期数t的非减函数。在剩余周期数t一定的情况下,最优价格策略p(i,t)是关于剩余客票数的非增函数。
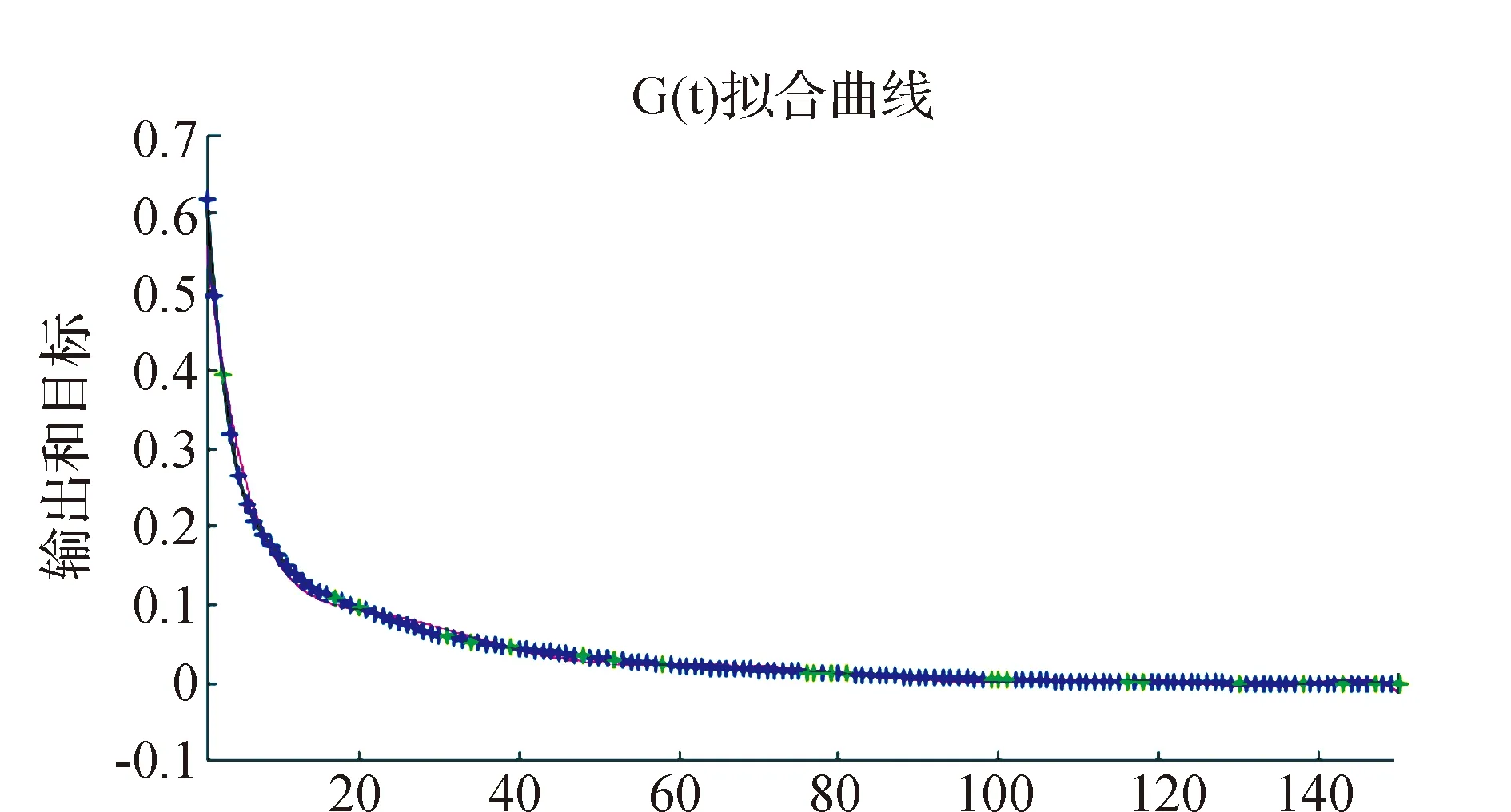
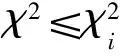
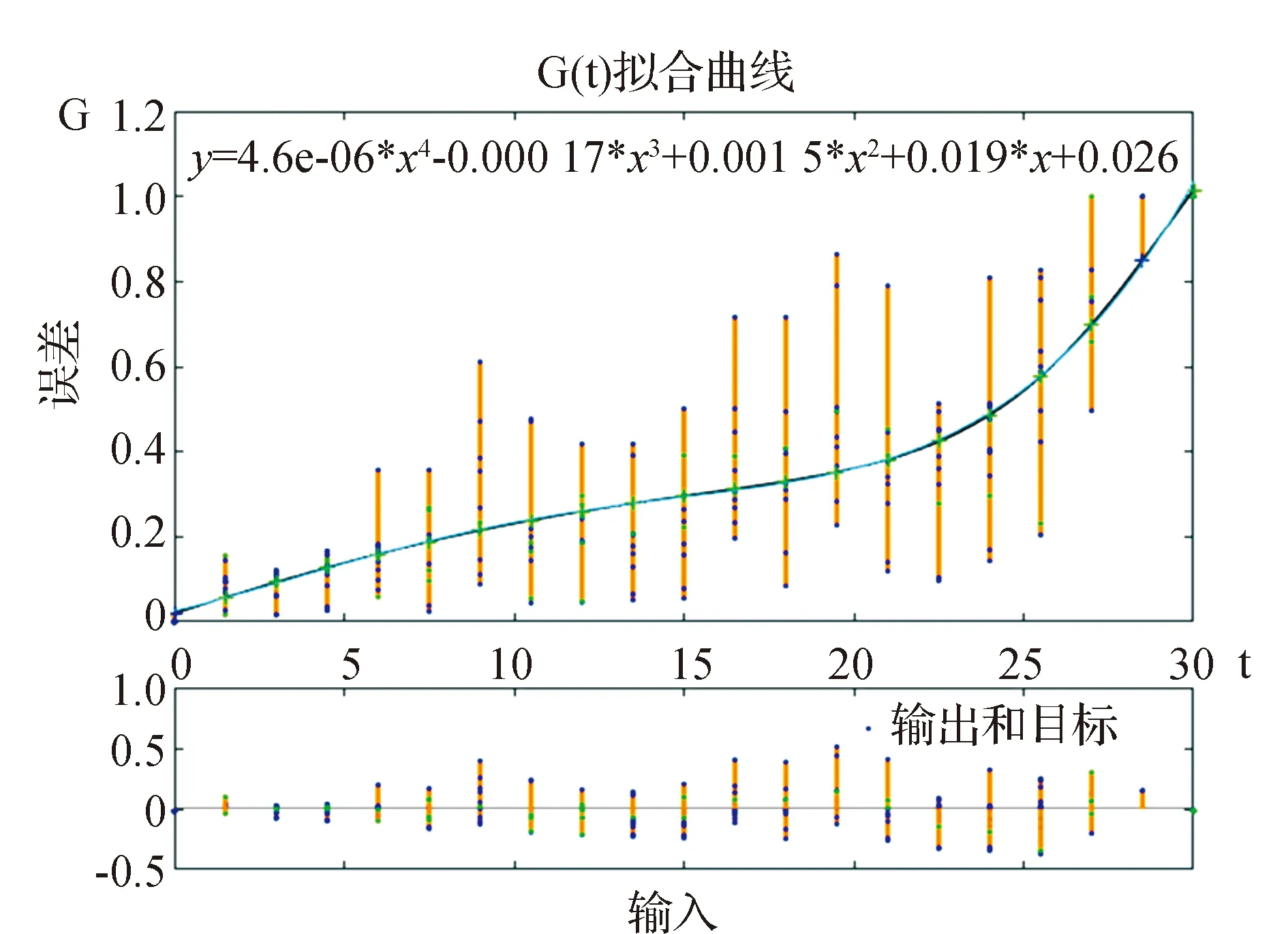
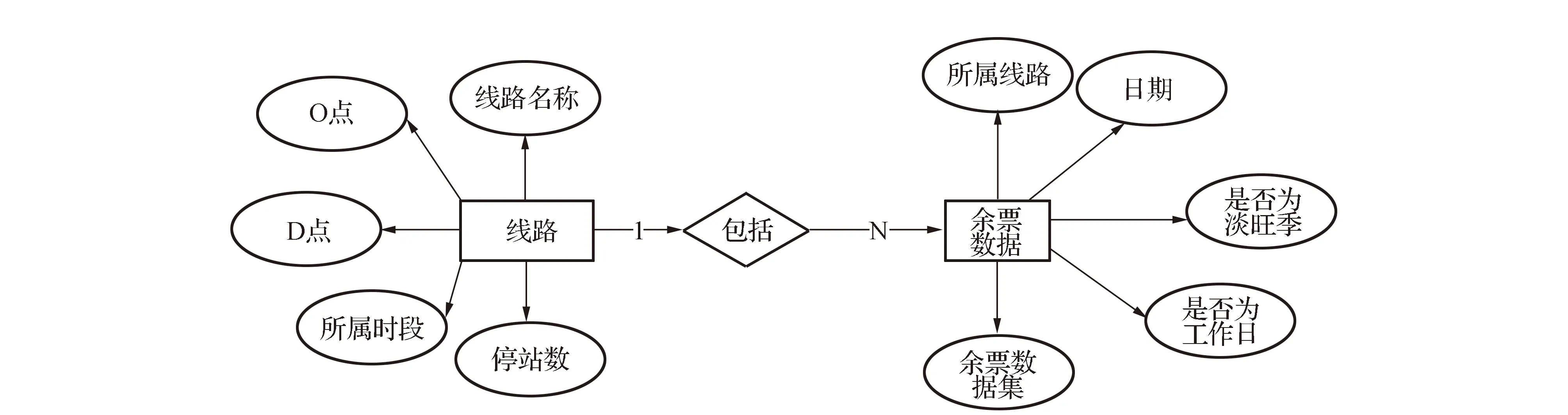
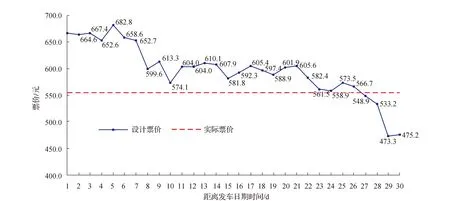
证明:(1)令p为客票状态为(i,t)时的最优价格,设m为任意小于最优价格p的客票价格,0 V(i-1,t-1)]+V(i,t). 由此条件可知: 由式(5)可知: V(i,t)-V(i,t-1)-V(i-1,t)+ V(i-1,t-1)≥0. 所以 这就表明在预售期客票状态为(i,t+1)时,采用任何小于客票状态为(i,t)的客票价格p的价格所取得的收益都小于采用客票价格p所取得的收益。那么预售期客票状态为(i,t+1)时的价格策略p(i,t+1)一定不小于p(i,t),所以在剩余客票数i一定的情况下,价格策略p(i,t)是关于剩余周期数的非减函数。 令p为客票状态为(i,t)时的最优价格,设n是任意大于(i,t)状态下的最优价格p的客票价格,0 由假设条件可知V(i,t,n) 整理可得: 已证明最优收益函数是关于剩余客票数的凸函数,那么: 2V(i,t-1)≥V(i+1,t-1)+V(i-1,t-1), 即V(i,t-1)-V(i-1,t-1)≥ V(i+1,t-1)-V(i,t-1). 式(6)可以写为: V(i+1,t-1)]+V(i+1,t-1)}- V(i+1,t-1)]+V(i+1,t-1)}= V(i+1,t,n)-V(i+1,t,p). 即V(i+1,t,n) 由此可以看出在预售期客票状态为(i+1,t)时,采用任何大于客票状态为(i,t)时的最优客票价格p的价格所取得的收益都小于采用客票价格p所取得的收益。那么预售期状态为(i+1,t)时的最优价格策略p(i+1,t)一定不大于p(i,t)。所以在剩余周期数t一定的情况下,最优价格策略p(i,t)是关于剩余客票数i的非增函数。 G(t)表示销售周期内有客票售出的概率,利用某条线路高铁动车组列车发车前1 d至发车前30 d的每日余票数据,相邻两天数据作差得到预售期内每日的售票数据,通过MATLAB进行BP神经网络拟合,可以分析出该线路售票数量与提前购票天数的联系,再除以该车次在开始售票时的售票数量,得到某线路的G(t)曲线,如图1所示。 图1 matlab拟合曲线 基于大量的余票数量数据,将建立包含所有高铁线路的G(t)曲线数据库,并随着每条线路的发车,对数据库进行补充。 根据某线路的OD点信息:发车日期是否为淡旺季;发车日期是否为工作日;发车时刻所属时段,(例如8:15发车属于8:00—9:00这一时段);停站数。这些指标,对数据库中符合的一组发售线路G(t)曲线进行筛选,计算出这组曲线预售期内每天售票率的一阶中心矩,进行拟合,作为初始的预测曲线G*(t)。对预测出的G*(t)曲线进行校正,对曲线进行优度检验: 1)将观测值分为k组 ; 2)实际每日售票数,记为Oi; 3)根据预测出的线路G(t)曲线,计算每组的理论频率为Ti; 5)在置信水平α=0.01的条件下进行检验; 递推公式中p:剩余客票数为i、剩余周期数为t时的客票价格,0≤t≤T-1。 p=pB*α(t),其中pB为基础票价,即现行的高铁票价。α(t)为票价浮动百分比,通过引入偏好因子β同α(t)建立联系。 α(t)与G(t)及旅客对于座位的选择偏好有关, 根据问卷中旅客对于不同类别座位的偏好比例,看出旅客对于F、A、D三类座位的偏好占95%,因此在对票价进行浮动时,对60%的座位的票价进行上浮,对其余40%的座位的票价进行下调。设定票价上浮比例最大值为a,下调比例最大值为b。将不同时段的G(t)与通过问卷得到的旅客对于不同座位偏好的百分比相乘得到偏好因子β,即β=G(t)*θ用来刻画预售期内不同时段旅客对于不同类别座位的偏好程度,将偏好因子β与票价上下波动范围建立联系,以此对票价进行浮动。 偏好因子β与α(t)通过如下方式建立联系: 将预售期内1~30 d的售票率与乘客对5种座位的偏好概率相乘,得到150组数据,降序排列,通过BP神经网络拟合出偏好因子曲线,易知,β的最大值即为乘客对于F座位的偏好概率0.617 2,β的最小值为0。 在对票价进行浮动时,对60%的座位的票价进行上浮,对其余40%的座位的票价进行下调,通过对坐标轴进行平移,使得曲线60%处的β=0,最终选取[-b,a]部分的浮动因子曲线。由此得到预售期不同时间段内不同类别座位对应的票价浮动比例,如图2所示。 图2 票价浮动比例区间 使用数据爬取技术,获得京沪线上G1、G3、G5等车次,在10-06—26(即发车前1 d至发车前20 d)的每日余票情况,I=1216,通过MATLAB对数据库中各条数据进行读取及神经网络拟合得到的售票率——开售日期曲线G(t),进而得到g(t)的数据,如图3所示。 根据前文得到的偏好因子,运用线性关系直接寻找其与票价浮动比例的关系。 偏好因子最高值0.348 1对应到上浮比例最大值0.2,根据二者比例关系计算出其余待上浮票价的偏好因子对应的浮动比例值;同理,下浮部分采用与上浮部分相同的比例值,且根据偏好因子最低值0.005 1与其对应的下浮比例最大值-0.2,计算出其余偏好因子对应的下浮比例。得到偏好因子与票价浮动比例对应值,见表1。 图3 开售日期曲线G(t) 为简化模型计算难度,考虑旅客对价格的反应是线性的,则旅客保留价格密度函数是一个常数函数,即每一个单位价格的变化对应的增加或减少的客票需求人数是一样的。 根据模型思路,使用“IntelliJ IDEA专业版”作为开发环境,使用“JDK8”,完成以java语言面向对象为基础的模拟仿真。仿真模拟类如图4所示。 采用蒙特卡罗算法建立仿真中心进行数值仿真,程序计算结果如图5所示。 表1 偏好因子与浮动比例的关系 图4 方针模拟类 图5 仿真结果展示 本文基于大数据技术,采用数据挖掘技术对预售期内旅客有出行意愿的概率进行预测,并结合乘客的内心接受价格、提前购票天数、对不同类型座位的偏好确定偏好因子β,采用偏好因子β表示预售期内不同时段旅客对于不同类别座位的偏好程度,基于偏好因子β对票价进行调整,以实现满足旅客需求的情况下确保总收益达到最大。经数值模拟验证,在保证乘客满意度不变的情况下,发车周期内可使利润上浮28%,可见浮动票价制具有实施的可行性。 此外本文为铁路总公司提供一种高速铁路动态票价定制策略,在定价时考虑了不同乘客的内心接受价格、提前购票天数、对不同类型座位的偏好等因素,使得用户市场得到细分,充分考虑旅客需求,在提高乘客满意度的同时,增加运输企业的经济效益和社会效益,加快运输企业市场化进程,提高高速铁路在客运市场的竞争力。
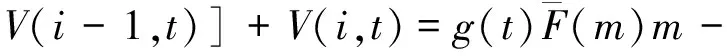
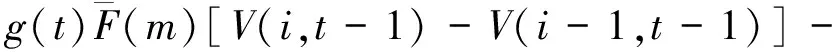
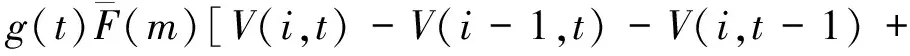
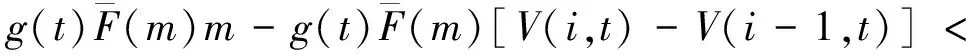
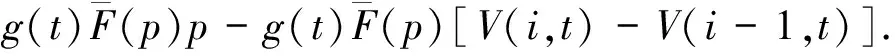
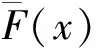
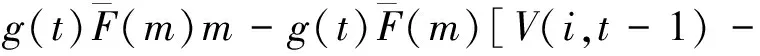
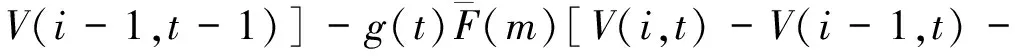

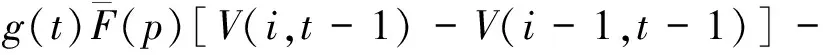
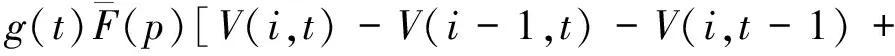
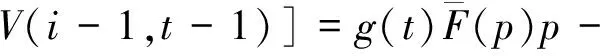
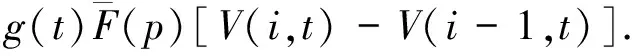
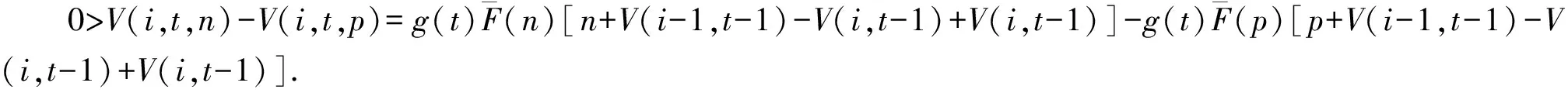
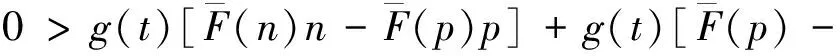
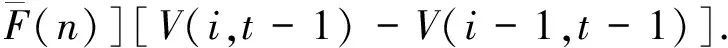
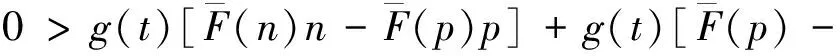
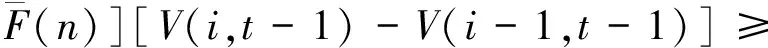
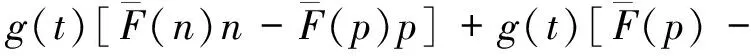
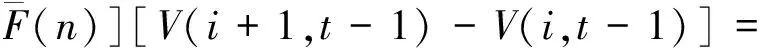

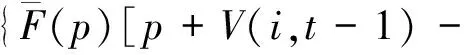
2.4 G(t)曲线数据库的建立
2.5 基于数据库对待发售线路G(t)曲线进行预测
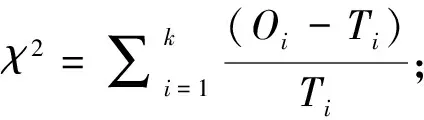
2.6 基于浮动因子确定最终票价

3 算例验证

4 结 论
