贝叶斯网络对隧道施工风险评价研究

吕 杉

(湖北工业大学 土木建筑与环境学院，湖北 武汉 430068)

随着城市轨道交通的快速发展，我国各地城市相继修建了轨道交通系统。轨道交通建设项目具有工程量大、施工技术要求高、未知因素多等特点，除此之外，轨道交通在施工过程中发生安全事故的风险也呈现增长之势[1]。鉴于此，对隧道施工安全风险评价开展研究就显得十分紧迫。

国内的安全评价方法主要运用在桥梁转体、地下洞室、岩溶隧道涌水等风险评价研究中，有关隧道施工的风险评价研究较少[2]。当前学者通常采用的都是信息量(IM)法、人工神经网络图(AN)法、支持向量机(PSO)法、决策树(DT)法及专家系统打分法等传统方法，这些方法最大的局限性是在复杂多变的系统中，不确定性分析和推理存在诸多问题。同时，与其他建设项目相比，地铁轨道交通具有耗时长、技术要求多、受周围环境影响大等特点，其次，地下未知而不确定因素较多，与此伴随的地铁工程事故频发，因此，探讨新的方法用于不确定性复杂问题的研究更具有应用价值[3]。

贝叶斯定理是由英国学者托马斯·贝叶斯提出，主要解决不确定性分析以及不完整性问题，能够在不确定性评价中解决知识表示、判断、预测等复杂问题[4]。国内外学者认为复杂的、多致险因子的风险评价具有较大优势。因此，本文基于贝叶斯定理，通过对地铁轨道交通施工过程风险管理的研究[5]，结合相关互信息理论，构建不确定性模型，并将先验知识(Prior Knowledge)和观测事件(证据)相结合，从不同方面进行了不确定性评价研究，从而达到了对地铁轨道施工风险的评价研究目的。

1 贝叶斯定理简介

贝叶斯网络(BN)是一种基于《概率论》并经过运算而组成的数字化模型，它能依托强大的数字逻辑推理计算功能以及以数字化的方式直观地表达模型计算结果的优点，在不确定性分析和推理问题方面备受好评。在天气预报、滑坡易发性评价、地震预测、医疗诊断等诸多跨专业领域，通过收集的指导性先验知识和信息数据，贝叶斯网络可以将所建立的模型定性推理到达不确定分析的目的[6]。贝叶斯的本质就是一个“矢量无边界”图，由代表变量的节点和与节点相连而形成“有向弧”。

假设在一个有向图中，如果由节点M指向节点N，那么节点M对节点N起控制作用，我们将节点M称之为节点N的父节点，节点N为节点M的子节点；如果节点M有且只有一个子节点，那么就将节点N作为根节点。运用概率公式来表达其中的关系，假如一个节点无父节点，则采用先验知识概率进行数据表达，此时的根节点就是先验概率(边缘概率分布函数)，其他节点都以根节点为条件组成条件概率分布函数[7]。

记为P(μi|μπi)，其中μπi为父节点的取值，与节点μ1，…，μn的概率相乘就可得到与之相对应的联合分布概率

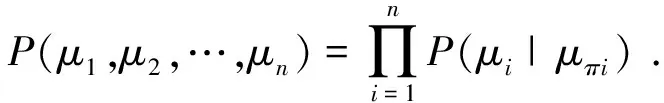
(1)

2 贝叶斯网络对隧道施工风险的评价研究流程

基于贝叶斯定理对隧道施工风险进行评价，可以为施工方提供可行性技术支撑。其风险评价流程可分为以下五个步骤：

2.1 风险识别

首先，结合地铁施工事故数据、专家经验、调查结果等资料，定性地将地铁轨道施工过程与现场施工安全管理相关的所有风险因子进行划分及分类，以清单的形式列举本工程可能的风险因子，最后通过专家组讨论确定最终的风险因子[8]。

2.2 建立贝叶斯网络模型

基于确定的最终风险因子，通过专家组给出风险因子的因果关系，然后通过忆图软件绘制BN的拓扑结构。在确定的BN结构基础上明确BN的基本参数，该过程可分为两个方面：一方面是通过专家的已知经验，得到根节点的原始概率和其他节点与父节点相连的概率；第二方面是利用noisy-gate模型在得到相关数据的前提下，完成整个BN结构的CPT。

2.3 风险推理

通过贝叶斯网络(简称“BN”)的因果推理以及诊断推理研究，定性定量地判定风险因子发生的概率以及事故发生的主要原因。

1)因果推理。已知风险因子(证据)，然后进行分析计算风险因子发生的条件概率，并将其分为基于先验知识的无证据条件概率和基于现场施工过程中的样本数据证据条件概率。通过提前预测风险因子的发生概率，施工方能提前采取相应技术措施减少事故的发生概率。

假设地铁轨道施工中，已知所有风险因子μi组成的集合为证据μt，节点R(风险因子)发生的(R=Y条件下确定的)风险概率P(R=Y/μi)可计算为

P(R=Y/μi)=

P(R/Y|μ1=x1，μ2=x2,…，μn=xn)=

μi∈μt，μi∈{R,N}.

(2)

式中：n为节点个数，且每个节点为两个不同状态(Y,N);Y为节点事件发生；N为节点事件不发生；分子部分为BN向前导入的CPT,也就是所有状态已知风险因子同时发生的联合分布概率；分母部分为已知状态事件的联合分布概率[9]。

2)诊断推理。在已知事故结果的条件下，通过BN计算诊断出致险因子，并得出其后验概率。假定节点R(风险因子)为发生状态下各节点(致险因子)的后验概率分布，则第i个节点μi发生的后险概率为P(μi=Y|R=Y)，具体计算为

P(μi=Y|R=Y)=

i=1,2,3，…，n.

(3)

2.4 关联性分析

本文采用互信息的理论权衡父节点对子节点的关联度。同时，应将其他节点的影响考虑进评价单个输入节点的关联度，互信息是两个随机变量相关性的定性统计方法，其中两个随机变量A和B之间的相关性为

(4)

式中：p(a,b)为A和B的联合概率分布函数；p(a)，p(b)分别为A和B边缘的概率分布函数。

2.5 风险控制

由地铁轨道现场风险分析得出评价结果，结合风险诊断的结果，从而确定关键的风险因子，并及时采取措施加以控制。

3 工程案例分析

通过收集多个工程案例数据及专家分析报告[10]，将研究的基于贝叶斯定理对隧道施工风险的评价方法应用到安全风险等级分析和评估中，其流程步骤如下文所述。

3.1 识别相应风险因子

根据相关研究成果及事故分析报告，结合湖北工业大学BIM研究院与中建三局第一工程建设有限公司合作的深圳地铁项目的实践，统计分析出国内地铁轨道交通安全的20个风险因子[11]，统计结果如表1所示。

表1 各风险因子统计信息表

3.2 建立贝叶斯网络模型

在确定风险因子后，分析并确定风险因子之间的主要因果关系[12]。因此设定贝叶斯网络模型的基本节点，每个节点状态都分为R和N两种，图1所示反映的是地铁轨道施工拓扑结构模型。在2017年5月9日，深圳市城市轨道交通6号线6102-4标发生一起重伤事故，通过对事故的调查分析可知，由于施工方安全管理不当，在施工前没有及时采取有效控制措施并建立相应的安全应急预案，对施工中的安全隐患未能及时进行排除，因而导致事故发生。

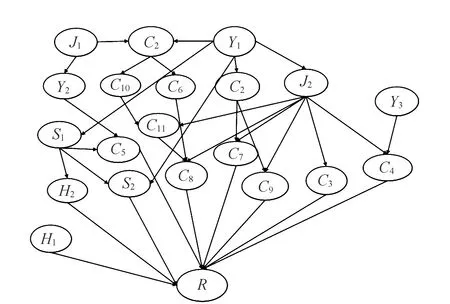
图1 BN拓扑结构模型

根节点的原始概率、其他各子节点以及与其对应的父节点连接概率都采用专家打分法的方式确定，将统计结果进行对比分析，通过专家组的论证与修订，确定最终的BN根节点的原始概率，如表2所示。

利用noisy-gate模型计算获得[13]各节点的CPT。如已知子节点C1与其父节点J1和Y1的连接概率分别为31%和28%，统计得到最终C1的条件概率，如表3所示。

3.3 正推法因果推理风险

在BN中为根节点导入其发生概率，如表2所示，计算得到其他各节点与根节点的先验概率。利用贝叶斯定理计算得到地铁轨道施工风险的先验概率值P(R=Y)=3.24%，说明该地铁施工风险相对较低。而当有证据条件导入时，证据则会通过BN向前传递，从而计算出在不同条件下风险的发生概率，如表4所示。在深圳某地铁项目风险管理过程中，已知H1(难以预知自然灾害)发生，随后在BN中导入证据值P(H1=Y)=1，采用正推法推理得到最终风险发生的概率为4.87%。

综上所述，当风险因子H1不发生时，整体安全风险会相应降低。当几个风险因子同时发生，整体安全风险增加幅度会比单个风险因子发生的增加幅度高很多[14]。因此，可以得到所建立的BN模型中各风险因子与最终的风险事故之间呈正相关。此结论与事故分析报告相吻合，从而间接证实了本文构建的BN模型的可行性。

表2 根节点的原始概率

表3 子节点C1的CPT

表4 深圳某地铁隧道施工安全预测发生概率

3.4 反推法推理诊断风险

通过BN的诊断推理理论，计算出每个风险因子后验边缘的概率值，所得具体数据如表5所示。在风险诊断过程中，后验概率值就能定性判断风险因子对风险事件的控制度。

如果在施工过程中发现风险，由表5反推法诊断后验概率可知，因施工材料、施工机械选型不满足要求(P(C4=Y/R=Y)=22.36%)的排序比较靠前，是本次事故的最可能因子。因此，在地铁施工风险事故发生后，应优先对此因子进行事故调查。如果情况属实，本次确定的P(C4=Y)=1，施工单位应采取及时有效措施防止事件进一步恶化[15]。当C4因子被控制住，则重新进行风险诊断，然后再次通过反推法推理和计算其他节点的后验概率，结果如图2所示。而此时发现C11(岗前安全教育培训不过关)的概率值最大，为19.48%，后续事故调查工作应主要从C11入手，紧接着由C11的调查结果在BN中导入新的证据，从而进行第3次反推诊断，按照此流程不断地进行循环，直到风险事故得到有效控制才终止计算。

3.5 互信息法进行易发性评价

互信息值由先验概率、后验概率及连接概率决定，由之前互信息公式计算，可得到风险事件与其父节点所代表的风险因子之间的互信息值，具体详细数据如表5所示。互信息值能定性反映风险因子对风险事件的控制程度，数值越大，说明控制程度高。因此，由互信息值大小排序可以看出各风险因子的控制程度大小。从信息表可以看出，C11、C8、C2对风险事件的控制作用更强，是目前地铁施工安全风险最应该注意的地方，应加强监督与管理。在排序的前9位中，除了现场环境两个因子外，其余7个因子都来自施工阶段，而施工方是施工阶段的最主要参与发，说明在地铁工程建设全生命周期里，施工阶段是事故的高风险阶段。因此，对地铁施工阶段的安全风险应重点监督。

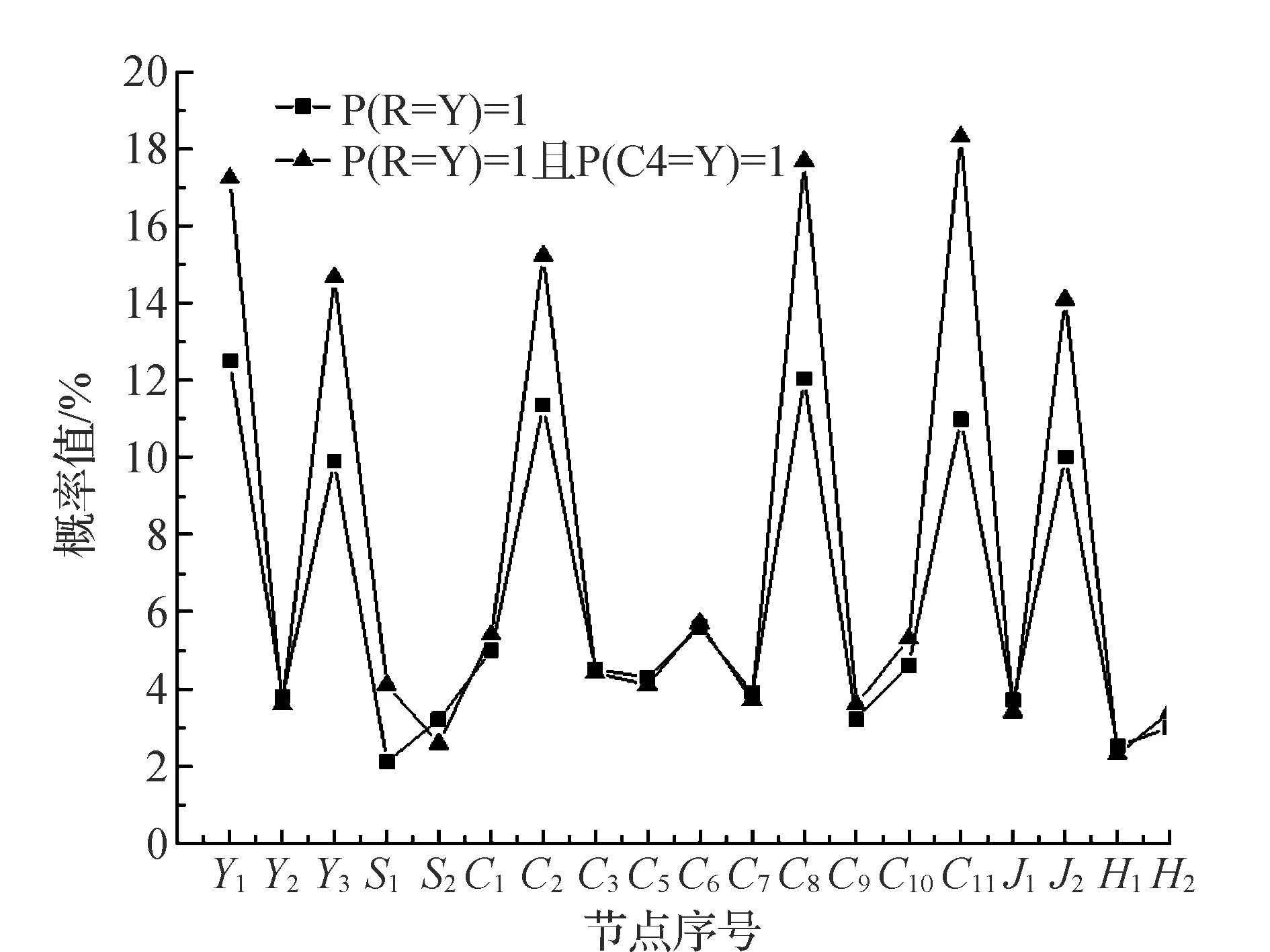
图2 风险事件诊断结果

表5 地铁轨道施工风险基本信息表

4 结 论

为提高地铁隧道施工中风险评价的准确性，完善了现有风险评估方法在处理不确定性分析方面的不足，本文运用贝叶斯定理进行风险评价。通过对贝叶斯定理的介绍，并结合具体工程案例，将研究的基于贝叶斯定理对隧道施工风险的评价方法应用到安全风险等级分析和评价中，统计分析出国内地铁轨道交通安全的20个风险因子，以此构建贝叶斯地铁轨道施工风险管理的BN拓扑结构模型，最后利用互信息法对本次事故进行了易发性评价。发现C11、C8、C2对风险事件的控制作用更强，在地铁工程建设全生命周期里，施工阶段是事故高风险阶段。