基于信道状态信息的人体复杂动作识别方法

郝占军,段 渝,党小超,曹 渊

(1.西北师范大学 计算机科学与工程学院,兰州 730070; 2.甘肃省物联网工程研究中心,兰州 730070)

0 概述

无线通信基础设施的广泛部署,促进了以基于无线通信网络的人类行为识别为核心技术的各种应用发展[1]。传统的人类行为识别需要配置可以佩戴在人体上或者部署在环境中的物理传感设备[2],如UWB、RFID和加速度传感器等,通过读取其采集的信息进行行为识别。尽管传统的行为识别方法已被普遍使用并取得了良好效果,但因其需要特定的传感器设备,使用成本较高。随着无线通信技术的发展,基于Wi-Fi的行为识别由于其在室内区域中的普遍可用性而受到越来越多的关注。由于无需穿戴传感器设备就可以自动识别人体行为,因此该技术已在现实生活中得到广泛应用,例如智能家居、远程医疗保健、校园安全、重症病人监护、老年人活跃度检测等[3]。

传统的室内人类行为检测主要依靠接收信号强度(Received Signal Strength,RSS)方法[4]。但实验结果表明,RSS方法的动作识别效果差,稳定性低。与RSS相比,信道状态信息(Channel State Information,CSI)是一种MAC层更细粒度的度量,其描述了无线信号的幅度衰减和相位移动[5],通过CSI可有效识别生命体征、基本行为以及复杂的活动[6]。例如:文献[7]通过分析CSI信号来检测心率和呼吸频率;文献[8]开发E-eyes系统来进行人体步态识别;文献[9]开发WiFi-ID系统来识别人类身份。根据识别算法和应用场景的不同,CSI人体动作识别方法可以分为基于模型的识别和基于指纹库的识别,两者最主要的区别为是否需要进行先验学习[10]。基于模型的识别方法通过接入大量的接入点(Access Point,AP)来准确识别人类行为,例如文献[11]建立的Fresnel模型,这导致了硬件成本和维护费用较高。基于指纹库的识别方法通过离线阶段训练和在线阶段识别进行模式匹配,即可实现人体动作的识别,其无需密集部署AP,甚至可以仅使用单个AP,硬件和维护成本较低且基本不会影响人类的正常生活。

目前多数CSI人类行为识别研究仅能识别简单的日常行为或者单一的人体站立蹲起姿势,在实际场景中无法有效地识别复杂的人体动作。为此,本文提出一种基于CSI的人体复杂动作识别方法Wi-KongFu。将识别过程分为离线和在线2个阶段,离线阶段采集形意拳招式的CSI数据进行训练并构建特征指纹库,在线阶段通过对采集动作数据分类并与特征指纹库匹配,得到最终识别结果。

1 相关理论

1.1 信道状态信息

Wi-Fi信号在标准协议下传输使用正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)调制方式,将数据编码到若干条不同频率载波上。本文使用文献[12]中的工具从商用Atheros网卡中提取CSI,以其时域和频域信号反映从接收机到发射机数据链路中的信道信息状态。CSI是MAC层一种细粒度的特征,其反映的信号衰减,包括折射、反射、衍射、功率的衰减等信息。

在OFDM传输系统中,一个CSI通用模型可表示为:

Y=HX+N

(1)

其中,Y、X分别代表接收信号向量和发射信号向量,H与N分代表CSI矩阵和加性高斯白噪声。由式(1)可以得出:

(2)

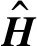
H=[H(f1),H(f2),…,H(fN)]

(3)

其中,N为不同信道带宽设置下子载波分组个数。当信道带宽设置为20 MHz时,N=30;当信道带宽设置为40 MHz时,N=114。从数据包中解析出每一个子载波的CSI频域和时域信息:

H(i)=|H(i)|ejsin∠H(i)

(4)

其中,H(i)表示第i的子载波的CSI值,|H(i)|表示第i个子载波的幅度值,∠H(i)表示第i个子载波的相位值。

1.2 巴特沃斯低通滤波器

巴特沃斯低通滤波器是一种无线冲击响应滤波器[13],若给定低通滤波器的幅频函数为H(ε),则巴特沃斯低通滤波器的幅频响应函数可以表示为:

(5)

其中,N为滤波阶数,ΩC为截止频率(单位rad/s),j为各阶系数。一个滤波器的幅频曲线包含通带,阻带以及过渡带。对于通带有:

1-δp≤|Ha(jΩ)|≤1+δp,|Ω|≤Ωp

(6)

对于阻带满足:

|Ha(jΩ)|≤δs,Ωs≤|Ω|≤∞

(7)

其中,Ωp、Ωs分别是通带和阻带的边缘频率,δs为通带内滤波器与理想滤波器幅值偏差,δp为阻带内滤波器与理想滤波器幅值偏差。

1.3 离散小波变换

小波变换被广泛应用于信号处理,其最大优势在于窗口的动态自适应性,通过调整窗口的宽度和高度,可以分析并提取出信号的有效信息。离散小波变换是对小波函数的参数作离散化处理[14-15],即对于尺度参数α,平移参数β,将ψα,β(t)中的连续变量取作整数离散形式,可得离散小波:

ψα,β(t)=2α/2ψ(2αt-k)

(8)

离散小波变换可以表示为:

Wf(α,β)=(f(t),ψα,β(t))

(9)

离散小波变换通过对参数α和参数β的调节,实现对信号的局部化处理[16]。

2 Wi-KongFu识别方法

离线阶段采集每个形意拳招式的CSI数据,以振幅作为特征值,对采集到的CSI原始数据进行预处理,利用巴特沃斯低通滤波器和离散小波变换过滤异常数据,并使用受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)进行训练分类,建立每个形意拳招式的标准指纹库。在线阶段在实验环境中采集测试人员的形意拳招式动作数据并进行预处理,使用改进深度置信网络(Deep Belief Network,DBN)对其进行进一步分类[17],然后与离线阶段建立的拳法招式标准指纹库进行实时匹配,识别具体的形意拳招式。Wi-KongFu方法识别流程如图1所示。

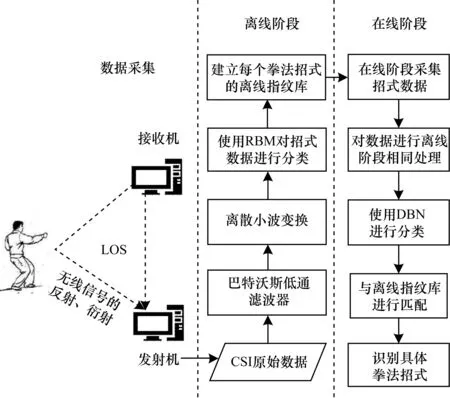
图1 Wi-KongFu方法流程Fig.1 Flowchart of Wi-KongFu method

2.1 离线数据采集

在拳法招式数据采集过程中,本文采用2×3链路,即2根发射天线和3根接收天线,每根天线可以接收56个子载波信道值。本文将形意拳动作分为8个招式来进行识别,分别为起式、崩拳、虎拳、马形拳、钻拳、横拳、劈拳以及收式。在实验过程中,分别在信号链路中做这8个拳法招式,以采集每个拳法招式的不同的CSI值。预采集的形意拳招式对应的特征值如图2所示。

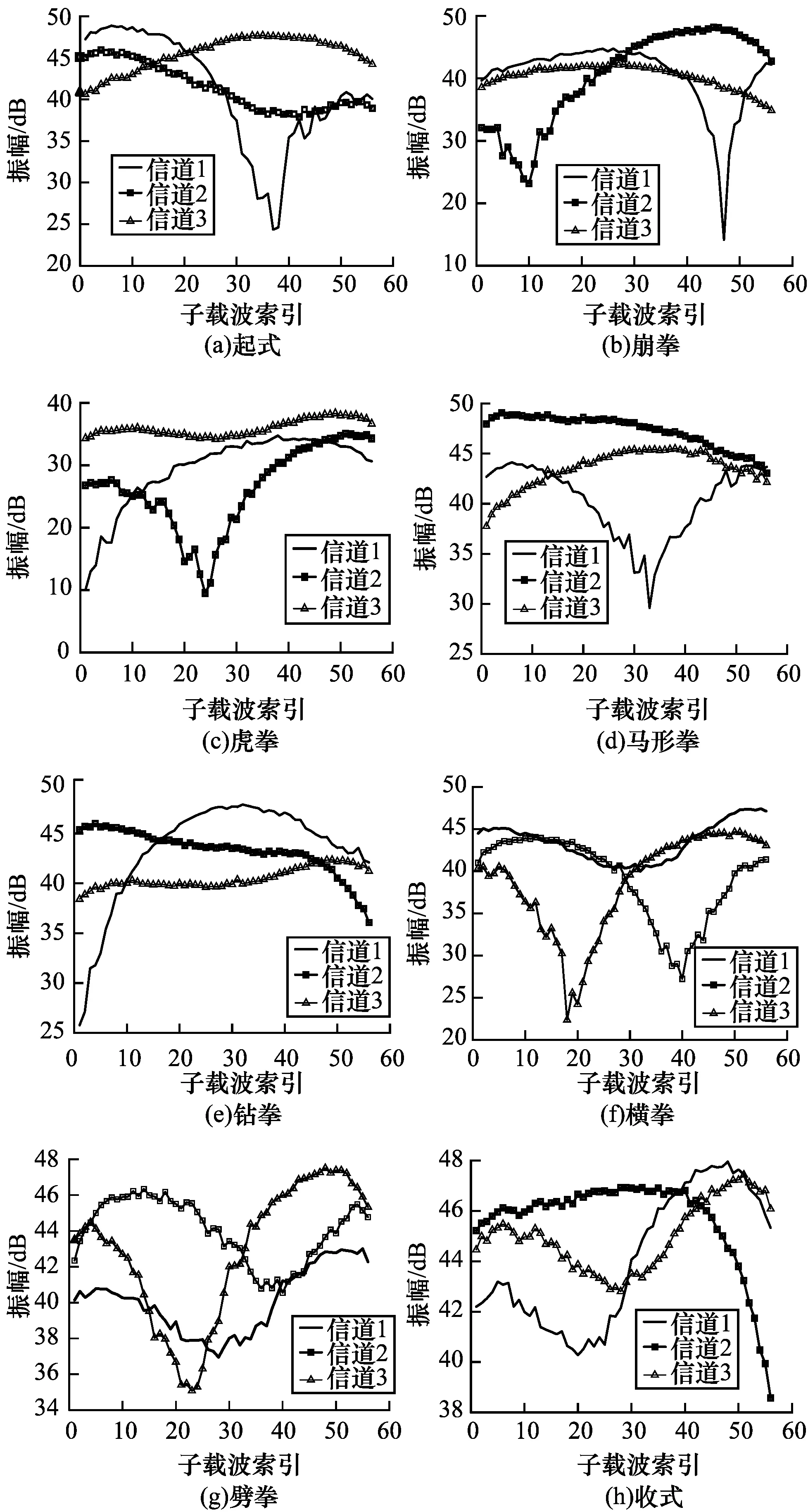
图2 形意拳招式对应的特征值Fig.2 Corresponding eigenvalues of Xing Yi Quan actions

2.2 离线数据处理

2.2.1 数据预处理

图3显示了一幅形意拳招式的原始CSI振幅图。

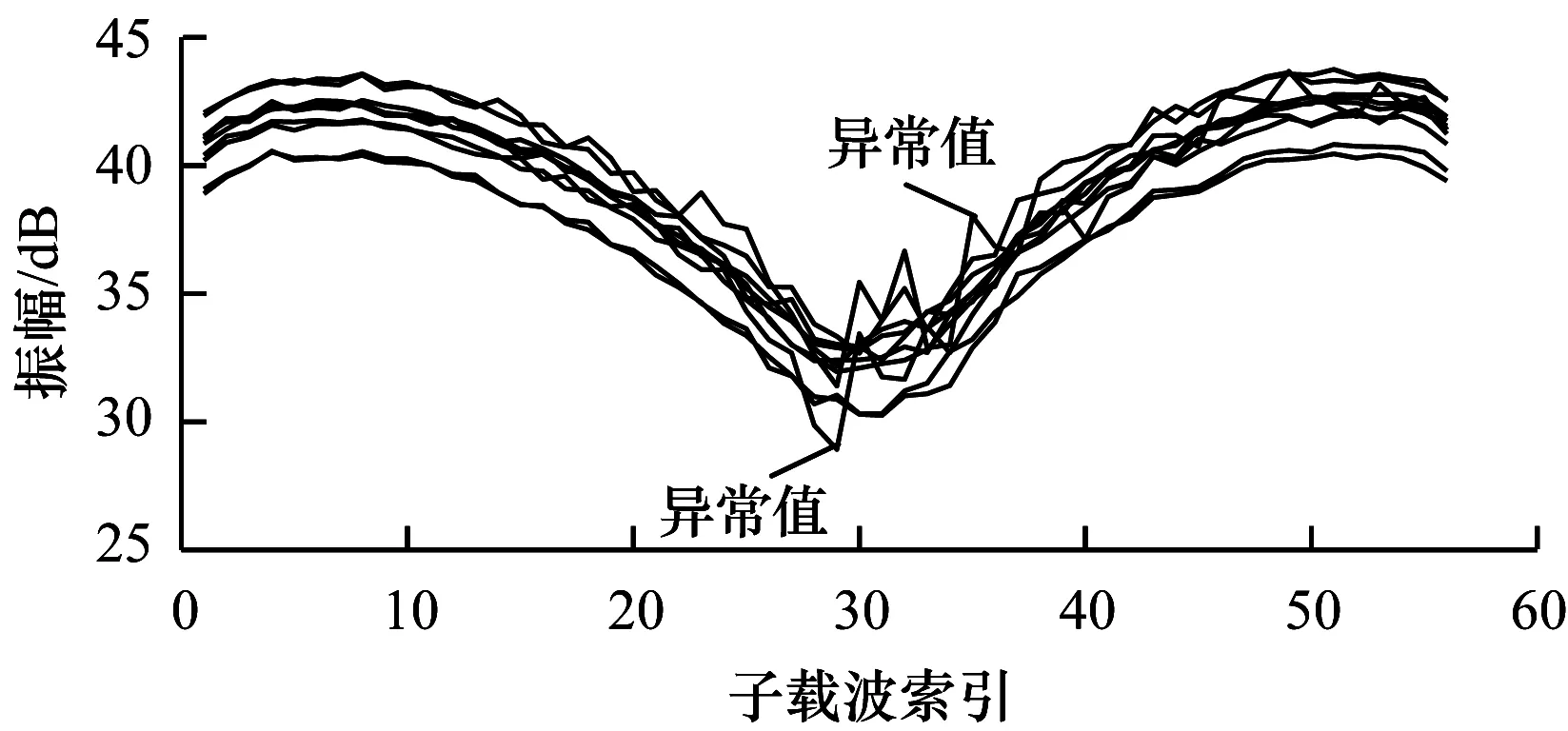
图3 原始CSI振幅图Fig.3 Original CSI amplitude map

从图3可以看出存在许多异常值。异常值的存在会导致拳法招式的识别精确度下降,为此,本文分别采用巴特沃斯低通滤波器和离散小波变换过滤异常值中的高频和低频干扰。通过数据的预处理,过滤采集数据的异常值,最大程度地保留信号特征完整性,以便建立每个形意拳招式的特征指纹信息。

通过巴特沃斯低通滤波器滤除拳法招式CSI数据中的高频异常数据,处理步骤如下:

步骤1设计巴特沃斯低通滤波器的幅频传递函数H(ε)。

步骤2设置参数η(fn,fs,fp,Rp,Rs),生成可以处理振幅数据的巴特沃斯低通滤波器。其中,fn为采样频率,fs为阻带截止频率,fp为通带截止频率,Rp为通带内波动最小衰减,Rs为阻带内最小衰减。

步骤3以形意拳招式的振幅矩阵为原始信号,利用步骤2中设计的巴特沃斯低通滤波器进行处理,过滤振幅信号的高频异常。

经巴特沃斯低通滤波器滤除异常的形意拳数据前后对比如图4所示。可以看出,CSI数据变得更加平滑,且高频异常被滤除。

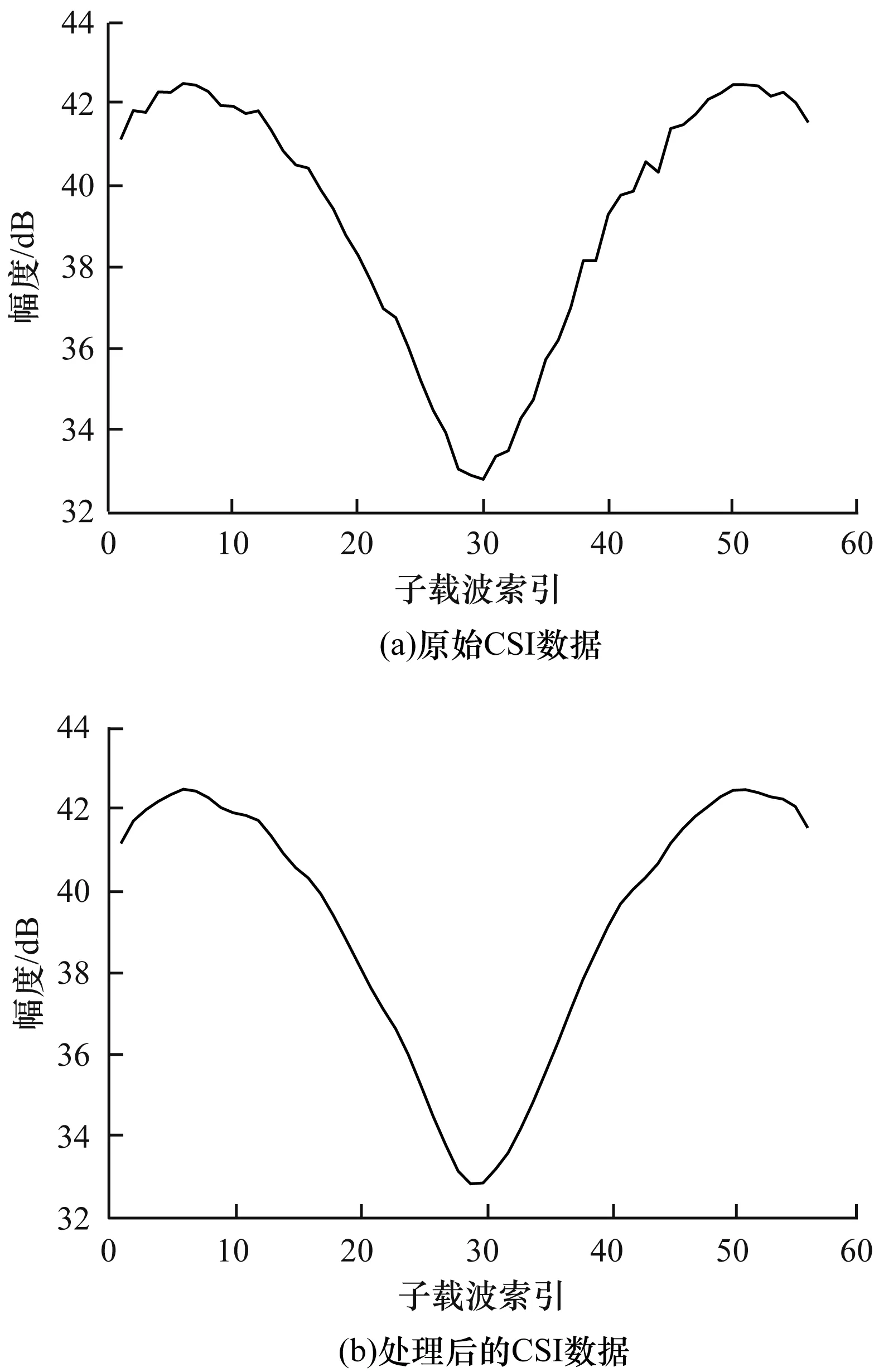
图4 巴特沃斯低通滤波器处理效果Fig.4 Processing effect of Butterworth low-pass filter

使用离散小波变换滤除CSI数据中的低频干扰数据。将拳法招式特征信息作为离散小波变换的原始输入信号,对其进行分解获得近似部分和细节部分,近似表示低频信息,细节表示高频信息[18]。通过设置函数参数ζ(x[n],g[n],h[n],↓Q),完成对拳法数据中低频信息的过滤。其中,x[n]为离散的输入信号,g[n]为低通滤波器,h[n]为高通滤波器,↓Q为降采样滤波器。经离散小波变换处理的数据如图5所示。将滤除低频异常后的CSI数据作为训练样本集,进行下一步对拳法数据的分类。

图5 离散小波变换滤除低频异常效果Fig.5 Effect of discrete wavelet transform filtering low frequency anomalies

2.2.2 形意拳招式动作分类

以上述预处理后的数据作为训练样本,使用RBM训练。假设训练集λ={λ(1),λ(2),…,λ(t)},其中,t为训练样本的个数,利用极大似然法求解RBM训练的似然函数P(v):

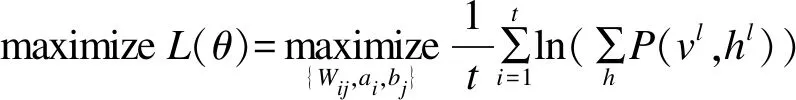
(10)

本文采用k步对比散度算法对RBM网络进行训练,即其只需要M步吉布斯采样就可以得到适合待训练样本模型的近似[19]。根据式(10),当显层数据一定时,可推导出所有隐层神经元的激活状态的概率,如式(11)所示。同理,当隐层数据一定时,也可以由式(12)推导出显层神经元的激活状态。

(11)

(12)

其中,σ(x)为神经元的非线性sigmoid激活函数,如式(13)所示。

(13)

2.2.3 离线指纹库建立

对采集的形意拳招式数据进行预处理,作为指纹信息S=(S1,S2,…,SW)T。将S作为待训练样本集,对RBM进行训练,训练过程如下:

步骤1初始化RBM,对显层神经元赋初值v0=v。

步骤2对训练样本集S进行吉布斯采样,当时间l=1,2,…,M时,进行M步的吉布斯采样。

步骤3对显层神经元数据进行吉布斯采样,并对其进行处理。可以由隐层采样显层,使用P(h(l)|v(l-1))计算出相应的vl。同理,对隐层神经元数据进行吉布斯采样,可以使用P(hl-1|vl-1)计算出hl-1。

步骤4对隐层和显层计算相应的期望值,完成训练。

通过对训练样本集的M步吉布斯采样后,系统就可以获得一个适合训练样本模型的近似采样值。与此同时,系统也可以确定显层神经元的激活状态,本文使用训练后的指纹信息记作S′=(S′1,S′2,…,S′W)T,建立每个形意拳招式动作的特征指纹库。

2.3 在线动作识别

2.3.1 在线识别

在线识别阶段使用发射机采集每个待识别动作数据,将采集到的数据发送给接收机,选取CSI数据中的振幅作为特征值。信号中的频率表示由身体运动引起的多径变化速度,幅度表示信号的能量[20],因此,通过分析信号中的幅度信息,可以得到每个形意拳招式的幅度特征,进而判别出不同的招式动作。

在线阶段识别流程如下:

步骤1在搭载Atheros网卡的接收机与发射机间采集实时形意拳招式数据。

步骤2选取形意拳招式CSI数据中的振幅作为特征值。

步骤3通过数据预处理过滤异常值。

步骤4将通过预处理的数据作为待训练的样本集,使用改进的DBN进行训练,提高分类精度。

步骤5将分类后的形意拳招式数据与离线阶段构建的形意拳招式指纹库进行实时匹配,识别测试人员的动作。

2.3.2 在线形意拳动作分类

为了更好地对在线阶段形意拳动作进行分类,本文使用改进的DBN模型对形意拳招式动作进行分类,其伪代码如下:

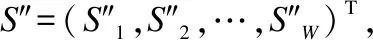
输出DBN模型以及参数θ′

//预训练阶段

//初始化DBN网络

第一个显层RBM值v(1)=v(x),对偏置a和偏置b赋初值为0,令权重参数W满足正态分布(0,0.01);θ′(W′ij,a′i,b′j)

for epoch=1,2,…,Z

for j=1,2,…,Nh

//计算隐层神经元被激活的状态:

从P(h1(j=1)|h1)中抽取均匀分布的随机值h1(j)∈{0,1};

endfor

for j=1,2,…,Nv

//计算显层神经元被激活的状态:

从P(v2(i=1)|h1)中抽取均匀分布的随机值v2(i)∈{0,1};

endfor

//微调阶段:

//使用对比散度算法更新权重参数W,偏置a、b:

a→ma+ρ(v1-v2)

b→mb+ρ(P(h1=1|v1)-P(h2=1|v2))

3 实验与结果分析

3.1 实验环境

为验证Wi-KongFu方法在实际场景中的可行性,本文采用设备为:2台台式电脑(网卡为Atheros AR9380,CPU为 Intel Core i3-4150,操作系统为Ubuntu 16.04 LTS4.1.10 Linux内核版)和5根1.5 m的外部天线。其中,一台电脑作为发射端,另一台作为接收端,分别将发射机和接收机Atheros网卡的天线触点使用外部天线接出。实验场地选择为空旷无人的大厅、走廊和实验室以对应多径效应由低到高的变化。实验环境和实验环境平面结构如图6所示。

图6 实验场地及其平面结构Fig.6 Experimental sites and the corresponding plane structures

3.2 实验设计

设置3根发射天线和2根接收天线以形成 6条传输链路。保持接收机和发射机的高度、距离以及发射机发包速率一定,在3种不同实验环境中,分别安排测试人员站在发射机和接收机中点位置做形意拳的固定招式,每个形意拳招式采集CSI数据5 000包,保存至接收机PC端,经过Wi-KongFu方法处理后,利用RBM对每个形意拳招式数据进行训练学习,建立每个形意拳招式的标准特征指纹信息。

在线识别阶段,在实验场地中,测试人员站在发射机和接收机的中间位置做任意的形意拳招式,实时采集并处理CSI数据,使用DBN进行分类,通过已建立的形意拳招式标准特征指纹库进行实时匹配,识别测试人员的形意拳具体招式。

3.3 性能分析

在离线阶段形意拳招式动作标准指纹库的建立过程中,发射机和接收机的距离、发射机的发包速率等设置对识别效果起到关键作用。

3.3.1 距离对识别性能影响

为了分析发射机和接收机之间距离对本文方法的影响,在离线指纹库构建阶段,保持其他条件不变,分别设置发射机与接收机之间距离为0.8 m、1.0 m、1.2 m、1.4 m、1.6 m、1.8 m、2.0 m,最终识别结果如图7所示。可以看出,随着发射机与接收机之间距离的增加,每个形意拳招式识别准确率基本呈现先上升后下降的趋势,当发射机与接收机距离为1.2 m时,其识别准确率最佳。

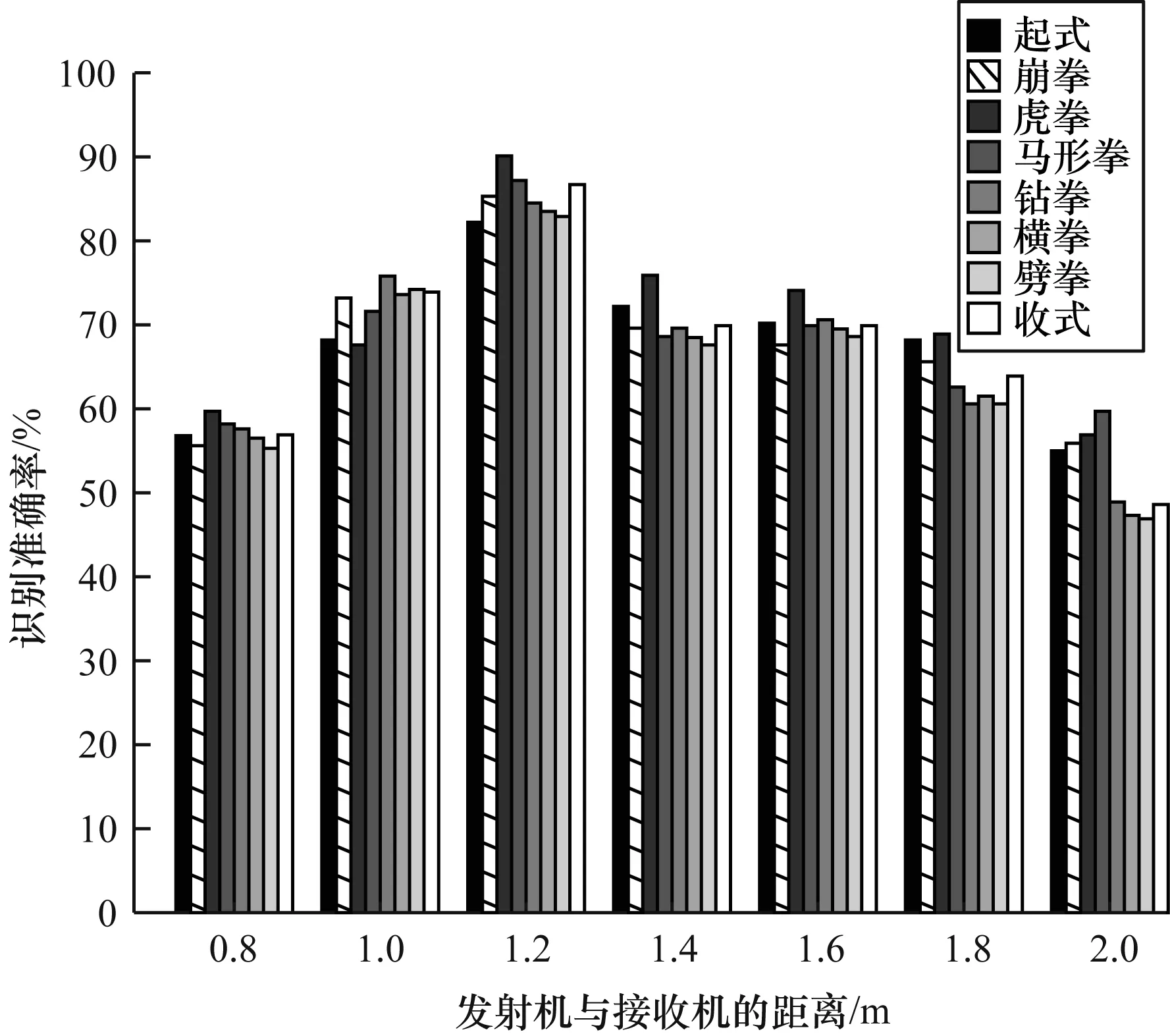
图7 发射机与接收机距离对识别效果影响Fig.7 Influence of the distance between the transmitter and the receiver on recognition effect

3.3.2 发包率对识别性能的影响

发射机的发包速率决定了相同时间内采集样本的数量以及拳法招式动作在数据链路中被采集的灵敏度。由于信号在空气中传播有一定的衰减,因此相同时间下不同发包率采集到的样本数据损失数目也不同。在其他条件一定时,本文将发包率设置为10包/s、20包/s、50包/s、100包/s,分析其对本文方法识别效果,结果如表1所示。可以看出,当发射机发包速率为10包/s时,拳法招式在数据链路中被采集的灵敏度最佳,异常值干扰最小,采集到的包数衰减最少,更能真实地反映每个不同形意拳招式对数据链路信号的影响。

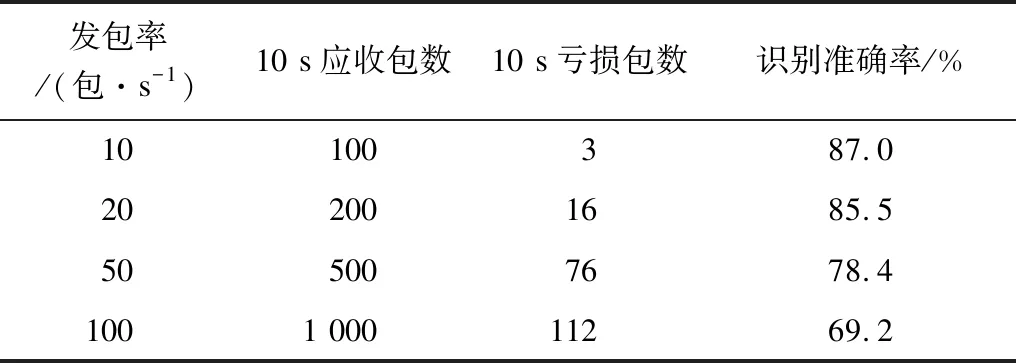
表1 发射机发包速率对识别效果的影响Table 1 Influence of packet transmitting rate on recognition effect

3.3.3 不同人员对识别性能的影响

本文选取2个测试人员做相同形意拳招式动作,来验证通过大量数据采集构建的形意拳招式标准指纹库的可用性和Wi-KongFu方法的识别效果。以形意拳起式动作为例,2个测试人员分别在发射机与接收机距离为1.2 m、发包率为10包/s的条件下,做相同的起式动作,采集数据后通过Wi-KongFu方法进行处理,实验结果如图8所示。可以看出,采集到的振幅特征值趋势近似一致,表明Wi-KongFu方法识别效果较好。

图8 测试人员对Wi-KongFu方法的影响Fig.8 Influence of testers on Wi-KongFu method

3.3.4 不同实验场地对识别性能的影响

本文根据多径效应由低到高,分别在空旷无人的大厅、走廊、实验室中进行实验,结果如图9所示。

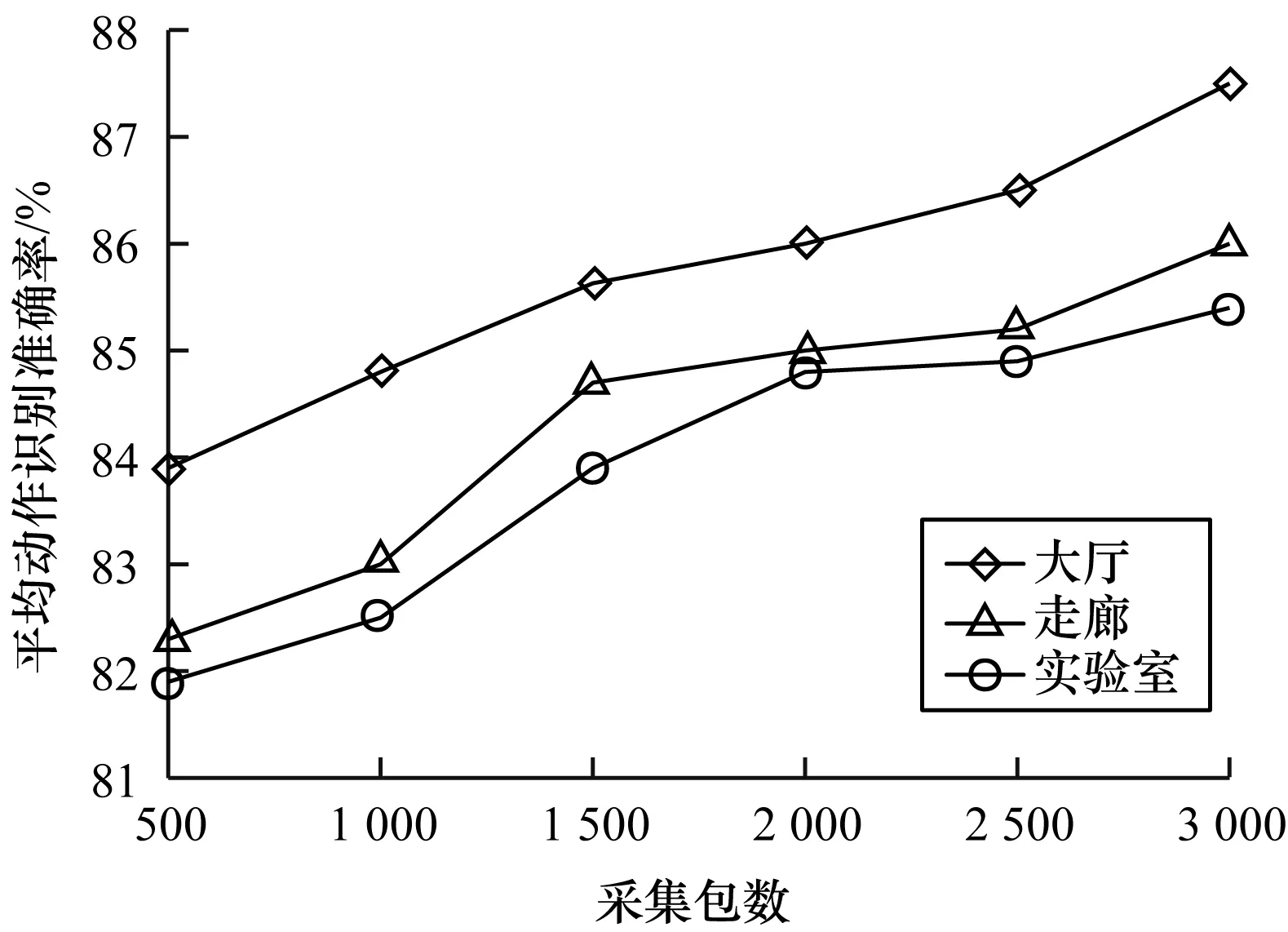
图9 3种场地的平均动作识别准确率Fig.9 Average action recognition accuracy rate at 3 different sites

可以看出,随着采集数据包数的增加,本文方法在3种场地中拳法招式的识别准确率均能达到85%以上。其中,空旷无人的大厅为识别效果最好的场地,其次是走廊,最后是实验室。这是因为实验室环境复杂,多径效应严重,大量障碍物对信号传输造成干扰,走廊中的障碍物较少,信号干扰并不严重,而空旷无人的大厅场地中几乎没有障碍物,多径效应对实验干扰很小。

3.3.5 动作识别效果分析

实验分别采集2个测试人员多次做8个形意拳招式的数据,基于每个形意拳招式的标准指纹信息进行分类,并独立验证了每个招式动作。图10通过混淆矩阵的形式,给出了形意拳招式识别的效果。可以看出,所有招式动作的识别准确率均在85%以上,起式的识别准确率达到90%,说明Wi-KongFu方法能对形意拳的8个招式动作进行有效区分。

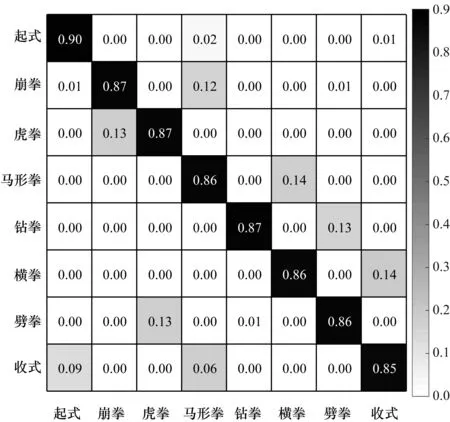
图10 8个形意拳招式动作的混淆矩阵Fig.10 Confusion matrix of 8 Xing Yi Quan actions

3.3.6 动作识别整体性能分析

为了验证Wi-KongFu方法的整体性能,本文将其与CSI-SRC、传统RSSI方法进行对比实验,评价指标为准确率。3种方法的实验结果如图11所示。

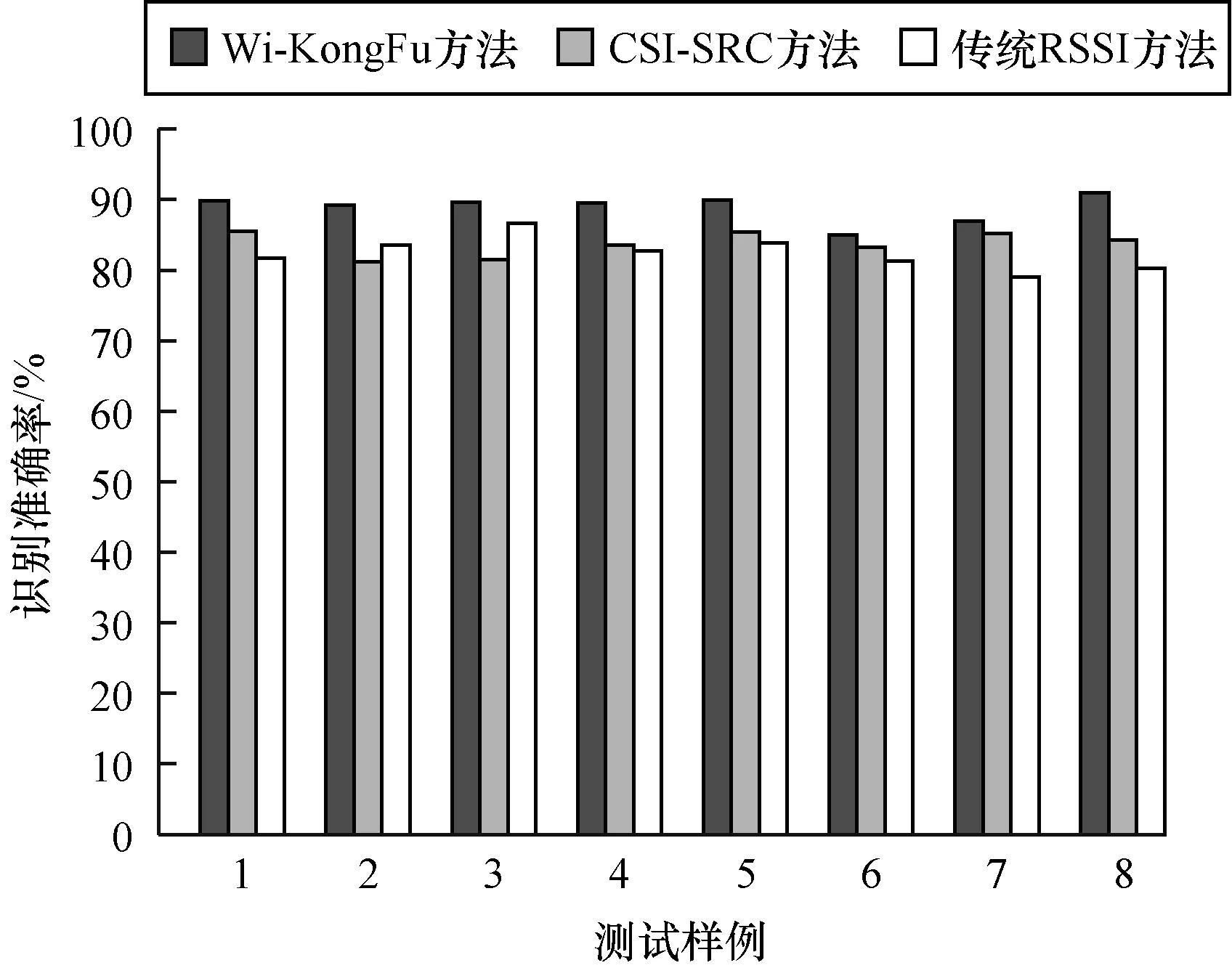
图11 3种方法准确率的比较Fig.11 Accuracy rate comparison of 3 methods

可以看出,3种方法的准确率均能达到80%以上,但相比于CSI-SRC与传统RSSI方法,Wi-KongFu方法的准确率较高且相对稳定,整体识别性能较好。

4 结束语

本文提出一种基于CSI的人体复杂动作识别方法Wi-KongFu,并以形意拳招式作为复杂动作进行验证。离线阶段采集每个形意拳招式CSI数据,结合巴特沃斯低通滤波器和离散小波变换对其预处理后,使用RBM进行训练并分类,建立标准指纹库。在线阶段使用改进的DBN方法对过滤后的实时数据进一步训练和分类,并与指纹库进行数据匹配,从而实现对不同形意拳招式的识别。实验结果表明,与CSI-SRC和传统RSSI方法相比,Wi-KongFu方法在鲁棒性和动作识别准确率方面性能均较好。后续将对该方法进行改进,进一步提高识别精度并使其能分辨更细粒度的动作。