概念漂移数据流集成分类算法综述

杜诗语,韩 萌,申明尧,张春砚,孙 蕊

(北方民族大学 计算机科学与工程学院,银川 750021)

0 概述

在信息时代,人们每时每刻都在产生海量数据,例如社交网络、交通流量和各种传感器等。数据通常以流的形式出现,数据流是随时间推移到达的潜在无界且有序的实例序列。数据流挖掘是大数据时代最重要的研究领域之一,其目标是从连续的数据流中提取出隐藏的信息。

数据流分为静态数据流和动态数据流(概念漂移数据流)。静态中的实例虽然以未知的概率分布,但以固定的来源出现。动态目标概念(实例类)或属性分布随时间演变,即概念漂移。概念漂移反映在传入的实例中,其降低了从历史训练实例中得到分类器的准确性。概念漂移问题是一个急需解决的问题,如分类器不能及时获取新知识且不能较好保存历史数据等。在现实生活中受概念漂移影响的实例有很多,如交通监控、金融诈骗检测、天气预报和医疗决策辅助等。

在对数据流分类时,根据处理数据实例的方式可以将分类算法分为基于块的算法、在线学习算法和增量学习算法等。Bagging++[1]和在线顺序极限学习机(Online Sequential Extreme Learning Machine,OS-ELM)[2]是基于块技术的算法。在线学习算法有LevBag[3]和知识最大化集成算法(Knowledge-maximized Ensemble,KME)[4]等。增量学习算法有精度更新集成算法(Accuracy Updated Ensemble,AUE)[5]和预测检测流框架[6]等。集成分类算法与概念漂移检测算法结合动态更新策略,可以对数据流进行更加精准的分类。

集成算法是数据流分类中使用最广泛的技术之一,其与单分类器相比具有更好的性能,且在实际应用程序中更容易部署,其主要优点是易于更新、适应性强、性能好。经典的集成算法有AdaBoost[7]、在线精度更新集成算法(Online Accuracy Updated Ensemble,OAUE)[8]、窗口自适应在线精度更新集成算法(Window-Adaptive Online Accuracy Updated Ensemble,WAOAUE)[9]。近年来提出的集成分类算法包括动态集成算法(Dynamic Ensemble of Ensembles,DE2)[10]、迭代提升流集成算法(Iterative Boosting Streaming,IBS)[11]、动态集成选择算法(Dynamic Ensemble Selection,DES)[12]等,在分类过程中可以得到准确率更高、鲁棒性更强的最终结果。

集成分类算法可以较好地处理概念漂移问题。经典算法有流集成算法(Streaming Ensemble Algorithm,SEA)[13]和精度加权集成算法(Accuracy Weighted Ensemble,AWE)[14]等。近年来提出的算法有基于熵的集成算法(Entropy Based Ensemble,EBE)[15]、确定性概念漂移检测算法(Deterministic Concept Drift Detection,DCDD)[16]、基于选择重采样集成算法(Selection-based Resampling Ensemble,SRE)[17]等,这些算法在处理概念漂移问题时,具有较高的分类精度及准确性。本文对概念漂移类型、概念漂移数据流集成分类算法及其关键策略和技术进行分析与研究。

1 概念漂移

数据流是随时间推移到达的潜在无界且有序的实例序列。设D={d1,d2,…,di-1,di,di+1,…}表示数据流,其中,di={ai,bi},ai是每个属性的第i个数据的值,bi是实例的类标签。数据流分类的目标是训练分类器,建立特征向量和类标签之间的映射关系。概念漂移数据流的特点是数据量无限、维数多且数据流中蕴含的概念随时间改变。为更好地解决数据流中的概念漂移问题,需了解概念漂移的特性,本节将从3个角度介绍概念漂移类型。

随着数据实例的引入,集群的结构会发生变化,导致集群中表示的概念发生变化,这种概念变化称为概念漂移。研究人员对概念漂移的深入理解是通过分析概念漂移的种类及产生原因逐步得到的。实际问题中会出现不同类型的概念漂移,例如在社会网络分析中,一个社会群体中的人在某一特定时期对某一特定事物感兴趣。兴趣的突然改变或逐渐改变,对人类来说是显而易见的。研究人员把这种情况的漂移称为真实概念漂移,认为漂移不仅因为所处环境发生变化导致,而且因为数据流的概率分布模型发生变化,并把后者的漂移称为虚拟概念漂移。真实概念漂移会改变类间的决策边界,而虚拟概念漂移会影响类间的比例,这与类间的不平衡问题有关,真实概念漂移与虚拟概念漂移分布类型如图1所示。

图1 真实概念漂移与虚拟概念漂移的分布类型

Fig.1 Distribution types of real concept drift and virtual concept drift

文献[13]指出概念漂移的具体表现为:1)类标号的先验概率P(a1),P(a2),…,P(ak)可能发生变化,其中,a为传入的数据实例,k为一条数据流中实例的最大个数;2)类标号的条件概率P(X|ai)(i=1,2,…,k)可能发生变化;3)类标号的后验概率P(ai|X)(i=1,2,…,k)可能发生变化。P(X|ai)的改变可能不会影响类标号的分布及数据源机制的产生,其被认为是虚拟概念漂移。P(ai|X)的改变是相同的实例在不同的时间戳下会存在不同的类标,其被认为是真实概念漂移。

现阶段对概念漂移的种类还没有达成统一的描述,除虚拟与真实概念漂移外,研究人员还根据概念漂移变化的速度,将概念漂移分为突变型、渐变型、重复型和增量型。突变漂移是指集群结构在短时间内发生巨大变化,类标号的分配与之前不同。渐变漂移是指概念的变化随着时间的推移而逐渐发生,变化频率低、幅度小。重复漂移是指当概念不规则或周期性重复出现时,就会出现重复漂移情况。增量漂移是指随时间推移概念发生缓慢演变的过程,该过程与渐变漂移有些类似,变化窗口会对应整个流程。基于变化速度的概念漂移分布类型如图2所示。

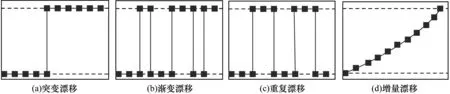
图2 基于变化速度的概念漂移分布类型

2 概念漂移集成分类算法

在数据流传输中,单分类器在对概念漂移数据流分类时会有限制,不能达到预期效果。集成分类器将基分类器组合起来,具有比单分类器更好的性能。现有算法大多只专注于一种类型的概念漂移,但是实际数据中可能会同时发生多种漂移,集成的出现可以解决此类问题,从而更好地检测出概念漂移,迅速对其做出反应,达到理想的分类效果。

2.1 突变型和渐变型概念漂移集成分类算法

突变型和渐变型概念漂移是最容易发生的两种情况。渐变比突变更具挑战性,因为其变化小,且数据分布重叠。如果变化是周期性的,则之前的变化情况可能在一段时间后重新出现。

突变漂移检测算法(Detect Abrupt Drift,DetectA)[18]是一种利用自身的主动性来检测即将发生的突变漂移机制,其优势在于主动性较好,不像大多数漂移检测程序只能检测概念漂移发生后的情况。文献[19]提出漂移检测法(Drift Detection Method,DDM),该方法在突变漂移时表现良好,但其很难发现渐变漂移。早期漂移检测法(Early Drift Detection Method,EDDM)[20]与DDM相似,只是其分析了连续错误之间的距离,而不是错误率,该算法可以改善渐变漂移的检测效果。文献[21]基于DDM提出反应漂移检测方法(Reactive Drift Detection Method,RDDM),通过添加一个显式机制来丢弃较长概念的旧实例,以减轻DDM的性能损失。该方法旨在更早地检测漂移,在预测精度上显著优于DDM,更加适合突变和渐变漂移。文献[22]提出一种由投票法、分类器组合和去除低质量分类器组成的集成分类器。在不同的数据输入条件下使用两个加权函数,可使其在决策阶段对基分类器加权,有利于提高分类器对漂移的适应性,使分类器具有更高的效率,该算法在渐变漂移和组合漂移下具有较高的精度。

SEA[13]算法对数据分类时使用新生成的基分类器替换分类中性能最弱的基分类器。该算法在所有数据的基础上构建一个决策树,可快速调整以适应突变和渐变漂移。AWE[14]算法适用于时间演化环境,根据测试数据对分类精度的期望,对集成中的分类器进行合理加权,可以较好地适应突变漂移,具有一定的预测精度。研究人员在AWE算法基础上提出了AUE[5]算法。该算法相比AWE算法不仅能选择分类器,而且可根据当前分布对分类器更新,不限制基分类器大小,适用于突变和渐变漂移。重复概念漂移算法(Recurring Concept Drifts,RCD)[23]是一种处理突变和渐变概念漂移的数据流算法。该算法使用一个可配置的多元非参数统计测试对数据样本进行比较,确定是否出现新概念或历史概念,重用并存储已有的分类器,用于数据样本的构建。EBE[15]算法将信息熵与集成相结合用于检测数据流中突变和渐变概念漂移,提高算法分类准确性。概念漂移和类不平衡在线主动学习配对集成算法(Online Active Learning Paired Ensemble for Concept Drift and Class Imbalance,OAL-DI)[24]由一个长期稳定的分类器和一个动态分类器组成,分别处理概念的突变和渐变。该算法对不同类别不平衡比的概念漂移能进行有效分类,并使用较少的真实标签,以较低的标注成本获得较高的AUC值。

适应性多元化在线提升算法(Adaptable Diversity-based Online Boosting,ADOB)[25]可以在分类器之间有效地分配实例,旨在加速分类器在概念漂移后的恢复,可以更好地适应概念漂移的发生,并且在突变和重复概念漂移的情况下特别有效。在对新实例进行分类时,ADOB分类器的误差率计算为:

(1)

(2)

(3)

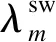
2.2 其他概念漂移集成分类算法

在概念漂移问题中,重复和增量漂移也时常发生。除了单类型的概念漂移情况,有时也会同时发生多类型漂移情况,使漂移类型变得更加复杂。

粗糙高斯朴素贝叶斯分类器(Rough Gaussian Naive Bayes Classifier,RGNBC)适用于重复型概念漂移[27]。该分类器通过自动检测重复型概念漂移对数据流进行分类,实现概念漂移的检测和分类模型的更新。朴素贝叶斯的动态特征空间集成算法(Dynamic Feature Space Ensemble of Naive Bayes,DFS-ENB)[28]对于概念重复情况可提高分类准确率。该算法在数据流动态特征空间的基础上,通过存储历史模型及概念的相似性度量,从模型库中获取与当前概念高度相关的模型进行整合更新,动态计算集成中基分类器的权重,使之前传入的数据实例得到更加有效的利用。在线顺序极值学习机集成(Ensemble of Subset Online Sequential Extreme Learning Machine,ESOS-ELM)[29]是一种计算效率较高的在线顺序极值学习机,利用循环概念先验知识的高效存储方案,适合重复漂移情况,并对突变和渐变漂移可以迅速做出反应。DCDD[16]模型具有较高的概念漂移检测精度和较好的可扩展性以及较小的虚警率和漏报率,可以有效检测突变、渐变与重复的概念漂移。在AUE算法的基础上,研究人员提出精度更新集成算法(Accuracy Updated Ensemble,AUE2)[5],该算法引入一个新的加权函数,无需对候选分类器进行交叉验证,不保留分类器缓冲区,始终更新其基分类器,适用于突变、渐变和重复漂移。

KME[4]结合了基于块和在线集成的机制,可以对不同类型的概念漂移数据流进行分类。基于分量评价和权重机制,KME漂移检测系统容易发现突变漂移,同时适用于增量型、渐变型和重复型漂移。该算法将数据流分为M个数据块,对集成成员的训练复杂度为O(Mlml),其中ml是在滑动窗口中标记的观察数。在训练阶段的时间复杂度为O(2Mlml+2Mumu+2Mly+4Muy+Mm|ZV|+Mm),其中,m是集成大小,y是当前数据块中保留的窗口数,|ZV|是验证集中带有标签的实例数量。KME算法的内存使用量为O(mbvlc+mslb+mub+4y+m+c),其中,b是VFDT的属性数,v是每个属性的最大值数,l是树中的叶子数,c是类数。SRE[17]算法将重采样操作策略和定期更新操作策略相结合,共同处理数据流分类问题。在学习非平稳数据流有效性时,SRE可以对所有类型的漂移问题和新环境快速做出反应。wt,n(xj)是实例xj(xj∈Sj)被集成选中更新的第n(1

(4)

(5)

(6)

(7)

(8)

概念漂移集成决策树算法(Ensemble Decision Trees for Concept-drifting,EDTC)[30]引入随机特征选择的3种变体实现分裂测试,并利用Hoeffding边界的不等式中指定的两个阈值区分概念漂移和噪声数据。该算法能有效地解决概念漂移数据流在噪声环境下的学习问题。Hoeffding边界可定义为:

(9)

3 集成分类学习策略

集成分类器通过加权或非加权投票方法将多个基分类器决策进行组合,共同执行分类任务,可以使整体鲁棒性更强,并且对概念漂移数据流进行有效分类。目前主流的集成学习算法是Bagging和Boosting,两种算法可在不同训练集上多次执行学习算法,并利用组合策略提升集成算法性能。

3.1 Bagging算法

Bagging根据均匀概率分布从数据集中重复抽样。给定K个样本的数据集,K次随机采样,训练K个分类器后,测试样本被指派到得票数最高的类中。样本在K次采样中不被采集的概率为(1-1/K)K,可得出初始训练集样本出现在采样集中的概率为:

(10)

Bagging++[1]通过对Bagging算法的改进,利用输入的数据块来构建新模型学习C++。该集成分类器是包含4个基分类器的异构分类器,其算法速度显著加快。Levbag[3]算法在此基础上,做出以下改进:1)增加泊松分布中的多样性值,从而增加分类器在同一实例上的训练概率;2)改变预测实例的方式、增加多样性及降低相关性,具有更好的精确度。处理漂移的多样性算法(Diversity for Dealing with Drifts,DDD)[34]通过EDDM算法来检测漂移前和漂移后的最佳集成,再使用4个具有高和低多样性的基分类器,在不同多样性水平的集成分类器中能够获得更好的分类准确性,具有更强的鲁棒性。

概率阈值Bagging算法(Probability Threshold Bagging,PT-Bagging)[35]依赖于简单的Bootstrap采样,通过阈值移动分配类标签。利用Bagging算法的优势,在阈值确定的情况下可成功应用于多类数据,但只适用于静态环境。GU[36]设计了Bagging分类树-径向基函数网络(Bagging Classification Tree-Radial Basis Function Network,BAGCT-RBFN)。该算法可成功监测信息变量,具有更高的分类准确度及更好的分类性能。基于联合进化集成算法(Association-based Evolutionary Ensemble,AEE)[37]可以提高大规模数据集下变量选择精度。该算法对数据流分类时迭代次数较少,改进了获取变量组合的集成方法,达到预期的分类精度,节省了大量计算时间。

UnderBagging[38]算法通过对多数类样本的随机欠采样创建了平衡的训练子集。该算法使用内核化ELM作为基分类器使集成稳定并具有较好的泛化性能。基于UnderBagging的内核化极限学习机算法(Under Bagging Based Kernelized ELM,UBKELM)[39]可有效处理类不平衡问题并降低成本。文献[40]提出基于SMOTE的决策树集成和具有差异化采样率的Bagging算法(Decision Tree Ensemble Based on SMOTE and Bagging with Differentiated Sampling Rates,DTE-SBD)。由于在不同的迭代次数中采用不同的采样率,因此不同DT基分类器的训练样本数也不同,DTE-SBD可以增加DT基分类器的多样性。Bagging C4.5[41]算法可以有效处理心电数据集,防止数据失真,支持医疗保健领域的临床决策,与C4.5算法相比提高了预测分类精度。

3.2 Boosting算法

Boosting算法是一个迭代过程,用于自适应改变训练样本分布,使基分类器聚焦在较难分类的样本上。Boosting替换加权数据后进行随机抽样,把若干分类器整合为一个分类器,用于提高学习算法的预测性能。与Bagging相比,Boosting可以训练出更多样化的分类器。

Boosting主要用于批处理模式,当需要随机访问数据时会受到限制,其要求整个分类训练集同时可用。文献[25]提出了ADOB算法,该算法在分类器之间可更有效地分配实例,旨在加速基分类器在概念漂移后的恢复,可以更好地适应概念漂移情况。但该算法在处理每个实例之前都要根据精度进行分类,影响了分类器的多样性分布方式。BOLE[26]算法对ADOB和OzaBoost算法进行了改进,通过弱化基分类器投票的要求和改变内部使用的漂移检测方法,提高整体精度。为适应概念漂移频繁和突变的情况,该算法提出不同策略来提高在线提升算法的准确性和集成精度,在具有更多概念漂移的数据集中效果更明显,精度增益更高。

多数在线提升算法(Online Boost-by-majority,Online BBM)[42]可以提高在线学习算法的准确性。该算法利用匹配下界,证明其在确定基分类器的数量和达到指定精度所需实例的复杂度方面具有较强的优势。渐进子空间集成学习算法(Progressive Subspace Ensemble Learning,PSEL)[43]解决了随机子空间技术的局限性。PSEL不仅适用于维数较高的数据集,而且适用于一类广泛数据集,可以得到更准确、稳定、鲁棒的分类结果。PSEL的时间复杂度TPSEL为:

TPSEL=TOE+TPSP

(11)

其中,TOE和TPSP分别表示原始集成生成和逐渐选择过程的计算成本。

TOE=O(B·l·m·logam)

(12)

TPSP=O(G(B(l·m·logam))+BlogaB)

(13)

其中,l为训练样本数量,属性数量m与分类器B的数量有关,G为迭代次数。因为G和B为常数,所以说明该算法的计算成本约为O(l·mlogam)。

AdaBoost[7]算法通过迭代过程对Boosting算法进行改进,将训练集中的所有模式分配相同权重值。在此过程中,错误分类实例的权重值增加,而正确分类实例权重值减少。AdaBoost.M1[44]算法一旦发现错误大于50%的分类器,便会停止对给定的数据实例分类,其使用预定数量的基分类器处理整个数据流,再以新的数据块更新,以便为加权投票组合提供有效的近似权重。投票提升集成算法[45]没有AdaBoost的限制,可用于构建性能更加鲁棒的集成分类器。对特定训练实例的渐变关注取决于整体分类器的预测之间的不一致程度。与标准Boosting算法相比,该算法对类标签中的噪声检测更准确且稳定。IBS算法[11]是一种基于Boosting的增量学习算法。该算法依赖于在每次获得批处理时添加适当数量的基分类器,而不像大多数批处理增量算法只添加一个基分类器,是一种有效且计算成本低的数据流分类算法。

3.3 基分类器组合

将基分类器的预测结果进行组合可以提高分类器的整体性能,常见的组合策略有平均法、投票法等。如果数据是数值型,则常用算法是平均法。投票法是组合基本学习算法的简单形式,通过对基分类器分配不同权重来选择输出结果的算法。集成结构影响投票结果,可以将投票分为排序投票、多数投票和加权投票等。其中多数投票法是假设每一个分类器对总体集成决策有相同的权重。加权投票法根据式(14)对分类器的预测进行加权。

(14)

其中,wi是ni的权重。

在加权投票中,最简单的算法是按照分类器的准确性进行分类。AWE[14]算法是利用加权投票策略挖掘概念漂移数据流的算法,但AWE只能适应潜在的概念漂移并且准确率也有待进一步提高。SEA[13]算法利用与AWE不同的修剪策略进行分类。该算法用新的基分类器替换了性能最弱的分类器,但当数据集较小且无漂移情况时,精度不高。文献[46]在AWE的基础上提出CVFDT更新集成算法(CVFDT Update Ensemble,CUE)。CUE在基分类器的权值分配、算法对数据块大小的敏感性和增加基分类器间相异度等方面进行改进,算法分类准确性高于AWE,对带有概念漂移的数据流具有较好的分类准确率和快速反应能力。在算法AWE和CUE中,通过均方误差来分配基分类器权重均方误差计算如式(15)所示。

(15)

分类器随机均方误差计算如式(16)所示。

(16)

其中,p(y)为在最新传入的数据块An中每个类所占的比例。

CUE基分类权重计算如式(17)所示。为避免分母为0的情况发生,ε通常取一个很小的正数值。

(17)

该算法的更新代价为L·O(M),其中,L是需要更新的基分类器个数,M是数据流中的数据块大小。该算法的分类代价为R·O(M),R为基分类器个数。

文献[47]提出一种单分类器高效集成技术。该技术结合剔除不相关基分类器的集成剪枝算法和加权融合模块,控制所选分类器对最终集成决策的影响,具有较低的计算复杂度。DE2是可以将基分类器从连续且非平稳的数据流中动态提取出的集成算法[10]。指数加权平均算法具有较好的学习性能和泛化能力,但该算法忽略了需要分类的查询样本周围的本地信息。误差和趋势分集驱动的集成算法(Error and Trend Diversity Driven Ensemble,ETDDE)[48]利用投票思想能有效更新集成的组合和融合参数,可以提高分类精度和准确性。基于信息熵的集成分类算法(Ensemble Classification Algorithm Based on Information Entropy,ECBE)[49]利用分类前后熵值的变化来检测概念漂移并决定基分类器的权重。权重低于预定阈值的分类器将被舍弃,从而获得较高的分类精度。动态集成选择算法(Dynamic Ensemble Selection,DES)[12]是一种动态加权算法。该算法在获得DES系统的最终输出时进行分类,可以较好地解决需要分类的数据实例被忽略的问题。

4 集成分类关键技术

在集成分类过程中,为达到理想的分类效果,会对基分类器使用多种关键技术,例如在线学习、基于块的集成技术、增量学习等。

4.1 在线学习

在线学习是一种按照顺序学习进行不断修正的模型,可以对数据流分类做出快速反应。OAUE算法基于在线学习技术,可以在固定时间和内存中,只对最后实例的窗口估计分类器误差。OAUE的训练和加权时间复杂度为O(2m),m是被选定的分量数。空间复杂度为O(kavcl(k(d+c)),其中,a是属性数,v是每个属性的最大值数,c是类数,l是树上的叶子数,k、d和c是常数。WAOAUE[9]算法在OAUE的基础上进行改进。该算法利用变化检测器提高OAUE的性能,在集成中加入一个变化检测器来确定每个候选分类器的窗口大小,适用于实时环境下的大数据挖掘。

概念漂移检测方法是一种在线学习方法,可以在数据流变化后改进基分类器,从而提高分类准确性。文献[4]结合ACE和AUE两种集成算法提出KME算法。KME算法结合了基于块的集成和在线集成的机制,可以对不同类型的概念漂移数据流进行分类。DDM[19]算法利用在线学习技术,可应用于数据实例随时间而变化的数据流。该算法提高了非平稳问题的建模算法学习能力,其应用方便,且计算效率高。RDDM[21]算法基于DDM算法,可定期重新计算由DDM负责统计的检测预警和漂移水平,且使用较小数量的实例参数化处理DDM的灵敏度损失问题,具有更高的检测精度。对概念变化的预期和动态适应算法(Anticipative and Dynamic Adaptation to Concept Change,ADACC)[50]也是一种在线学习算法。该算法使用新的二阶学习机制对动态环境做出反应。在线Biterm主题模型(Online Biterm Topic Model,BTM)[51]可以改善数据稀疏性并降低数据维度,在概念漂移检测和数据流分类中均具有较好的性能。Online BBM[42]利用在线损失最小化工具,推导出一种自适应的在线提升算法。该算法中的基分类器可以直接处理权重较高的实例,也可以对权重较低的实例拒绝采样。

4.2 基于块的集成

数据以块的形式进行传输,其中每个块包含固定数量的训练实例。算法对每个块中的实例进行多次迭代,并利用批处理算法来训练基分类器。

AdaBoost.M1[44]将资源分配网络与长期记忆相结合,该算法使用预定数量的基分类器处理整个数据流,并使用新的数据块进行逐步更新,以便为加权投票组合提供有效的近似权重。AWE[14]算法在连续的数据块上训练基分类器,并利用最新的块来评估所有基分类器,在最后的投票中选出多个最优的基分类器,达到较好的分类效果。逐渐重采样集成算法(Gradual Resampling Ensemble,GRE)[52]采用选择性重采样机制,通过重用保留的历史数据块来平衡当前的类分布,具有较高的分类精度。该算法在当前块中处理时间复杂度为O(|Pm| loga|Pm|+|Nm| loga|Nm|)。一个块在该阶段的时间复杂度为O(amlogaa),其中,a是训练块大小,m是数据流中块的数量。如果一次处理所有数据项,则需要的时间复杂度为O(|S| loga|S|),其中|S|是数据流中实例的数量。

极限学习机(Extreme Learning Machine,ELM)被广泛用于数据流集成分类问题,适合于实时反应数据。OS-ELM[2]是ELM的延伸之一,其可以通过具有固定或不同大小的块增量学习数据,而不是批量学习,无需保留旧的训练实例。在OS-ELM中,输出层的更新规则权重矩阵β可表示为:

(18)

其中,Hm+1和Tm+1对应于第(k+1)个块中的隐藏层输出矩阵和新的目标矩阵,β(m)和β(m+1)在接收到第k个和第(k+1)个块后,表示输出层权重矩阵β。Pm+1可由式(19)得出:

(19)

其中,I为单位矩阵,Pm可以迭代更新,P0表示为:

(20)

MOS-ELM算法结合了OS-ELM和WELM算法,考虑到集成学习的稳健性,可以提升在线分类器在偏斜数据流中的分类性能。文献[53]提出集成OS-ELM算法(Ensemble OS-ELM,EOS-ELM)和在线连续极端学习机的并行集成算法(Parallel Ensemble of Online Sequential Extreme Learning Machine,PEOS-ELM)。两个算法的训练精度和测试精度都优于OS-ELM,且训练速度更快,可以准确有效地学习大规模数据。在ESOS-ELM[33]算法中,每个OS-ELM网络都使用一个平衡的数据流子集进行训练。该算法提出的框架包括表示短期记忆的主要集成,在平稳和非平稳环境下都能有效解决类不平衡问题。

4.3 增量学习

增量学习是指一个学习体系不断地从新样本数据中学习知识。增量学习技术适用于数据流中实例依次到达且能够从新的数据中不断学习的情况。

在集成分类算法中有很多算法应用了增量学习技术,除了Bagging++和LevBag算法采用增量学习技术外,还有在线顺序极端学习机OS-ELM支持增量学习,其提供了一种分析增量数据的方法。IDS-ELM[54]是一种用于数据流分类的快速增量极值学习机算法。该算法将ELMS作为基分类器,自适应地确定隐层神经元的数目,并从一系列函数中随机选取激活函数,以提高算法综合性能。

EDTC[30]是一种基于集成决策树的概念漂移数据流增量算法。与其他随机决策树不同,该算法提出了3种不同的随机特征选择方法来确定树的增量生长中的切点,其是一种利用循环概念先验知识的高效存储方案,具有较高的分类预测精度。预测检测流框架[6]是一种新的处理对抗性概念漂移的框架。该框架通过对概念进行预先考虑,在动态对抗性概念领域具有一定优势。该框架作为一种有限内存的增量算法被用于处理不平衡和标记稀疏的数据流。IBS算法[11]能够处理数据流环境中的分类任务。该算法随着时间的推移对模型进行改进,根据当前准确度自动调整基分类器,并结合批量增量算法的特点,提高了模型灵活性及分类性能。

AUE[5]算法使用最近块中的观察值增量地更新历史数据块。该算法不限制基分类器的大小,不使用任何窗口。OAUE[8]是在AUE的基础上提出的一种增量算法。该算法在每次观测后对基分类器进行训练和加权,基分类器的权重与恒定时间和内存中的误差相关。AUE2[5]算法结合了块集成算法中AWE算法和Hoeffding树的增量特性,并对AUE算法进行了改进。目标是保留基分类器的简单模式,并对基于块的算法特征预测值进行加权。该算法不仅有较高的分类精度,还有较低的内存消耗。AWE、AUE和AUE2算法的均方误差和随机均方误差可由式(15)、式(16)得出,但其基分类权重不同,如式(21)～式(23)所示。

(21)

(22)

(23)

其中,ε为大于0的常数。

5 下一步研究方向

虽然现有数据流集成分类算法大多可以有效地解决分类问题,但研究人员仍有一些问题亟待解决,例如集成基分类器的动态更新、集成基分类器的加权组合、多类型概念漂移的快速检测以及复杂数据流类型的灵活处理等。笔者将对这些问题进行分析并作为本文下一步的主要研究方向。

1)集成基分类器的动态更新

在现实生活中,需要结合实际情况选择合适的算法和数据预处理方式,从而达到较好的分类效果。在处理数据流时,现今主流方法是集成分类。虽然集成分类算法在处理数据流分类问题时被广泛应用,但是仍然有很多问题尚待解决。如何在集成分类算法中实现对基分类器的动态更新已成为专家们十分关注的问题。随着新数据实例的传入,集成中分类性能较弱的基分类器将由新数据实例训练出的基分类器替换,但是对于界定集成中基分类器准确性的边界值还没有得到专家们的一致确定。因此,本文将把获得一个理想的分类错误边界值作为研究重点,利用此错误边界值将集成中性能较差的基分类器自动淘汰,并且加入新的基分类器实现集成的动态更新。

2)集成基分类器的加权组合

现有的集成分类器大多是以空间换时间,在对数据流分类时虽然在时间效率上得到了提升,但存在较高的内存消耗。通过合理组合多种算法,可以正确预测难以分类实例的类标签,从而减少计算的操作次数和运行的内存空间。其主要难点是如何对基分类器添加合适的加权策略,使基分类器可以更加合理地组合,从而提高分类器的整体性能。在下一步的研究中,笔者拟利用加权投票方法和Boosting策略对基分类器权重进行重新加权,使得构建的集成分类器具有较高的分类精度与计算效率,以及较低的内存消耗。

3)多类型概念漂移的快速检测

随着科技的发展,数据量呈爆炸式增长,产生了大量的数据。海量数据蕴含较多有益信息的同时,也使数据流类型变得更加复杂。数据流在传输过程中可能会同时产生多种漂移类型,例如突变与增量、全部漂移类型同时出现等更加复杂的情况。目前的技术仍有很多限制,研究人员依然有很多问题亟需解决,例如需进一步研究可以直接处理概念漂移问题的特征和实例选择方法[55]。在对概念漂移的集成算法进行整理时,发现同时针对全部漂移问题的算法几乎不存在,且算法会受到数据类别的限制。在下一步的研究中,笔者拟设计一个集成分类算法,使其既可以针对所有类型的概念漂移,又可以快速检测概念漂移。

4)复杂数据流类型的灵活处理

在数据流传输过程中需解决概念漂移、复杂数据流类型等问题。复杂的数据流类型包括类不平衡、维度高、错误分类成本高及数据延迟等。数据通常展现出高维问题和类不平衡的双重特点[56]。一般把数据流中类的不平衡问题称为数据集不平衡问题,其体现在样本的数量差异较大[57]。在复杂的数据流中,每一种类型都引起了研究人员的广泛关注。在下一步的研究中,笔者拟设计一个高性能算法及用于测试流的算法框架,使其对复杂动态的数据流类型可以做出快速反应并加以处理。

6 结束语

本文介绍突变型、渐变型、重复型和增量型概念漂移,阐述国内外概念漂移集成分类算法的研究现状,同时分析Bagging、Boosting、基分类器组合、在线学习、基于块的集成和增量学习等关键策略与技术。下一步将针对集成基分类器的动态更新与加权组合、多类型概念漂移的快速检测以及复杂数据流类型的灵活处理展开研究,设计新的集成分类算法以应对日益复杂的数据流环境。