借图形变换 探作图问题
2020-01-15张磊
张磊

[摘 要]翻折、平移、旋转与缩放这四种图形的运动,都是图形变换.图形变换的作图包括轴对称作图、平移作图、旋转作图与位似作图.探析图形变换中的作图问题,可以让学生熟悉各种类型的作图方法,明白各类作图的原理;可以培养学生的动手操作能力,让学生直观感受图形变化后位置关系和数量关系的变化,在图形变换的新情境问题中游刃有余.
[关键词]初中数学;图形变换;作图问题
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2020)29-0029-02
翻折、平移、旋转与缩放这四种图形的运动都是图形变换.图形变换的引入,使图形运动进入数学课程,要求学生从图形运动的角度看全等三角形、平行四边形、圆等几何图形,由过去的静态几何转变为动态几何.在图形变换里,不仅学习了图形变换的概念、性质与应用,还学习了图形变换的作图,包括轴对称作图、平移作图、旋转作图与位似作图.学生由已知图形作出关于某一直线或某一点的变换图形,能直观感受图形变化后位置关系和数量关系的变化,从而在图形变换的新情境问题中游刃有余.
一、轴对称作图
由已知图形与直线,如何作已知图形关于此直线对称的图形呢?第一步,找出图形中的关键点;第二步,过关键点作对称轴的垂线;第三步,延长垂线,在垂线的另一端取相等的线段,得到对应点;第四步,其他关键点的对应点以此类推,顺次联结各点的对应点.轴对称作图的类型包括在网格图里作已知图形的轴对称图形.在既定图形里以某边为对称轴作轴对称图形;在平面内作已知图形的轴对称图形.
(1)在图1格点中找一点E,由A、B、C、E四点构成的四边形,如果是轴对称图形,那么符合题意的图形有多少个?并写出点E的坐标以及四边形的面积;
评注:作轴对称图形重要的是找对称轴,对称轴可以是水平的、竖直的,也可以是倾斜的,本题的两条对称轴就是一水平一竖直.在已知直线上确定一点,使入射角等于反射角,方法就是找其中一个点的对称点,将另一点与对称点连成直线,所作直线与原始直线有一个交点,这个交点就是求作的点.
二、平移作图
平移作图的一般步骤是:(1)找出图形中的关键点;(2)经过关键点作直线,这条直线要与已知线段平行;(3)在平行线上截取平移距离的长度,得到对应点;(4)顺次联结各对应点得到的图形就是所求作的图形.平移作图的类型包括在网格图中平移作图,在既定图形里平移图形中的一部分,在平面内按指定的方向和距离平移作图,等等.
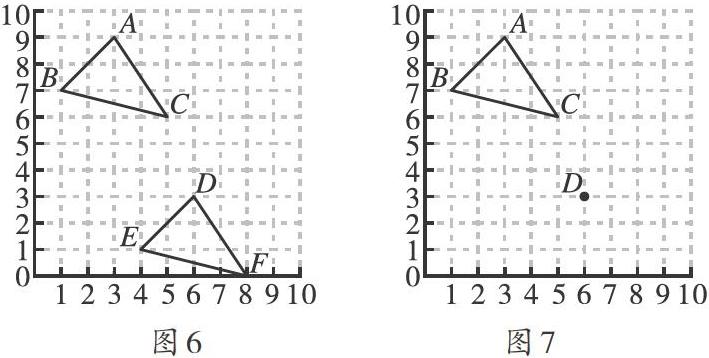
[例2]如图6,三角形ABC可通过平移得到三角形DEF,此时点A落在点D.
(1)请描述三角形ABC经过两次平移后得到三角形DEF的过程.
(2)平移三角形ABC使点B落在点D,在图7中作出平移后的三角形.
分析:(1)先沿水平方向平移再沿竖直方向平移;或者先沿竖直方向平移再沿水平方向平移.△ABC经过两次平移后得到△DEF的过程为第一步向右平移,第二步向下平移,平移的单位分别为3个和6个单位长度;
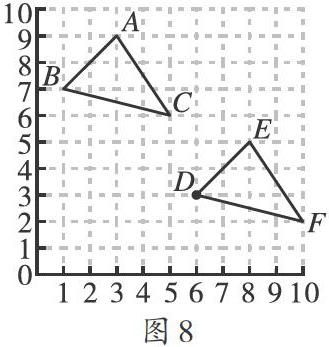
(2)根据点B的对应点是点D,得到平移的方法,再依据平移方法将点A、C平移.如图8所示.
评注:在网格里作图,要充分利用网格里的水平线与竖直线所指示的方向,利用每个小正方形的边长是1的距离,数一数格数就可以确定距离.题中显示了平移作图的两种考法,一是已知平移作图的结果,确定平移的方法;二是已知其中一点平移后的对应点,观察得到平移方法,然后平移图形.
三、旋转作图
旋转作图的一般步骤是:(1)找出图形中的关键点;(2)联结关键点与旋转中心;(3)将连线按要求的方向与角度绕中心旋轉一定的角度;(4)在连线上截取相等的线段,得到对应点;(5)顺次联结各对应点得到的图形就是所求作的图形.
评注:从这里可以看出,旋转与平移的关系,即一次旋转加一次平移相当于一次旋转.轴对称、平移、旋转之间的相互关系还包括如果对称轴互相平行,那么两次轴对称相当于一次平移;如果对称轴相交于一点,那么两次轴对称相当于一次旋转.
图形变换的作图还包括位似作图,即将一个图形放大或缩小,它要求根据相似图形对应边成比例,在经过关键点与位似中心的直线上截取几倍或几分之一的线段.在图形变换作图中,一方面考查了学生的动手操作能力,另一方面也考查了图形变换的性质,因为图形变换的性质是图形变换作图的依据.熟悉各种类型的作图方法,明白各类作图的原理,才能让学生在图形变换的新情境问题中游刃有余.
[ 参 考 文 献 ]
[1] 吴志鹏,陈玉兰.快速作图的四种策略[J].河北理科教学研究,2018(3):27-29+45.
[2] 张安军.基于等边三角形的尺规作图下“图形变换”的复习[J].数学教学,2018(3):14-16.
[3] 解荣兰. 初中生数学作图能力的研究[D].济南:山东师范大学,2017.
[4] 仇玉祥.透视中考 聚焦网格 巧妙作图[J].新高考(升学考试),2014(2):48-50.
(责任编辑 黄桂坚)