矿用液压安全联轴器的接触及转矩特性
2020-01-15廉自生2李小莉2
2 廉自生2 王 铁 李小莉2
(1.太原理工大学机械与运载工程学院, 山西太原 030024; 2.太原理工大学煤矿综采装备山西省重点实验室, 山西太原 030024)
引言
液压安全联轴器在国外已广泛用于轧机、破碎机、涡轮设备、船舶推进、高速列车等大型设备上。国内许多厂家及科研院所也相继研发出了这种安全联轴器,并出台了相应的国家标准,武钢及宝钢的进口设备上已经采用。煤炭行业中,国外的企业使用比较多,在JOY等公司生产的刮板输送机及带式输送机上有良好的应用。目前国内的煤矿使用不多,山西华润大宁能源有限公司的刮板输送机上已安装使用,效果良好。液压安全联轴器打滑转矩准确,过载响应迅速,但是,目前液压安全联轴器的打滑转矩和内腔压力关系的标定主要依靠实际测试,准确计算接触特性和转矩特性对液压安全联轴器的选型设计非常重要。
张小燕等[1]以弹性力学中的空间轴对称问题和圆柱壳体问题为理论基础,给出了薄壁圆筒问题的变形和应力计算公式;ELISHAKOFF等[2-3]对比了三种不同Timoshenko-Ehrenfest理论在弹性地基梁上的应用,指出了每种理论在自由振动的条件下的优缺点,并分析了不同边界条件的影响;杨成永等[4]建立了弹性地基梁对称问题的数学模型,推导了求解弹性地基梁挠度的傅里叶级数系数的线性方程组,提出了脱空范围的迭代步骤;李静等[5]建立了弹性地基一般梁挠度控制方程,求解得到了挠度方程解析通解;李顺群等[6]给出了在任意分布荷载作用下弹性地基梁的一种解答,该解答可以解决多种荷载类型作用下的弹性地基梁问题;王新杰等[7]结合过盈配合及设计要求,利用响应面法对缩套式超高压缸体进行优化设计;BERTOCCHI等[8]提出了一种针对轴在扭转作用下的部分滑移问题的求解方法,解决了由干涉耦合引起的接触压力问题;胡前茅等[9]将活塞唇边简化为厚壁圆筒模型,推导出活塞唇边的变形关系式,实现了变间隙密封液压缸密封间隙量的计算;DWYER-JOYCEA等[10]提供了一种可行的现场测量过盈配合接触面积和压力分布的方案;RADI等[11]以分布弹簧连接的两根弹性Timoshenko梁为模型,确定了轴轮毂初始脱离时弯曲力偶的取值;WANG等[12]建立了一种精确的分析方法来预测线弹性假设下过盈配合的压合曲线;滕瑞静等[13]提出了一种以接触边缘最大应力为优化目标的圆柱面过盈连接设计的BP神经网络动态调整算法。
综合分析,近年来有关圆柱面接触文献,研究主要集中于厚壁圆筒过盈连接问题,但是液压安全联轴器内壁形状为薄壁圆筒,且内外圆柱面是由间隙配合通过内壁的弹性变形而发生接触的。本研究对矿用液压安全联轴器的结构、工作原理、接触特性分别进行阐述,将空心缸套内壁简化为弹性地基梁,应用克雷洛夫函数法分别求解非完全接触长度和接触压力与内腔压力的关系,进而得出打滑转矩计算方法,并对液压安全联轴器的接触特性和转矩特性进行了分析与预测。
1 液压安全联轴器结构及工作原理
图1为液压安全联轴器结构示意图,液压安全联轴器包括传动轴和空心缸套,二者可以通过法兰分别和传动链前后部件相连。空心缸套内有一圈和其同轴的圆柱形空腔,可承受100 MPa高压。
通过手动高压油泵将压力油注入圆柱形空腔内,特殊材料制成的空心缸套内壁发生弹性变形, 向传动轴收缩贴紧,发生接触和摩擦。在摩擦力的作用下空心缸套与传动轴可以传递一定限度以内的转矩。通过手动高压油泵来控制内腔压力的大小,然后拧紧安全管,使压力油密封在空心缸套之中。工作过程中,当工作转矩超过最大静摩擦转矩时,则空心缸套与传动轴之间产生相对运动(即打滑),起到安全保护功能。一旦峰值转矩结束,由于摩擦副材料的动静摩擦系数的差值较小,当负载转矩小于轴和缸套之间的动摩擦转矩时,联轴器会快速恢复到同步转动的工作状态中。通过设定内腔压力的大小,可以控制联轴器传递的最大转矩(打滑转矩)。
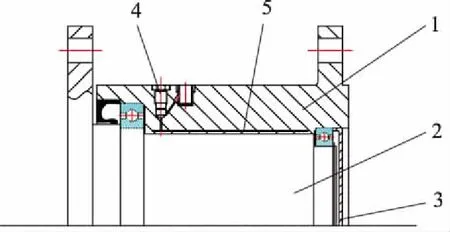
1.空心缸套 2.传动轴 3.轴承盖 4.安全销 5.内腔图1 液压安全联轴器结构
2 摩擦面接触特性
打滑转矩准确与否是衡量安全联轴器最重要的指标。为此,必须确定给定内腔压力下液压安全联轴器传递转矩的能力。
图2为液压安全联轴器尺寸参数,空心缸套内腔压力为p,传动轴直径为d,空心缸套内壁厚为h。内腔压力p为0时,初始间隙为δ,空心缸套内壁平均半径为R,空心缸套长度为l,非完全作用长度为Xa,非完全接触长度为Xb。
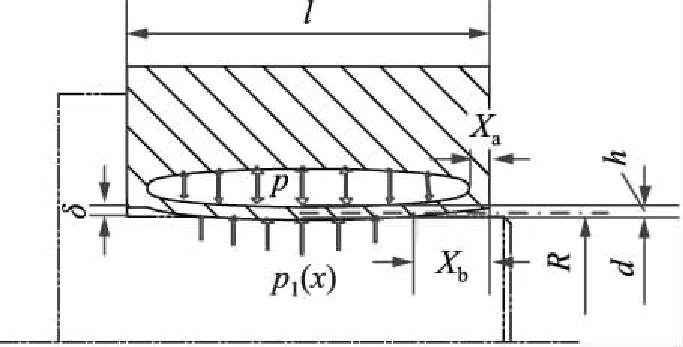
图2 液压安全联轴器尺寸参数
根据摩擦学理论,考虑到空心缸套的对称性,假设坐标原点在空心缸套内壁中点,通过对压力p1(x)在0~(l/2-Xb)上的积分可得出传递转矩的表达式为:
(1)
式中,f—— 摩擦系数
p1(x) —— 接触压力,MPa
所以,求解打滑转矩的关键是非完全接触长度Xb及接触压力p1(x)分布的求解。
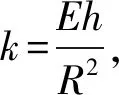
其中,E为材料的弹性模量,MPa;μ为泊松比。
梁所受外载荷为内腔压力p以及接触压力p1(x),两端截面所受的弯矩Ml/2=0,剪力Ql/2=0。梁所受载荷如图3所示。
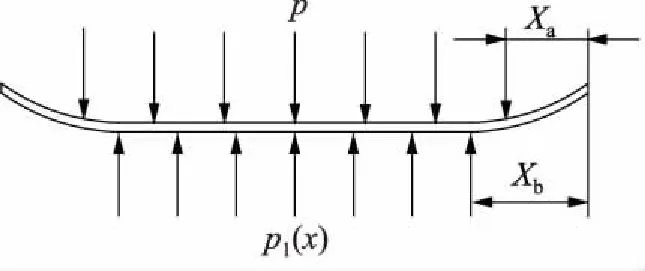
图3 弹性地基梁所受外载荷
梁的弹性变形由内腔压力造成的变形和接触压力所造成的变形叠加而成,如图4所示。
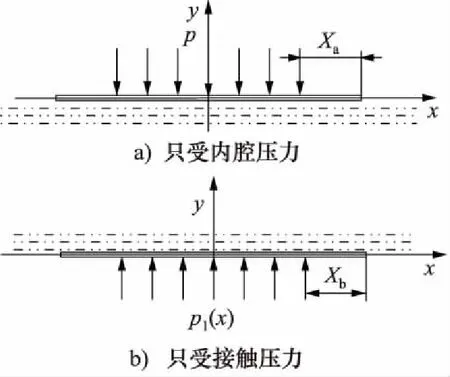
图4 内腔压力和接触压力分别单独作用
2.1 内腔压力单独作用

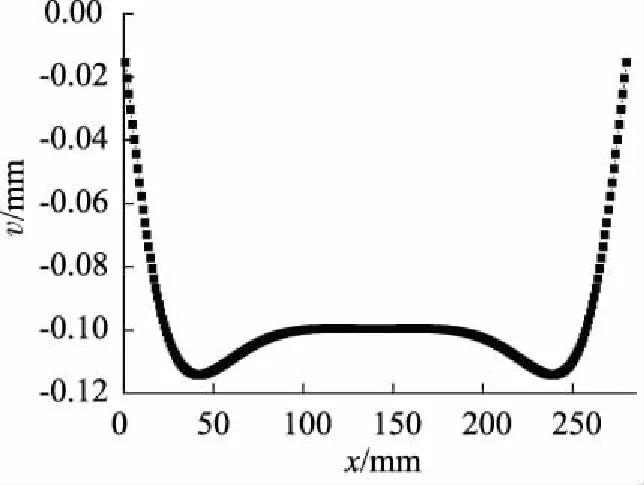
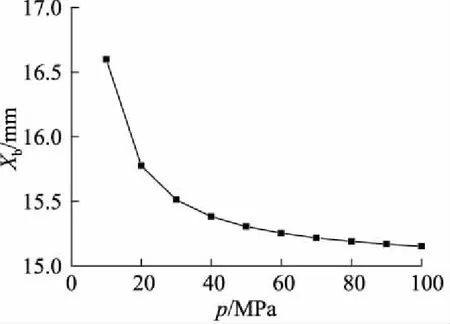
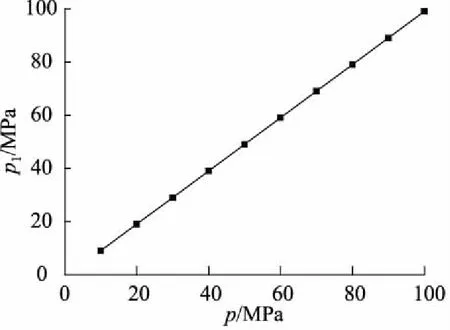
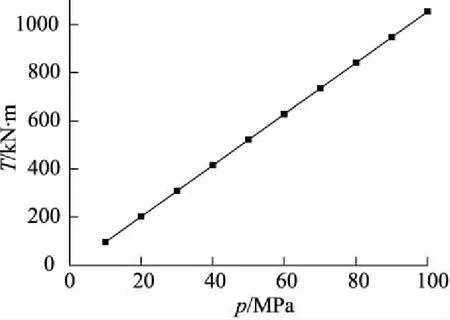
在0 (2) 应用克雷洛夫函数法,得其挠度为: (3) 其中: Y1(βx)=chβxcosβx (4) 因为变形和内力都关于梁中点对称,故有: x=0时,θ′0=Q′0=0 则梁在0 (5) 同理,梁在(l/2-Xa) (6) 两段内挠度v′的表达式统一写为: (7) 弯矩为: (8) 剪力为: (9) M′l/2=4β2EIv′0Y3(α)+M′0Y1(α)- (10) Q′l/2=4β3EIv′0Y2(α)-4βM′0Y4(α)- (11) 其中,α=βl/2。 两式联立解得: (12) (13) 所以由式(7)可得: (14) 假定接触压力为均布载荷p1,非完全接触长度为Xb,受力如图4b所示,同样有: x=0时,θ″0=Q″0=0 则梁的挠度为: (15) 该情况下有4个未知数,即v″0,M″0,p1、Xb,可以列出4个方程: 根据边界条件M″l/2=0,Q″l/2=0,有: M″l/2=4β2EIv″0Y3(α)+M″0Y1(α)- (16) Q″l/2=4β3EIv″0Y2(α)-4βM″0Y4(α)- (17) 在x=0,x=l/2-Xb两点处都有v″+v′=-δ,于是: v″0+v′0+δ=v″0+ (18) v″l/2-Xb+v′l/2-Xb+δ=v″0Y1[β(l/2-Xb)]- (19) 利用数学软件MATLAB计算这个4元非线性方程组,梁的材料为铝青铜,弹性模量E=110000 MPa,泊松比μ=0.335,尺寸条件为h=4 mm,R=222 mm,l=280 mm,δ=0.1 mm,Xa=15 mm。 梁的总挠度为内腔压力及接触压力分别单独作用时挠度的叠加,即v=v′+v″,如图5所示。 图5 弹性地基梁挠度 内壁两端变形几乎为0,靠近中间变形急剧增大,在内外圆柱面刚发生接触处变形最大,再靠近中间变形逐渐减小,在中心区域变形减小到初始间隙大小。这是由于加压后两圆柱面抱紧的状态近似过盈配合,中心区域接触压力基本均匀,接触边缘有应力集中。由于包容件外径很小(只比接触面直径大2 h),所以接触边缘的应力集中效应不显著,而且应力集中区域轴向长度很小,所以接触边缘应力集中对打滑转矩的影响可以忽略。图中为不考虑应力集中,假定接触压力均布的情况,因而在接触边缘的挠度小于-δ,若考虑应力集中,接触边缘挠度会更加接近-δ。 同理,可以求得不同内腔压力p下的非完全接触长度(如图6所示)及接触压力(如图7所示)。 图6 非完全接触长度 图7 接触压力 内腔压力越大,非完全接触长度越小,非完全接触长度在内腔压力较小时变化剧烈,随着内腔压力的增大,非完全接触长度变化趋于平缓。这是由于内腔压力较小时,内外圆柱面刚接触,接触面积增加很快,内腔压力增大到40 MPa以上后,内外圆柱面几乎已经完全接触,接触面积增加空间不大,因而趋于平缓。 由图可知,内腔压力越大,接触压力越大, 接触压力与内腔压力基本相等。这是由于空心缸套内壁很薄,内腔压力几乎全部传递到接触面上。 将接触压力及非完全接触长度的理论计算结果带入式(1)可以求得不同内腔压力p下的打滑转矩T,得出压力转矩校准图如图8所示。 由图8可知,液压安全联轴器在前文所述结构尺寸及材料条件下,打滑转矩T和内腔压力p为线性关系,这与文献[14]中试验所绘压力与滑动转矩关系图相一致。 图8 打滑转矩特性 因此,对矿用液压安全联轴器接触特性和转矩特性分析,得出如下结论: (1) 内腔压力越大,非完全接触长度越小,接触面积越大,但是由于液压安全联轴器两圆柱面间间隙很小,所以内腔压力较大时,对接触面积的影响不大;又因为壁厚很薄,所以接触压力与内腔压力成正比,因而打滑转矩和内腔压力近似线性关系; (2) 将液压安全联轴器圆柱形内壁简化为弹性地基梁,应用克雷洛夫函数法分别求解其单独受内腔压力和接触压力时的情况,确定了非完全接触长度及接触压力与内腔压力的关系,建立了接触特性和转矩特性的计算方程,可以对液压安全联轴器的打滑转矩进行分析和预测。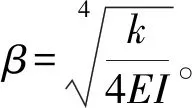
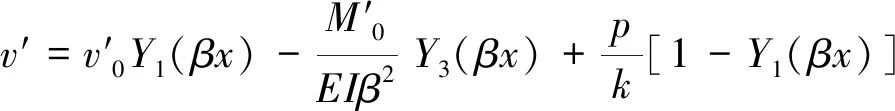
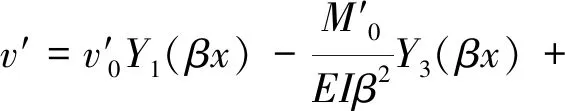
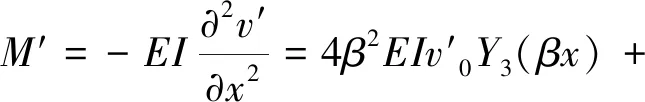

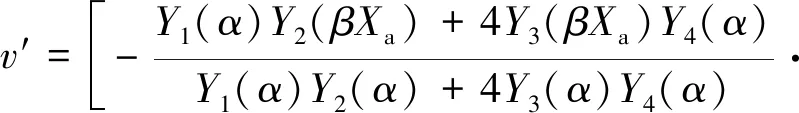
2.2 接触压力单独作用

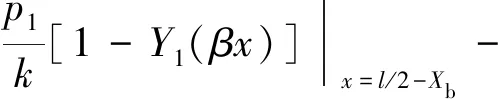


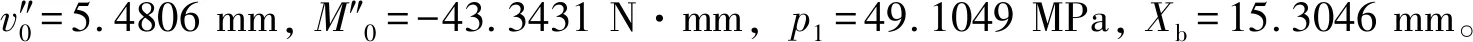
3 结果分析
4 结论
