正流量液压泵动静态特性分析与仿真建模

2020-01-1523

液压与气动 2020年1期

(1.燕山大学机械工程学院，河北秦皇岛 066004；2. 燕山大学河北省重型机械流体动力传输与控制实验室，河北秦皇岛 066004；3. 先进锻压成型技术与科学教育部重点实验室(燕山大学)，河北秦皇岛 066004)

引言

仿真技术应用之前，传统的产品生产需要反复进行模型性能测试，无法对样机性能进行预测，且研发周期长，投入的工作量巨大，研发成本大。计算机仿真技术的出现改变这一现状。通过计算机技术建立虚拟样机，产品的研发改变可以通过虚拟样机来预测相关性能是否符合要求，大大缩短了研发周期，提高了研发效率，也减少了研发成本[1]。

国内工程机械企业在仿真技术方面的研究仍然处于起步状态，对挖掘机的研发与改善也主要是通过实验进行[2]。随着国内工程机械行业对仿真软件的重视，各大高校、企业纷纷推出自己的计算机仿真技术。北京航空学院研制出FPS通用仿真程序[3]，上海交通大学自主研制开发了针对液压原理图的仿真软件包HY-CAD[4]，浙江大学流体传动及控制研究所与国营厂合作开发了液压系统及元件仿真软件系统DLYSIM[5]。卡特彼勒采用仿真技术，结合刚柔耦合的多体动力学模型实现结构强度、疲劳耐久性优化和工作装置的响应性等研究[6]。

综上所述，国内大多计算机仿真对挖掘机机电液系统进行综合研究非常少。本研究针对某型号挖掘机所采用的川崎K5V160斜盘式轴向柱塞泵展开研究，采用AMESim软件进行仿真研究，其在液压系统仿真方面具有方便、准确等特点[7-8]，最终搭建出与实际结构吻合度较好的仿真模型，为搭建出高精度的挖掘机整机仿真模型奠定基础。

1 液压泵特性分析

1.1 结构分析

本研究所采用的液压泵是川崎的K5V160斜盘式轴向柱塞泵如图1所示，液压泵实现的功能为：发动机扭矩传递到轴1，驱动缸体5转动，同时9个柱塞4沿着配流盘6表面滑动。柱塞4在缸体5内往复运动，交替地吸入低压油和释放高压油。通过改变斜盘倾角改变排量。液压泵的结构：缸体5被花键8支撑到轴1上；轴1被前、后轴承9所支撑；柱塞4的顶部被制成凸的球形，与滑靴3一侧的凹槽配合，组成了球面轴承；当滑靴3做圆周运动时，它始终压靠在斜盘的表面A上；柱塞4在缸体5各缸腔内部以轴向进行相对的运动；缸体5密封住至配油盘6的液压油，并进行相对的转动；缸体5的各缸腔内部的油液通过配流盘6被吸入和排出；活塞7在调节器的控制下进行直线往复运动，经由传动销被传递至斜盘2带动斜盘滑动，改变斜盘倾角，进而改变液压泵的排量[9-11]。

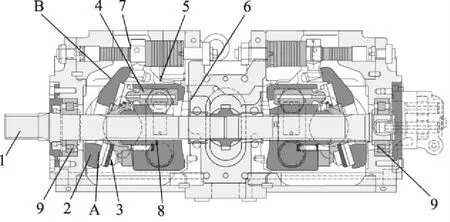
1.前轴 2.斜盘 3.滑靴 4.柱塞 5.缸体 6.配流盘 7.活塞 8.花键 9.前、后轴承图1 液压泵结构示意图

1.2 工作原理分析

本研究采用的液压泵为电控正流量液压泵，该泵具有正流量控制功能、总功率控制功能。如图2所示为液压泵的液压原理图，主要分为三大部分：双联主泵、先导泵、调节器。主泵和先导齿轮泵以串联方式由发动机驱动，每个主泵都有1个单独的调节器调节2个主泵排量。图中，p1、p2为双联主泵中泵1、泵2的出口压力，pz1、pz2为经过电磁比例减压阀的二次压力，pf1、pf2为紧急用时的动力切换指令压力，pi1、pi2为正流量控制压力，i1、i2为控制器输出电流，pSV1、pSV2为先导控制压力。双联主泵在结构上是对称的，后文将对单个泵的排量、功率调节原理和特性进行详细分析[12]。

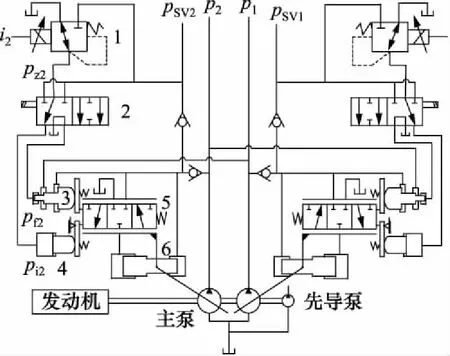
1.电磁比例减压阀 2.电液转换阀 3.变功率调节器 4.正流量调节器 5.伺服换向阀 6.伺服活塞图2 液压泵原理

1.3 正流量控制特性分析

(1) 当指令电流值i增大时，如图3所示，电磁比例减压阀的2次压力上升，于是先导柱塞643朝A的方向移动，直到pz与先导弹簧646的弹力相平衡的位置才停止下来。先导柱塞的移动借助销875被传递给拨杆613，并以B为支点按箭头方向转动。拨杆613的转动又借助F处的销轴传递给反馈杆611，并以C为支点与B作相同箭头方向转动。伴随此，与反馈杆连接在一起的阀芯652朝D方向移动。阀芯朝D方向移动时，使伺服活塞的大直径室与油箱接通，因此伺服活塞的大直径室的压力被卸掉，于是通过小直径室的输出压力p2将伺服活塞532朝E的方向移动，因而使流量增加。因反馈杆与伺服活塞及阀芯连接在一起，所以如伺服活塞朝E的方向移动时，反馈杆便以F支点转动，这样便使阀芯移至原来的位置。通过此移动，滑阀与阀体之间的开口被慢慢关闭，直到在完全关闭的位置伺服活塞才停止不动。

图3 正流量控制流量增加动作

(2) 当指令电流值i减小时，如图4所示，电磁比例减压阀的2次压力下降，于是先导柱塞643被朝G的方向移动，直到pz与先导弹簧646的弹力相平衡的位置才停止下来。先导柱塞的移动借助L处的销轴被传递到反馈杆611并以I为支点与H做相同箭头方向的转动。伴随此，与反馈杆连接在一起阀芯652朝J的方向移动。阀芯朝J的方向移动时，输出压力p2经由阀芯被导入至伺服活塞大直径室。

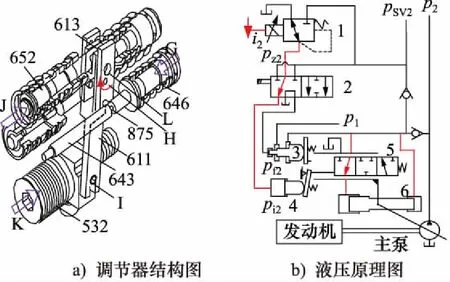
图4 正流量控制流量减小动作

另一方面，伺服活塞小直径室被导入输出压力p2，由此通过面积差使伺服活塞朝K的方向移动，从而使倾角减小，因而使流量也减少了。而反馈杆与伺服活塞及阀芯是连接在一起的，因此伺服活塞朝K的方向移动，此时反馈杆则以L为支点转动，这样便使阀芯移至原来的位置。通过此移动，阀芯与阀体之间的开口被关闭，直到在完全关闭的位置伺服活塞才停止不动。

1.4 总功率控制特性分析

1) 恒功率控制过负载防止动作

当自己方泵输出压力p2上升时，如图5所示，因输出压力p2作用到补偿柱塞621的阶梯部，所以补偿杆623朝M的方向移动，一直移动到输出压力p2与外弹簧625、内弹簧626的弹力相平衡的位置才停止移动。补偿杆的移动借助销875传递给拨杆612并以N为支点按箭头方向回转。接着，拨杆612的移动借助销轴传递到反馈杆611并以O为支点与N作相反箭头方向的转动。伴随此与反馈杆连接在一起的阀芯652朝P的方向移动。阀芯如朝P的方向移动的话，输出压力p2经由阀芯被导入到伺服活塞大直径室。而伺服活塞小直径室被导入输出压力p2，由止通过面积差伺服活塞朝Q的方向移动，从而使倾角减小，因而使流量也减少了。而反馈杆与伺服活塞及阀芯是连接在一起的，因此伺服活塞朝Q的方向移动，此时反馈杆则以R为支点转动，这样便使阀芯移至原来的位置。通过此移动、阀芯与阀体之间的开口被慢慢关闭，直到在完全关闭的位置伺服活塞才停止不动。

图5 恒功率控制过负载防止动作

2) 恒功率控制流量恢复动作

当自己方泵输出压力p2下降时，如图6所示，由外弹簧625和内弹簧626的弹力使补偿杆623朝S的方向移动，一直移动到外弹簧和内弹簧的弹力与输出压力p2相平衡的位置。补偿杆623的移动借助销875传递给拨杆612并以T为支点按箭头方向转动。接着，拨杆612的移动借助J处的销轴传递到反馈杆611并以U为支点与V作相反箭头方向的转动。伴随此、与反馈杆连接在一起的阀芯652朝V的方向移动。阀芯如朝V的方向移动的话，使伺服活塞的大直径室与油箱接通，因此伺服活塞的大直径室的压力被泄掉，于是通过小直径室的输出压力p2使伺服活塞532朝W的方向移动，因而使流量增加。因反馈杆与伺服活塞及阀芯连接在一起，所以如伺服活塞朝W的方向移动的话，反馈杆便以X支点转动，这样便使阀芯移至原来的位置。通过此移动、阀芯与阀体之间的开口被慢慢关闭，直到在完全关闭的位置伺服柱塞才停止不动。

图6 恒功率控制流量恢复动作

3) 总功率控制

当主泵处于稳定工作状态时，伺服换向阀5处于中位，伺服活塞6封闭不动，小腔与泵出口连通为高压状态，由于大腔封闭使得伺服活塞6处于平衡状态。当负载增大，如图7所示，泵出口压力升高，恒功率调节器3左侧液压力增大。当左侧液压力大于右侧弹簧力时，恒功率调节器3向右移动，伺服换向阀5向右移动，伺服活塞6大腔与主泵连通，在大小腔面积差的作用下，伺服活塞6向右移动，主泵排量减小。

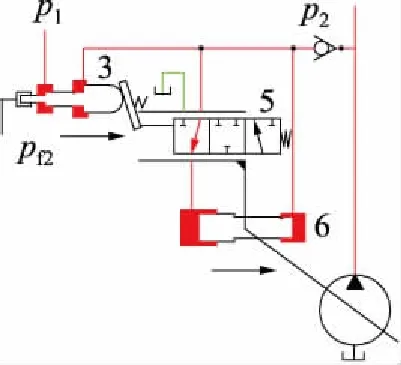
图7 总功率控制

图8 恒功率变化

如图8所示，通过动力切换压力pf可任意控制泵的设定功率。当增大动力切换压力pf时，与功率控制的过载防止动作中说明的一样，可使泵的倾角减小从而减小功率设定值。反之，减小动力切换压力pf时可增大功率设定值。

1.5 泵压力-流量模型

如图9所示为电控正流量泵压力-流量曲线，该曲线是在主泵转速为2000 r/min下的压力-流量曲线，曲线中各符号含义说明如下：

(1) 细实线(a)为调节器pf压力为0时的曲线即泵最大流量曲线；

(2) 细实线(b)为调节器pf压力为3.9 MPa时的曲线；

(3) 粗实线(1)为主泵功率为182 kW的恒功率p-Q曲线；

(4) 粗实线(2)为主泵功率为155 kW的恒功率p-Q曲线；

(5) 双点画线(c)为主泵电磁比例减压阀电流和输出量曲线，该曲线即为正流量控制曲线；

(6) 细实线(d)为泵的最小流量曲线。

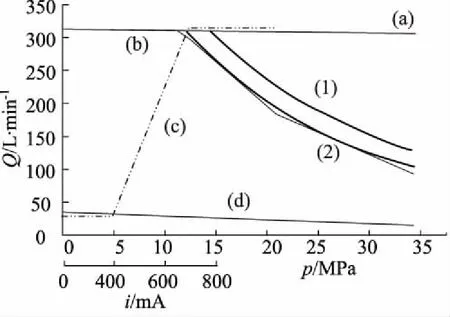
图9 电控正流量泵压力-流量曲线

如图9所示恒功率曲线的横坐标为变量泵的出口压力，纵坐标为变量泵输出流量。由于恒功率控制由两端弹簧实现，因此压力-流量曲线为两段直线以近似恒功率。比例阀电流增大，恒功率曲线上移，功率值增大。正流量控制曲线的横坐标为泵的正流量控制电流，在正流量控制起作用的区段，流量随电流的增大而增大。

(1) 正流量控制模型：

(1)

(2) 恒功率控制模型：

调节器pf压力为0时：

Qp=-0.4956p+318(0≤p≤34.3)

(2)

调节器pf压力为3.9 MPa时：

主泵功率为182 kW时：

(4)

主泵功率为155 kW时：

(5)

2 数学建模

变量泵接收来自于控制器输出的电流值，经电磁比例减压阀转换为压力信号驱动变量泵调节器的运动，从而起到调节变量泵排量的目的。想要获得输入电流-主泵流量关系，需要确定电磁比例减压阀输入电流-二次压力关系以及二次压力-主泵输出流量关系，下列通过数学模型表达二者之间对应关系。

1) 电磁减压阀输入电流i-输出压力pi关系：

(6)

2) 正流量控制活塞方程

如图10所示电磁比例减压阀减压后压力推动正流量活塞运动。正流量控制活塞动力学方程：

(7)

式中，Ac—— 二次压力作用面积，m2

Fz—— 连杆对正流量活塞作用力，N

mc—— 正流量控制活塞组件质量,kg

Bv—— 控制活塞黏阻系数，N/(m·s-1)

kc—— 控制活塞弹簧系数，N/m

xc—— 正流量活塞位移，m

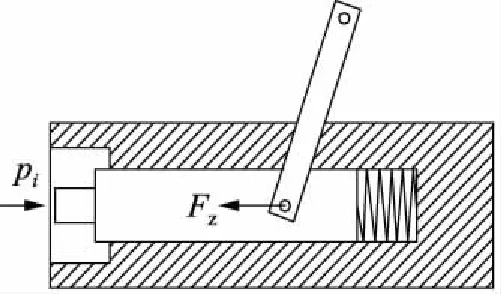
图10 正流量活塞杆示意图

3) 恒功率控制活塞方程

如图11所示压力油经电磁比例减压阀减压后经过电液转换阀推动恒功率活塞运动。恒功率控制活塞动力学方程：

(8)

式中，mp—— 恒功率控制活塞组件质量，kg

xp—— 恒功率活塞位移，m

Bp—— 恒功率控制活塞黏阻系数，N/(m·s-1)

kp—— 恒功率控制活塞弹簧系数，N/m

F1—— 连杆对恒功率活塞作用力，N

A1—— 泵1压力作用腔面积，m2

A2—— 泵2压力作用腔面积，m2

Af—— 动力切换压力作用腔面积，m2

图11 恒功率活塞杆示意图

4) 调节器连杆和反馈杆

正流量活塞的运动带动变量机构连杆绕O1固定销钉转动，连杆的转动通过销钉带动反馈杆绕O2销钉转动，反馈杆通过销钉与伺服阀相连接，带动伺服阀移动，正流量活塞位移与反馈杆位移之间关系如下所示：

xcl1=xsl2

(9)

式中,xs—— 反馈杆和连杆销钉水平距离，m

l1—— 连杆上销钉到固定销钉O1距离，m

l2—— 正流量活塞销钉到固定销钉O1距离，m

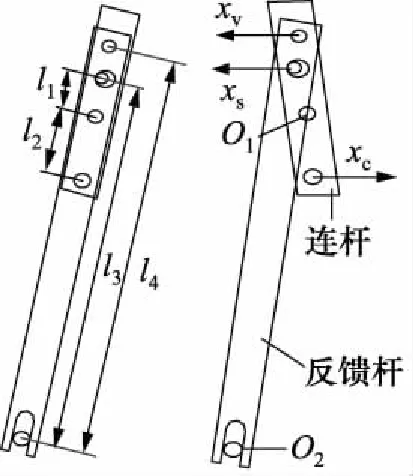
图12 连杆和反馈杆位置、受力示意图

由动力学原理，得到反馈杆位移与伺服阀位移之间关系如下所示：

xsl4=xvl3

(10)

式中,xv—— 伺服阀阀芯位移，m

l3—— 连杆销钉到固定销钉O2距离，m

l4—— 反馈杆与伺服活塞相接的销钉到反馈杆与固定销钉O2距离，m

伺服阀位移与正流量活塞位移之间比例kvc方程为：

(11)

根据调节器运动原理，同理可推导出伺服阀阀芯位移与伺服活塞位移之间比例kvd方程：

(12)

正流量控制活塞位移、伺服活塞位移与伺服阀阀芯位移之间的比例关系：

xv=kvcxc-kvdxd

(13)

式中,kvc—— 伺服阀阀芯位移与正流量活塞位移比例

kvd—— 伺服阀阀芯位移与伺服活塞位移比例

xd—— 伺服活塞位移，m

5) 伺服阀

在变量泵工作过程中变量泵输出压力p随着负载的变化而变化，但是其变化对控制机构的影响并不大，因此将其作为定值处理，伺服阀阀口线性化流量方程：

q1=kqxv-kp1(p-pd)

(14)

式中,q1—— 伺服阀阀口流量，L/min

kq—— 伺服阀阀口流量增益，L/m

kp1—— 伺服阀阀口流量-压力系数，L/MPa

pd—— 伺服活塞大腔压力，bar

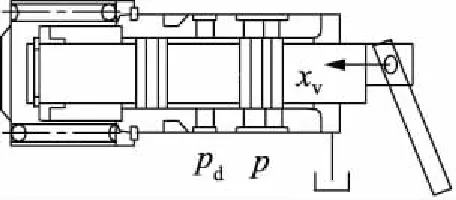
图13 伺服阀示意图

6) 伺服活塞

伺服活塞受力方程：

(15)

式中,Ax—— 伺服活塞小径腔,m2

Ad—— 伺服活塞大径腔，m2

md—— 伺服活塞质量，kg

Bd—— 伺服活塞黏性阻尼系数，N/(m·s-1)

Fsp—— 泵斜盘对伺服活塞的作用力，N

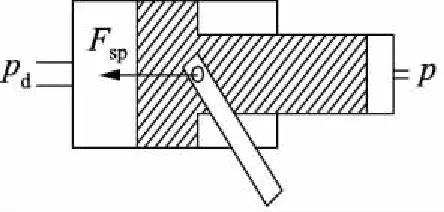
图14 伺服活塞受力示意图

由流量连续性方程可得：

q1=Adxd

(16)

7) 泵斜盘

由几何关系可知，柱塞位移与斜盘倾角，满足如下关系，如图15所示为变量泵斜盘工作原理示意图。

图15 变量泵斜盘工作原理

柱塞由B点转动到任意点的过程中，柱塞沿轴向的位移xe为：

(17)

式中,d1—— 柱塞分布圆直径，mm

β—— 斜盘倾角，(°)

θ—— 旋转角度，(°)

变量泵排量D：

(18)

式中,d—— 柱塞直径，m

z—— 柱塞数量

变量泵流量q：

q=ωD

(19)

式中,ω—— 发动机转速，r/min

3 AMESim仿真模型建立

根据K5V泵变量机构特点以及数学模型，建立变量泵AMESim仿真模型如图16所示，建模难点在于如何确定电磁比例减压阀-正流量调节器(恒功率调节器)-伺服阀-伺服活塞-变量泵排量之间的传递关系。这些传递关系在仿真模型中依靠各机构参数来实现，然而参数获取往往受到结构等一些限制，难度较大。

1.电磁减压阀 2.变功率调节器 3.正流量调节器 4.伺服换向阀 5.伺服活塞 6.阀芯位移-斜盘角度函数 7.液压泵 8.换向阀 9.液压缸 10.先导图16 K5V变量泵仿真模型

主泵参数来源主要依靠实际测量、查找样本、根据所搭建数学模型进行参数完善等方法获得。表1所示为主泵变量机构仿真模型参数，将参数分别输入仿真模型相应位置。其中kvc比例关系由正流量活塞连杆和反馈杆共同决定，即伺服阀位移与正流量活塞位移之间比例关系，同理kvd由连接恒功率活塞和伺服阀之间连杆和反馈杆共同决定，即伺服阀位移与变功率控制活塞位移之间比例关系。

表1 K5V泵变量机构仿真模型参数表

对比如图2变量泵实际原理与图16中K5V泵仿真模型可以看出，仿真模型结构与真实K5V变量泵基本相似。手柄先导压力信号10通过控制器处理转变为电流信号，通过电磁减压阀1转变为二次压力，推动正流量调节器3(变功率调节器2)运动，经过运算其位移值，控制伺服换向阀4阀芯运动，从而改变伺服活塞5的移动方向，再将伺服活塞5的位移反馈给伺服换向阀4阀套，使伺服换向阀4回到中位，控制伺服活塞5运动到设定位移，从而改变泵7的排量到设定值。液压泵7输出流量经过换向阀8进入液压缸9。

验证液压泵正流量控制方式下，先导压力信号和主泵输出流量的关系，此模式下不考虑恒功率控制特性，主泵排量只与先导输入信号有关，与工况无关。具体步骤如下：

在图16仿真模型下设置主泵出口压力为5 MPa，仿真时间设定为10 s，先导电流信号从0～750 mA,发动机转速为恒定值2000 r/min。仿真结果如图17所示，K5V变量泵单泵最大排量为160 mL/r，由于仿真模型忽略主泵的泄漏等因素，因此仿真数值为320 L/min比实际最大流量313 L/min稍大。

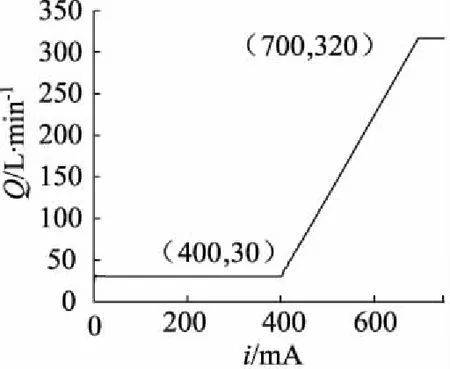
图17 电流-流量曲线

验证液压泵恒功率控制方式下，泵出口压力信号和泵输出流量的关系，此模式下主泵输入电流为最大值，即不考虑正流量控制特性，主泵排量只与负载压力有关，与先导压力无关。具体步骤如下：

设定变量泵转速为2000 r/min，主泵排量为160 mL/r，pf压力为3.9 MPa，主泵压力从0上升到34.3 MPa。当系统压力到达设定值时，K5V正流量泵进入恒功率控制方式，通过电磁减压阀使二次压力达到设定值，切换电液转换阀使压力油进入恒功率调节器，主泵流量开始发生变化。仿真结果如图18所示，当压力小于12 MPa时主泵流量处于最大值；当压力到达12 MPa时主泵流量随着主泵出口压力增加而减少；当压力为22 MPa时，主泵流量随压力变斜率发生改变，因为K5V恒功率变量机构在系统压力为22 MPa 之前恒功率控制腔只有一根弹簧工作，当主泵压力到达22 MPa时，恒功率控制部分两根弹簧工作。

对比图17与图9中正流量控制曲线即双点划线曲线，二者之间高度吻合。由于正流量控制信号实际输入范围为0～750 mA，与仿真模型输入完全相符，即仿真模型覆盖所有正流量控制范围，因此该泵正流量控制特性建模准确。

对比图18与图9中曲线(b)，二者之间高度吻合。由于液压泵不同功率设定值对应的pf值不同，根据式(8)可以确定不同功率设定值对应的pf值，在仿真模型中将pf值修改为对应值即可，因此该泵恒功率控制特性建模准确。

图18 压力-流量曲线

4 实验研究

4.1 实验原理与测点布置

上文针对仿真模型进行了正流量控制特性和恒功率控制特性校核，均属于静态特性校核，为进一步验证所搭建仿真模型的动态特性，下文将进行实验研究。由于挖掘机的挖掘作业备受用户与厂商关注，且占据挖掘机工作总时长比例较多，因此选取动臂提升、斗杆挖掘以及铲斗挖掘三个典型动作为例进行实验研究。实验样机、测试仪器安装位置如图19所示。

图19 实验测试安装图

以铲斗挖掘动作为例进行实验说明：首先进行铲斗工作装置姿态的标定，铲斗挖掘工作装置初始姿态为动臂上表面处于水平位置，斗杆上表面垂直于地平面，铲斗挖掘起始铲斗姿态为铲斗活塞全缩，挖掘过程中铲斗活塞杆逐渐伸出，当铲斗活塞杆伸出到最终端位置时，铲斗挖掘机动作结束，如图20所示。同理进行动臂提升、斗杆挖掘动作姿态标定，如图21所示。

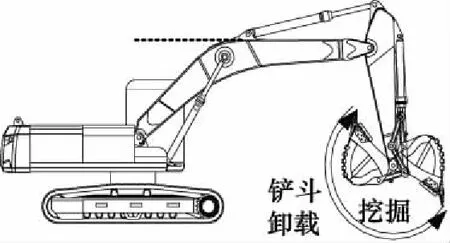
图20 铲斗动作姿态标定示意图

图21 挖掘机姿态标定示意图

以铲斗挖掘为例：工作装置姿态标定结束后，动臂、斗杆和铲斗油缸位置保持不动，具体实验步骤如下：

(1) 挖掘机初始姿态为上述所示，关闭驾驶室空调，进行铲斗挖掘单动作操作；

(2) 调定发动机转速，设定发动机模式为十挡；

(3) 通过操作手柄使先导压力逐渐增加，使铲斗挖掘直至溢流；

(4) 铲斗复位后重复实验动作，采集所需流量、压力和位移数据曲线如图22所示；

(5) 同理进行斗杆挖掘、动臂提升实验研究，实验数据如图23、图24所示。

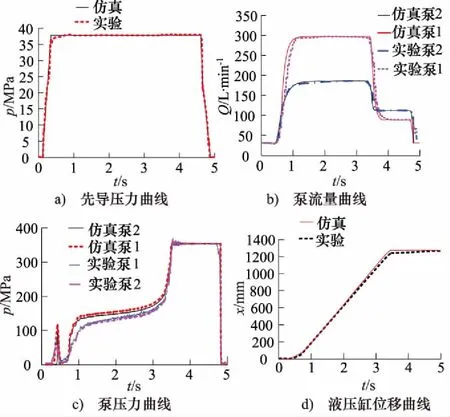
图22 铲斗挖掘动作仿真与实验对比

4.2 实验与仿真对比

将实验采集的先导压力、负载数据，导入图16所示的仿真模型中进行铲斗挖掘、斗杆挖掘以及动臂提升仿真，所得曲线如图22～图24所示。

铲斗挖掘动作如图22所示，先导压力在0.34 s时达到最大值3.8 MPa，仿真泵2流量从30 L/min上升到187 L/min，仿真泵1流量从30 L/min上升到300 L/min，与实验数据变化趋势一致。在3.2 s时泵1、泵2压力迅速上升到35 MPa，液压泵在压力上升过程中进入恒功率状态，泵2流量减少至112 L/min，泵1流量减少至88 L/min，与实验数据相同。整个挖掘过程仿真泵1、泵2压力变化趋势与实验数据一致，均在0.34 s 处出现一个压力高峰，在3.2 s处压力迅速上升至35 MPa。由于仿真模型中输入负载为实验采集的液压缸大小腔压力经理论计算所得与实际负载存在一定误差，所以当铲斗液压缸匀速运动时，泵1、泵2仿真压力比实际压力都要大2 MPa左右。

图23 斗杆挖掘动作仿真与实验对比

图24 动臂提升动作仿真与实验对比

泵的流量响应特性精度YQ：

(20)

泵的压力响应特性精度Yp：

(21)

选取图22仿真曲线与实验曲线中的数据点，采用式(20)、式(21)进行计算，铲斗挖掘动作泵1、泵2的流量响应特性精度分别为92%，95%，压力响应特性精度达到84%，92%。

斗杆挖掘机动作如图23所示，先导压力在0.64～1.05 s达到最大值3.8 MPa，仿真泵2、泵1流量迅速上升到285 L/min，与实验中泵1、泵2流量最大值相等，但仿真流量比实验流量快0.1 s到达最大值。在3.94 s 时泵1、泵2压力迅速开始上升到35 MPa，液压泵在压力上升过程中进入恒功率状态，泵2、泵1流量减少至100 L/min与实验数据吻合。整个挖掘过程仿真泵1、泵2压力变化趋势与实验所测高度吻合，均在0.83 s处出现一个压力高峰，在4.1 s处压力迅速上升至35 MPa。同理根据图23计算泵1、泵2的流量响应特性精度均为95%，压力响应特性精度为89%，90%。

如图24所示先导压力0.64～1.05 s达到最大值3.8 MPa，仿真泵1、泵2流量迅速上升到262 L/min，与实验中泵1、泵2流量最大值一致，但仿真流量比实验流量快0.5 s到达最大值。在3.94 s时泵1、泵2压力迅速开始上升到35 MPa，液压泵在压力上升过程中进入恒功率状态，泵1、泵2流量减少至100 L/min与实验数据吻合。整个挖掘过程仿真泵1、泵2压力变化趋势与实验所测高度吻合，均在0.64 s处出现一个压力高峰，在3.77 s处压力迅速上升至35 MPa。同理根据图24计算泵1、泵2的流量响应特性精度分别为87%，88%，压力响应特性精度均为95%。

综上所述，将动臂、斗杆、铲斗3组数据的流量响应精度、压力响应精度求平均值分别为91.6%，91%，因此泵1、泵2的仿真模型在阶跃信号下的平均流量响应精度和平均压力响应精度均能达到90%，即变量泵动态特性精度达到90%。