谱估计理论在弹道数据参数化建模中的应用

张 召，荆武兴，李君龙，高长生

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 中国航天科工集团有限公司第二研究院，北京 100854)

0 引 言

凭借高速度和高机动性能，高超声速飞行器具备极强的突防能力，对现代防御体系构成了巨大威胁。为对其进行有效的跟踪、预报和拦截，需要对其弹道特性进行深入研究，了解其运动规律并进行参数化建模。

目前针对弹道特性的研究，大都基于飞行器的动力学模型，采用基于标称弹道的线性化[1-2]、分岔理论[3-4]和多尺度理论[5-6]等方法，研究制导参数对弹道数据的影响规律。然而，对于防御方来说，进攻方飞行器的制导规律和动力学模型是不可观测的，而且在线识别的技术难度较大[7]。因此，本文将飞行过程视作黑箱模型，针对可观测的弹道数据开展研究，分析其变化规律并给出参数化描述。相较于传统研究方法，本文方法着重于挖掘弹道数据自身的内在规律，可以为不同飞行器提供统一的弹道描述方式，而且易于利用跟踪数据进行在线建模，为实现弹道层面的匹配、识别和预报奠定基础[8-9]。

针对数据内在规律的挖掘，时间序列分析以及信号处理等领域都有丰富的研究成果。信号处理领域的谱估计理论，可以在输入未知的情况下，对平稳输出序列进行分析和建模。尤其是功率谱估计，是经常被采用的一种重要方法，反映了信号功率随频率的分布。具体可分为经典谱估计和现代谱估计[10]，其中现代谱估计的参数模型法可以给出信号的参数化描述。以参数模型法描述目标运动已有诸多研究，文献[11-13]使用自回归(Auto-regressive，AR)模型描述人和机器人的运动规律并进行预报；文献[14-16]采用AR模型提取弹道目标的进动特性；文献[17-18]则在模型中引入了输入量，研究竞技体育中目标的轨迹特性。数据平稳是应用谱估计理论的前提，但是高超声速飞行弹道数据带有明显的趋势，不符合该前提。本文采用线性消势法消除弹道数据的线性趋势，将其转变为平稳信号，进而采用谱估计理论进行分析和建模。

应用参数模型的过程中，最重要的步骤之一就是模型阶数的选择。作为一般规律，如果模型阶数选择太低，将会得到一个高度平滑谱；如果选择得太高，则可能在谱中引入虚假低峰[10]。为此，相关学者提出了不同的选择准则：F-检验、最终预报误差(Final prediction error，FPE)准则、Akaike信息准则(Akaike information criterion，AIC)、贝叶斯信息准则(Bayesian information criterion，BIC)等。然而，一些试验结果表明，模型阶数选择准则不能生成确定的结果[10]。为克服该问题，本文将经典谱估计引入模型阶数的选择过程。以经典谱估计生成的弹道数据谱图为参考，对参数模型阶数进行调整，以完成模型阶数的确定。

本文以高超声速飞行弹道为对象，研究参数化建模方法。以典型弹道数据为基础，使用线性消势法将其转变为平稳信号；综合使用经典谱估计中的Welch直接法和现代谱估计中的AR参数模型法，对弹道数据进行参数化分析和建模。文章最后以弹道地心距为例进行了仿真校验，验证了本文算法所确定模型与动力学模型的一致性。

1 高超声速飞行弹道

进行弹道数据谱估计的基础是充足的数据支持，既可以是先验的弹道数据，也可以是实时的跟踪数据。本节以动力学模型和典型飞行模式为基础，通过数值仿真方法获得典型高超声速飞行器的先验弹道，为后文分析其变化规律并实现参数化建模提供数据支持。高超声速飞行在弹道系下表示为[19]：

(1)

(2)

(3)

(4)

(5)

(6)

典型的飞行模式包括常攻角飞行、常升阻比飞行、最大升阻比飞行、平衡滑翔飞行以及指标最优飞行[20]。其中指标最优包括：射程最优、末速最大、气动加热最少以及突防性能最优等[21-24]。

2 基于Welch算法的弹道数据分析

将弹道数据视作信号，使用信号处理领域的谱估计理论对其进行研究。在实际工作中，往往假定信号是平稳的和各态遍历的[10]。然而，高超声速飞行弹道除了小范围的波动外，具有明显的趋势，直接进行谱估计会导致较大的偏差。本节采用线性消势法提前消除信号的趋势，将其转变为平稳信号，再使用经典谱估计理论生成信号的谱图。

2.1 消除信号趋势

消除信号趋势的主要方法有线性消势和差分消势。考虑到差分消势会引入运动的高阶信息而且高超声速飞行弹道具有波动特性，采用差分消势会导致较高的模型阶数，增大计算量甚至引入虚假低峰。本文采用线性消势法，将数据信号的趋势表述为线性形式：

d(n)=a+bn

(7)

结合生成的弹道数据，以拟合方式确定式(7)系数；然后从原始信号中消除相应的线性部分，即可完成消势。消除趋势后的数据信号可视作平稳的和各态遍历的，可以开展进一步的研究。

2.2 Welch算法

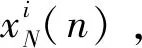
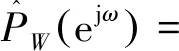
(8)

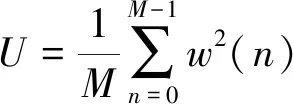
Welch算法很好地改善了周期图法谱估计的方差特性，而且概念清晰、方法简便。本文采用Welch算法对弹道数据进行初步分析，给出大致的功率谱特性，为后文进行更加精确的谱估计和参数化建模提供参考。

3 基于AR模型的弹道数据参数化建模

经典谱估计可以给出大致准确的谱图，但是无法给出数据的参数化描述，不利于开展进一步的研究。现代谱估计的AR参数模型法不仅可以提高功率谱估计的分辨率，而且可以建立数据的参数化模型。然而，仍存在模型阶数选择准则引起的不确定性问题。本节采用AR模型描述弹道数据的内在规律，以改进的协方差法为基础对其进行求解，并结合AIC、AR模型谱图和Welch算法谱图确定具体的模型阶数。

3.1 平稳信号的AR模型

假定所研究信号x(n)是由一个输入信号u(n)激励一个线性系统H(z)的输出，则x(n)和u(n)之间有如下关系：

(9)

式中：若x(n)是确定性的，那么u(n)是一个冲激序列；若x(n)是随机的，那么u(n)是一个白噪声序列。

如果b1,b2,…,bq全为0，则有：

(10)

在Z域上，转移函数为：

(11)

可见，上述模型仅有极点，这种全极点模型即为AR模型。其含义是，模型当前输出由当前输入和过去p个时刻的输出决定。

本文中输入序列是不可观测的，但是如果输出序列表现为平稳随机过程，那么输入序列也被假定为平稳随机过程[10]。因此，假定u(n)是一个白噪声序列，方差为σ2；由随机信号通过线性系统的理论可知，x(n)的功率谱为：

(12)

确定式(12)中的白噪声方差σ2及模型的系数a1,a2,…,ap，即可求出x(n)的功率谱。

3.2 AR模型系数确定

目前提出的有关AR模型系数的求解及AR模型性能的讨论大都是建立在线性预测理论上的，而且这些算法的性能一般要优于自相关法[10]。而且AR模型和线性预测器是等价的，AR模型的白噪声能量σ2等于线性预测器的最小预测误差功率ρmin。不失一般性，令前后预测误差功率之和：

(13)

为最小。上标f表示前向预测，上标b表示后向预测。式(13)中：

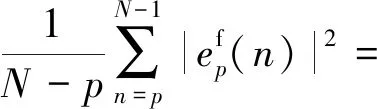
(14)

(15)

在令ρfb为最小时，不是仅令ρfb相对am(m)=km为最小，而是令ρfb相对am(1),am(2),…,am(m)都为最小，m=1,…,p。

由ab(k)=af*(k)，令

(16)

(17)

即

(18)

又令

(19)

写成矩阵形式：

(20)

最小预测误差功率可由式(21)～(22)求出：

(21)

或者

(22)

式(22)即为改进的协方差方法的正则方程，许多学者给出了相应的求解算法[10]。

3.3 AR模型阶数选择

为解决上述问题，本文将经典谱估计引入AR模型阶数的选择过程：首先，模型阶数由1逐步增加，计算AIC：

(23)

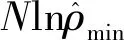
本节所设计的模型阶数选择算法，综合考虑了时域指标和频域指标，分别从时域和频域两个角度分析所建模型的精度。其中，时域指标由改进的协方差方法求解得到，描述了模型误差的统计特性；频域指标由Welch算法的估计结果提供参考，用以评估AR模型谱图的质量。两个指标的综合运用，可以有效改善仅有时域指标造成的不确定性问题，提高建模精度和可靠性。

4 仿真校验

以HTV-2最大升阻比飞行弹道的地心距为例进行仿真分析，初始高度45 km，速度6 km/s，当地速度倾角0°，飞行时长1178 s，采样周期0.1 s，地心距如图1所示。可见地心距呈现波动下降，并且振荡幅值逐步衰减。下面将地心距数据视作信号，分析其功率谱并建立参数化模型，最后对所建立的模型进行验证。

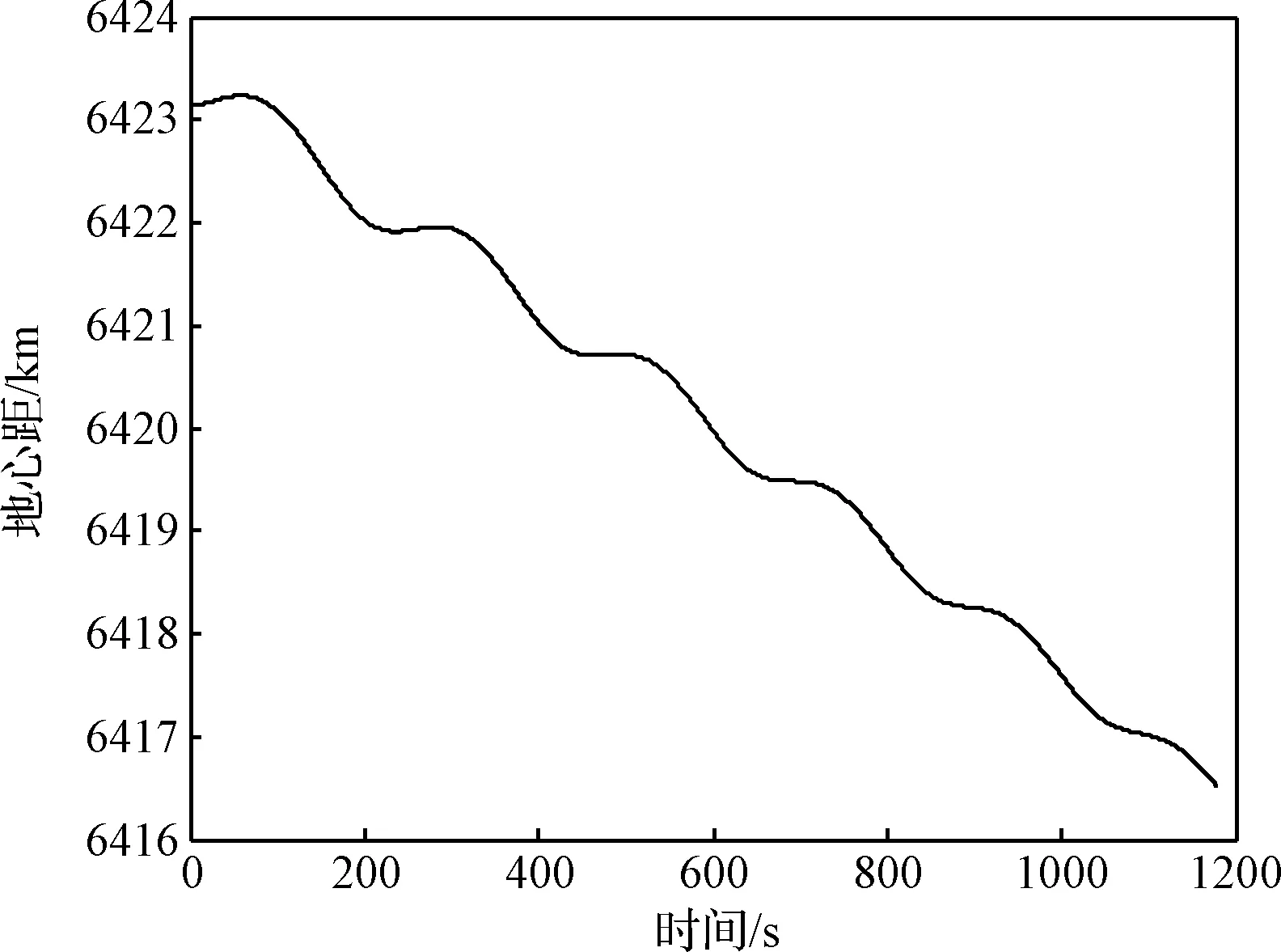
图1 地心距信号时域图Fig.1 Time domain diagram of geocentric distance signal

使用Welch算法分析地心距信号的功率谱，如图2所示。可见在0.02667 rad/s处存在一个转折频率，而且在低频部分存在更大的能量。对照地心距信号时域图可知，地心距为非平稳信号，呈现波动减小趋势：小范围波动即为转折频率所代表的部分，减小趋势即是低频部分。该非平稳信号具有较大的频域跨度，不利于对信号进行精确分析和建模，需要消除信号的趋势，也就是消除其低频部分。

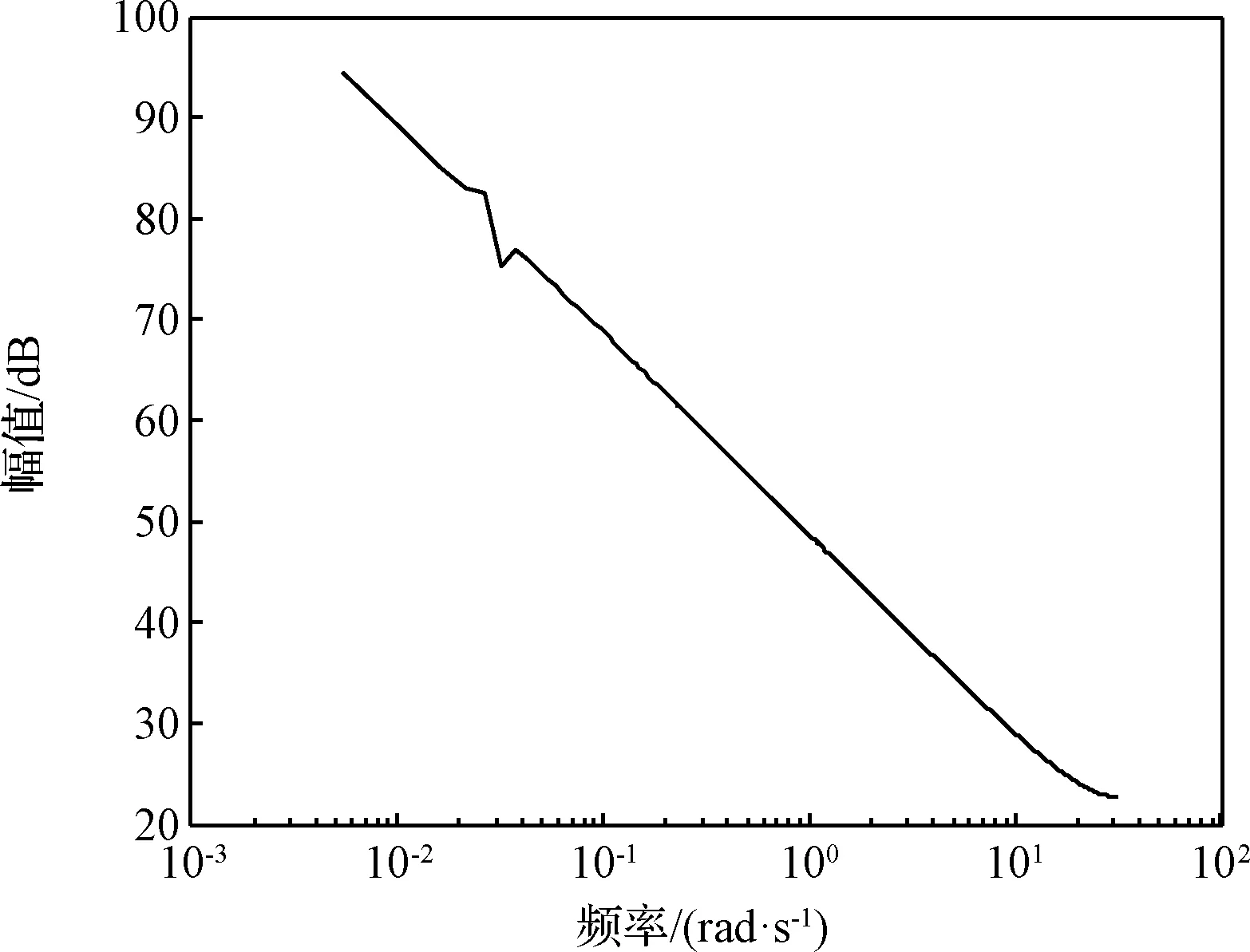
图2 Welch算法确定地心距信号的谱图Fig.2 Spectrum of geocentric distance signal via Welch algorithm

采用线性消势法消除地心距信号的趋势，经拟合确定的趋势表述为(单位：m)：

d(n)=6.4235×106-5.8370n

(24)

消除地心距信号中相应的线性项，得到线性消势地心距信号，如图3所示。可见信号在0值附近振荡，且为衰减振荡，整体仍存在小幅度的非线性趋势。

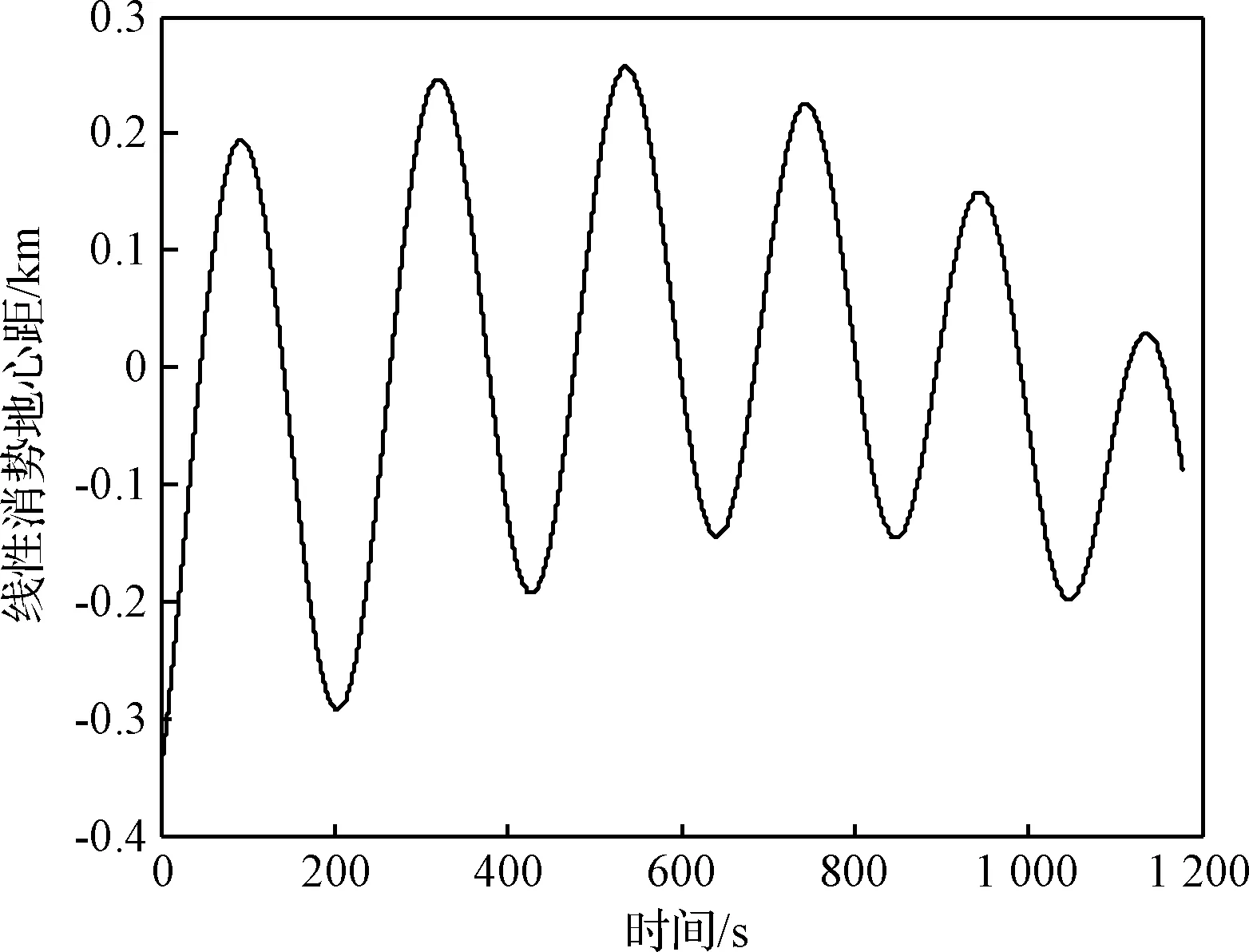
图3 线性消势地心距信号时域图Fig.3 Time domain diagram of linearly detrended geocentric distance signal

使用Welch算法分析线性消势地心距信号的功率谱，如图4所示。可见第一峰值频率为0.032 rad/s、第二峰值频率为0.02667 rad/s，该频段集中了大部分能量，在低频部分存在一个小峰值。对照信号时域图可知，衰减振荡即为第一和第二峰值所代表的部分，整体小幅度非线性趋势即是低频峰值所代表的部分。

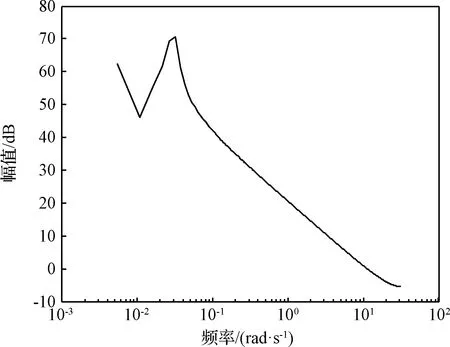
图4 Welch算法确定线性消势地心距信号的谱图Fig.4 Spectrum of linearly detrended geocentric distance signal via Welch algorithm

使用AR模型对线性消势地心距信号进行功率谱估计。首先，模型阶数由1逐步增加并计算AIC，确定AIC最优阶数为3，则阶数选择范围定为2，3，4。下面分别使用这三种AR模型进行功率谱估计，如图5～7所示，可知线性消势地心距信号的峰值频率分别为0.02769 rad/s、0.02894 rad/s、0.01001 rad/s和0.02944 rad/s。

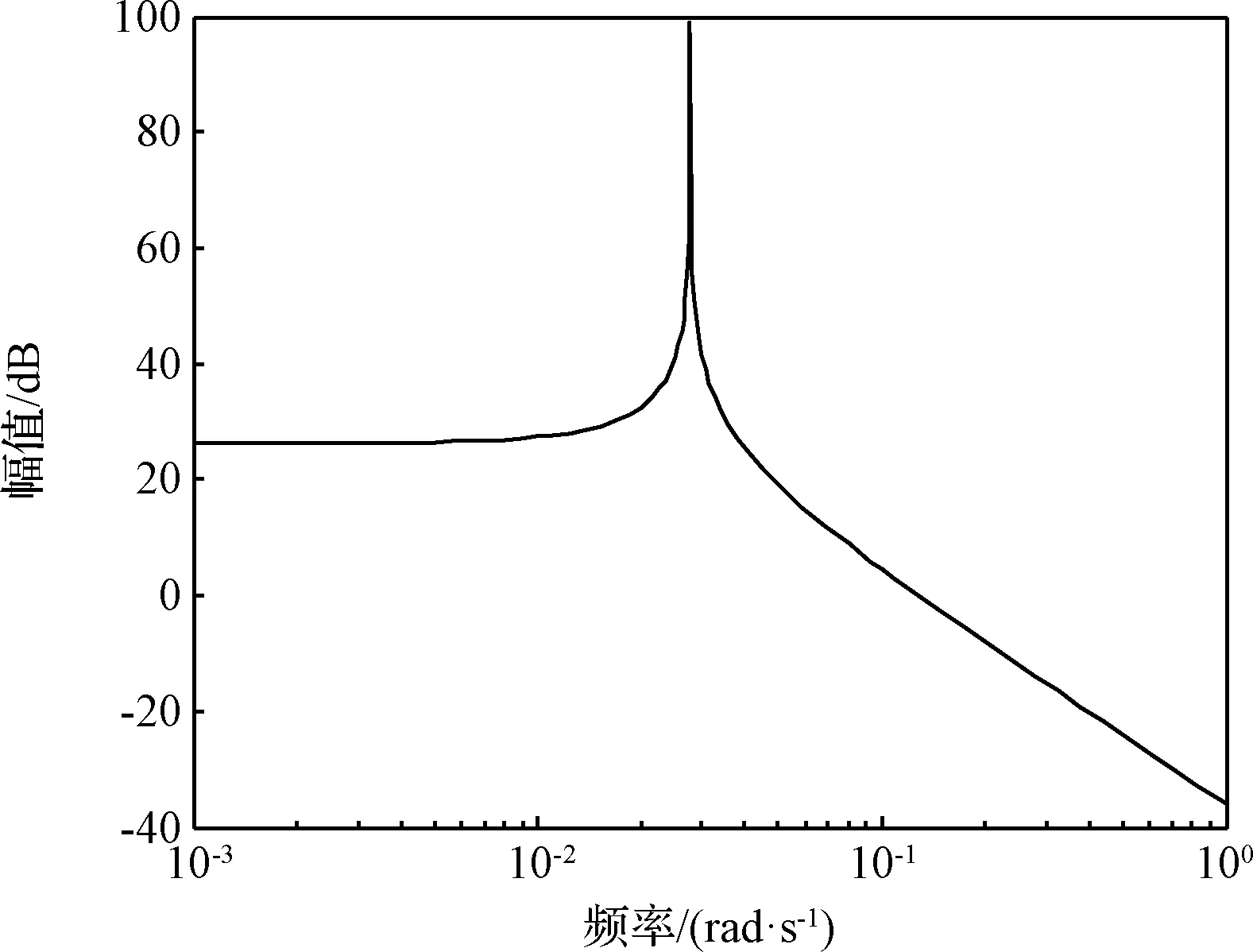
图5 2阶AR模型确定线性消势地心距信号的谱图Fig.5 Spectrum of linearly detrended geocentric distance signal via second-order AR model

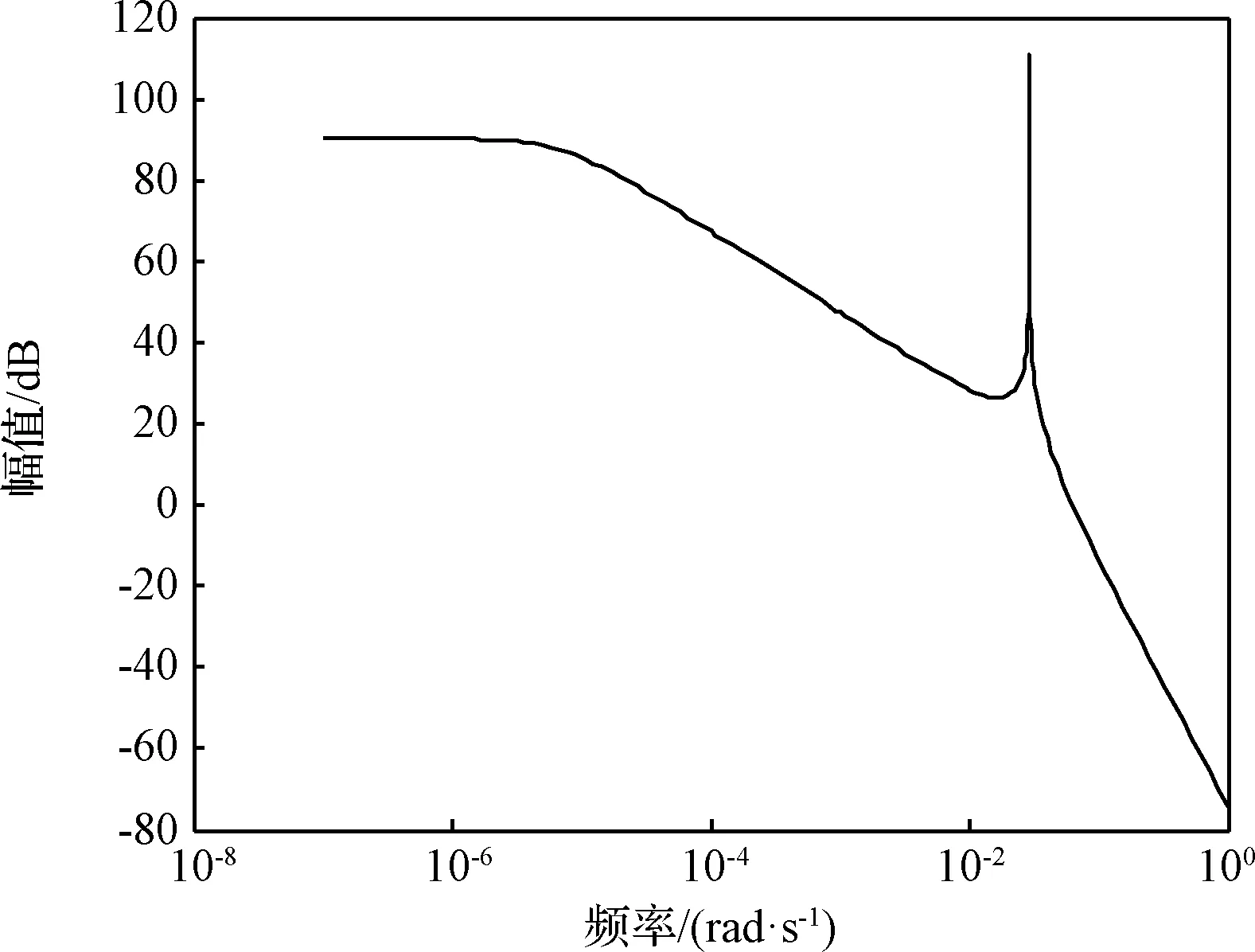
图6 3阶AR模型确定线性消势地心距信号的谱图Fig.6 Spectrum of linearly detrended geocentric distance signal via third-order AR model

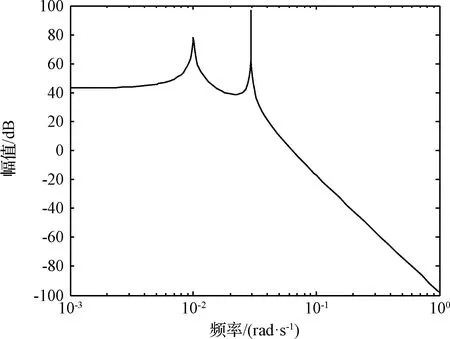
图7 4阶AR模型确定线性消势地心距信号的谱图Fig.7 Spectrum of linearly detrended geocentric distance signal via fourth-order AR model

结合时域图以及Welch算法的谱估计结果可知，线性消势地心距信号的峰值频率在0.02667～0.032 rad/s之间，而且在低频部分存在一个小峰值。2阶和3阶AR模型均识别出该范围内的一个峰值，4阶AR模型则识别出该范围内一个峰值和范围外一个低频峰值。3阶AR模型虽然是AIC最优的，但其低频部分仍存在较大的能量，因此其对信号的描述是不准确的，其输出存在低频漂移。2阶和4阶模型识别出窄尖峰谱线，对信号的刻画较为准确。识别得到的线性消势地心距AR模型分别为(单位：m)：

A(z)x(n)=u(n)

(25)

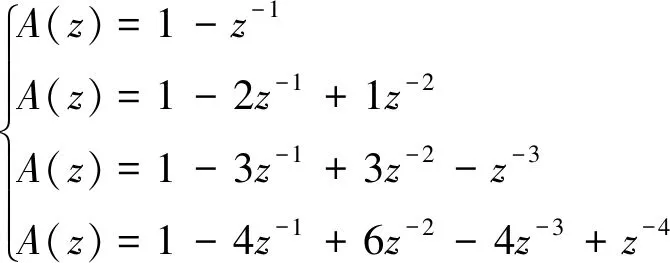
(26)

则完备的地心距模型为经线性补偿的AR模型(Linearly compensated AR model，LAR)：

r(n)=x(n)+d(n)=x(n)+

6.4235×106-5.8370n

(27)

下面对上述模型进行校验，基本思想为：将动力学模型作为参考，考察在相同初始条件下LAR模型输出与动力学模型输出的一致性程度；其中LAR模型的输出称为LAR数据，动力学模型的输出称为参考数据。验证指标为：以均值和标准差检验两样本的基本性能参数是否一致；采用秩和检验法校验两样本概率分布的一致性[25]。

首先，由动力学模型生成地心距的真实数据，并在相同初始条件下使用上述LAR模型对地心距进行预报，结果如图8～9所示。可见，1阶模型给出的预报结果是线性的，预报误差随着弹道的振荡而波动；2阶模型、3阶模型和4阶模型预报结果都是波动形式，频率和振幅与动力学模型给出的真实值一致。

然后，考察LAR数据与参考数据的一致性程度，如表1所示。秩和检验中，0假设为两样本概率分布一致，1假设为不一致。可见1阶和3阶模型的均值偏离参考值较大，未通过秩和检验，这是输出的低频漂移造成的；2阶和4阶模型通过了秩和检验，与动力学模型具有较高的一致性，验证了本文方案的有效性。

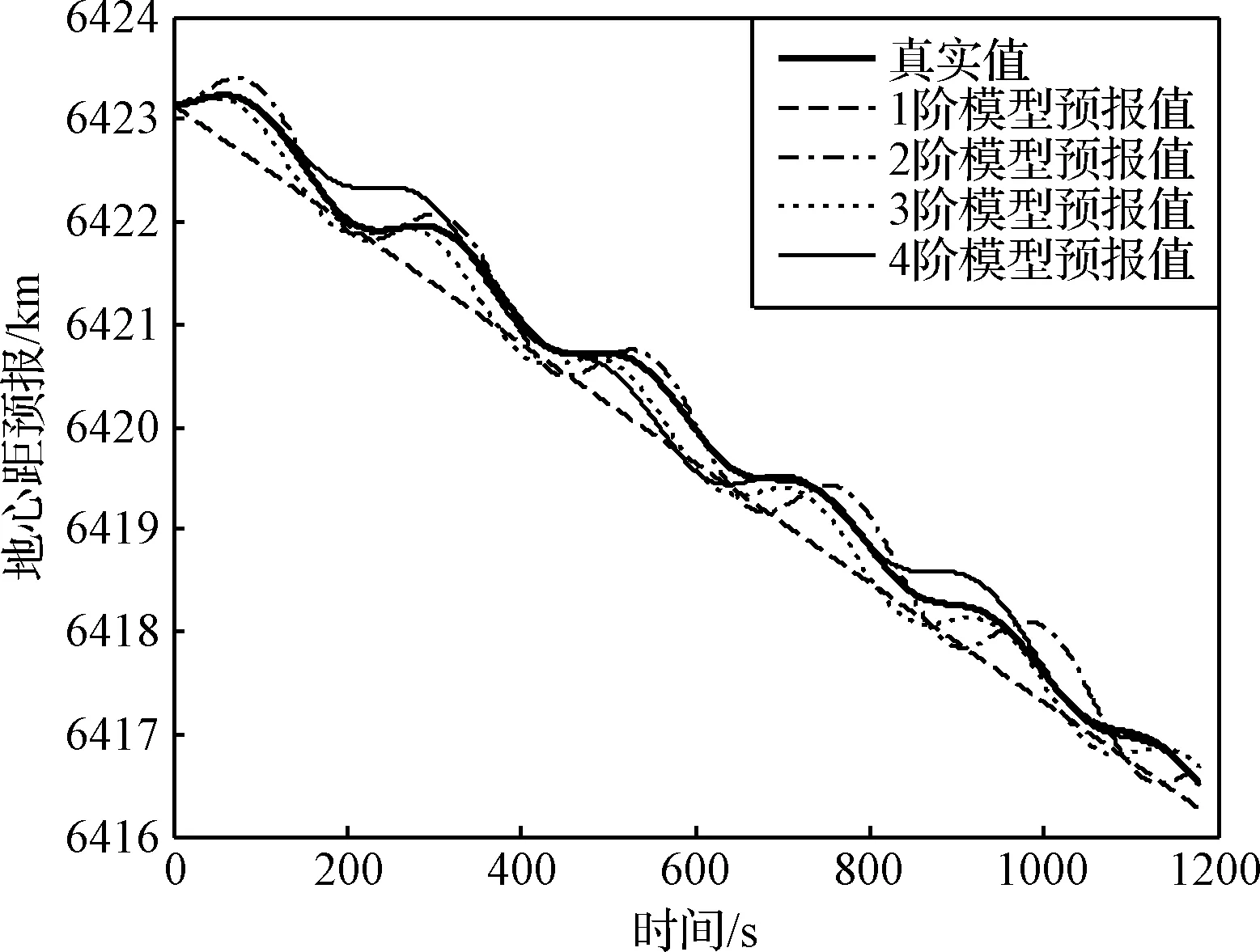
图8 地心距预报结果Fig.8 Prediction results of geocentric distance

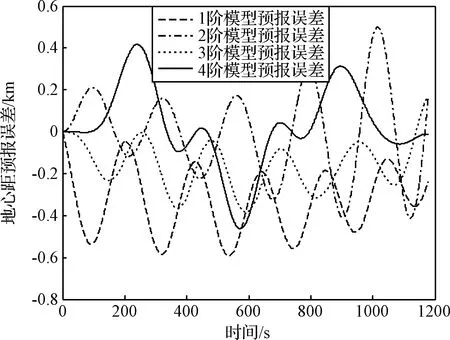
图9 地心距预报误差Fig.9 Prediction error of geocentric distance

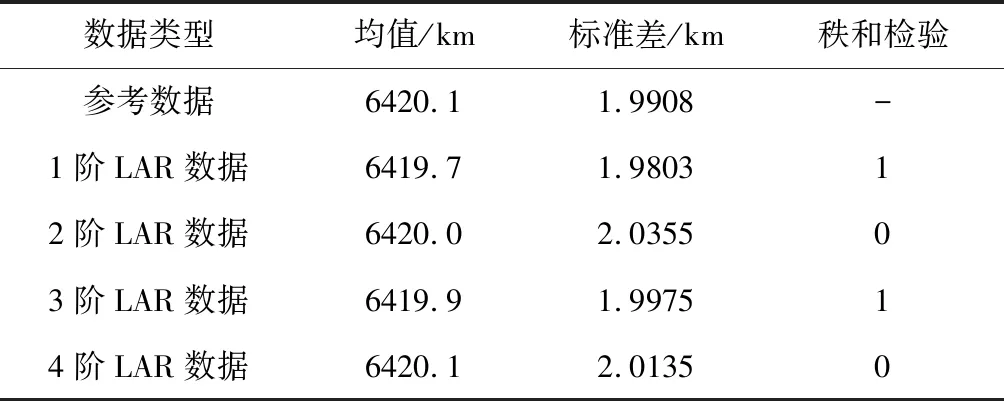
表1 模型校验结果Table 1 Model validation results

5 结 论

本文综合运用信号处理领域的经典和现代谱估计理论，对弹道数据进行分析和建模。由Welch算法确定大致的谱图，然后由AR模型进行精确的功率谱估计，并给出弹道数据的参数化模型。针对弹道数据非平稳特性，本文采用线性消势法对信号进行消除趋势操作；针对模型阶数选择准则无法给出确定结果的问题，本文提出综合经典和现代谱估计的谱图，确定AR模型的阶数。仿真结果表明，针对以线性趋势为主要趋势并带有小幅波动的高超声速跳跃弹道，以本文方法确定的LAR模型与动力学模型具有较高的一致性。