一类强耦合强不确定性强非线性快时变系统复合控制
2020-01-14宁国栋王松艳
孔 雪,宁国栋,杨 明,王松艳,晁 涛
(1. 哈尔滨工业大学航天学院控制与仿真中心,哈尔滨 150080;2. 复杂系统控制与智能协同技术重点实验室,北京 100074;3. 北京机电工程研究所,北京 100074)
0 引 言
随着飞行器的跨空域、宽马赫数范围飞行,飞行器显现出强耦合强不确定性强非线性快时变特性,对控制提出了非常高的要求,这类强耦合强不确定性强非线性快时变特性系统的控制问题已成为控制界的最具挑战性的课题之一[1-10]。
基于强耦合强不确定控制的考虑,滑模控制是一种切实有效的方法[11]。在滑模控制中,系统状态和系统参数与系统结构无关,仅取决于滑模平面的设计,实现了系统的解耦。滑模控制的最大优点就是系统一旦进入滑模状态,系统状态的转移应不再受系统原有参数变化和外部扰动的影响,对系统参数和外部扰动具有完全的或较强的鲁棒性和不变性。基于强非线性快时变控制的考虑,轨迹线性化控制被提出[12],其本质是首先利用被控对象开环的伪动态逆将轨迹跟踪问题转化为一个非线性时变的跟踪误差调节问题,然后设计闭环的状态反馈控制律使得整个系统获得满意的控制性能。基于智能化的考虑,模糊控制是利用模糊集合理论,把人的模糊控制策略转化为控制算法,适用于权重调度。
综合利用滑模控制、轨迹线性化控制、模糊控制,提出一种适用于强耦合强不确定性强非线性快时变的复合控制方法。
1 一种适用于强耦合强不确定性强非线性快时变的复合控制
1.1 问题描述
对于非线性多输入多输出系统:
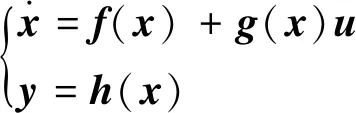
(1)
式中,u∈Rm为输入,f∈Rn,g∈Rn×m和h∈Rm是状态变量x∈Rn的光滑有界函数。假定其受一般形式的摄动和外扰,则:

(2)
式中,Δf∈Rn和Δg∈Rn×m为系统摄动,ζ∈Rn为外扰。基于系统跟踪问题引入以下假设:
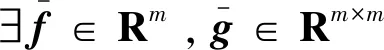
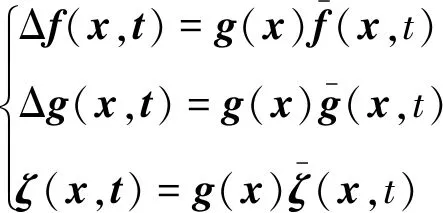
(3)
1.2 基于强耦合强不确定性控制
针对耦合特性具有强不确定性的对象,将子系统间耦合视为干扰,滑模控制(Sliding mode control,SMC)是一种适用的控制方法。为进一步提高强耦合强不确定性的控制能力,采用自适应滑模控制权衡滑模区域大小和滑动模态的响应速度[13],采用滑模状态观测器观测摄动和干扰[11]。但对于滑模控制,存在固有抖振特性,考虑在滑模面附近带内,选用其它控制方法来弥补SMC的不足。
1)自适应滑模控制
定义1.以PD型滑模面为例,常规PD型滑模面选取如式(4)。式中,e为状态偏差。定义滑模面斜率为c=c1/c2。
(4)

结合滑模控制的基本条件,以二阶系统为例,分析c选取原则,结论如式(5)所示,式中,λ1和λ2为系统特征根。
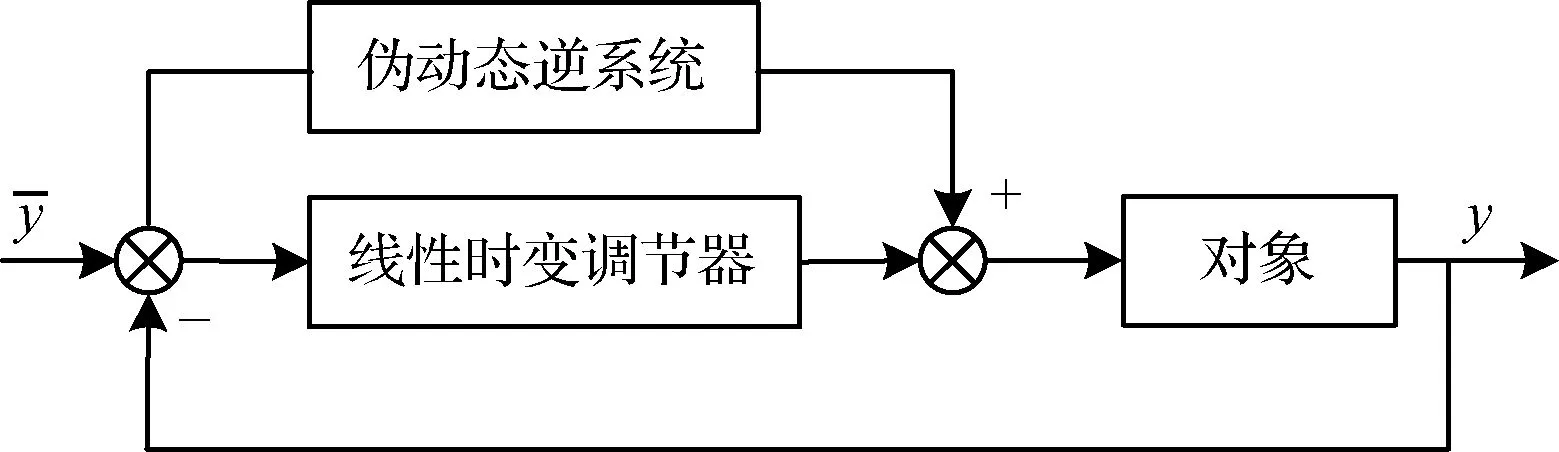
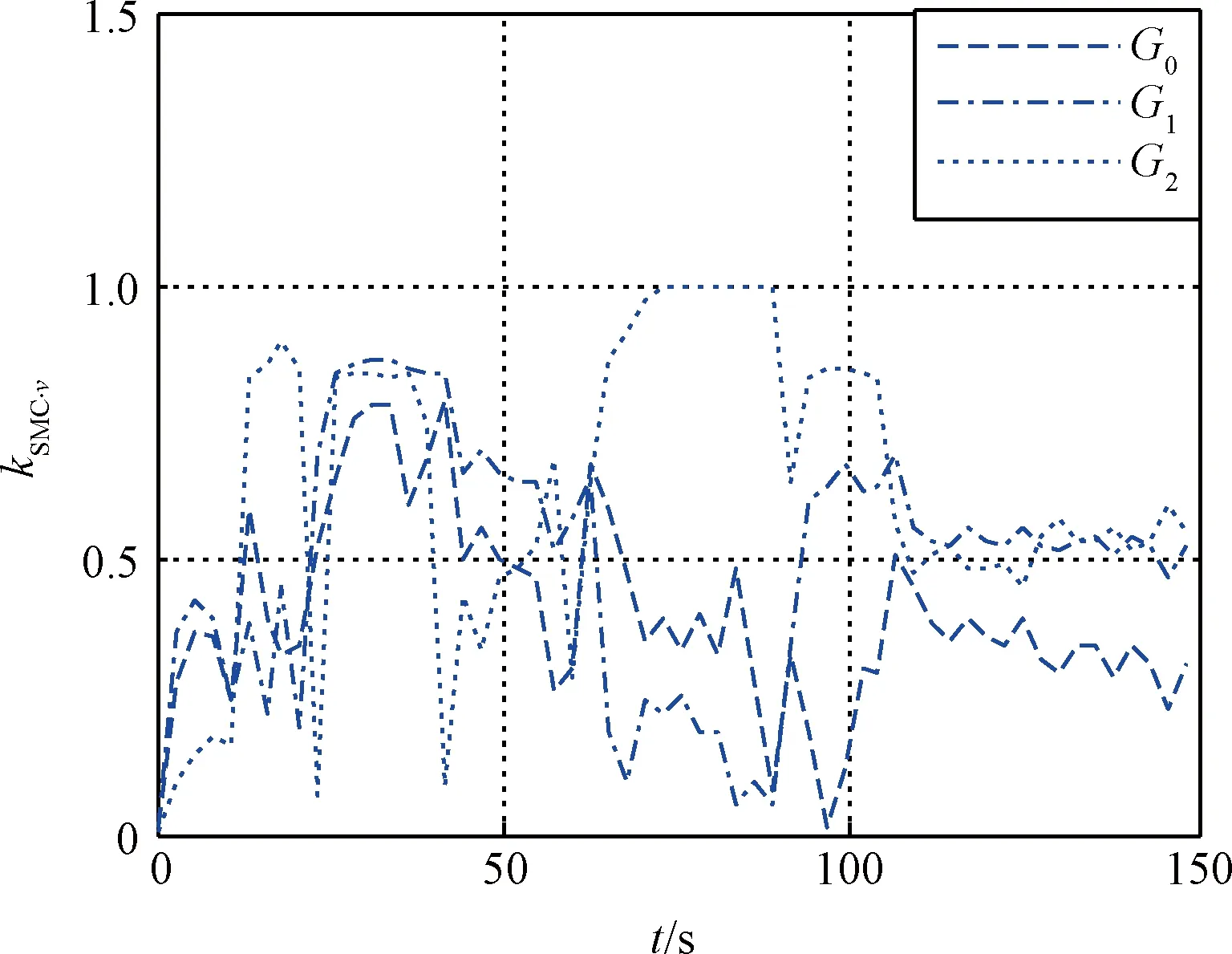
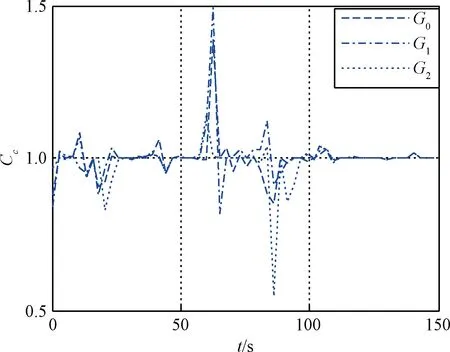
cmax<|λ1|, 0 (5) 仍以PD型滑模面为例,自适应变结构滑模面设计为[5]: (6) (7) 根据e0,结合式(5),给出正实参数ca,cb和cc的范围,可根据期望的响应特性设置。 2)滑模状态观测器 σ可以表示为: (8) (9) 式中,ci·j,∀i=1,2,3,…,m,j=-1,0,1,…,ri-2为动态性能待选参数,ei为第i个状态偏差。 微分式(9)可以得到: (10) 式中, Ξ=Ξ0+ΔΞ=[Ξ1,…,Ξm]T∈Rm (11) (12) 这里Ξ0∈Rm和ΔΞ∈Rm分别为标称和摄动干扰参量,∀i=1,2,3,…,m。式(10)~(12)导数为Lipschitz情况下导数。 假设2.基于控制能力考虑,假设ΔΞ有界: (13) (14) 为了抑制系统抖振,提高系统鲁棒性,式中ΔΞ需要通过滑模状态观测器(Sliding mode state observer, SMSO)观测得出。基于Lyapunov第二定理,设计改进型滑模状态观测器(Sliding mode district observer, SMDO)如下[11]: (15) 式中,v∈Rm为辅助控制,Γ∈Rm为辅助滑模面,λ=[λ1,λ2,…,λm]T为一常数向量且满足λi>0,∀i=1,2,3,…,m,l=[1,…,m]T为摄动干扰参量的上界。 vi=(|ΔΞi|+λi)sgn(Γi),∀i=1,2,3,…,m (16) -λi|Γi|,∀i=1,2,3,…,m (17) ∀i=1,2,3,…,m (18) (19) 综上,基于SMDO的SMC控制律为: (20) 轨迹线性化控制(Trajectory linearization control,TLC)是一种非线性跟踪和解耦控制方法,在解决强非线性快时变参数系统的控制方面具有得天独厚的优势,但在稳定性方面却因为线性化的处理,不能提供足够的鲁棒特性来满足飞行器在复杂飞行条件下的稳定控制需求,特别地对于存在大量外界干扰和建模误差且运行条件十分恶劣的实际系统,当系统中不确定性因素足够大时,TLC方法的控制性能降低甚至失效。 定理2.对于非线性系统,在x0处具有向量相对阶{r1,…,rm},则有: r1+r2+…+rm≤n (21) 若r=r1+r2+…+rm=n,系统可以实现完全I/O线性化,原输出方程可以表示为: y=BF(x)+AF(x)u (22) 根据式,若AF(x)满秩,可以构建如下的反馈控制律: (23) 使得系统实现输入输出的解耦控制。 图1 TLC方法控制结构Fig.1 The control structure of TLC 误差跟踪方程为: (24) (25) 考虑如下线性时变系统: (26) 式中: (27) 假设4.式(27)中的(A(t),B(t))可控。 基于以上假设,可设计线性时变反馈控制器η=K(t)e,使得线性时变系统平衡点e=0为指数稳定,并记Ac(t)=Ae(t)+Be(t)K(t)。式中,Ac(t)是期望的控制回路闭环误差动态特性,根据PD谱[3]进行设计。根据线性时变反馈控制律η=K(t)e可保证非线性系统在平衡点e=0指数稳定。 四强复合控制是指面向强耦合强不确定性强非线性快时变系统的复合控制。四强复合控制结构如图2所示,滑模控制(SMC)与轨迹线性化控制(TLC)组合应用,同时引入模糊控制进行双环调度,实现双环的权重智能分配。在离滑模面距离较远时,SMC环占优,充分利用SMC的适用于强耦合及强不确定性控制的优势,降低TLC的模型依赖性;在离滑模面距离较近时TLC环占优,充分利用TLC的适用强非线性、强时变特性控制的优势,削弱SMC的抖振效应,保证了工程实际应用的能力[6~11]。 图2 四强复合控制结构Fig.2 The control structure of four strong characters 四强复合控制设计的步骤可以概括为: 1)在干扰为零时,基于动态逆方法设计标称控制,基于PD谱理论设计线性时变状态反馈控制律,使得标称系统稳定。 2)设计滑模控制器和滑模观测器,逼近未知干扰,使得闭环系统具有较强的鲁棒性,在模型不确性时闭环系统稳定。 3)设计模糊决策,确定双环控制权重。 钱学森工程控制论中针对复杂系统的工程稳定性分析有如下结论[14]: 1)一般来说,采用Lyapunov方法理论上可以解决稳定性,但在实际工作中这些方法均嫌过于复杂。因为其依赖于系统系数及其基本解的一些深刻的分析特征,后者却又常常得之不易。因此该类方法没有在实际工作中得到广泛应用。 2)若系统的基本解有界,则系统稳定。只需给出n种不同的初始条件,即可求出系统的基本解。借助于主流计算机,基本解的获取比较容易,即可判别系统稳定性,不需要对系统做任何繁杂的分析。 强耦合强不确定强非线性快时变系统是一种复杂系统,考虑飞行剖面及全系统参数的不确定性,采用蒙特卡洛统计试验法获取飞行范围的基本解,钱学森全系统工程稳定性获取方法适用于该类强耦合强不确定强非线性快时变系统复合控制的稳定性分析。 飞行器数学模型如式(28)~(30)所示[15]: (28) (29) (30) 式(28)~(30)数学模型为通用数学模型,针对强耦合强不确定性强非线性快时变对象,式中的函数和参数将有所体现。具体分析如下: 1)强耦合特性 发动机与飞行器本体强耦合,主要体现在两个方面:发动机的附加力矩影响;飞行器姿态对发动机的影响。 2)强不确定特性 包括动力、气动、大气、初始状态、结构参数等多种不确定性。 3)强非线性特性 主要体现在两个方面:气动和发动机力学特性的强烈耦合在综合力学特性上表现为较大的非线性特点;飞行器跨大空域飞行条件下相对于被控对象而言,环境参数如大气密度、大气温度和风场都是非线性变化的,它们不会随时间或能量等自变量呈线性变化。 4)快时变特性 主要体现在两个方面:由于跨大空域、跨大速度的飞行轨迹特点,飞行状态参数,如飞行高度、速度和飞行器质量快速变化;飞行器自身的相关特性也不是固定不变的,主要表现为飞行器所受气动热影响效应随时间增长,相应的结构弹性同气动的耦合特性也发生变化。 基于四强控制策略的制导控制律结构如图3所示。图3中下标c表示指令值。 图3 基于四强控制策略的制导控制设计Fig.3 Control strategy based on four strong characters 受限于篇幅,这里给出制导回路的部分设计,控制回路设计思路相同。纵向制导律由滑模(SMC)制导环、轨迹线性化(TLC)制导环、模糊(Fuzzy control,FC)制导环复合而成,如式(31)所示。 uzz=kSMCuzz,SMC+kTLCuzz,TLC (31) 1)发动机保护控制SMC制导环 考虑参考轨迹跟踪及发动机保护需求,设计滑模面如式(32)所示,包括误差比例积分策略和隔离段激波串有限条件位置积分策略。 (32) uzz,SMC= (33) (34) (35) 2)TLC制导环 TLC制导环由伪动态逆控制器和线性时变调节器两部分组成。令系统摄动为零,可知制导回路系统的相对阶为2,可通过动态逆求得制导回路的控制输入: (36) 设计PI状态反馈控制律: (37) kzz(t)=[RzzBzz(t)]-1Rzz[Azz·c(t)-Azz(t)] (38) 式中:Rzz为常数阵,定义如式(39)所示,Azz为系统增广后状态方程,Azz·c为期望闭环方程。 (39) 综合式(36)和(39),可得TLC制导环控制为: (40) 3)智能权重调度策略 模糊调度流程如图4所示。 图4 模糊控制流程图Fig.4 The flow chart of fuzzy control 依据飞行器的数学模型,对所设计的基于四强控制策略的制导控制律进行数值仿真,仿真中加入静稳定度和舵效摄动,校验其鲁棒性。仿真条件详见表1。 表1 仿真条件Table 1 Description of simulation conditions 图5和图8中下标x表式参考轨迹,飞行任务为速度由Ma3加速至Ma4,高度由22.8 km爬升至27.6 km,该飞行任务跨空域、宽马赫数范围飞行,具备强耦合强不确定性强非线性快时变特征。利用基于四强控制策略的制导控制律得出的系统跟踪结果如图5~10所示。 图5 马赫数高度曲线Fig.5 Curve of height vs Mach 图6 kSMC·θ随时间变化曲线Fig.6 kSMC·θ vs time 图7 kSMC·v随时间变化曲线Fig.7 kSMC·v vs time 图8 攻角随时间变化曲线Fig.8 Angle of attack vs time 图9 飞推耦合度因子随时间变化曲线Fig.9 The coupling factor for aircraft and scramjet vs time 图10 升降舵偏转角随时间变化曲线Fig.10 Elevator rudder deflection angle vs time 从制导指令跟踪情况来看,基准弹道及摄动弹道均可精确跟踪参考轨迹的马赫数高度剖面,通过精确跟踪,可以满足马赫数、动压、热流约束要求,且为控制实现留有余量。根据kSMC·θ和kSMC·v随时间变化可知,SMC环和TLC环的控制切换权重随不确定性设置发生变化,且变化趋势与飞行器的状态密切相关。 从控制指令跟踪情况来看,基准弹道及摄动弹道攻角及攻角变化率满足约束要求。 飞推耦合度因子Cc,定义如式(41)所示。该因子表征飞推力矩耦合程度,其数值越大,则耦合程度越强。 (41) 根据飞推耦合度因子随时间变化可知,发动机附加力矩占比较大,且其大小与飞行器的状态密切相关,对飞行器姿态控制提出了较高要求。对于基准弹道攻角可精确跟踪攻角指令,对于摄动弹道,随着舵效减小,静稳定度增大,攻角跟踪精度变差,当摄动程度为30%时,攻角跟踪精度在0.5°以内,同时舵面偏转角度增大。 考虑初始状态散布,同时附加发动机推力、附加力矩、飞行器升力阻力、压心及舵效不确定性,进行500条次蒙特卡洛仿真,统计飞行过程中约束满足情况,最大过载变化范围[-1, 3.3]g,最大攻角变化范围[4, 7.3]°,角速率变化范围[-0.4, 2.7]°/s。受限于篇幅,给出最大攻角散布示意图,如图11所示,飞行范围内基本解有界,采用钱学森全系统工程稳定性获取方法可证明飞行范围内的稳定性。 图11 蒙特卡洛弹道最大攻角散布Fig.11 The max angle of attack spread 随着飞行器的跨空域、宽马赫数范围飞行,飞行器显现出强耦合强不确定性强非线性快时变特性,对控制提出了非常高的要求。单一控制方法难以兼顾全部控制需求,提出一种该复合控制方法,由三个核心模块组成,依次为强耦合强不确定性控制模块、强非线性快时变控制模块、智能调度模块。强耦合强不确定性控制模块采用自适应变结构和滑模观测器策略,强非线性快时变控制模块采用轨迹线性化策略,智能调度模块采用模糊策略。以一具备典型四强特征的飞行器为例,进行了对象四强特性分析,在此基础上采用四强复合控制方法设计了制导律和控制律,仿真结果表明,该方法有效、可靠,采用钱学森全系统工程稳定性获取方法可证明飞行范围内的稳定性。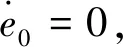


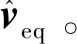
1.3 基于强非线性快时变控制




1.4 四强复合控制

2 典型强耦合强不确定性强非线性快时变飞行器控制
2.1 对象模型


2.2 对象特性分析
2.3 四强复合控制设计
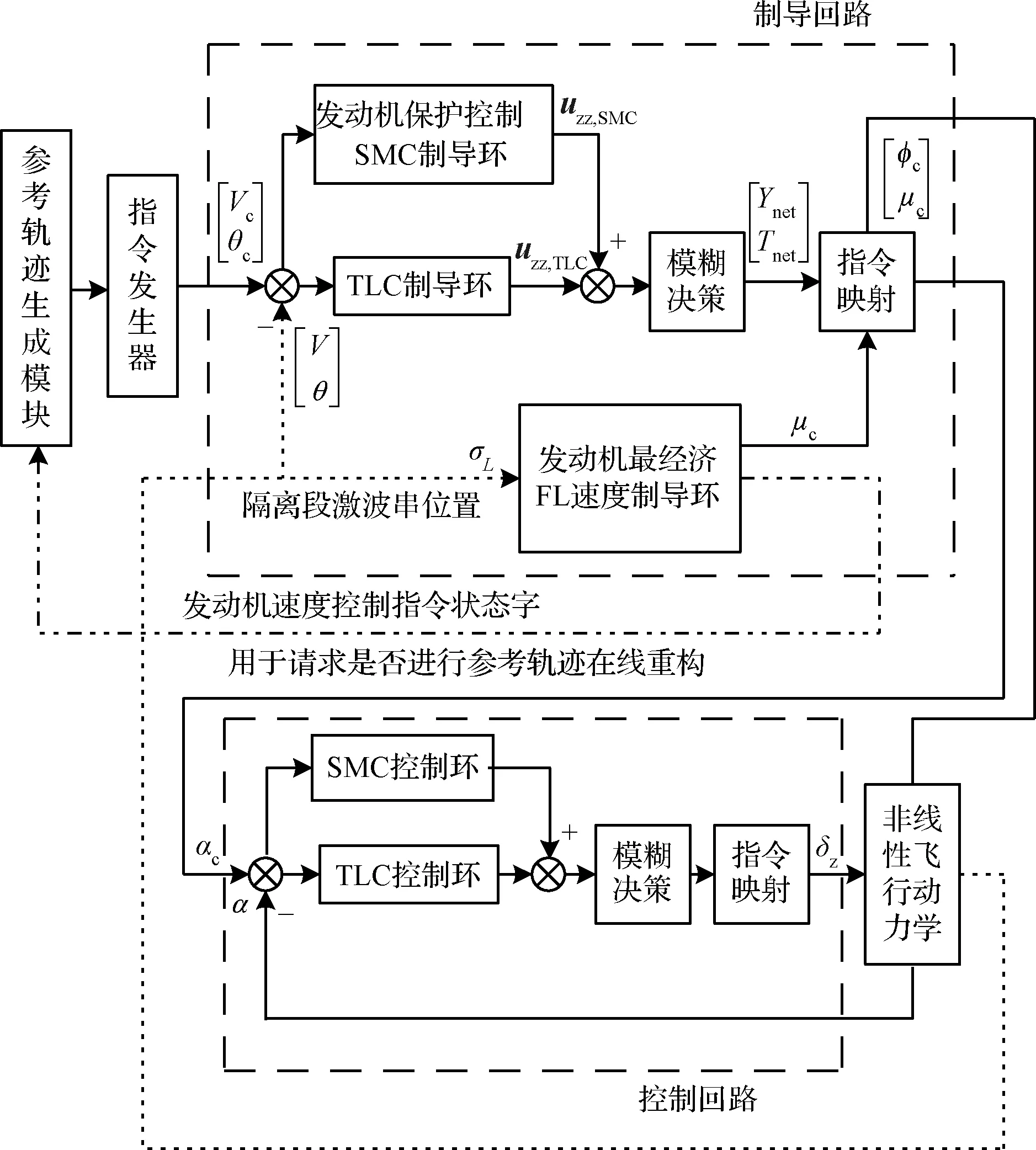







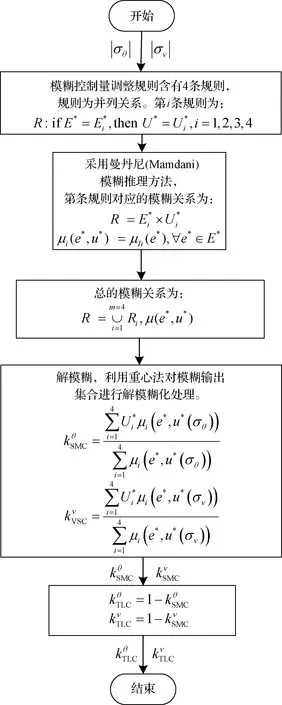
3 仿真校验







4 结 论
