星箭连接界面处环形分布动载荷识别

尹 健，吴邵庆，陈树海

(1. 东南大学工程力学系，南京 210096；2. 东南大学空天机械动力学研究所，南京 211189；3. 上海卫星工程研究所，上海 201109)

0 引 言

卫星等航天器所受到的动态载荷信息是其结构设计的关键，获取精确的动态载荷在航天工程实践与研究中具有重要的意义。火箭与卫星之间常采用包带连接结构，其连接性能将影响星箭系统的动力学特性，因此星箭连接动力学问题受到广泛关注[1]。火箭发射过程中会受到横向载荷的作用，在星箭连接界面上产生弯矩和剪力，使得星箭连接处的动载荷呈现环形且非均匀分布的特征。由于技术与成本限制，往往难以通过直接测量获取动载荷信息。而动载荷间接识别技术可以作为星箭界面动载荷获取的手段，即利用可以准确测量获取的卫星结构动响应来反演卫星结构所受的环形分布动载荷。

根据动载荷的特征，动载荷识别方法可以划分为集中动载荷识别方法和分布动载荷识别方法。集中动载荷识别方法主要包括频域法和时域法。频域法是基于离散物理空间或者模态空间内的结构动力学方程，在频域内根据系统的频率响应函数与响应频谱之间的关系来识别动态载荷[2-3]。频域法要求测量数据的样本具有一定的长度，故一般只适用于稳态或平稳随机动载荷的识别，对瞬态冲击或非平稳随机动载荷的识别有较大局限性。与频域方法相比，时域法在考虑时变特征等方面具有一定的优势，其反求结果精度较高[4]。经典时域法是在模态空间内利用杜哈梅积分构建响应与载荷的关系，反演动态载荷；在此基础上，进一步发展了基于正交基模型的识别方法[5-6]等。Wu和Law[7-8]则对不确定性动载荷的识别进行了研究。作为反问题，动载荷识别存在不适定性的问题，针对此问题，在经典的Tikhonov正则化方法的基础上，Qiao等[9]提出了基于稀疏反卷积模型的PDIPM(Primal-Dual Interior Point Method)法，对冲击载荷进行了识别。近年来，不少学者将动载荷识别方法应用于飞行器的动弯矩识别中[10-11],为飞行器设计提供了宝贵的载荷信息。

对于分布动载荷，虽然其识别方法与集中动载荷识别方法有相通之处，但由于要同时获取动载荷的空间分布形式以及随时间变化的规律，其识别难度较大。秦远田等[12]提出了基于广义正交多项式的分布动载荷识别方法，并将该方法应用于梁板结构的分布动载荷识别；Jiang和Hu[13]基于Legendre多项式对动载荷的空间分布函数进行正交展开，对薄板上的分布动载荷进行了识别。Li等[14]基于分布动载荷的空间分布与时间历程可解耦的假设，利用脉冲响应函数与Chebyshev正交多项式对分布动载荷进行了识别。

目前，识别分布动载荷的思路一般是基于集中动载荷的识别方法，通过引入正交基函数来拟合动载荷的空间分布，将连续分布的动载荷识别问题降阶为有限个参数的识别问题。但仍然存在以下问题：首先，在动载荷分布特征未知的情况下，拟合空间分布函数的正交多项式阶数难以确定；其次，正交基函数是一种全局基函数，针对具有局部突变分布特征的动载荷难以精确识别；最后，对于具有周期性特征的环形分布动载荷，用正交多项式来拟合动载荷的空间分布，无法保证环形动载荷分布的首尾连续性，亦不能保证动载荷分布函数导数的连续性。为改进基于正交多项式的分布动载荷识别方法存在的问题，本文提出基于B样条基函数的环形分布动载荷识别方法。由于B样条函数的分段、高阶导数连续等特性，识别出的分布动载荷能同时保证识别效率与精度。最后，将本文提出的识别方法应用于卫星结构星箭界面动载荷识别。

1 动载荷识别原理

1.1 基于脉冲响应函数的动载荷识别

在时域内，若用脉冲信号作为单元信号，可将动态载荷表示为一系列脉冲函数的叠加。当线性系统在连续时间域内只受到单源载荷时，系统的响应在时域内可以表示成如下激励与脉冲响应函数的卷积分的形式：

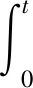
(1)

式中：y(t)为结构上测点处的响应，q(τ)是载荷的时间历程，g(t-τ)为载荷作用点到结构上响应测点的单位脉冲响应。

将式(1)中的卷积分在时间域内用m个等间隔的采样点进行离散，可转化为一组线性方程组：

(2)

式中：yi，gi，qi分别为t=iΔt时刻结构的响应、脉冲响应函数和待识别的载荷；Δt为离散的采样时间间隔；m为采样点的数目。将式(2)表示为如下矩阵形式：

Y=GQ

(3)

式中：Y为结构响应yi组成的列矩阵，G为脉冲响应函数gi组成的脉冲响应函数矩阵，Q为待识别载荷qiΔt组成的列矩阵。

对于多源载荷，类似于单源载荷作用下的推导过程，依据叠加原理，可将多源载荷问题表示为如下矩阵形式：

(4)

式中：m表示响应测点个数，n表示待识别载荷的个数；Yi为第i个测点的响应组成的列矩阵；Qj为第j个待识别载荷在采样点处的值qj,kΔt组成的列矩阵；Gi,j为第j个待识别载荷作用点到第i个测点的脉冲响应矩阵。

1.2 B样条基函数

在区间[x0,xn)上，k次B样条基函数的递推定义如下：

(5)

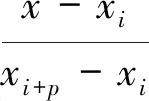
(6)

式(5)～(6)通常称为Cox-de Boor递归公式，其中，p为B样条基函数的次数；Ni,p(x)是第i个p次的B样条基函数；xi为节点。

由于三次B样条函数具有二阶导数连续的性质，因此本文的研究中选用三次B样条基函数，其形式如图1所示，则B样条函数可拟合为：

(7)

图1 三次B样条基函数Fig.1 Basis function of cubic B-spline

1.3 环形分布动载荷识别

对于环形分布载荷，考虑周期性边界条件，其空间分布可通过B样条基函数表示为：

(8)

式中：B(x)为环形分布式动载荷的空间分布，Ni,p(x)为第i个p次B样条基函数，Bi为第i个p次B样条基函数的系数，N为基函数个数。

作用在结构上的环形分布式动载荷q(x,t)可以表示为：

q(x,t)=B(x)s(t)

(9)

式中：s(t)表示随时间变化的动载荷。

将式(8)代入式(9)，可将环形分布式动载荷q(x,t)表示为：

(10)

结合有限元模型，针对图2中的环形分布动载荷，将动载荷的分布函数沿环划分为N段，设置N个控制节点，将两个控制点之间的部分继续划分为多个单元，有限元节点总数为n个。如图2所示，将动载荷分布函数沿环形划分为8段，则N=8。在确定B样条基函数次数及控制点个数之后，基函数形式亦随之确定。假设共选取m个测点获取响应信息。

图2 B样条基函数形式的脉冲激励Fig.2 The B-spline basis impulse excitation

利用有限元方法，通过形函数积分可将分布式动载荷q(x,t)转化为结构的单元节点载荷Fe(t)：

(11)

式中：Ne(x)为单元形函数。

将式(10)代入式(11)，节点载荷可表示为：

(12)

则节点载荷向量可表示为：

(13)

依据第1.1节的动载荷识别理论，在多源载荷作用下，结构测点响应可表示为：

(14)

式中：fj(τ)为第j个节点载荷的时间历程，gk,j(t-τ)为从第j个激励节点到第k个响应测点的脉冲响应函数，n为动载荷环形分布的有限元节点数。

将式(13)代入式(14)可得：

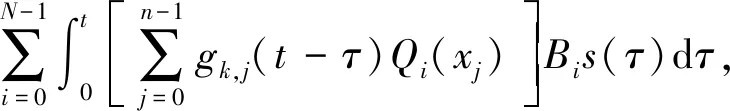
k=1,2,…,m

(15)

式中：Qi(xj)为第i个B样条基函数形式的分布载荷经有限元方法转化后的第j个节点上的载荷。

记

(16)

则式(15)可转化为

(17)

式中：Gk,i(t-τ)为在结构上作用第i个B样条基函数分布形式的脉冲激励后(见图2)测点k处所得到的脉冲响应函数。

式(17)可表示为如下矩阵形式：

(18)

式中：yk，si分别表示第k个测点处响应yk和第i个控制点处激励si在各时间点的值所组成的列矩阵；Gk,i是结构在第i个p次B样条基函数Ni,p形式的脉冲激励作用下，第k个测点处得到的脉冲响应函数所组成的脉冲响应矩阵。

式(18)可简化为：

Y=GBs

(19)

式中：Y为m个测点的加速度响应yk组成的列矩阵，G为脉冲响应矩阵组装成的传递矩阵，Bs为样条基函数系数Bi与激励在各时间点的值si的乘积组成的列矩阵。

利用最小二乘法，得到实测加速度响应与基础加速度激励的关系为：

Bs=(GTG)-1GTY

(20)

在动载荷识别过程中，矩阵G的病态可能引起式(20)求解结果的较大误差，可利用正则化方法来提高求解精度。

基于B样条函数的分布动载荷识别步骤为：

(1)确定B样条基函数次数p(阶数p+1)及环形分布动载荷作用处的分段数(控制点数)，由递归公式(5)～(6)确定B样条基函数的函数形式Ni,p。

(2)在结构上分别施加各段B样条基函数形式的脉冲激励，得到测点的脉冲响应函数，组装获得式(19)中的传递矩阵G。

(3)根据式(20)，由测点加速度响应y反演B样条基函数系数Bi与基础激励时程s(t)的乘积。

(4)由式(10)重构获得环形分布动载荷q(x,t)。

2 算例研究

为校验本文提出的方法，针对尺寸和材料参数如表1所示的某卫星结构，建立如图3所示有限元模型，开展数值仿真研究。卫星底座处受到环形分布动载荷激励，其有限元网格以及节点及控制点编号情况如图4所示。

图3 卫星有限元模型Fig.3 Finite element model of satellite

表1 卫星模型尺寸及材料参数Table 1 Dimension and material parameters of satellite model

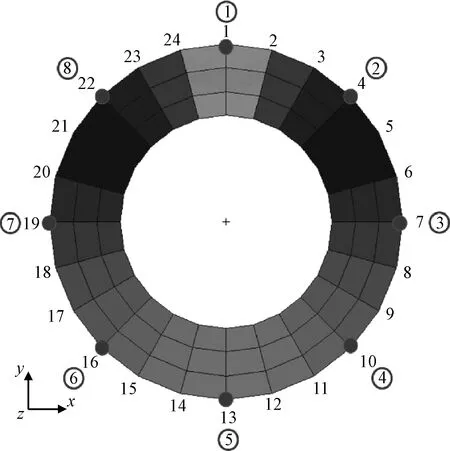
图4 节点与控制点排布及编号Fig.4 Arrangement and number of nodes and control points

卫星有限元模型所在坐标系如图3所示，在底部施加约束，仅释放z方向的平动自由度。卫星结构上的响应测点选取对动载荷识别结果有重要影响，因此需要通过频响分析，选择对底部加速度激励敏感的测点。在底部施加单位频域加速度激励，频率范围为0～100 Hz，能够覆盖模型前10阶固有频率，获得卫星结构的加速度频率响应云图(见图5)，图5中给出了卫星模型一阶频率附近4 Hz处的频率响应云图。在频率响应云图数值较大处，如上、下盖板以及承力筒上布置测点，测点编号及位置如图5所示。

动载荷识别仿真研究中，需要测点的加速度响应作为输入数据。加速度响应的计算方法如下：在卫星底部作用一沿环形分布的基础加速度激励q(x,t)，其中B(x)为基础加速度激励的空间分布函数，有

(21)

图5 4 Hz处(模型一阶固有频率)频率响应云图Fig.5 Cloud chart of frequency response at 4 Hz (first order natural frequency of model)

s(t)为分布动载荷的时变分量，在本节算例中，依据高斯随机过程的功率谱获得s(t)的时程曲线：

(22)

式中：Δω表示频率增量；ωk=ωmin+Δω(k-1)；Nk表示区间[ωmin,ωmax]上频率划分的总个数，Nk=(ωmax-ωmin)/Δω；ψk表示均匀分布于区间[0,2π]内的随机相位角；Φ(ω)表示零均值非平稳高斯随机过程的双边功率谱密度函数，有如下定义：Φ(ω)=(1/2π)(2/ω2+1)，具体参数设置如表2所示。

卫星结构加速度响应分析时长为0.5 s，步长为0.0005 s，施加于图3中有限元模型底部z方向，得到结构上各测点处的加速度响应。利用仿真得到的各测点处的加速度响应，根据第1.3节中的动载荷识别步骤，开展卫星结构底部环形分布加速度激励的识别。在求解式(20)时，采用Tikhonov正则化方法提高列矩阵Bs求解精度，采用广义交叉验证准则确定最优正则化参数。

表2 s(t)时程曲线的参数设置Table 2 Parameter settings for the time history of s(t)

为了定量给出基础加速度激励时程的识别精度，引入对数相对误差计算公式：

(23)

式中：Ai,C为识别加速度激励的第i个峰值，Ai,E为参考加速度激励的第i个峰值；n为峰值个数。

为了定量给出基础加速度激励空间分布的识别精度，引入相对误差计算公式：

(24)

2.1 无测量噪声情况下的识别结果

将动载荷分布函数沿环划分为8段，设置8个控制节点，控制点位置及有限元节点编号如图4所示，确定B样条基函数形式；在结构上选取8个测点，由测点处加速度响应反演得到卫星底座处各节点的基础加速度激励时程曲线及激励的空间分布。某节点处基础加速度激励识别结果如图6～7所示，识别误差如表3所示。

表3 各节点基础加速度激励识别误差Table 3 Identification error of base acceleration excitation at each node

从图6～7和表3可以看出，在无噪声情况下，各节点处基础加速度激励识别结果非常准确，平均峰值误差为0.122 dB；基础加速度激励的空间分布识别的误差为5.37%，误差较小，表明本文提出的环形分布动载荷识别方法具有可行性。

2.2 测量噪声对识别结果的影响

在控制点数及测点数均与第2.1节相同的情况下，在卫星结构加速度响应中分别加入10%和15%的噪声，开展测量噪声对动载荷识别结果的影响研究。噪声施加方式为：

Yerr=Ycal+lnoisestd(Ycal)rand(-1,1)

(25)

式中:Ycal是计算得到的位移响应；std(Ycal)是计算的位移响应的标准差；lnoise是个百分数，代表噪声水平；rand(-1,1)是[-1,1]之间的随机数。

由测点加速度响应反演得到卫星底座处各节点的基础加速度激励时程曲线。图8、图9分别给出了在不同噪声水平下基础加速度激励时程识别值与参考值对比，识别误差如表4所示。

图8 节点4处加速度识别值参考值对比(10%噪声水平)Fig.8 Comparison of identified and referenced base acceleration excitation at node 4(10% noise level)

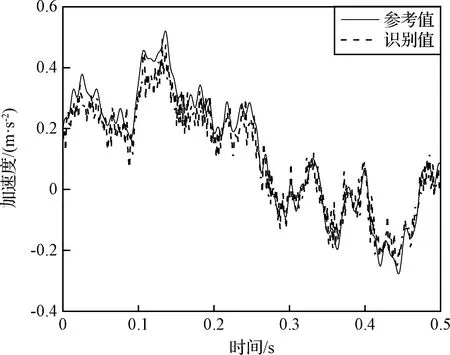
图9 节点4处加速度识别值参考值对比(15%噪声水平)Fig.9 Comparison of identified and referenced acceleration excitation at node 4(15% noise level)

表4 不同噪声水平下基础加速度激励识别误差Table 4 Identification error of base acceleration excitation under different noise levels

从图6、图8～9和表4可以看出，随着噪声水平的提高，载荷识别的精度有所下降，但在噪声水平比较高的情况下，基础加速度激励的时间历程依然能被比较准确地重构出来，节点平均峰值误差小于1.5 dB，说明本文所述的计算方法能抑制噪声对载荷识别结果的影响，具有较好地稳定性。

2.3 测点数对识别结果的影响

在控制点数与第2.1节相同的情况下，依据图5中由频响函数值选择测点的方法，在结构上分别选取不同的测点数目，在10%噪声水平下，由测点加速度响应反演得到卫星底座处各节点的基础加速度激励时程曲线及空间分布。图10～13给出了不同测点数下基础加速度激励时程及空间分布的识别值与参考值对比，识别误差如表5所示。

图10 节点4处加速度识别值与参考值对比(12测点)Fig.10 Comparison of identified and referenced acceleration excitation at node 4(12 measurement points)

图11 节点4处加速度识别值与参考值对比(16测点)Fig.11 Comparison of identified and referenced acceleration excitation at node 4(16 measurement points)

从图8、图10～13和表5可以看出，在控制点数一定的情况下，当满足测点个数大于或等于待识别B样条基函数系数个数的条件时，三种工况下动载荷时间历程识别的平均峰值误差小于1 dB，动载荷空间分布识别的误差小于6%，均能较为准确地重构出环形分布动载荷的时间历程与空间分布，表明本文方法可以在使用少量测点的条件下保证动载荷识别的精度。

图12 加速度激励空间分布识别值参考值对比(12测点)Fig.12 Comparison of identified and referenced spatial distribution of acceleration excitation(12 measurement points)

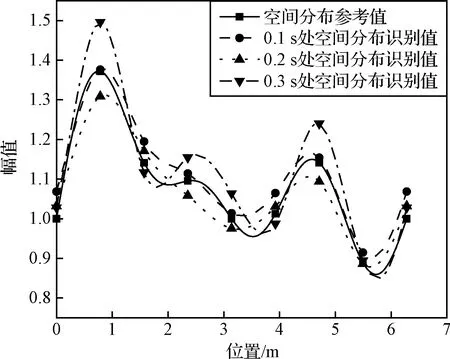
图13 加速度激励空间分布识别值参考值对比(16测点)Fig.13 Comparison of identified and referenced spatial distribution of acceleration excitation(16 measurement points)

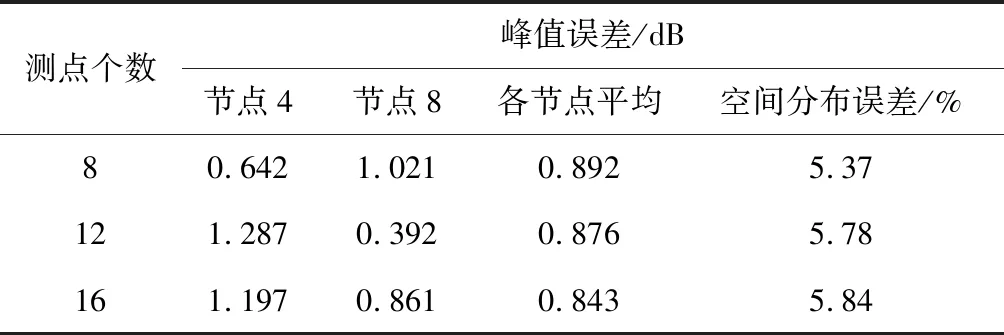
表5 不同测点数下基础加速度激励识别误差Table 5 Identification error of base acceleration excitation of different number of measurement points

2.4 控制点数对识别结果的影响

根据图4等分动载荷分布函数的方法，分别在卫星底部选择不同的控制点数目，分别确定B样条基函数表达式，在10%噪声水平下，由测点加速度响应反演得到卫星底座处各节点的基础加速度激励时程曲线及空间分布。图14～17分别给出了在不同控制点数下基础加速度激励时程及空间分布的识别值与参考值对比，识别误差如表6所示。

从图8、图14～17和表6可以看出，在本算例中，如选择6个控制点，动载荷的空间分布识别误差超过了10%；当控制点数增加至8以上时，动载荷识别的精度显著提高，空间分布的识别误差低于6%，节点的平均峰值误差小于1 dB，表明控制点数的增加可以有效提高环形分布动载荷的时间历程与空间分布的识别精度。

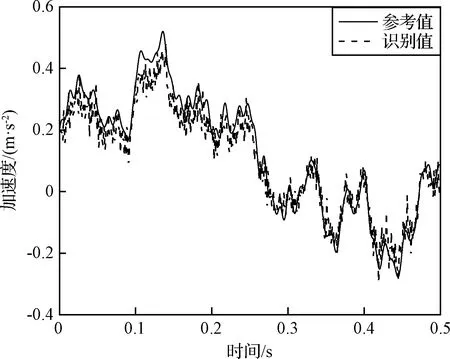
图14 节点4处加速度识别值参考值对比(6控制点)Fig.14 Comparison of identified and referenced acceleration excitation at node 4(6 control points)

图15 节点4处加速度识别值参考值对比(12控制点)Fig.15 Comparison of identified and referenced acceleration excitation at node 4(12 control points)

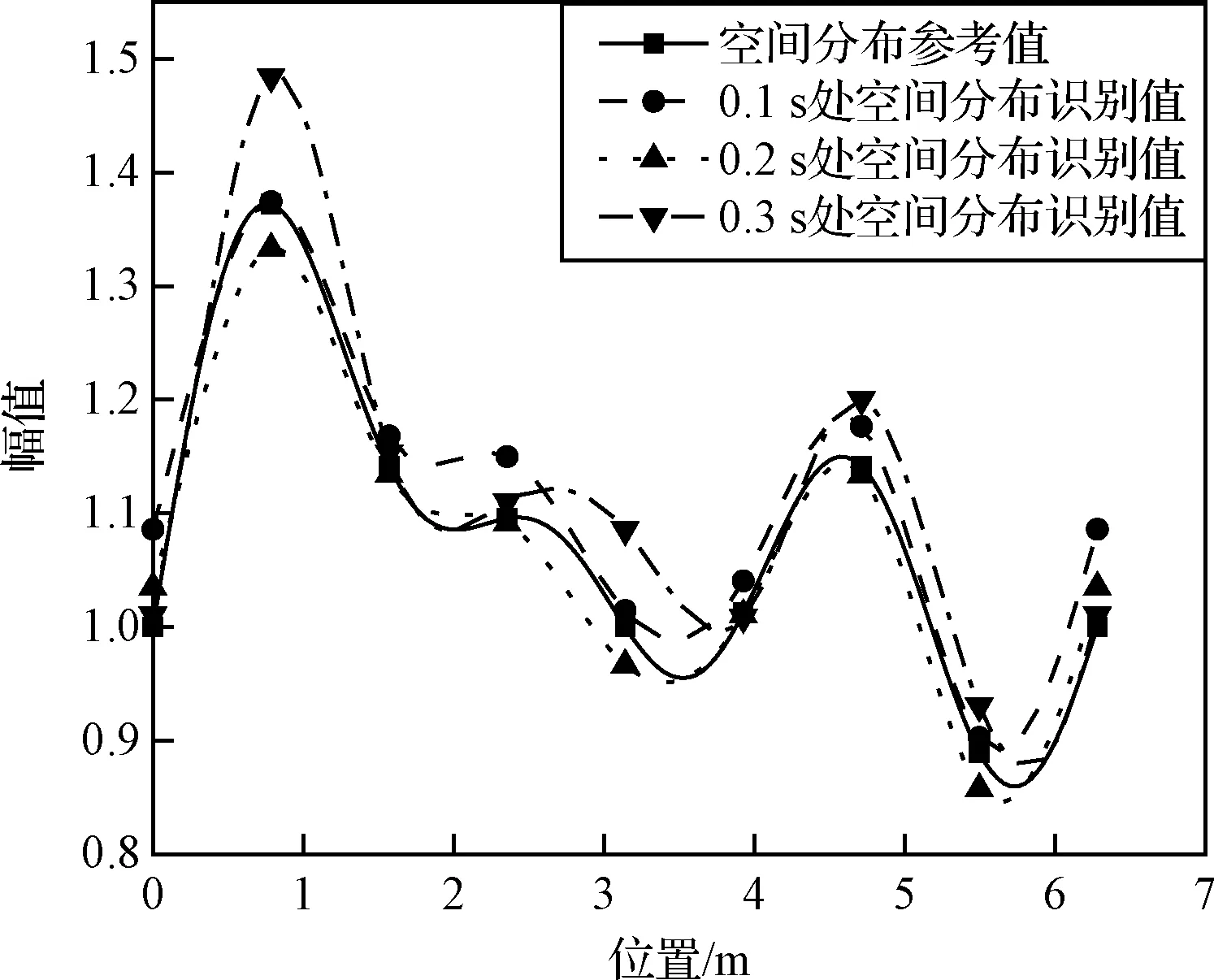
图16 加速度激励空间分布识别值参考值对比(8控制点)Fig.16 Comparison of identified and referenced spatial distribution of acceleration excitation(8 control points)

图17 加速度激励空间分布识别值参考值对比(12控制点)Fig.17 Comparison of identified and referenced spatial distribution of acceleration excitation(12 control points)

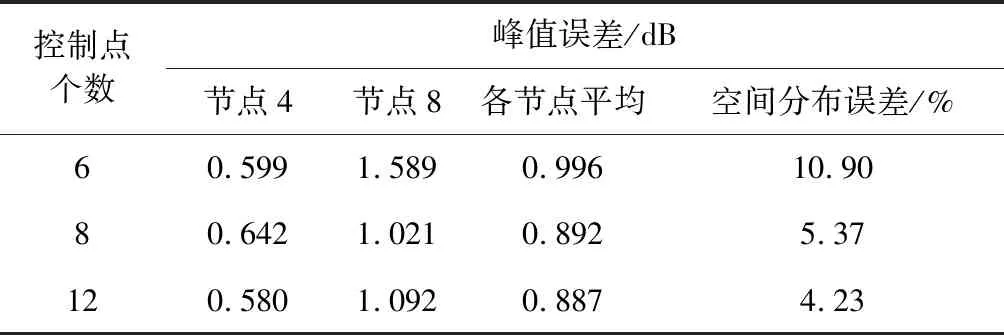
表6 不同控制点数下基础加速度激励识别误差Table 6 Identification error of base acceleration excitation of different number of control points

3 结 论

本文用B样条函数表示动载荷分布函数，提出一种环形分布动载荷的识别方法，并将该方法应用于卫星结构底座处星箭连接界面的动载荷识别。对识别方法开展数值仿真研究，校验了该识别方法的有效性，讨论不同测量噪声水平，测点数，B样条控制点数等因素对动载荷时程以及空间分布识别结果的影响，结果表明：

1)噪声对动载荷识别精度有一定的影响，由于B样条本身具有平滑特性，本文的动载荷识别方法对响应中的测量噪声具有较好的鲁棒性。

2)在控制点数与噪声水平一定的情况下，当满足测点个数不小于待识别B样条基函数系数个数的条件时，较少的测点数目即可保证动载荷识别结果的精度。

3)在噪声水平一定的情况下，增加控制点数，可以有效提高动载荷的识别精度，特别是动载荷分布函数识别结果的精度。

对于具有周期性特征的环形分布动载荷，本文提出的方法能保证识别出的动载荷空间分布的首尾连续性，也能保证动载荷空间分布函数导数的连续性；相比传统的识别方法，能减少测点数，降低矩阵的维数，减小反问题计算过程中矩阵的病态性，识别效率和精度较高。本文方法中，关于B样条基函数次数及控制点数量的确定准则，还值得进一步研究。