基于空间多点输入的LSSVM非高斯风压预测

楼志挺,李春祥

(上海大学土木工程系,上海200444)

风荷载是建筑设计、施工及运营使用阶段影响结构安全的重要因素.对于建筑表面的风荷载,特别是非高斯性较强的脉动风,将可能使建筑物发生较大的风致振动,从而影响其正常使用[1].因此,对非高斯较强的脉动风压进行研究至关重要.目前,获取风压的方式主要有数值模拟、风洞试验以及现场实测,其中现场实测是研究风场特性最为真实和直接的手段.但是现场实测方法由于其操作困难,耗时耗资太大,只能针对有限的建筑结构等缺陷限制着它的使用.因此,风压预测是一种非常有效的方法.

目前,基于数据驱动技术的预测方法[2-6]被大量地应用在许多领域.风压预测大致可分为利用历史风压数据预测未来风压数据和利用周边空间点的风压数据预测未知空间点的风压数据,前者主要利用风压在时间上的自相关性,后者主要利用风压的空间相关性.对于利用空间相关性的风压预测,迟恩楠等[7]等进行了研究,但都基于两个空间点预测一个空间点.本工作为提高预测精度,进行基于最小二乘支持向量机的采用4个空间点预测一个空间点的预测方法,分别进行内插预测和外插预测.

1 风压数据

本工作中的风压数据来源于李锦华等[8]对某地一矩形建筑进行的现场实测,记录了2012年11月23日300 min的风压时程数据.矩形建筑实测点布置如图1所示,沿AB墙面竖直方向等间距布置5个测点编号为1#∼5#,AD墙面竖直方向等间距布置5个测点编号为6#∼10#,其中AD为迎风面,AB为背风面.由于背风侧风压的非高斯性比迎风侧强[8],故本工作选取采样频率为1 Hz的背风侧实测风压为原始数据,时长取1 000(1 000个数据点)、1 600 s(1 600个数据点)两种.5个测点的两种时长的风压时程如图2所示.

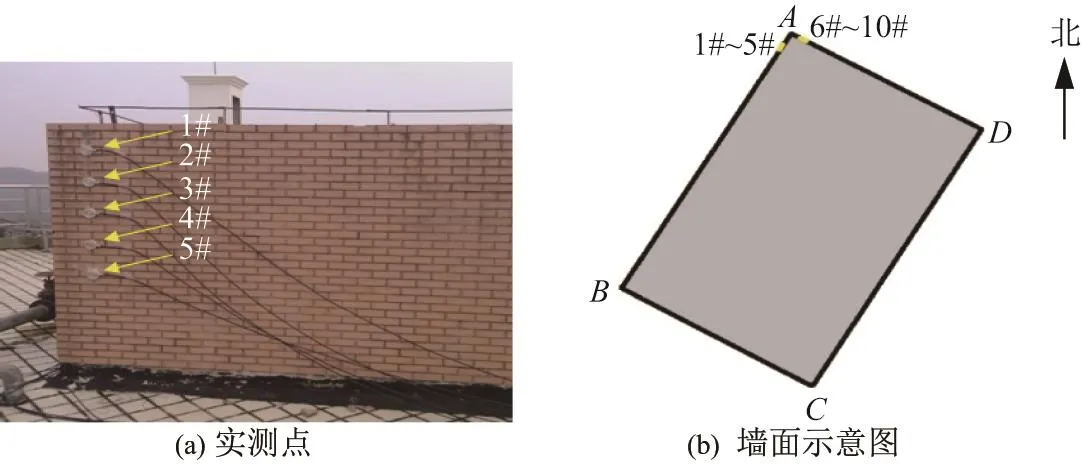
图1 矩形建筑实测点布置Fig.1 Layout of measuring points of rectangular building

2 最小二乘支持向量机

目前,主流的预测工具有神经网络和支持向量机,其中神经网络追求经验风险最小化,而支持向量机追求结构风险最小化,因此支持向量机具有更好的泛化能力.但是,支持向量机也具有自身的缺陷,即计算复杂、收敛速度慢.为此,1999年Suyken等[9]提出了最小二乘支持向量机(least square support vector machine,LSSVM)的概念,其原理如下.

对于一组给定的训练样本集T={(xi,yi)|xi∈Rn,yi∈R,i=1,2,···,t},其中xi为输入向量,yi为相应的目标输出.假设其回归函数为

式中,ϕ(x)为映射函数,ω为权向量,b为偏置.

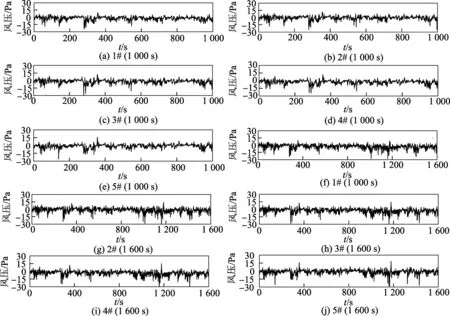
图2 两种时长的原始风压时程图Fig.2 Time history of initial wind pressures of two different lengths

基于结构风险最小化原则,回归函数可以转换为

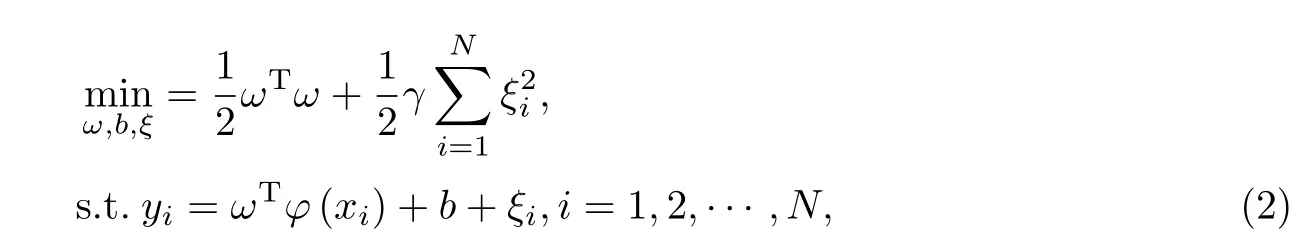
式中,γ为正则化参数且γ>0,ξi为松弛因子.

引入Lagrange乘数法,得到

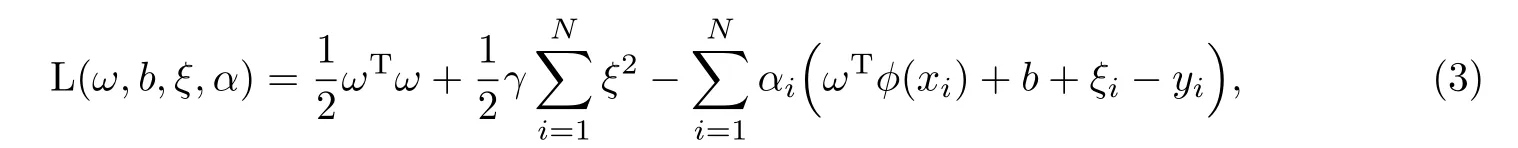
式中,αi为Lagrange乘子,其值可根据KKT优化条件,分别对ω,b,ξ,α求偏导并令偏导数为0获得.最后建立最终的回归函数

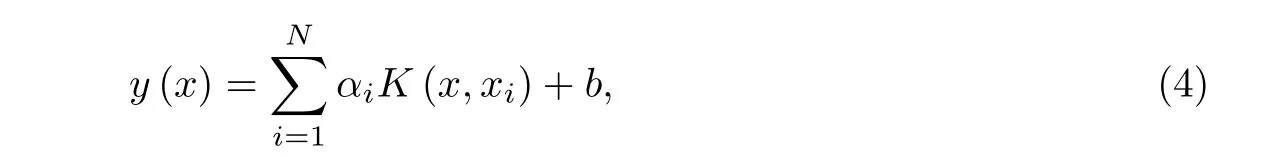
式中,K(x,xi)为核函数.鉴于径向基核函数结构形式简单,光滑性好以及泛化能力强,本工作选择径向基核函数作为LSSVM的核函数,其表达式为

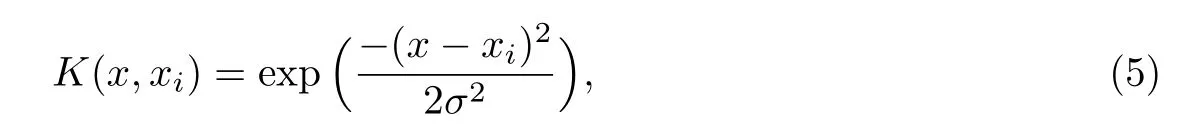
式中,σ为核函数的宽度.

3 智能优化算法

本工作中的LSSVM选用径向基核函数作为核函数,故有2个待定参数,分别是正则化参数γ和核函数参数σ.由于不同参数组合(γ,σ)对LSSVM的预测性能有影响,故需选出合适的参数组合.本工作采用粒子群算法和布谷鸟算法进行参数寻优,且适应度函数均采用

式中,yi为第i个样本的实际值,b yi为第i个样本的预测值.

3.1 粒子群算法

粒子群算法(particle swarm optimization,PSO)[10]由Kennedy等提出,其特点是结构简单、迭代时间短,其原理如下.假设在一个N维的目标搜索空间中,有m个粒子组成一个群落.第i个粒子所在的位置用一个N 维向量表示,记为xi=(xi1,xi2,···,xiN),i=1,2,···,m.第i个粒子的飞行速度也用一个N 维向量表示,记为vi=(vi1,vi2,···,viN),i=1,2,···,m.每一个粒子都是一个潜在解,对于第i个粒子,将xi带入目标函数求得其适应度值,然后根据适应度值衡量xi的优劣,并记录其历史最好位置,记为pi=(pi1,pi2,···,piN),i=1,2,···,m.pi也称为个体极值pbest.目前为止,整个群体中所有粒子发现的最好位置记为pg=(g1,g2,···,gN),pg也称为全局极值gbest.粒子的飞行速度和位置按下式更新:

参照附录A归档章示例，保管期限的标识方式有两种：一种是分别以代码“Y”“D30”“D10”标识，另一种则可以使用“永久”“30年”“10年”简称标识。对比两种标识，前者方便、简洁；而后者则更为清晰，便于非专业档案人员理解。总体而言，两者均有其特点，档案人员可以根据自身编制习惯及工作实际进行选择，但必须保持标识的总体一致性。

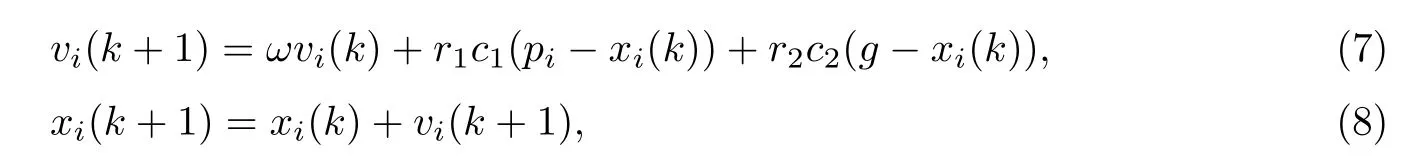
式中:i=1,2,···,m,m表示种群中粒子的总个数;r1,r2表示[0,1]之间的随机数;c1,c2表示权重因子;ω表示惯性权重函数.

3.2 布谷鸟搜索算法

布谷鸟搜索(Cuckoo search,CS)算法[11]由剑桥大学Yang等提出,其特点是参数少、操作简单、易实现、随机搜索路径优和寻优能力强.布谷鸟搜索算法的原理如下:先随机产生n个N 维的鸟巢的初始位置nesti=(nesti1,nesti2,···,nestiN),i=1,2,···,n; 利用适应度函数计算每个鸟窝位置的适应度值,并设置好最大发现概率pa和最大迭代次数等参数;然后,利用莱维飞行搜索新的鸟巢位置,并计算适应度值与历史最优鸟巢位置的适应度值进行比较,选出当前最优的鸟巢位置;随后在区间[0,1]产生一个随机数r,并与pa(寄生巢的主人发现外来蛋的概率)进行比较,若r>pa,则对nesti进行随机改变,反之不变;最后,保留最好的一组鸟巢位置.莱维飞行位置按下式更新:

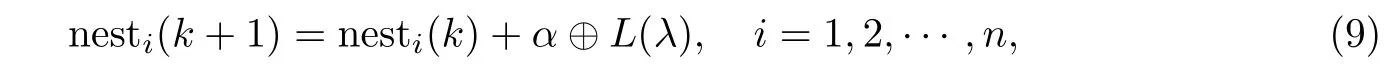
式中:nesti(k)表示第i个鸟巢在第k代的位置;⊕表示点对点乘法;α表示步长控制量,用于控制步长的搜索范围,其值服从正态分布;L(λ)为L´evy随机搜索路径,随机步长的分布为L´evy分布,即

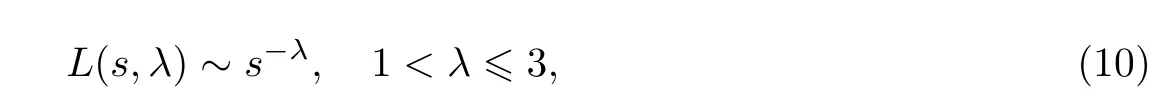
式中,s表示由莱维飞行得到的随机步长.

4 风压预测与结果分析

利用LSSVM对实测风压进行预测,其中LSSVM的参数组合(γ,σ)采用PSO,CS寻优.预测分为内插预测以及外插预测,其中内插预测又分为2#,4#测点预测3#测点,1#,2#,4#,5#测点预测3#测点;外插预测分为2#,3#测点预测1#测点,2#,3#,4#,5#预测1#测点.此外,本工作中训练集与测试集长度比均为3∶1.当风压时程总长取1 000 s时,训练集长度为750 s,测试集长度为250 s;当风压时程总长取1 600 s时,训练集长度为1 200 s,测试集长度为400 s.在进行预测之前,对原始数据进行归一化处理,

图3为本工作中的实测风压预测流程.两种优化算法以及LSSVM的参数设置如下:NPSO=20,TPSO=200,c1=c2=2,ω=1;NCS=20,TPSO=200,pa=0.25;σ∈[10−1,103],γ ∈ [10−1,103].

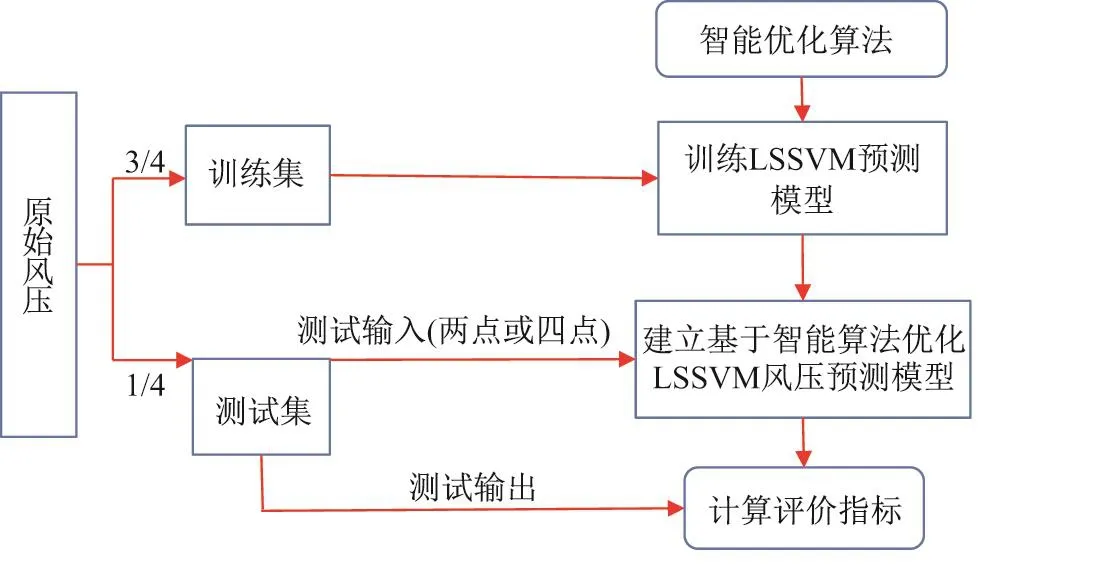
图3 风压预测流程图Fig.3 Flowchart of wind pressures prediction

4.1 内插预测

图4为两种预测模型下不同输入点数内插预测3#测点风压的预测结果与实测风压的比较.从图中可以看出,不管利用PSO-LSSVM还是CS-LSSVM进行内插预测,当输入点数由2变4时的预测结果更接近实测风压.图5为两种预测模型下不同输入点数内插预测3#测点风压的预测结果自相关函数与实测风压自相关函数的比较.从图中可以看出,不管利用PSO-LSSVM还是CS-LSSVM进行内插预测,4点输入的内插预测结果自相关函数比2点输入更加逼近实测风压的自相关函数.

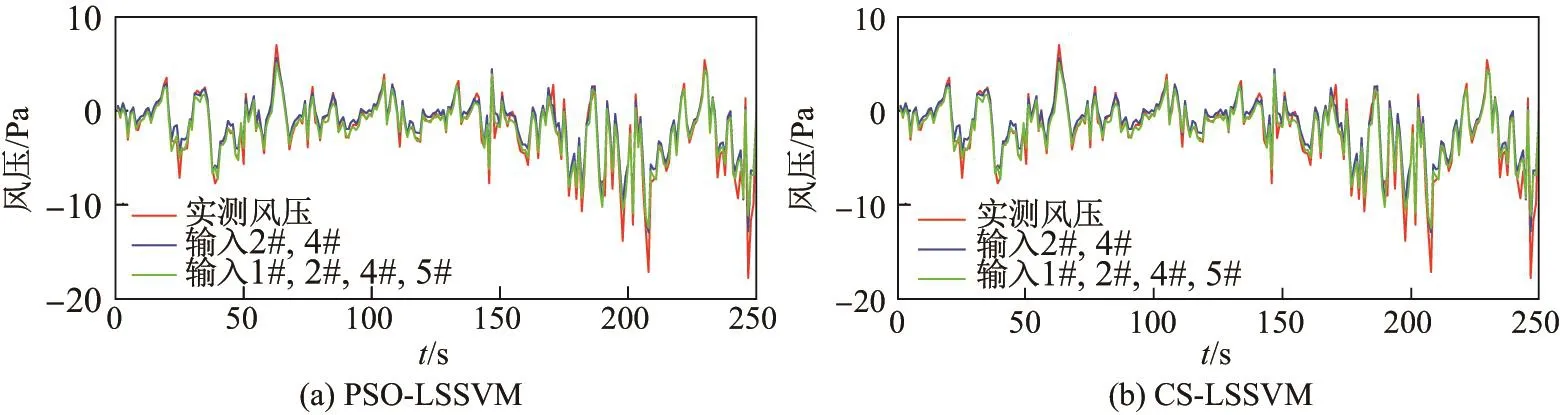
图4 内插预测风压与实测风压的比较(内插预测250 s)Fig.4 Comparison of interpolated predicted wind pressure and measured wind pressure(250 s)

图5 内插预测风压自相关函数与实测风压自相关函数的比较(内插预测250 s)Fig.5 Comparison of autocorrelation function between interpolated predicted wind pressure and measured wind pressure(250 s)

表1为两种预测模型在不同输入点数时内插预测3#测点风压的预测性能指标的对比,其中平均误差均方根误差相关系数R=相对百分误差绝对值的平均值均方根相对误差为目标值(原始样本数据)为预测值,N为预测样本数.由表1可知:①PSO-LSSVM与CS-LSSVM的内插预测性能相当;②不管采用PSO-LSSVM还是CS-LSSVM进行内插预测,当输入点数由2变4时,5项预测性能指标都变得更优,说明增加输入点可提高内插预测性能.

表1 5项预测性能指标对比(1 000 s)Table 1 Comparison of the parameters by the five prediction algorithms(1 000 s)

4.1.2 1 600 s风压时程(内插预测400 s)

图6为两种预测模型下不同输入点数内插预测3#测点风压的预测结果与实测风压的比较.从图中可以看出,不管利用PSO-LSSVM还是CS-LSSVM进行内插预测,当输入点数由2变4时的预测结果接近实测风压的程度没有得到明显提升.图7为两种预测模型下不同输入点数内插预测3#测点风压的预测结果自相关函数与实测风压自相关函数的比较.从图中可以看出,不管利用PSO-LSSVM还是CS-LSSVM进行内插预测,4点输入的内插预测结果自相关函数接近实测风压自相关函数的程度与2点输入的相当.

表2为两种预测模型在不同输入点数时,内插预测3#测点风压的预测性能指标的对比.由表2可知:①此时PSO-LSSVM与CS-LSSVM的内插预测性能相当,但总体而言,CS-LSSVM内插预测性能略优;②不管采用PSO-LSSVM还是CS-LSSVM,当输入点数由2变4时,5项预测性能指标都变得更优,说明增加输入点数可提高内插预测性能.

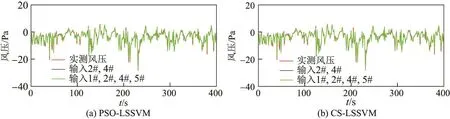
图6 内插预测风压与实测风压的比较(400 s)Fig.6 Comparison of interpolated predicted wind pressure and measured wind pressure(内插预测400 s)

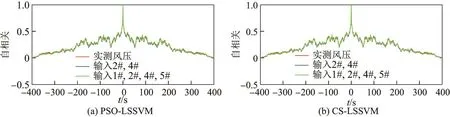
图7 内插预测风压自相关函数与实测风压自相关函数的比较(400 s)Fig.7 Comparison of autocorrelation function between interpolated predicted wind pressure and measured wind pressure(400 s)

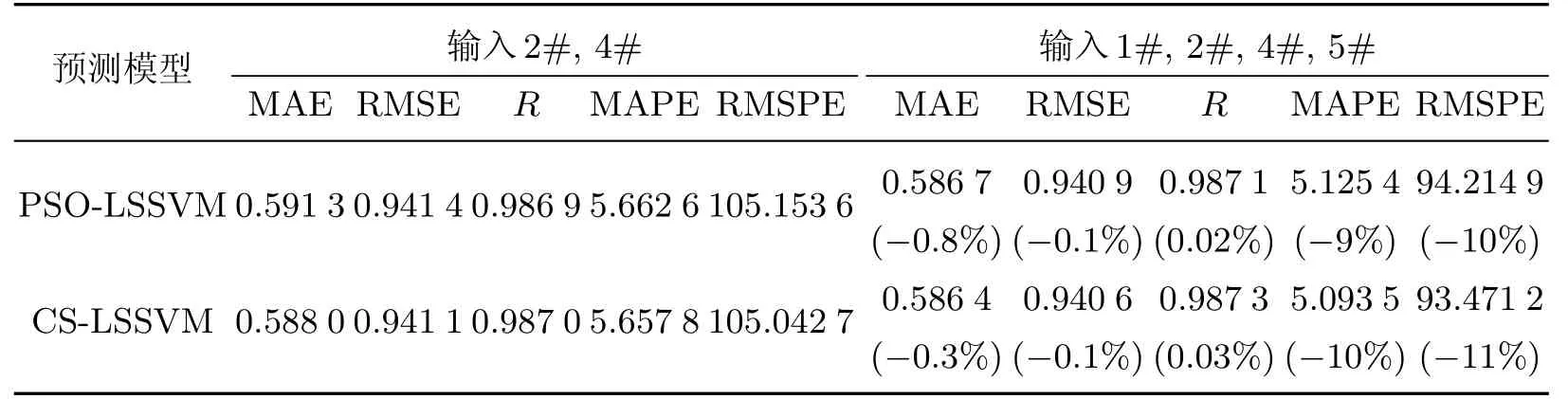
表2 内插预测性能指标的对比(1 600 s)Table 2 Comparison of the parameters by the five prediction algorithms(1 600 s)

对比分析表1和表2可以发现,增加输入点数对原始风压总时长为1 600 s、内插预测400 s内插预测性能的提升程度远低于原始风压总时长为1 000 s、内插预测250 s时的结果.原因是当增加训练集长度时,包含了通过增加输入点可提供给预测模型的大部分信息,故此时增加输入点数可提供给预测模型新的信息已经很少,内插预测性能提升的程度减弱.

4.2 外插预测

4.2.1 1 000 s风压时程(外插预测250 s)

图8∼9分别为两种预测模型下不同输入点数时外插预测1#测点风压的预测结果与实测风压的时程、自相关函数的比较.从图中可以看出,不管是PSO-LSSVM还是CS-LSSVM进行外插预测,当增加输入点数时,预测结果接近实测风压的程度和预测结果自相关函数接近实测风压自相关函数的程度都略有提升,但是提升程度很小.

表3为两种预测模型在不同输入点数时外插预测1#测点风压的预测性能指标的对比.由表3可知:①PSO-LSSVM与CS-LSSVM的外插预测性能相当;②不管采用PSO-LSSVM还是CS-LSSVM进行外插预测,当输入点数由2变4时,5项性能指标都变得更优,说明增加输入点数可提高外插预测性能,但此时提升的程度远低于原始风压总时长为1 000 s内插预测250 s的情况,因此增加输入点数对内插预测性能的提升效果优于外插预测.

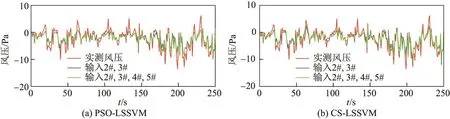
图8 外插预测风压与实测风压的比较(250 s)Fig.8 Comparison of extrapolation predicted wind pressure and measured wind pressure(250 s)

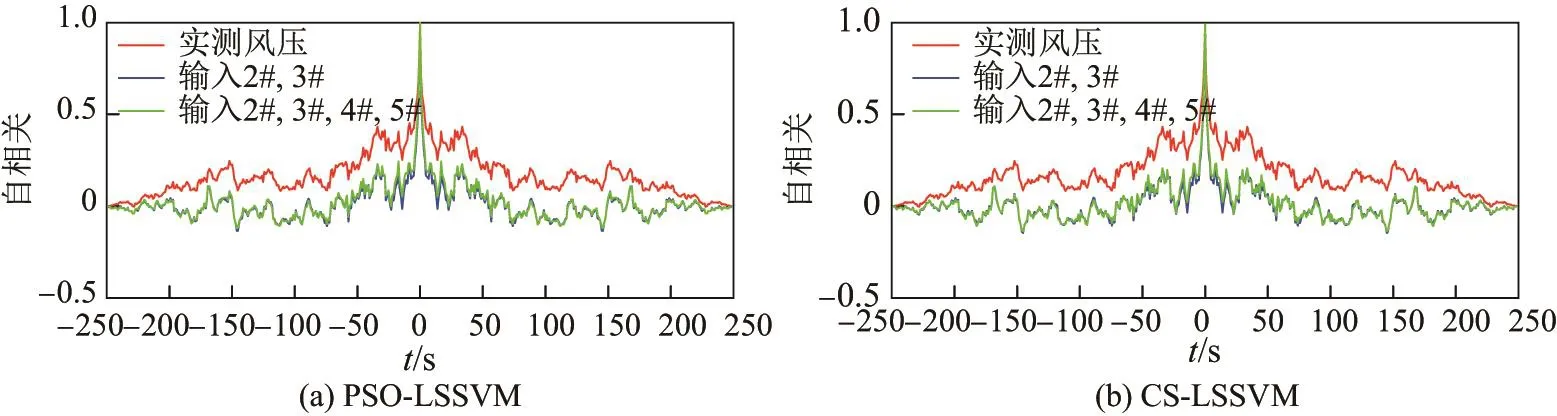
图9 外插预测风压自相关函数与实测风压自相关函数的比较(250 s)Fig.9 Comparison of autocorrelation function between extrapolation predicted wind pressure and measured wind pressure(250 s)

4.2.2 1 600 s风压时程(外插预测400 s)

图10∼11为两种预测模型下不同输入点数时外插预测1#测点的预测结果与实测风压的时程比较、自相关函数的比较.从图中可以看出,此时不管是PSO-LSSVM还是CS-LSSVM进行外插预测,当增加输入点数时,预测结果接近实测风压的程度和预测结果自相关函数接近实测风压自相关函数的程度都基本不提升.

表3 外插预测5项性能指标的对比(1 000 s)Table 3 Comparison of the parameters by the five prediction algorithms(1 000 s)

表4为两种预测模型在不同输入点个数时,外插预测1#测点风压的预测性能指标的对比.从表中可以得知:①PSO-LSSVM与CS-LSSVM的外插预测效果相当;②不管采用PSOLSSVM还是CS-LSSVM进行外插预测,当输入点数由2变4时5项预测性能指标都变得更优,说明增加输入点数可提高外插预测性能,但此时提升的程度低于原始风压总时长为1 000 s外插预测250 s的情况,原因是当增加训练集长度时,包含了通过增加输入点可提供给预测模型的大部分信息,故此时增加输入点数可提供给预测模型新的信息已经很少,外插预测性能提升的程度减弱.比较表4和表2可知,在原始风压总时长为1 600 s、预测400 s情况下,当输入点数由2变4时,外插预测在MAE,RMSE,R三项指标的提升程度优于内插,而在MAPE,RMSPE两项指标的提升程度低于内插,此时可认为增加输入点数对内插预测的提升与外插预测的提升效果相当.原因是当增加训练集长度时,可提供足够的信息给预测模型,弥补了外插预测的先天不足.

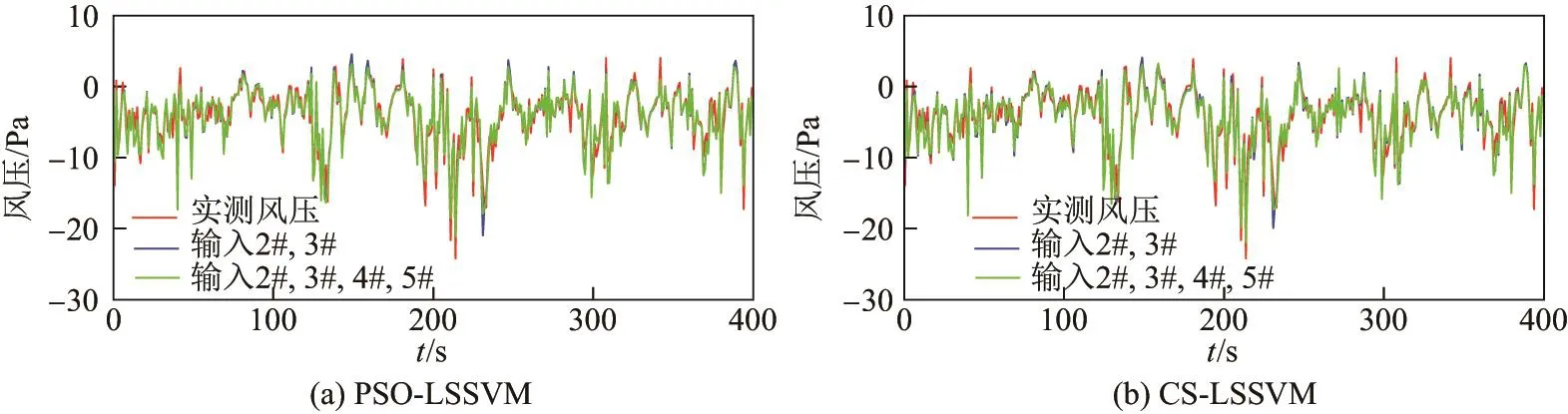
图10 外插预测风压与实测风压的比较图(400 s)Fig.10 Comparison of extrapolation predicted wind pressure and measured wind pressure(400 s)

图11 外插预测风压自相关函数与实测风压自相关函数的比较(400 s)Fig.11 Comparison of autocorrelation function between extrapolation predicted wind pressure and measured wind pressure(400 s)

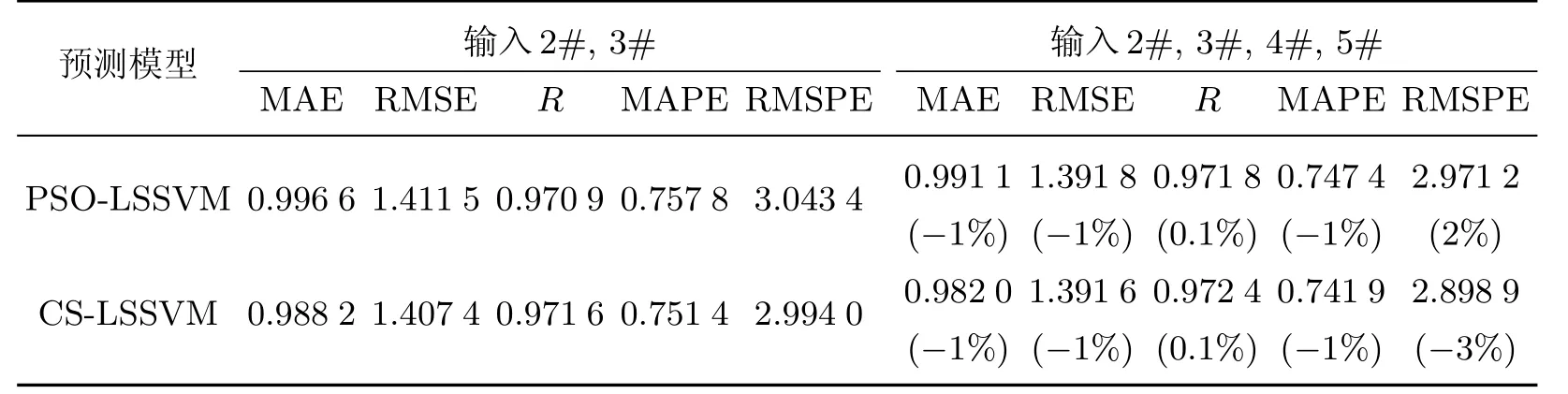
表4 外插预测5项性能指标对比(1 600 s)Table 4 Comparison of the parameters by the five prediction algorithms(1 600 s)

5 结束语

本工作通过增加输入点数来提升最小二乘支持向量机对未知风压点风压的预测性能,并分别进行内插预测与外插预测,其中LSSVM的参数组合(γ,σ)寻优采用PSO以及CS算法.研究结果发现:①PSO-LSSVM的预测性能和CS-LSSVM相当,增加输入点数在这两种LSSVM中表现出相同的规律;②当输入点数增加时,不论内插预测还是外插预测,5项预测性能指标都得到提升,但是当增加训练集长度时,提升效果减弱;③当增加输入点数时,内插预测的5项预测指标提升程度远大于外插预测,但是当增加训练集长度时,内插预测5项指标的提升程度与外插预测相当.

致谢:本工作中部分数据由华东交通大学的李锦华博士提供,在此表示由衷感谢!