基于需求学习的可替代服装产品动态库存与定价联合决策模型

高峻峻,袁君霞

(1.上海大学悉尼工商学院,上海201800;2.上海大学管理学院,上海200444)

流行品(fashion or style goods)中的典型产品——服装是一种短生命周期产品,与同属短生命周期产品中的易腐品或易变质品的主要区别在于:后者因变质、过期、挥发等物理价值损失造成产品使用价值逐渐下降,而前者是由于消费者需求变化而引起产品使用价值下降.服装之间的替代性非常强,易受到价格、流行元素、季节性、消费者偏好、营销方式等多种因素影响,销售季节常常仅为2∼3个月.服装固有的高需求不确定性、短生命周期性等使得服装供应链很难实现供需的完美匹配,无论是供应商、原始设备制造商(original equipment manufacture,OEM)生产商还是品牌商,都不愿意承担高需求不确定性所带来的库存风险,于是,高库存、补货难成为了诸多服装企业运营中难以规避的“瓶颈”环节.帮助服装企业找到构筑自身竞争优势的合适的需求管理策略和库存管理策略、定价策略已成为迫切需要解决的问题.

对于服装产品的研究始于20世纪50年代,当时服装产品的特点就引起了部分学者的关注.Whitin[1]的研究表明,假设服装产品在不同定价水平上的平均需求的概率分布是己知的,当销售价格为常量时的订货量就是标准的经济批量(economic order quantity,EOQ).Muarry等[2]同时考虑潜在客户的数量和潜在客户选择某一产品的概率,给出了服装产品库存问题的动态规划公式,这一思路至今仍为多数动态定价研究所采用.在需求学习领域,Dvoretzky等[3]最早使用贝叶斯模型来讨论需求更新的动态特性,Scarf[4]则最早将贝叶斯方法应用到库存理论中研究了简单的周期库存问题.20世纪80年代末,服装产品作为一种具有高额利润空间的产品,日益为实业界所重视,进而得到了学术界的关注.很多学者在Scarf研究的基础上从需求分布的描述角度对库存模型进行了扩展,例如:假定顾客每期的到达率未知,但服从泊松分布;未知需求率的先验分布假定为Gramma分布;需求是具有gamma先验均值的指数分布[5];假定需求服从负二项分布[6];每个时期的需求都为关于价格的确定地、同分布函数,且参数未知[7]等.

综上可以看出,以往针对服装产品的研究往往集中于:①考虑价格敏感性需求下基于需求分布参数更新的动态定价问题研究[8-10],此类研究往往以单一产品为研究对象[11];②考虑需求学习或需求预测更新的服装品动态库存模型研究[12-16];③将以上两个方面进行整合研究,考虑需求学习的定价与库存联合决策模型[17-18].尽管需求学习和需求预测更新方法在服装行业的应用前景已经得到诸多学者的认可,如快速响应和协同式供应链库存管理(collaborative planning forecasting and replenishment,CPFR)策略在服装业的推广,而且这一研究方向却被认为是今后50年运营管理发展的主要趋势[19-21],但由于建模的复杂性,同时将需求学习、需求替代性、动态库存和动态定价集成化决策的研究还是相对较少,至今只看到一篇文献同时考虑了需求学习和替代率学习,并在此基础上对动态库存管理问题进行的研究[22].但是,此文献的研究对象为单一非短生命周期产品.

本工作建立的模型解决的是更为一般的问题,主要体现在:①选用款式多样的服装产品为研究对象开展多产品研究;②将需求替代性和需求学习同时引进服装供应链模型,针对由一个服装零售商和一个服装制造商组成的供应链,研究了该短生命周期产品供应链中需求学习与需求替代性对动态库存管理与动态定价的影响.这一研究对于解决服装业的库存问题具有很强的现实意义.实际上,消费者在购买产品、尤其是服装产品时,面临的往往是两种或两种以上的产品选择,比如一个服装零售终端同一品类下会有十几种甚至几十种款式供消费者选择,所以对多产品开展研究具有更现实的实际意义;其次,同时考虑需求学习、需求替代的动态库存定价联合决策模型能够更好的指导企业备货与定价,随着网络经济时代或消费者经济时代的到来,消费者想要购买的产品如果无法即时获得,他们往往选择去其他店铺购买,除非有满意的可替代产品,所以基于需求学习与需求替代的动态定价与库存管理模型能够更好地优化库存管理,降低库存成本的同时,提高消费者满意度和企业利润.

综上,首先假定服装产品分两批上市,两批次产品为同一大类下具有替代性的产品,按照产品分批上市的时间节点,将销售季节划分为两个阶段,在考虑产品间缺货替代率的基础上构建需求学习模型,即零售商在销售季节初发出初始订单,在销售季节第一阶段结束时对订单按照实现需求进行更新;然后,以需求学习模型为输入,建立基于需求学习的流行服装供应链的动态库存与定价的联合决策模型,零售商通过该模型找到各个时间段针对不同产品的最佳订货量和库存控制策略,制造商通过该模型确定各个产品在各个时间段的最佳批发价格;最后,给出算例的计算结果和仿真分析结果以说明模型的有效性和应用效果.研究结果表明:需求学习可以给服装供应链带来显著的利润提升,企业通过同时将需求学习和需求替代性合并至库存与动态定价联合决策模型可以实现最好的绩效,但当企业不具备同时实施需求学习和需求替代性估计两方面工作的时候,单纯实施需求学习也可以取得较好的效果;如果供应链信息化程度或管理水平很难实现需求学习时,将需求替代性考虑到库存模型中就显得非常重要,此时单纯考虑需求替代性也会带来利润的显著提升;模型的仿真结果表明,该模型非常适用于当前服装企业所处的顾客忠诚度持续下降的商业环境.

1 问题描述与符号

针对由一个零售商和一个制造商组成的“一对一”服装供应链,制造商的服装产品为分批上市,两批次产品为同一大类下具有替代性的产品(产品i=1,2);按照产品分批上市的时间节点,将销售季划分为两个阶段(阶段t=1,2,分别表示销售季节的第1阶段和第2阶段),如图1所示.假定产品1在销售季节的第1阶段上市,产品2在销售阶段的第2阶段上市,两种产品之间具有替代性,产品1在销售季节的不同时期的需求具有相关性.零售商在销售季节前对产品1进行一次订货,在销售季节的第1阶段和第2阶段交替的节点可进行补货和调价,并根据产品1在销售季第1阶段的实际销售数据对第2阶段的产品1和产品2的需求进行学习.

通过对某时尚快销品牌的销售数据进行跟踪,我们发现服装产品从需求的连续性和平稳性方面可以分为两类:①经典款和主推款;②时尚款和形象款.经典款和主推款的需求量往往较大且连续,没有大起大落的销量,促销时的价格敏感性较强.针对这一类产品,我们认为其较符合需求描述中的价格敏感性和正态分布特性.因此,本工作假定这两个产品属于经典款和主推款类别,需求具有价格特性且服从正态分布,可以根据同类产品的历史数据估计其均值和方差.假设两产品的缺货替代率与客户忠诚度相关,由于两种产品隶属于同一品牌,故顾客忠诚度差别不大.假设已经实现的需求Di,t与下一阶段需求Di,t+1服从二维正态分布,其中Di,t表示顾客对产品i的第t阶段的需求,服从正态分布,用fit(x)表示其概率密度函数.模型中的参数Hi为零售门店关于产品i的单位库存持有成本占单位批发价格的百分比,Vi为零售门店关于产品i的单位返还价格占单位批发价格的百分比,bi为制造商关于产品i的季末单位残值占单位批发价格的百分比,Ci为制造商关于产品i的单位生产成本,Yi为制造商关于产品i的单位运输成本,di为产品i的客户忠诚度.决策变量Qit(kit)为零售门店对产品i在第t阶段向制造商发出的订货量,为安全库存因子kit的函数,Pit为零售门店对产品i在第t阶段制定的单位销售价格,wit为制造商对产品i在第t阶段制定的单位批发价格.

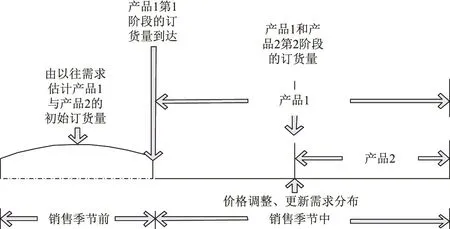
图1 产品分批上市示意图Fig.1 Sketch map of product listing in batches

2 贝叶斯需求学习

贝叶斯学习的推导过程[23-25]现以引理形式列出.假设需求不确定性来自:①需求产生过程中,零售商根据已有的历史销售资料,预测到即将面临的需求D,由于需求是随机的,可将其用随机变量刻画,假定需求服从均值为θ,方差为σ2的正态分布;②对需求本身的参数θ估计的不确定性,在上一销售期的观察数据引入后θ会发生变化,故设其服从均值为u,方差为τ2的正态分布.

引理1若则零售门店在销售初期预测整个销售季节的需求为

引理2若经过第1期的销售,零售门店获得了新的销售信息D0,在D0已知的条件下更新需求均值可得

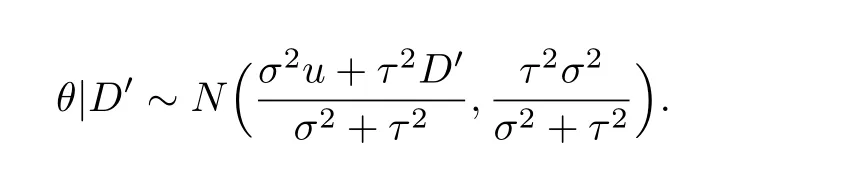
引理3将引理2得出的需求均值θ|D0带入引理1,即将整个销售季节的需求均值更新后可以得到更新后的需求分布

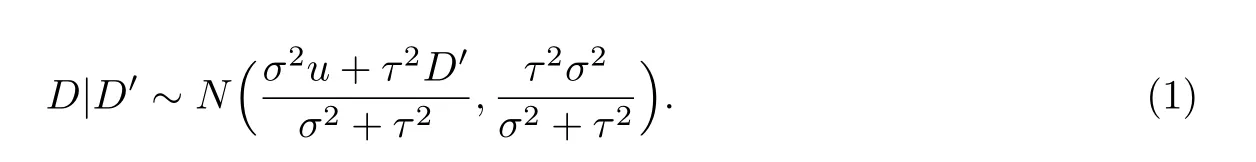
引理4已知两批上市产品相关并服从二维正态分布,即服从二维正态分布,相关系数为ρ,故得到产品1的销售数据后,即在已知需求的条件下,可以更新产品2的需求分布为且服从正态分布

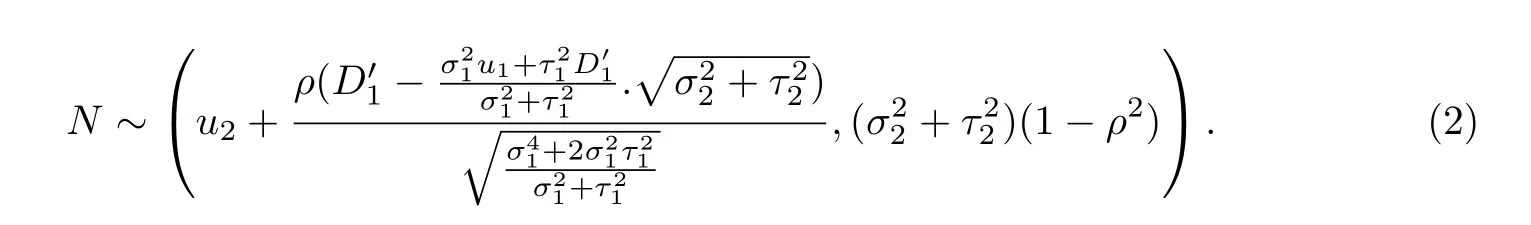
引理5已知D∼N(u,σ2),Q,EI,ES,EQ分别代表订货量、期望库存水平、期望缺货量和期望销售量,则连续检查库存策略下,有

3 模型

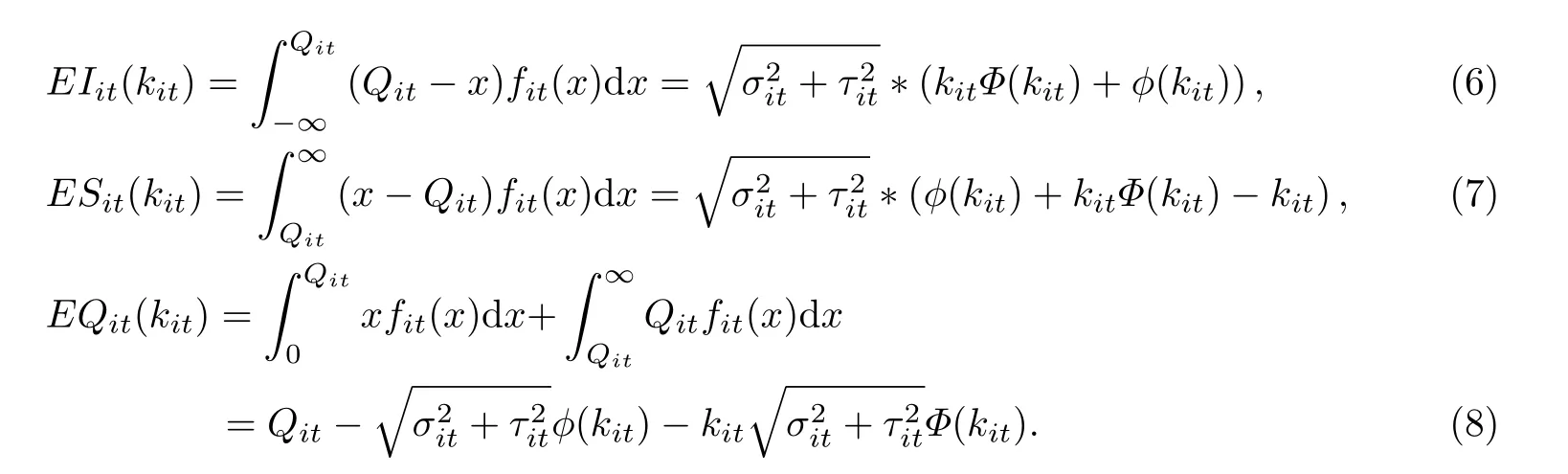
假设两种产品之间的替代类型为基于缺货的替代,在考虑代替性的情景之下,用产品i第t阶段的有效预期库存水平、有效预期缺货量和有效预期销售量来表示有效需求下的预期库存水平、预期缺货量和预期需求量,其中产品1在第一阶段的预期库存水平、预期缺货量和预期需求量不发生变化,即但产品1在第二阶段和产品2在第二阶段上市后因为需求均值发生变化而带来预期库存水平、预期缺货量和预期需求量都将发生变化,其均值变为

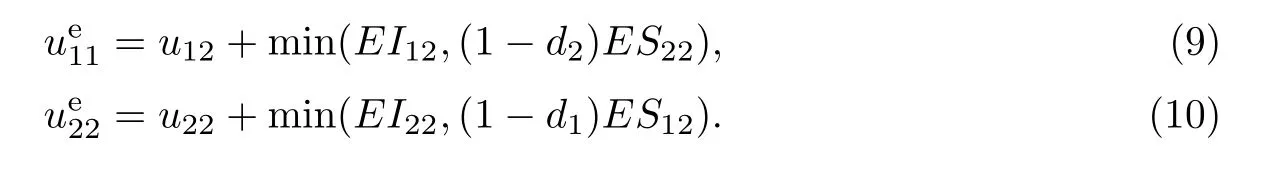
产品1在第二阶段和产品2在第二阶段上市后的需求方差不变,进而可求得

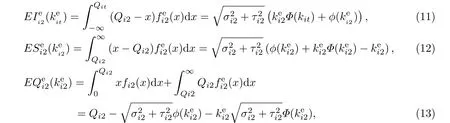
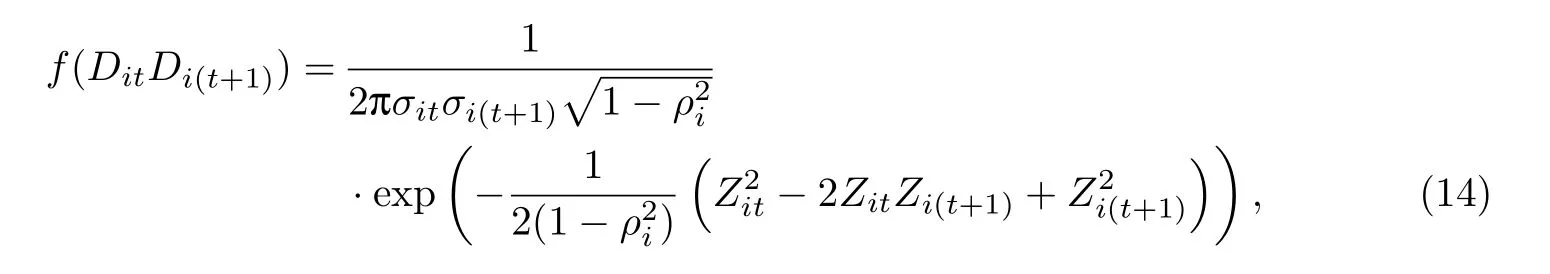
综上,可利用已经实现需求信息D011,依据引理3和引理4更新未来需求分布的参数,具体见表1.

表1 需求学习后的各阶段需求分布的均值和方差Table 1 Mean and variance of demand distribution in each stage after demand learning

服装供应链在整个销售季节的预期总利润(π)包括零售门店的期望利润(πR)和制造商的期望利润(πM),其中零售门店期望利润包括产品的期望销售收入(Rrr)加上期望返还收入(Rrb),同时减去发生的采购成本(Crp)和期望库存持有成本(Crh).制造商期望利润包括批发收入(Rmw)加上残值收入(Rms)减去生产成本(Cmp)、运输成本(Cmt)和返还支出(Cmb).

于是有

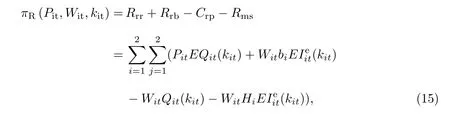
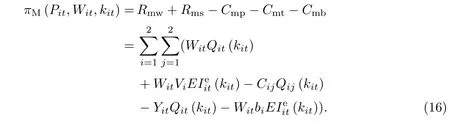
为寻求服装供应链利润最大,建立如下库存/定价联合决策模型:

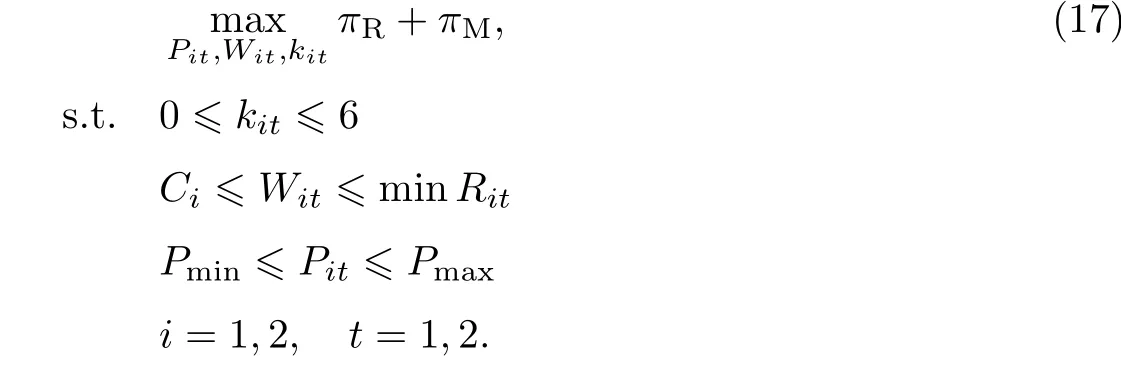
模型(17)可采用数据嵌套循环方法进行求解,即令安全因子kij在闭区间[0,6]内变化,零售门店的销售价在[Pmin,Pmax]内变化,制造商可接受的批发价格在成本价与最小销售价格范围内变化时,搜索系统利润最大时的安全库存因子、零售价格和批发价格.如果零售店和制造商的利润函数中的预期库存水平、预期缺货量和预期销售量中不考虑需求替代,则采用式(6)∼(8)计算出的原始预期库存水平、预期缺货量和预期销售量替换下有效预期库存水平、预期缺货量和预期销售量,即可得到未考虑需求替代的供应链利润.如果在计算预期库存水平、预期缺货量和预期销售量过程中用到的需求分布的参数(均值和方差)采用初始参数值则为未考虑需求学习的供应链利润,采用表1中更新后的参数值则为考虑需求学习的供应链利润.因此,通过模型(17)可以得到4类供应链利润:①有需求替代但无需求学习下的供应链利润(DS-only);②是无需求替代无需求学习下的供应链利润(N-DSDL);③是无需求替代但有需求学习下的供应链利润(DL-only);④是有需求替代和需求学习下的供应链利润(DSDL).

4 算例及仿真分析

以某品牌服装制造商向一零售门店供应一类产品的服装供应链为例,进行仿真分析.假定该品牌供应商销售两款款式不同的产品,分别为产品1(长款男士上衣),产品2(短款男士上衣),因为男士上衣较女装的需求更为平稳,故符合本模型中需求服从正态分布的假设.产品分两批上市,总的销售时间为15周.产品1在期初进入市场,产品2在销售期2初(销售期1末)才进入市场,与产品1一起销售,此时,产品1进行一次调价.表2列出了模型中用到的参数值.

表2 模型中的主要参数值Table 2 Main parameter values in the model

将表2中参数带入DS-only情景下的模型和DSDL情景下的模型,对于考虑需求学习前后的供应链利润和最优解进行比较,结果见表3.

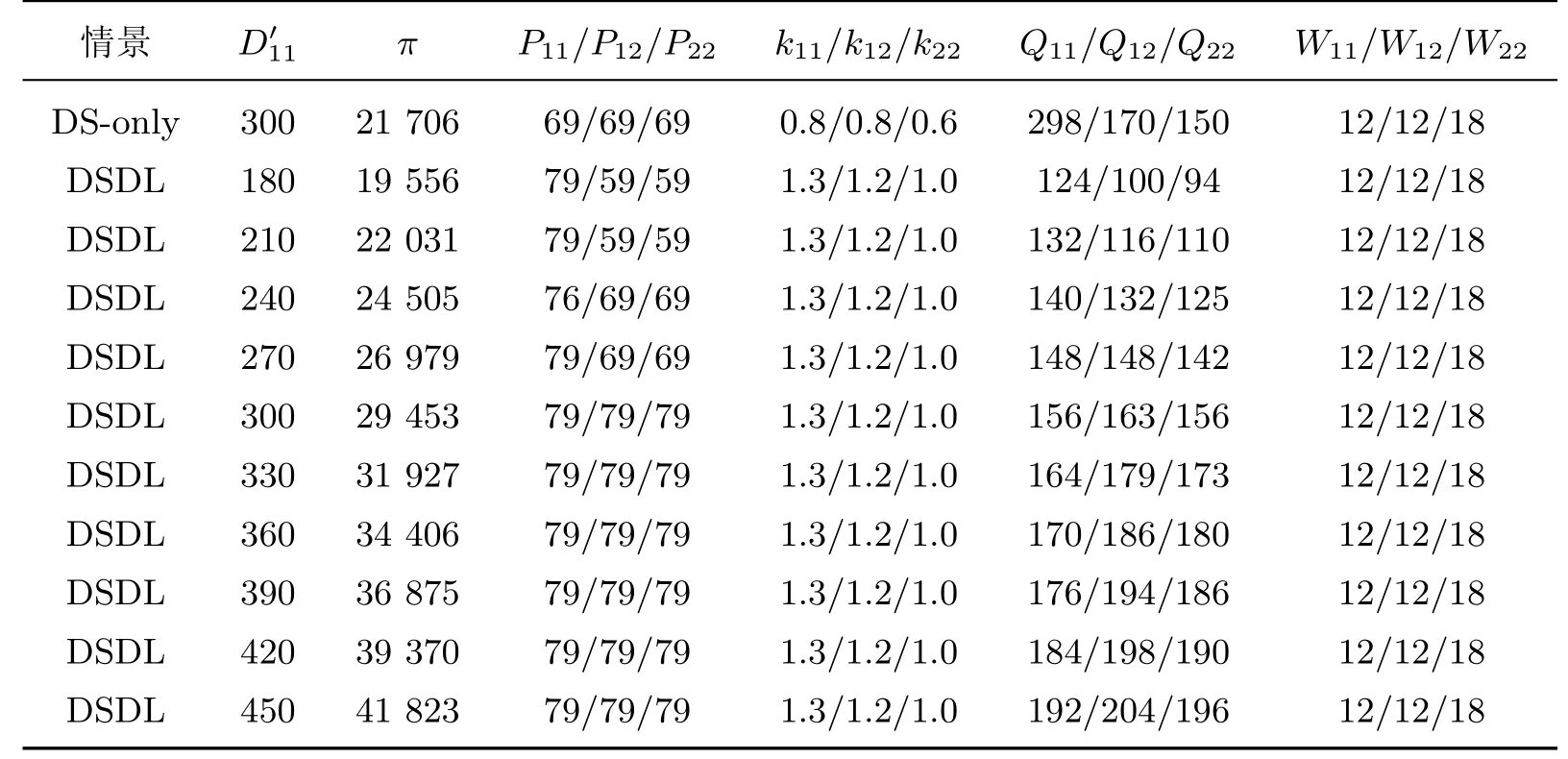
表3 服装供应链最优利润及模型最优解Table 3 Optimal profit and optimal solution of apparel supply chain

从表3可以看出,DS-only情景下的供应链最大利润为21 706,DSDL情景下的最优利润达到了29 453,说明了需求更新将使得供应链的利润值增长35.7%.此外,从考虑需求学习情景下的最优动态价格可以看出:随着第一期实现需求信息的获取,当销售季节第一期实现的需求量较小(180∼210)时,产品1和产品2在销售季节第二期的最优定价相比初始定价69元都要低一些,低至59元;当销售季节第一期实现的需求量接近估计值300时,产品1和产品2在销售季节第二期的最优定价与初始定价相同;但当销售季节第一期实现的需求量大于等于300时,产品1和产品2在销售季节第二期的最优定价相比初始定价69元都要高一些,高至79元.从需求学习情境下的供应链利润可以看出,供应链利润与需求学习具有正相关性.

图2为4种情境下的供应链利润的变化.从图2可以看出:当没有考虑需求学习的时候,DS-only情景下和N-DSDL(d1变化,d2变化)情景下的供应链利润与产品1在第一阶段已实现的需求无关,为一条水平的直线,但DS-only情景下的供应链利润显著好于N-DSDL情景;当考虑需求学习的时候,无论是否考虑需求替代,供应链利润都与已实现需求正相关,即随着已实现需求的上升;DSDL情景下的供应链利润高于DL-only情景下的供应链利润.

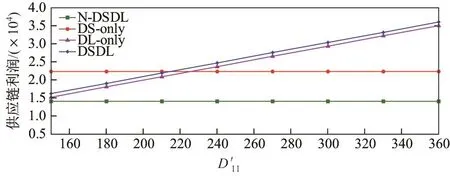
图2 4类情景下供应链利润对比Fig.2 Comparison of supply chain profit under four kinds of scenarios

由于客户忠诚度会影响产品间的缺货替代率,因此需要进一步分析DSDL情境下客户忠诚度di对供应链利润的影响,结果如图3所示.从图3可以看出,供应链利润与客户忠诚度d1,d2均为负相关关系,即客户忠诚度越低,供应链利润越高.

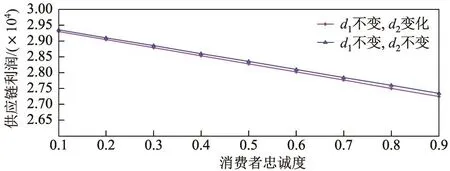
图3 消费者忠诚度对供应链利润的敏感性分析Fig.3 Sensitivity analysis of consumer loyalty to supply chain profit

最后,对需求不确定性程度进行敏感性分析,其中考虑了随着需求方差的组成中σij,τij的变动.DS-only情境下和DSDL情境下供应链利润的变动程度,结果如图4所示.

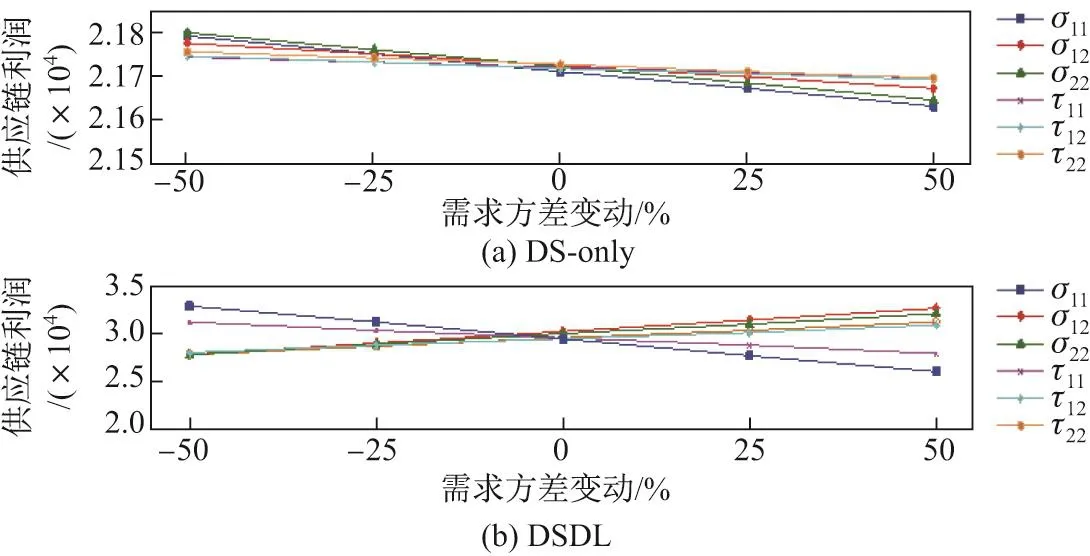
图4 需求方差变动的敏感性分析Fig.4 Sensitivity analysis of change of demand variance

从图4可以看出,仅考虑需求替代性不考虑需求学习的DSt-only情境,供应链利润随着需求方差的增加而下降;而需求替代性和需求学习均考虑的DSDL情景,产品2的供应链利润与需求方差的变动没有明显的相关性,需求方差正向变动时供应链利润不降反升,显示了需求学习的鲁棒性和优越性.可见,需求学习利用前期信息可以有效减少未来需求不确定性,增加未来预期供应链利润.因此,如何进行合理分配该部分利润,协调制造商和零售门店以及如何构建更一般的分布函数,改进更新后的预测准确度是下一步的研究方向.

5 结束语

本工作在考虑产品间缺货替代率的基础上,针对由一个服装零售商和一个服装制造商组成的服装供应链,建立了基于需求学习的动态库存与定价的联合决策模型,研究了需求学习与需求替代性对动态库存管理与动态定价的影响.实验表明,在当前服装企业所处的顾客忠诚度持续下降的商业环境中,无论是否考虑需求替代,需求学习都可以给服装供应链带来显著的利润提升,但同时考虑需求学习和需求替代性时,可以实现最佳的供应链绩效;如果供应链信息化程度或管理水平很难实现需求学习,将需求替代性考虑到库存模型中就显得非常重要,单纯考虑需求替代性也会取得较好的效果.

本工作考虑需求替代性的情况下,以实现利润最大化为目标,研究了流行服装行业单一销售季节下包含两个产品的基于需求学习的动态库存与定价联合决策问题.但很多情况一个服装供应链是由多个零售商和一个制造商组成,或多个零售商和多个制造商组成,而且每一个服装零售终端同一品类下会有十几种甚至几十种款式供消费者选择,不同的零售店铺之间也会对紧急订单进行调拨,此时问题会更加复杂,但也更接近于服装供应链的实际情况.因此,下一步的重点研究方法为考虑一个销售季节多个产品且有需求替代性情境下基于需求学习的流行品供应链的动态库存、定价与紧急订单(调拨)的联合决策模型.