不同模量铁木辛柯梁的自由振动特性分析

杨 洋,姚文娟

(上海大学土木工程系,上海200444)

土木工程中的振动问题是较为常见的力学现象.振动过程中结构的形状、承载力会在极短的时间内发生急剧的变化,对其工作性能和使用寿命会产生严重的影响.梁是实际工程中常见的一种构件,其变形在荷载作用下大多是小变形,且不管荷载是纵向或者横向,都可使梁产生振动.大量试验和研究表明,许多材料都具有拉压弹性模量不同的性质.工程中广泛应用的材料如混凝土、金属合金、生物材料[1]、橡胶、岩石等,特别是近年发展起来的新型聚合材料和复合材料都具有明显的这一特征,其拉压模量之比高达4倍[2],且该性质对结构的力学行为有较大的影响.但是,在工程设计中,一般对材料的不同拉压弹性模量不予考虑,但在某些情况下会因本构关系不符合造成较大误差,存在安全隐患.

国内外的众多学者对拉压不同模量材料的结构进行了大量研究.杨海天等[3]研究了不同模量材料的本构关系.姚文娟等[4-8]对复杂应力状况下不同模量弹性结构的解析解进行了研究,给出了不同模量横力弯曲梁、弯压柱、超静定结构、组合结构、不同模量结构温度应力问题内力及变形的解析解.Leal等[9]对不同模量高性能纤维的抗压强度进行了分析.何晓婷等[10-11]用有限元方法对不同模量结构进行收敛性分析,并应用Kirchhoff假设对不同模量的弯曲薄板进行了分析.黄翀等[12]和吴晓等[13-15]采用直线法假定,在分布荷载、热应力作用下不同模量板内力及变形的解析解,结合大挠度理论进行了不同模量板的弯曲分析.上述研究主要针对不同模量结构静力问题,对不同模量结构的振动问题仅有少量学者进行了研究.Iwase等[16]基于数值模拟对不同模量深梁进行了动态响应分析.赵荣国等[17]采用单自由度系统对不同拉压特性结构进行了振动分析.刘相斌等[18]在平截面假定下求解了不同模量弯曲梁的自由振动.王铭慧等[19]研究了微幅自由振动时不同弹性模量材料简支梁的线性振动问题.

以上不同模量结构振动问题的研究是基于数值模拟、单自由度体系及平截面假定等简化条件.鉴于此,本工作基于弹性力学、结构力学及不同模量理论,推导了不同模量材料剪切弹性模量及弯曲刚度的表达式,并建立了考虑剪切效应的不同模量铁木辛柯梁的振动微分方程,得到了不同模量简支铁木辛柯梁在任意分布荷载作用下的自由振动频率解析解.另外,增加梁的跨高比,解析模型可以退化为欧拉-伯努利梁的自由振动频率解析解.

1 基本方程及中性轴位置

均匀简支梁如图1所示.假设均匀简支梁的位移分量为

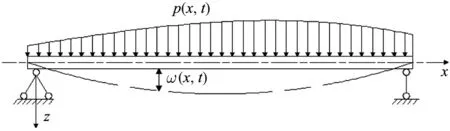
图1 简支梁的弯曲变形Fig.1 Bending deflecting of simply supported beam

由弹性力学理论可知,均匀简支梁的几何方程和物理方程分别为

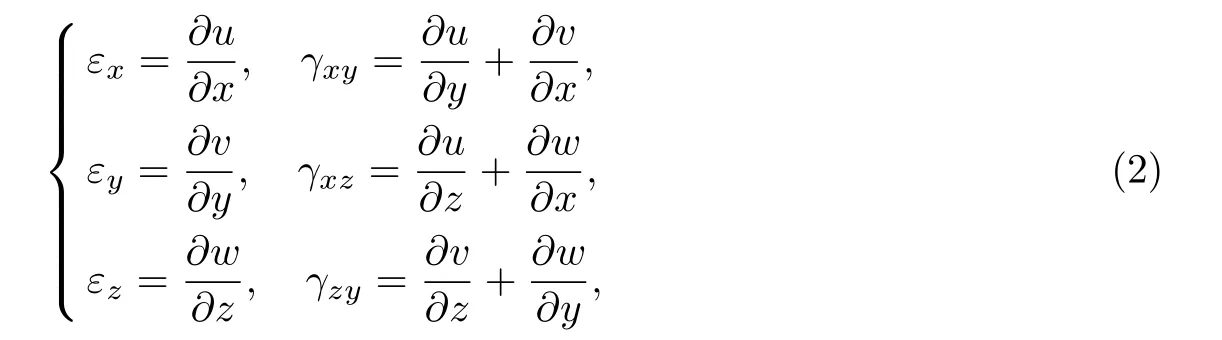
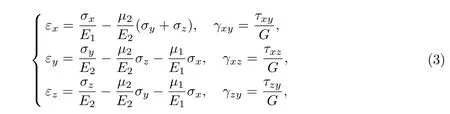
式中:E1,µ1为拉伸时材料的弹性模量和泊松比;E2,µ2为压缩时材料的弹性模量和泊松比.

将式(1)和(2)代入式(3),可得

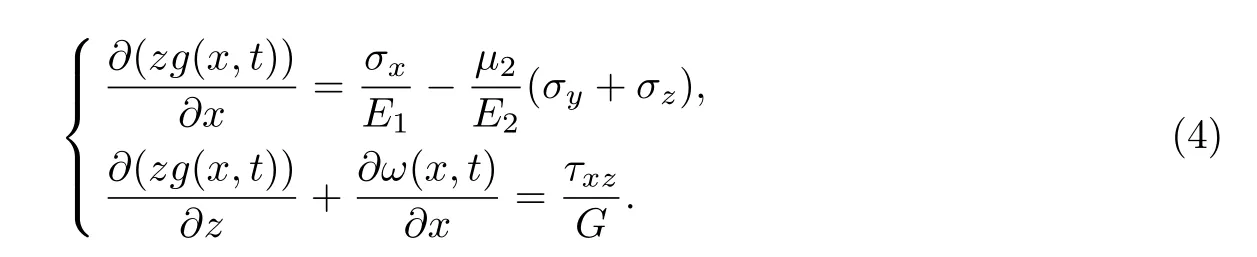
由于土木工程中µ为高阶微量,故可略去,整理得

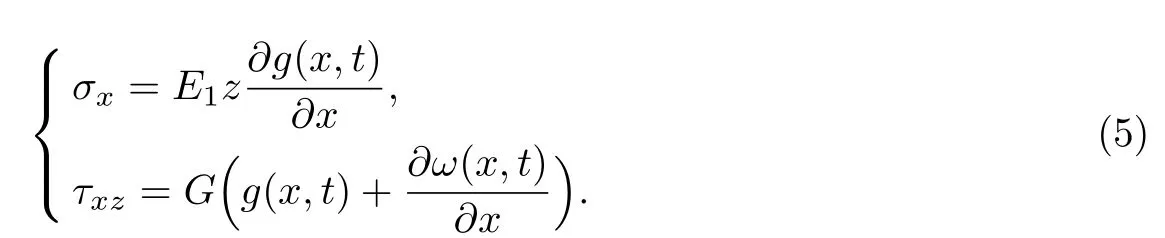
由图1可知,梁在荷载p(x,t)作用下同一截面上有拉有压.由式(5)得到的正应力,为受拉时的正应力公式,而当截面受压时,同理可得受压时的正应力为

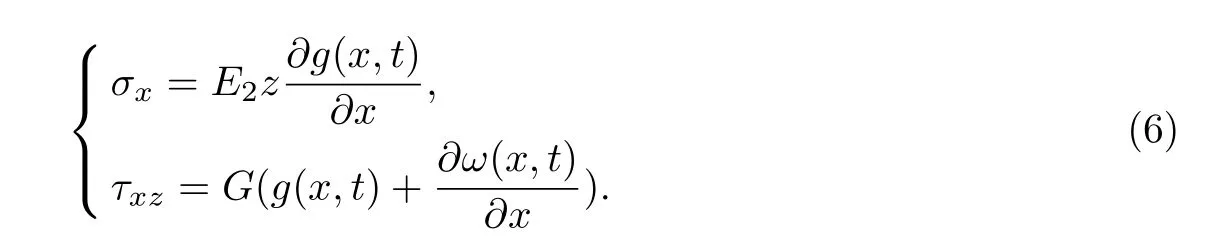
不同模量连续梁在外荷载作用下会形成拉压弹性模量不同的拉伸区和压缩区,因此研究不同模量梁的变形首先需要确定在外荷载作用下的中性层位置,其在受拉和受压区的应力分别为

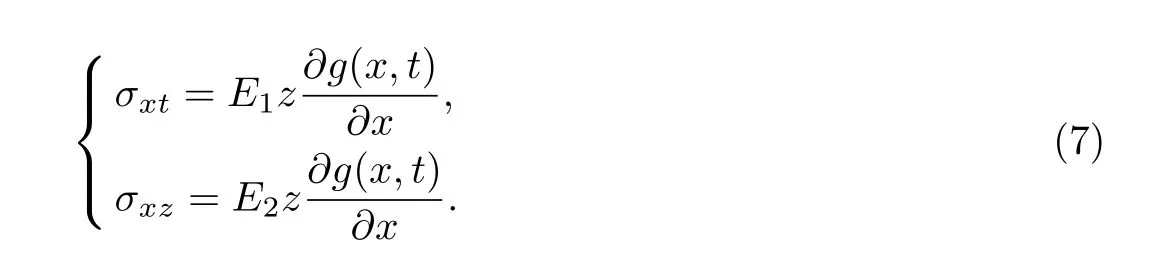
假设梁高为h,截面受拉区高度为h1,受压区高度为h2,取微元体为隔离体,由平衡条件和圣维南原理可得

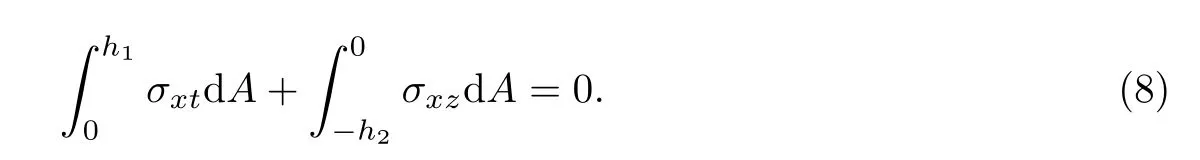
将式(7)代入式(8),可得

以上推导的不同模量梁的中性轴位置与文献[4]的结果一致,由此可知不同横向荷载对不同模量梁的中性轴位置无影响,即剪应力对中性轴的位置无影响.

2 剪切弹性模量及弯曲刚度

不同模量材料的单元体纯受剪示意图,如图2所示.当单元体为纯剪切受力时,应变能密度为

当材料为纯剪受力状态时,由材料力学理论可得

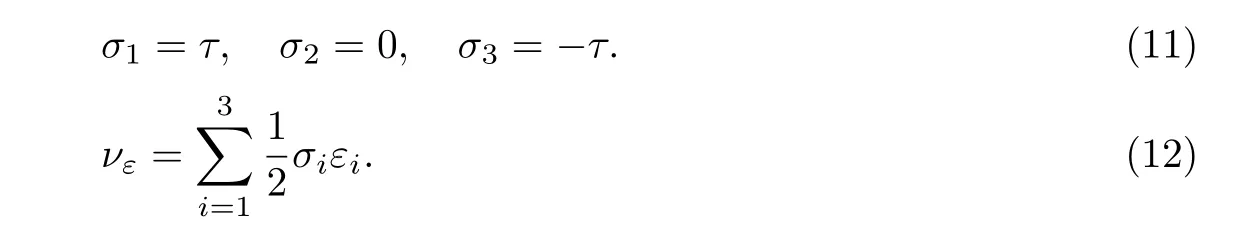
将式(3)和式(11)代入式(12),可得

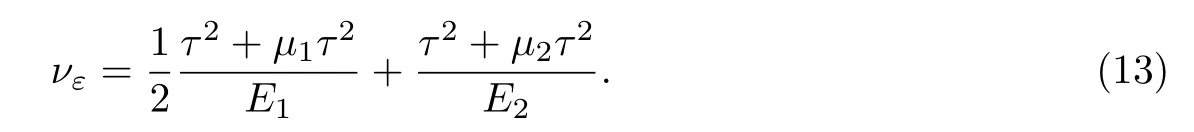
根据式(10)与式(13)相等,故可求得不同模量材料剪切弹性模量

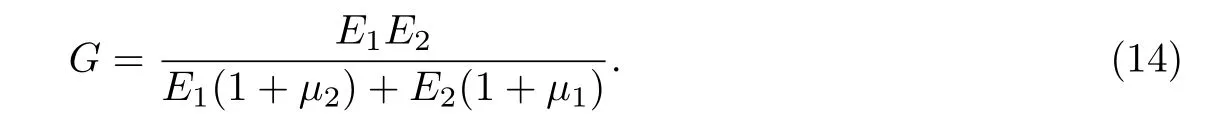
由材料力学理论公式,可得

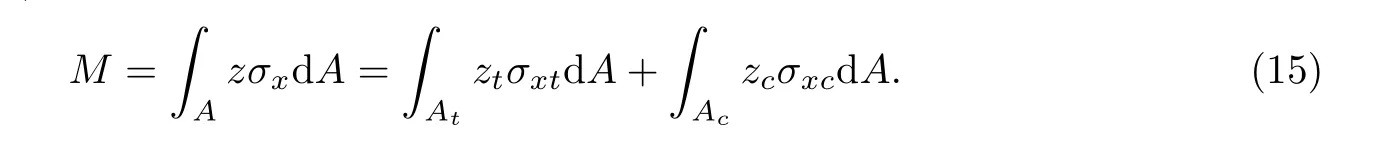
将式(5)和(6)分别代入式(15),可得

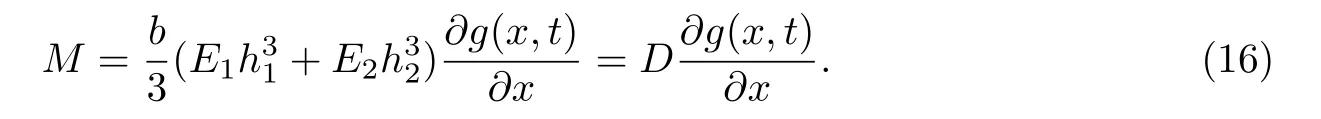
对比式(15)和(16)可求得,不同模量弯曲梁的弯曲刚度为

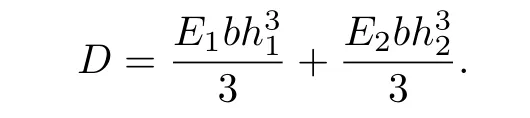
另外,可求得剪应力为

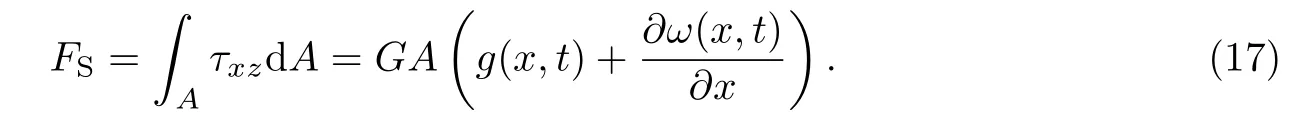
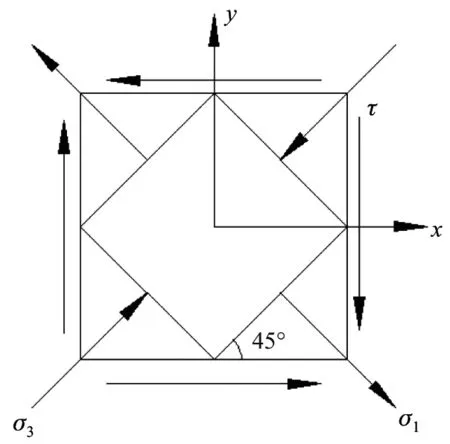
图2 纯受剪示意图Fig.2 Sketch of pure shear state

3 振动微分方程

不同模量梁的中性轴不与梁纵向对称轴重合,故使横坐标轴与初始状态时的中性轴重合.由弹性力学理论可知,空间平衡微分方程为

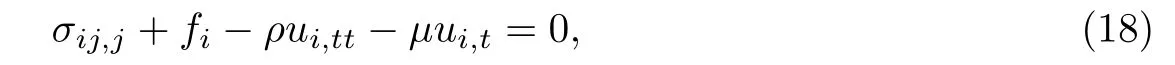
式中:ρ是密度,µ是阻尼系数;ui,tt,ui,t分别是ui对t的二阶导数和一阶导数,即加速度和速度;−ρui,tt,−µui,t分别表示惯性力和阻尼力,作为体积力的一部分出现在平衡方程中.若忽略阻尼,式(8)可写为

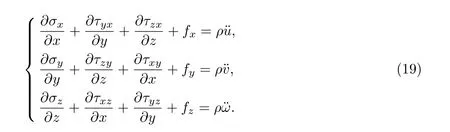
略去空间平衡微分方程中的体力,并对式(19)第一式各项乘以Z并对A进行积分,可得

式(20)中的第一项积分可化为

式(20)中的第二项积分可化为

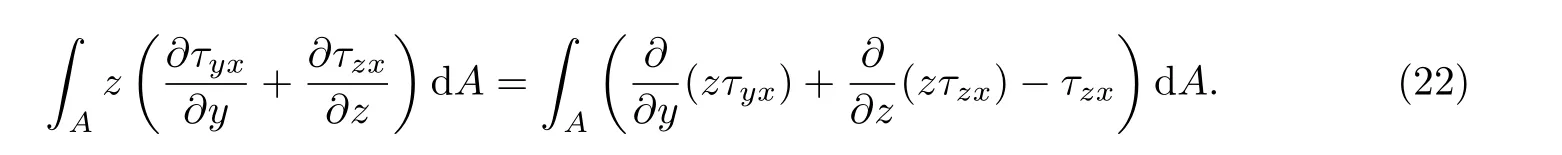
用高斯(格林)定理,把积分变为沿边界的积分,再运用边界条件简化,可得

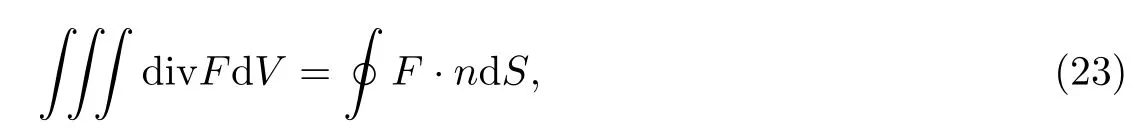
则式(20)中的第二项积分可化简为

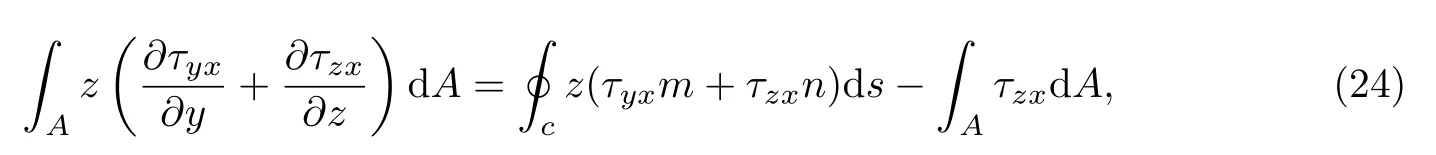
对于等截面直梁,则有l=0.

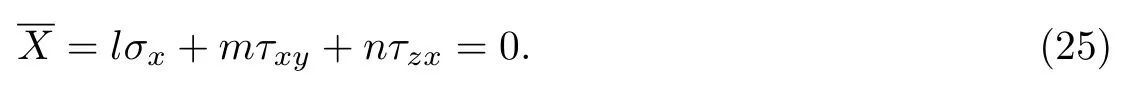
将式(25)代入式(24),可得

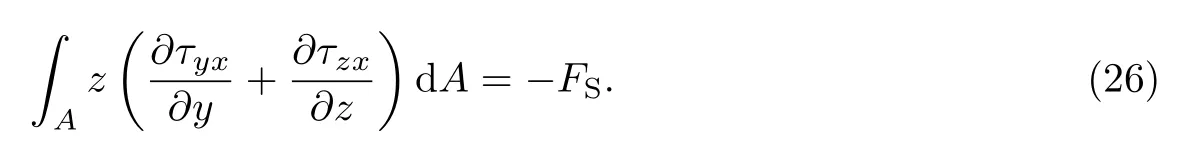
式(20)右边简化,可得

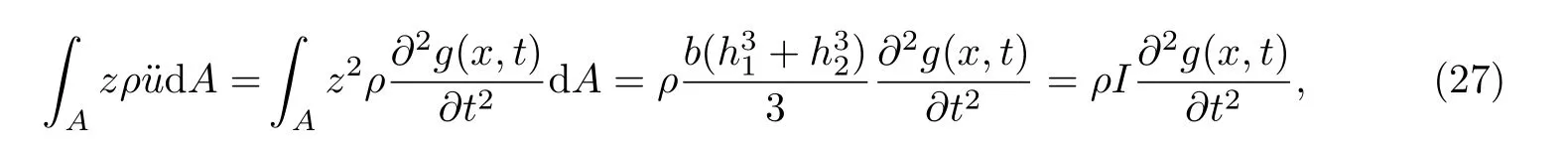
同理,将空间平衡微分方程中第三式略去体力,其他各项对A进行积分,可得

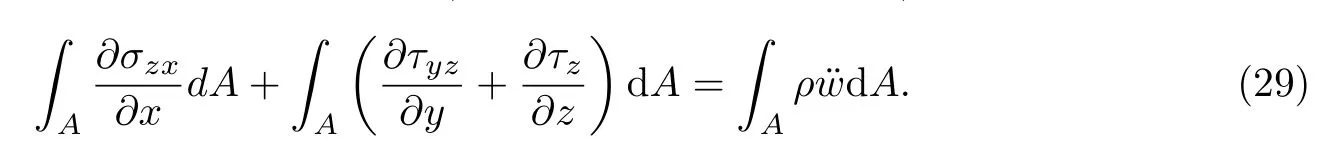
式(29)第一项可化为

第二项应用高斯定理,可化为

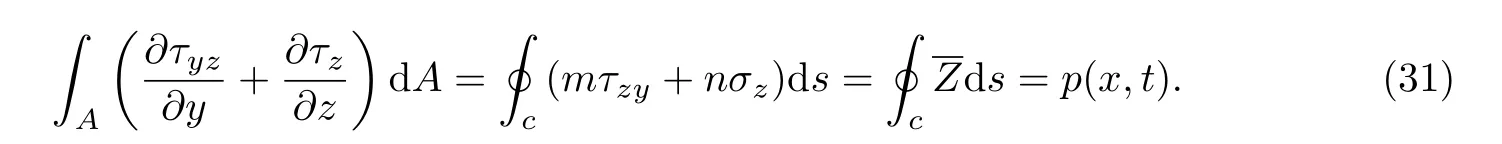
对式(29)右边简化,可得

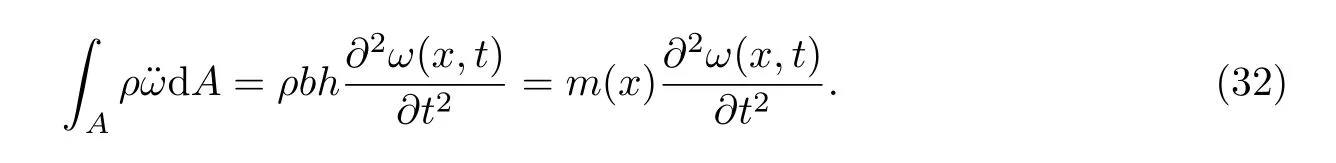
将式(30)和式(31)代入式(29),可得

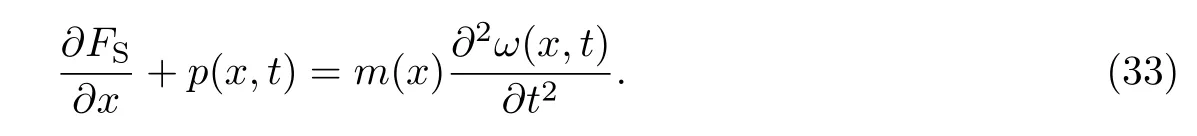
将M,FS代入式(28)和式(33),可得

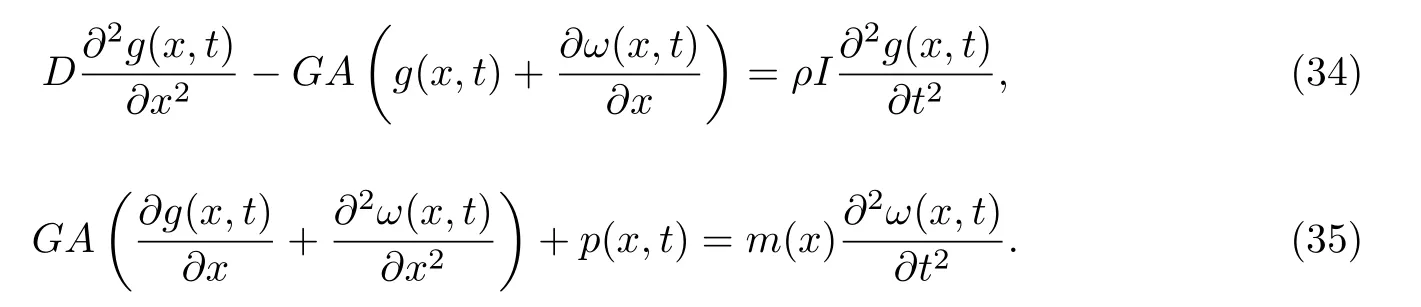
在实际计算中,一般引入剪切系数κ(表示截面上平均剪应变与截面形心处剪应变之比)简化模型,使理论更接近于三维弹性精确理论.

利用式(34),(35)及剪切系数κ,可以得到不同模量梁的振动微分方程为

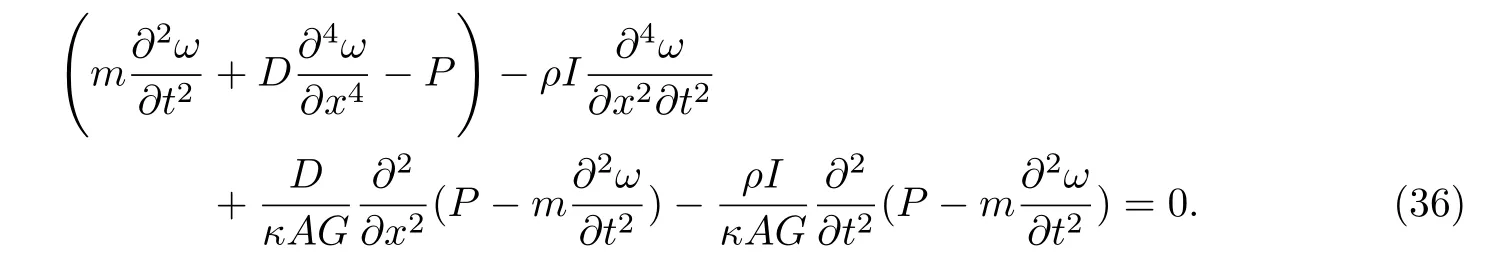
当忽略式(19)第一式中右边的惯性力时,则可得到欧拉-伯努利梁的振动微分方程为

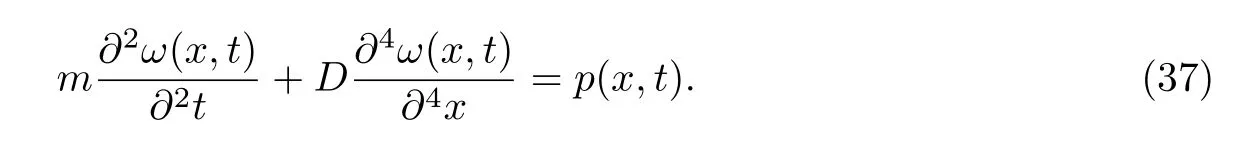
4 梁的自振频率和振型

当外荷载p(x,t)=0时,即可得到相应的自由振动方程为

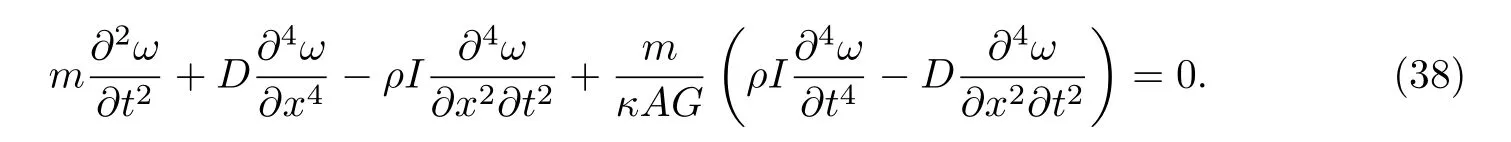
假设横向振动位移表达式为

将式(39)代入式(38),简化可得

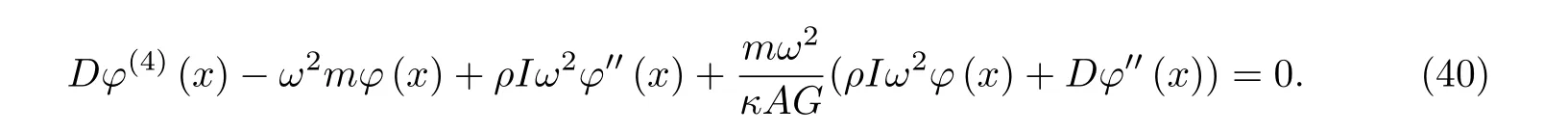
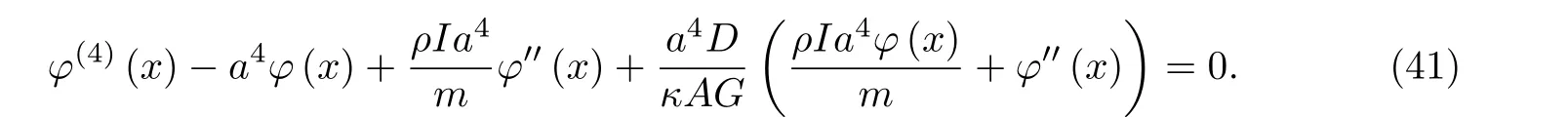
设式(41)解的形式为

将式(42)代入式(40),可得

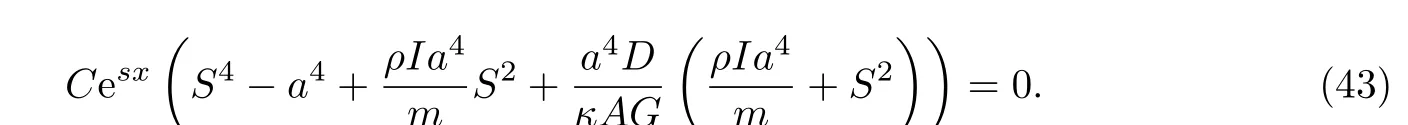
求解式(43),可得

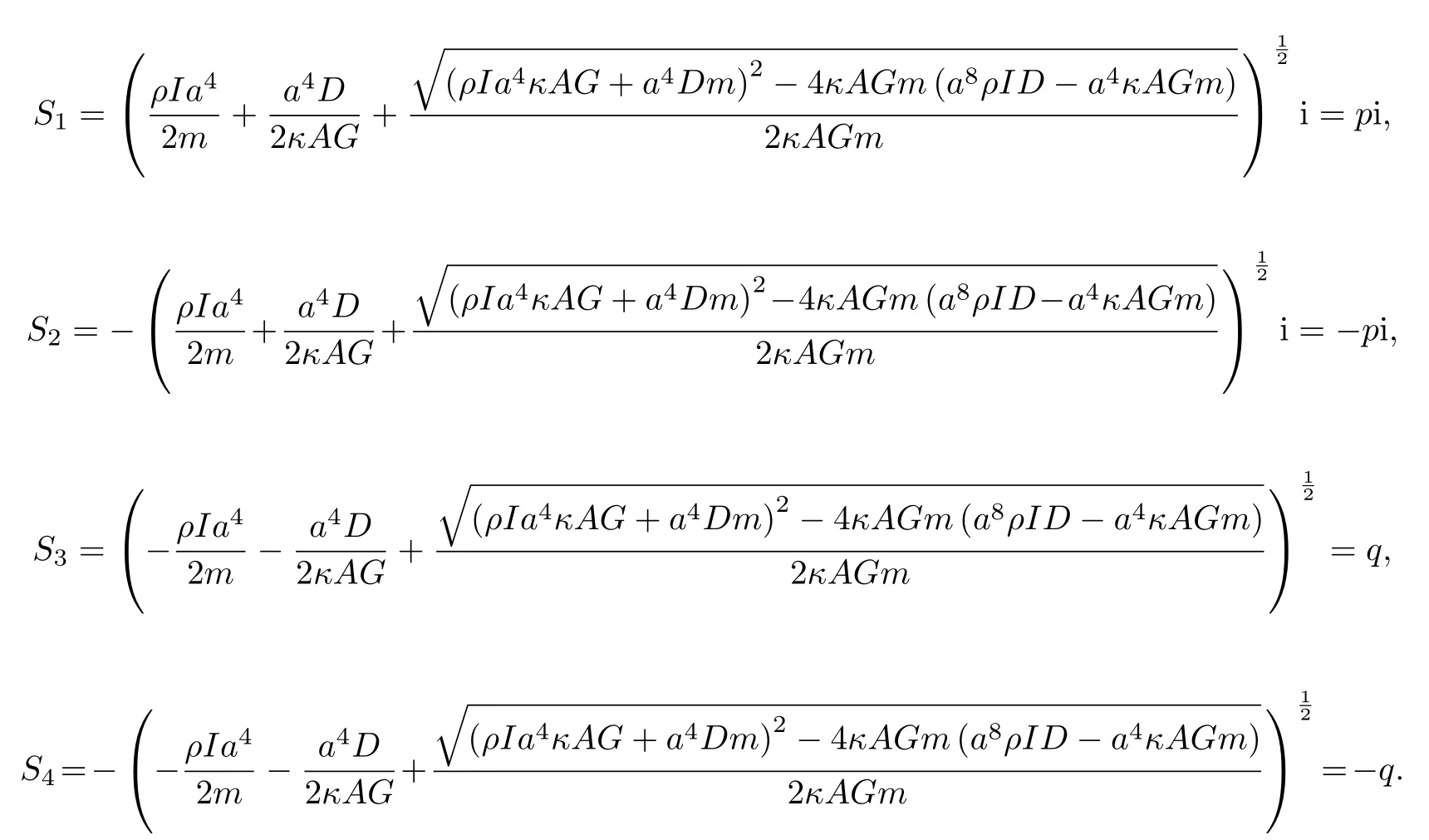
因此,式(41)的通解为

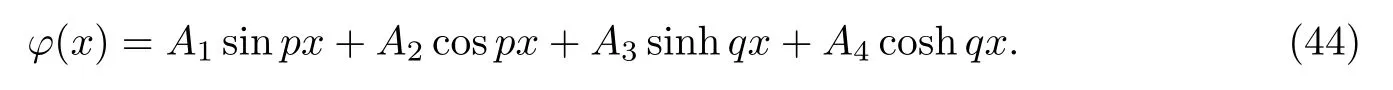
对于不同模量简支梁的自由振动,可知其边界条件为

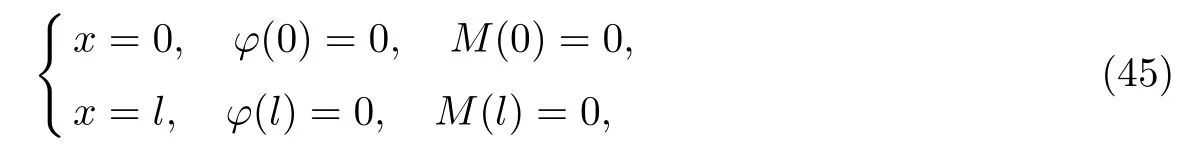
式中:M为弯矩.

把式(45)代入式(44),可以得到不同模量简支梁自由振动沿x轴方向的振型函数为

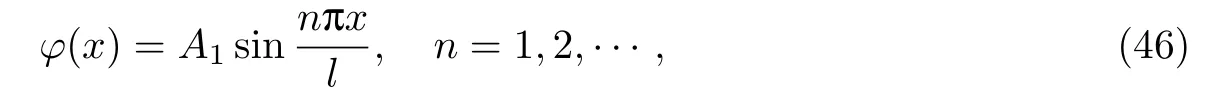
其固有频率为

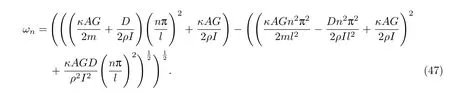
对于不同模量简支梁固有振动,由于每个周期的前半波段的中性轴与x轴方向重合,所以振型函数为式(46).而每个周期的前半波段中性轴的波型与后半波段的波型相反,故后半波段中性轴的波型函数为

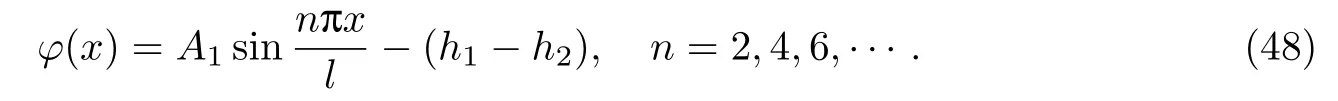
因此,不同模量简支梁自由振动时,n为奇数时波型表达式为式(46),n为偶数时为式(48).对于其他类型梁的自由振动,利用其边界条件,采用上述方法同样可以确定自由振动的振型函数和固有频率.

5 算例及结果分析

5.1 实例计算

简支梁b×h=0.3 m×0.6 m,梁长分别取3和12 m,,ρ=2.5×103kg/m3.

情况1 取实用梁,E1=25.5 GPa,ν1=0.27,E2=57 GPa,ν2=0.34;

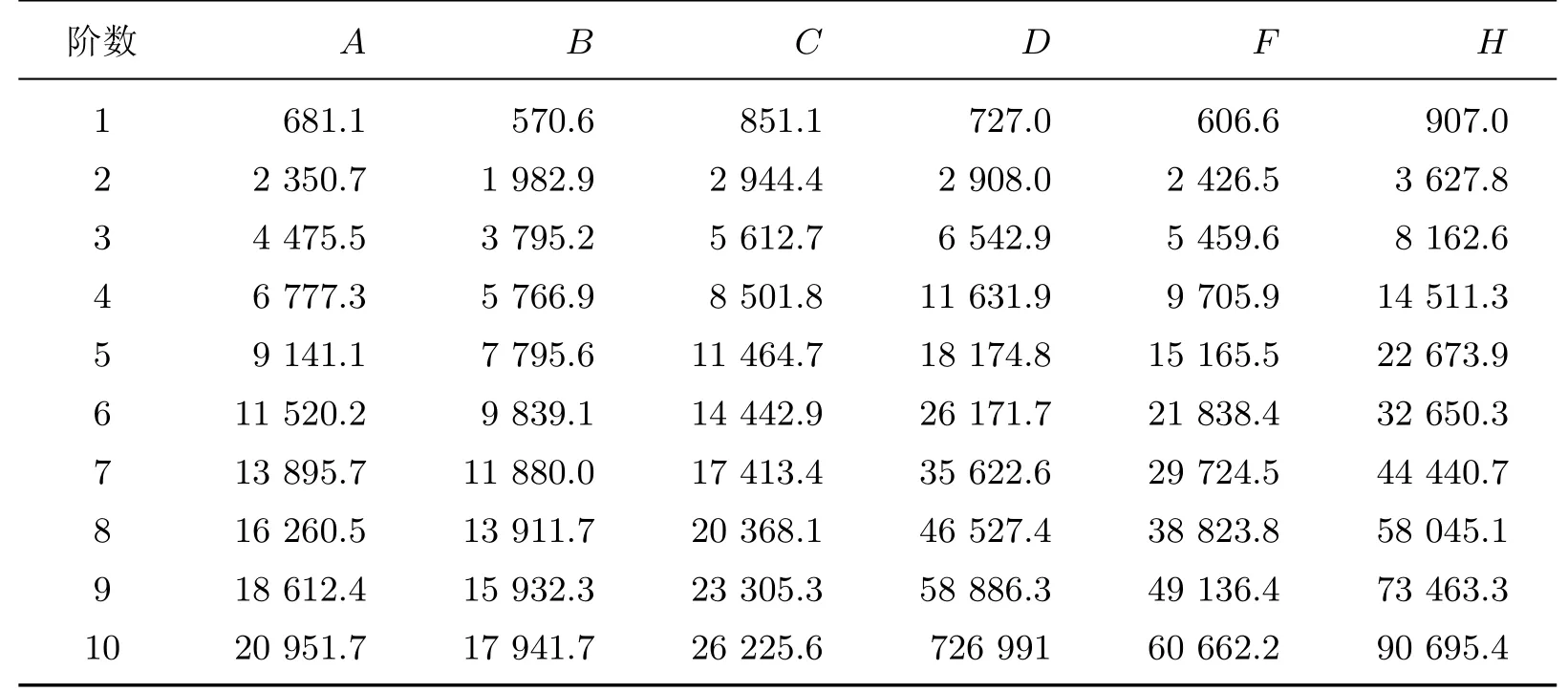
表1 梁长为3 m的不同模量简支梁固有频率ω(情况1)Table 1 Free frequencies of simply supported 3 m beam with different modulus(Case 1)

表2 梁长为12 m的不同模量简支梁固有频率ω(情况1)Table 2 Free frequencies of simply supported 12 m beam with different modulus(Case 1)

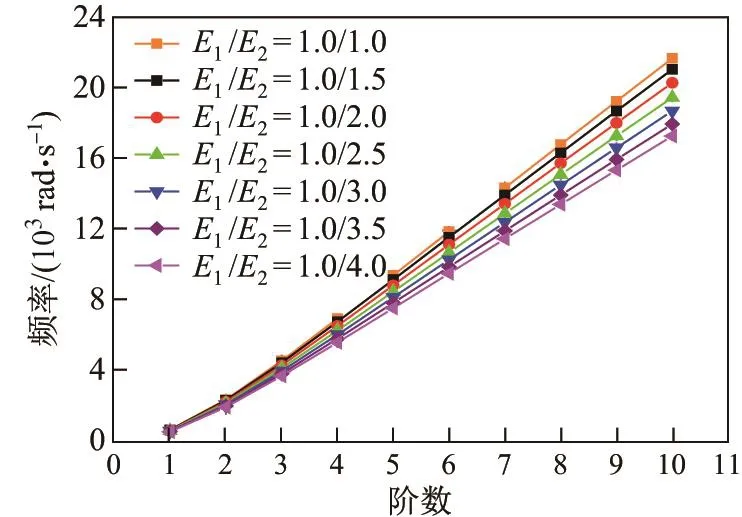
图3 梁长3 m按A计算所得固有频率(情况1)Fig.3 3 m beam based on the A calculate the free frequency(Case 1)

5.2 有限元结果对比

采用ABAQUS有限元软件对表1、表2中A,B情况进行模态分析,并提取各阶固有频率及模态振型.不同模量实用梁固有频率解析解与有限元软件数值解(见表3)进行比较,可以看出,两种计算结果接近,误差在2%以内,验证了解析的正确性.图4为简支梁三阶振型云图.由图4(a)和(b)可知,采用不同模量理论和相同模量理论分别模拟,得在两种理论模拟计算下的铁木辛柯梁的模态振型是相同的,但固有频率差距较大;由图4(c)和(d)可知,欧拉-伯努利梁也遵循相同的规律.

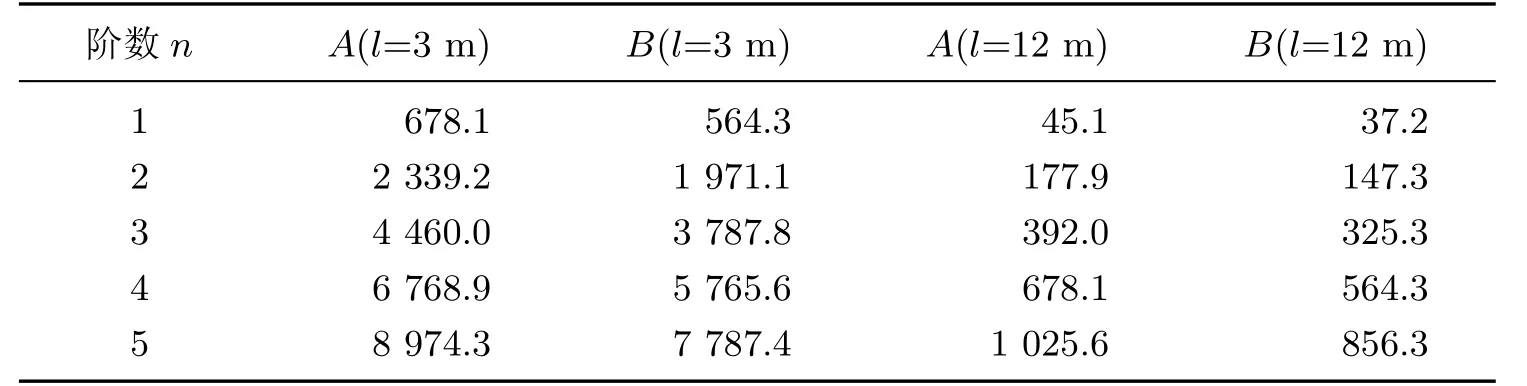
表3 通用有限元数值解ωTable 3 Numerical solution by FEMω

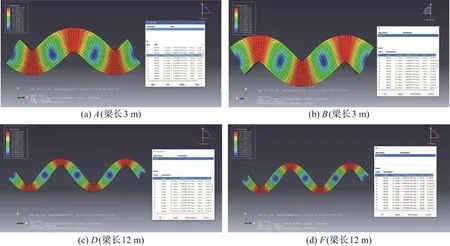
图4 简支梁三阶振型云图Fig.4 Cloud diagram of the beam

5.3 结果分析

对比表1和表2中的数据可知,对比不同拉压弹性模量梁与同模量梁,不论是铁木辛柯梁还是欧拉-伯努利梁,二者的固有振动频率误差均大于14%以上,最大约为25%,远远超出工程允许误差.这表明当拉压弹性模量相差较大时,应采用不同拉压弹性模量理论进行计算,可减小工程误差,保证结构的安全性.

由表1可知,考虑了不同拉压弹性模量后,当梁的高跨比为1/5时,梁固有频率计算误差由第一阶的6.7%上升至第十阶的247.0%.由表2可知,当梁的高跨比为1/20时,梁的固有振动频率计算误差呈递增形式,分别为第一阶0.4%,第二阶1.7%,第三阶3.9%,第四阶6.7%,第十阶34.5%.这表明:当梁的高跨比较小时,剪切效应对低阶固有振动频率的影响较小;随着阶数的增加,影响逐渐增大;当梁的高跨比较大时,剪切效应对固有频率的影响很大,不可忽略.

当截面的平均弹性模量保持不变,仅改变其分配时,梁各阶固有振动频率随E1/E2的增大而减小(见图3),这说明截面刚度的不均匀可使固有振动频率减小.当E1/E2=1/4∼1变化时,固有振动频率的误差最大可达到32%.对土木工程中广泛使用的混凝土材料,其拉压模量比一般为2.5.采用不同模量理论计算所得的固有频率小于同模量理论解,且误差随着阶数的增加而增大,平均误差为10%.

6 结束语

本工作研究了不同拉压弹性模量铁木辛柯梁的自由振动问题.利用不同拉压弹性模量材料纯剪切应力状态单元体,推导了不同拉压弹性模量剪切弹性模量表达式,建立了铁木辛柯梁的振动微分方程,推导计算了不同模量简支下的铁木辛柯梁的自由振动频率.另外,增加梁的跨高比,该解析模型可以退化为欧拉—伯努利梁的自由振动频率解析解.所求解的不同模量理论公式可完全退化到同模量理论公式,且与ABAQUS有限元软件模拟结果误差在2%以内,验证了解析结果的正确性.最后,讨论了不同模量理论计算结果与经典同模量理论计算结果的差异,得到了以下结论.

(1)考虑拉压不同模量时,中性轴在振动过程中发生跳变,使主振型函数成为分段函数,分为奇数波函数和偶数波函数.

(2)当拉压弹性模量相差较大时,不同模量理论计算所得的固有振动频率小于与经典模量理论解,且误差随着阶数的增加而增大,可达25%,远超工程允许误差范围.采用不同拉压弹性模量理论进行结构固有频率的计算,可减小误差,保证结构的安全性.

(3)对土木工程中广泛使用的混凝土材料,当计入其拉压不同模量后,相对于经典模量理论,二者的固有振动频率误差平均可达到10%.这对许多要避免产生共振的建筑结构会有较大影响,如铁路桥梁等.

(4)当截面的平均弹性模量保持不变,仅改变拉压弹性模量的大小,即结构的拉压模量不同,可以较大范围内改变梁的固有振动频率,同时拉压模量的不同(即刚度的不均匀)可使结构固有振动频率减小.在实际工程中,对拉压不同模量制备的结构,如应用经典的相同模量理论计算结构的振动问题,会存在安全隐患.