基于强度折减理论的加筋土边坡稳定性分析
2020-01-08张孟喜
顾 婕,张孟喜
(上海大学土木工程系,上海200444)
随着基础设施建设建设的加快,人们对边坡稳定问题日益关注,也涌现出了多种日益完善的边坡稳定分析方法.目前,边坡的稳定分析方法主要有极限平衡法和有限元强度折减法,其中极限平衡法包括圆弧滑动法、毕肖普法[1]、滑楔法、不平衡推力法以及Sarma法等.尽管极限平衡法中刚性墙的假定给计算带来了很大的简化,但由于与实际情况存在较大的差异,该方法仍具有局限性和不完善性.
近年来,对强度折减法的研究逐步涌现[2-4].由于强度折减法具有不需要假设,即可考虑岩土体内应力应变关系,自动求得任意形状的临界滑裂面和安全系数的优势,成为了目前边坡稳定分析中常用的方法[5-6].张鲁渝等[7]通过4组计算方案共106个算例,得出了强度折减法所得的安全系数高于简化毕肖普法的结论,并提出计算精度最为理想的情况.李春忠等[8]指出当塑性区趋于贯通且广义塑性应变和位移发生突变时,边坡处于破坏临界状态,此时的折减系数即为边坡的安全系数.李志佳等[9]结合强度折减法和灰色关联度理论对地层的物理、力学参数进行敏感性分析,得到如下结论:土体强度参数对边坡稳定性影响最显著,其次是边坡的几何参数,然后才是容重和坡后荷载;而弹性模量和泊松比不产生影响.张文杰等[10]利用强度折减法对加筋挡土墙进行稳定分析,研究了拉筋的内力和变形,并指出:随着埋置深度的增大,拉筋峰值拉力增大,峰值拉力点离面板距离减小,各拉筋峰值拉力点的连线近似为圆弧状.李林科等[11]结合强度折减法和极限平衡法在Geo-Studio的Sigma/w模块中进行强度折减,分析了典型的工程实例,提出以最大剪应力分布图与计算所得滑裂面为参考确定最可能滑裂面位置及形式,并在此基础上设计优化加筋高挡墙.栾茂田等[12]将强度折减有限元分析与计算结果图形实时显示技术相结合,验证了以广义塑性应变及塑性开展区作为边坡失稳判据的合理性.张陶陶等[13]结合有限元法对纯砂、水平与竖向加筋地基进行多组数值模拟,指出竖向加筋能使地基承载力显著提高,明显高于水平加筋.曲新杰等[14]基于有限元法,采用拟静力法研究了交通荷载下土工格栅加筋作用对路堤稳定性的影响,提出路堤合理加筋间距为1 m.此外,还有众多对加筋土结构的稳定性研究[15-17].然而,如何将加筋结构的稳定性与实际工程更好地结合还有待进一步研究.
本工作通过单一变量的模式进行,利用有限元数值模拟分析比较强度折减法与极限平衡法得出的素土边坡安全系数,并基于强度折减法对诸多可能影响素土坡和加筋土边坡稳定性的因素进行敏感性分析;然后,根据分析结果划分出主要影响因素以及次要影响因素,并总结这些因素对边坡稳定性的影响规律,为实际工程提供建议.
1 加筋边坡有限元建模
1.1 边坡加筋材料
本工作选用聚乙烯双向土工格栅作为边坡加筋材料,原因是其具有如下计算特点:①横肋和纵肋均具有较好的抗拉强度,并能对土体产生端承阻力作用;②结点能够对土颗粒提供侧向阻力;③网孔能够对粗颗粒土起到有效的嵌锁作用,并通过拱效应增大土工格栅和土颗粒之间的剪切阻力,提高整体稳定性.
均质路堤边坡示意图如图1所示.根据《公路桥涵设计通用规范》(JTG D60—15),车道荷载定为q=7.875 kN/m.路堤边坡土体材料参数见表1,其中γ为重力密度,c为黏聚力,φ为摩擦角,E为弹性模量,υ为泊松比.

表1 边坡土体参数Table 1 Physical parameters of the slope
土木格栅示意图如图2所示.以土工格栅的间距s,埋置深度d,长度l作为研究变量,具体的技术指标和尺寸参数见表2和3.根据基于平均场理论的格栅均匀化方法[18],一根肋条所附属的面积为S0=B2/2,如图2(b)所示.由于路堤边坡看作平面应变问题,故为方便考虑,计算土工格栅等效面积时取纵向1 m,由肋条数N可以得到土工格栅的有效作用面积S=NS0=NB2/2.根据土工格栅加筋长度8 m,厚度0.001 m可以得到单位宽度横截面为0.001 m2.
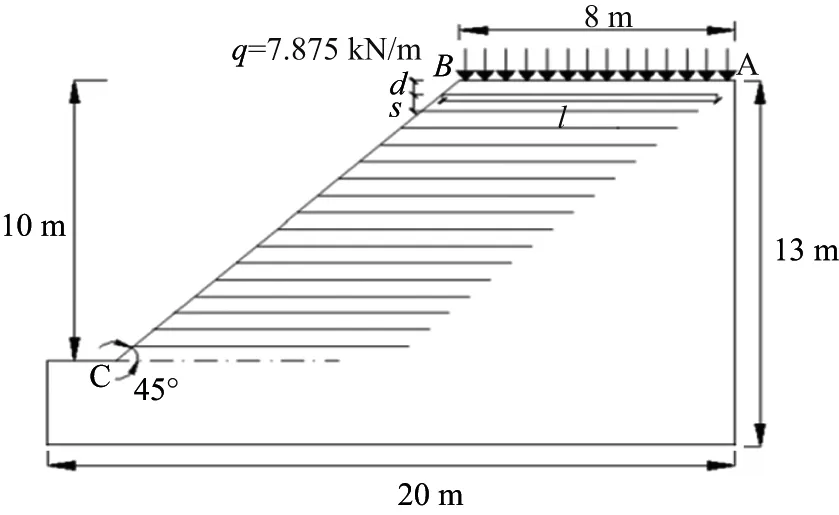
图1 加筋边坡示意图Fig.1 Sketch of reinforced slope
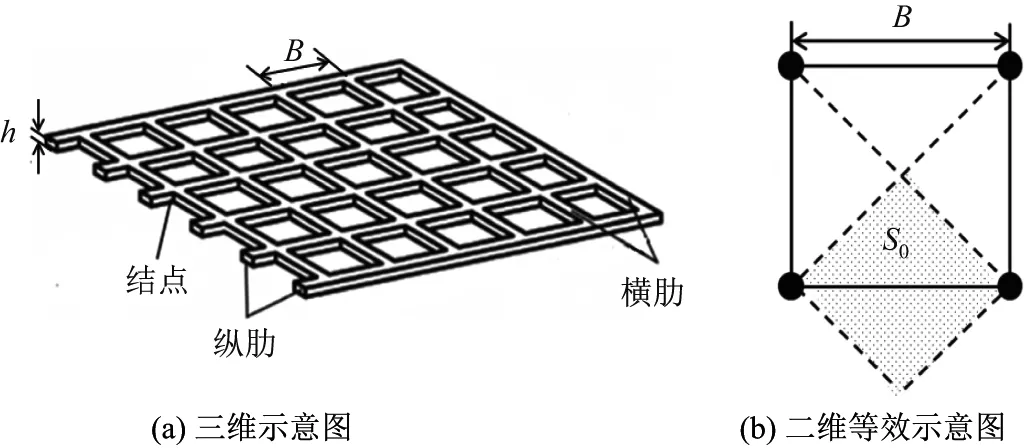
图2 土工格栅示意图Fig.2 Sketch of geogrid

表2 土工格栅技术指标Table 2 Technical specification of geogrid

表3 土工格栅尺寸参数Table 3 Dimension parameters of geogrid
1.2 有限元建模
1.2.1 模型建立
考虑到路堤较长的情况,本工作将路堤简化成平面应变问题进行研究.由于路基和路堤是对称结构,取一半实体建立二维平面模型.由于边坡和荷载关于路堤中心对称,对称面上水平位移基本为0,因此在边坡两侧设置为水平约束,底侧设置全约束.由于三角形网格是常应力、常应变单元,与实际情况不相符,故平面模型优先选择四边形网格.选择CPE4R四结点双线性平面应变四边形单元作为单元类型,划分后的模型示意图如图3所示.采用Mohr-Coulomb准则模型模拟土坡的塑性破坏.当在土坡中进行加筋时(见图4),土工格栅模型利用梁单元进行模拟,网格划分采用T2D2(二结点二维桁架单元).利用嵌入处理土工格栅与土体之间的接触,其中土工格栅作为嵌入区域嵌入到路堤边坡中.

图3 划分网格后的模型示意图Fig.3 Diagram of the model after dividing the mesh

图4 有限元分析中筋条布置图Fig.4 Layout of geogrids in finite element analysis
1.2.2 强度折减理论
强度折减法引入了一个场变量——强度折减系数.外荷载保持不变的情况下,边坡内土体可以提供的最大抗剪应力和外荷载在边坡内产生的剪应力之比即为边坡的安全系数.折减系数是对土体的抗剪强度指标进行折减,使得强度折减后边坡的最大抗抗剪应力和外荷载所产生的剪应力相等.当假定边坡内所有土体的抗剪强度发挥程度一致,折减后的土坡恰好发生破坏,则此时折减系数等于传统意义上的边坡的安全系数.
有限元中,将实际土体黏聚力c、摩擦角ϕ同时以系数F0

s进行折减,得到折减后的强度指标c0,ϕ’,并将其赋值给边坡进行数值计算.不断增大折减系数直至边坡达到临界破坏状态,此时的折减系数F0s即为该边坡的安全系数Fs.
2 加筋边坡稳定性影响因素
2.1 土体参数
边坡失稳的根本原因是土体某部分区域所受到的剪应力超过了自身所能够承受的范围,即抗剪强度值,从而造成该区域发生剪切破坏.因此,边坡失稳的原因可以总结为两方面:①土体承受的剪应力增加;②土体自身抗剪强度降低.
从土体的角度看,众多的因素包括边坡的几何参数坡高和坡角、土体的强度参数黏聚力和内摩擦角、土体的弹性模量和泊松比以及土体的重力密度、孔隙比和含水率等都会造成坡体所受剪应力或抗剪强度的变化,从而影响边坡的稳定性.本工作分别研究了不同的边坡比、黏聚力、内摩擦角、弹性模量下的边坡稳定性,共采取了13组工况,如表4所示.
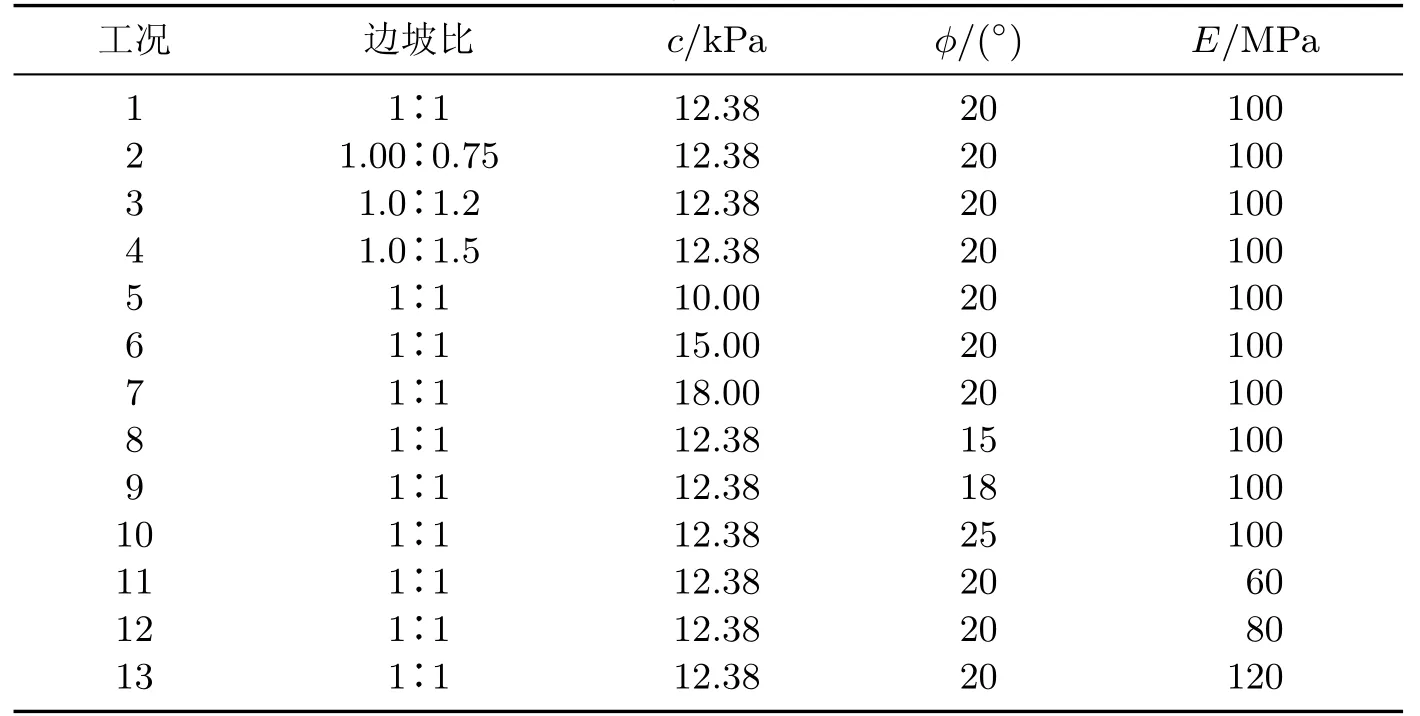
表4 土体工况Table 4 Working conditions of the soil
2.2 土工格栅参数
根据土工格栅的作用机理可以看出,加筋边坡主要是依靠土工格栅与土颗粒之间的相互约束来提高边坡整体的抗剪强度值,从而提高边坡的稳定性.只有当拉筋被拔出或筋材断裂时,土体才会失稳破坏,因此筋材的长度需要满足抗拔稳定性的计算要求.除此外,影响筋土相互作用力的因素还包括:土工格栅的网格尺寸,抗拉强度,延伸率以及加筋的方式,如:土工格栅加筋的位置、加筋间距和筋材长度等.本工作选取土工格栅的长度、间距以及埋置深度作为研究对象共设计了10种工况,如表5所示.采用单一变量的方式,通过数值模拟比较分析,研究了土工格栅的布置方式对边坡稳定性的影响.
3 边坡稳定性分析
3.1 土体参数对安全系数的影响
以边坡比为例,图5是1∶1.5边坡的塑性和位移云图.比较分析不同边坡比的云图,可以得出:路堤边坡达到破坏状态时,塑性区域的宽度随着边坡比的增大而明显变宽;最大综合位移发生在坡脚处,且左侧坡体作为滑动楔体沿着破裂面整体下滑.根据不同的边坡比对应的安全系数(见图6)可以看出,随着坡度放缓,安全系数逐渐增大,这是因为随着坡度变缓,边坡破坏时的滑动面后移,变为深层滑动,滑动面的长度变长,且抗滑力和下滑力的比值变大,故安全系数也随之增大,边坡稳定性得到提高.
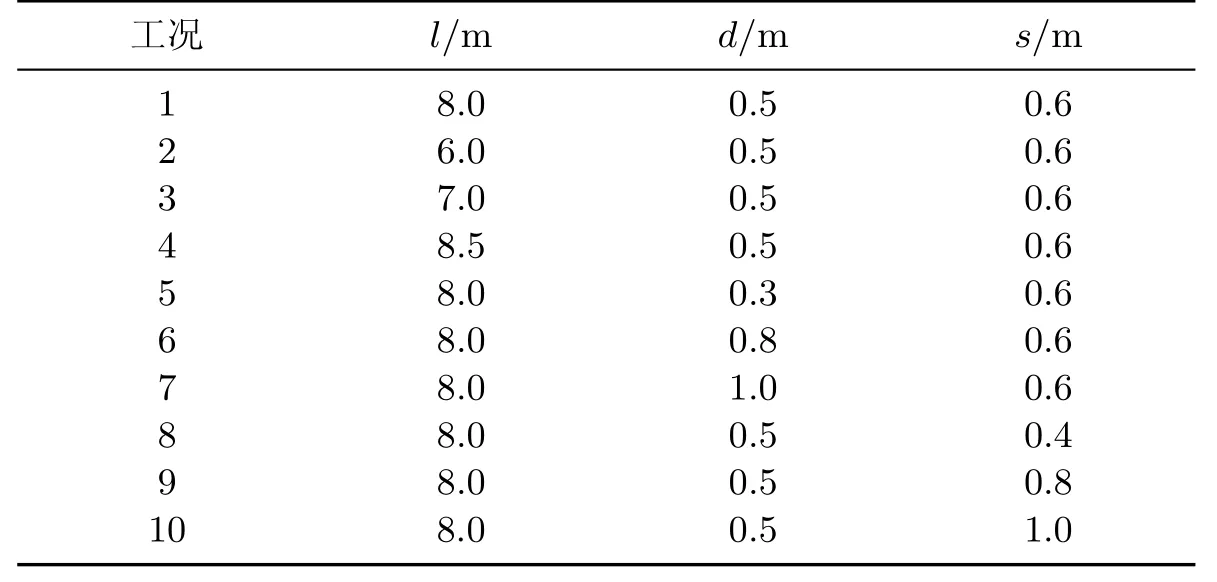
表5 土工格栅工况Table 5 Working conditions of the geogrids
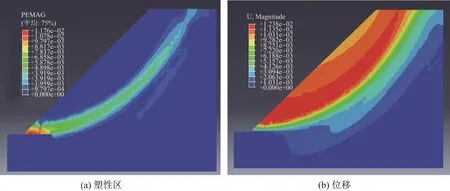
图5 未加筋边坡塑性区及位移云图(边坡比1.0∶1.5)Fig.5 Contours of the unreinforced slope(slope ratios:1.0∶1.5)
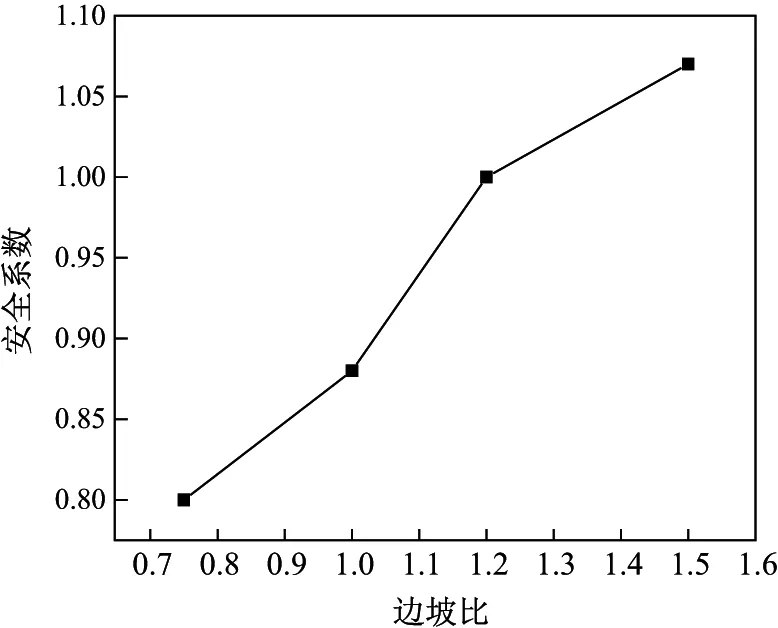
图6 安全系数随边坡比的变化Fig.6 Safety factors versus slope ratios
同样地,对于边坡填土的黏聚力、内摩擦角以及弹性模量对边坡稳定性影响的研究,在边坡比为1∶1的前提下,可以根据已经设计好的不同工况进行模型分析,最终对应的具体的安全系数详见表6.比较分析数值模拟的结果,可以总结得到它们对边坡稳定性的影响规律以及敏感程度.
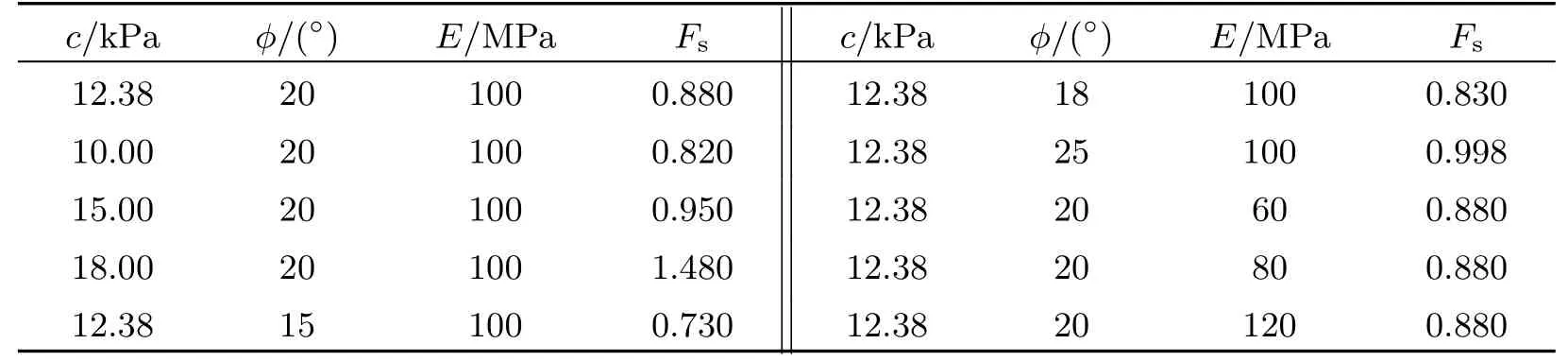
表6 未加筋边坡安全系数Table 6 Safety factors of the unreinforced slope
从表6可以看出:路堤土坡的安全系数随着黏聚力的增加而增大;当土体黏聚力增大时,即土颗粒之间的相互作用力变大,土体发生滑动时的阻力也相应增大,故边坡的稳定性得到提高;当土体内摩擦角值的增加时,安全系数逐渐增大,且增加的速度基本保持平稳.这是因为土的内摩擦角反映的是土的摩擦特性,当土的内摩擦角增大时,可以认为土体的摩擦力以及咬合力都相应增大,故边坡的稳定性得到了提高.当土体弹性模量逐渐增大时,安全系数维持不变,这是因为土体弹性模量代表应力和应变之比,弹性模量的变化影响变形场,但不会造成应力场的变化,而安全系数的定义是依赖于应力场的.因此,弹性模量变化会造成位移的变化,却不会对边坡安全系数产生影响[9].
3.2 土工格栅对安全系数的影响
以土工格栅的长度为例,图7为土工格栅l=8.5 m时的边坡塑性和位移云图.对比其他长度土工格栅对应的云图可以发现:随着土工格栅长度的增加,滑动面整体后移变成深层滑动,滑动面的长度和宽度均增大,塑性区绕过加筋区一直发展直至贯通坡体;但l=6.0 m和7.0 m时,土工格栅随滑裂面内的土体一起下滑,最大位移点仍发生在坡脚;当l=8.0 m或8.5 m时,最大位移发生在坡顶右侧未加筋的部分.
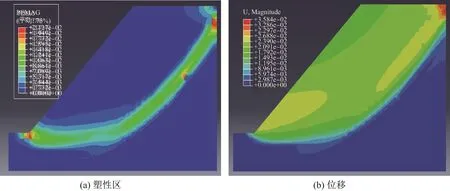
图7 加筋边坡塑性区及位移云图(l=8.5 m)Fig.7 Contours of the reinforced slope(l=8.5 m)
安全系数随格栅长度的变化如图8所示.可以看出,随着土工格栅长度的增大,加筋边坡的安全系数逐渐增大,土工格栅能够很好地对危险土体起到约束作用,阻碍边坡失稳,提高边坡的稳定性.但若筋材的长度只是略超出素土坡时的塑性发展区域,则无法很好地对滑移面起到约束阻碍的作用,土工格栅会随着潜在滑裂面内的土体一起下滑,起不到明显的加固作用.但无论土工格栅长度如何,加筋后边坡的安全系数总会有所提高.
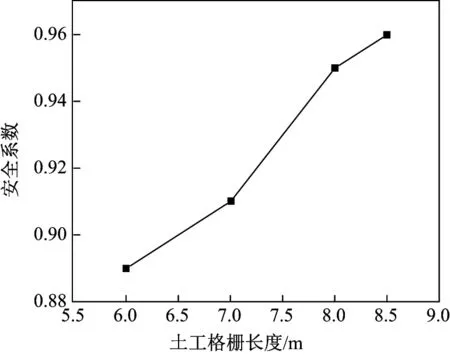
图8 安全系数随格栅长度的变化Fig.8 Safety factors versus lengths of geogrids
加筋边坡安全系数见表7.可以看出,埋置深度与安全系数没有明确的规律,相较于土工格栅埋置深度d=0.8 m,不论是减小为0.5 m,亦或是增大为1.0 m,其对应的边坡安全系数均有所减小.这是因为随着加筋位置的改变,土工格栅对未加筋时产生塑性应变区域的约束作用也相应改变.当最上层土工格栅距离坡顶为0.8 m时,最底部一层土工格栅与其上层土工格栅正好围住了相同条件下素土坡的最大塑性应变区域,故有效地限制了该区域塑性应变的发展,使得最大塑性应变区域发生转移,边坡发生滑动受到的阻力变大,相应的边坡稳定性也得到了提高.
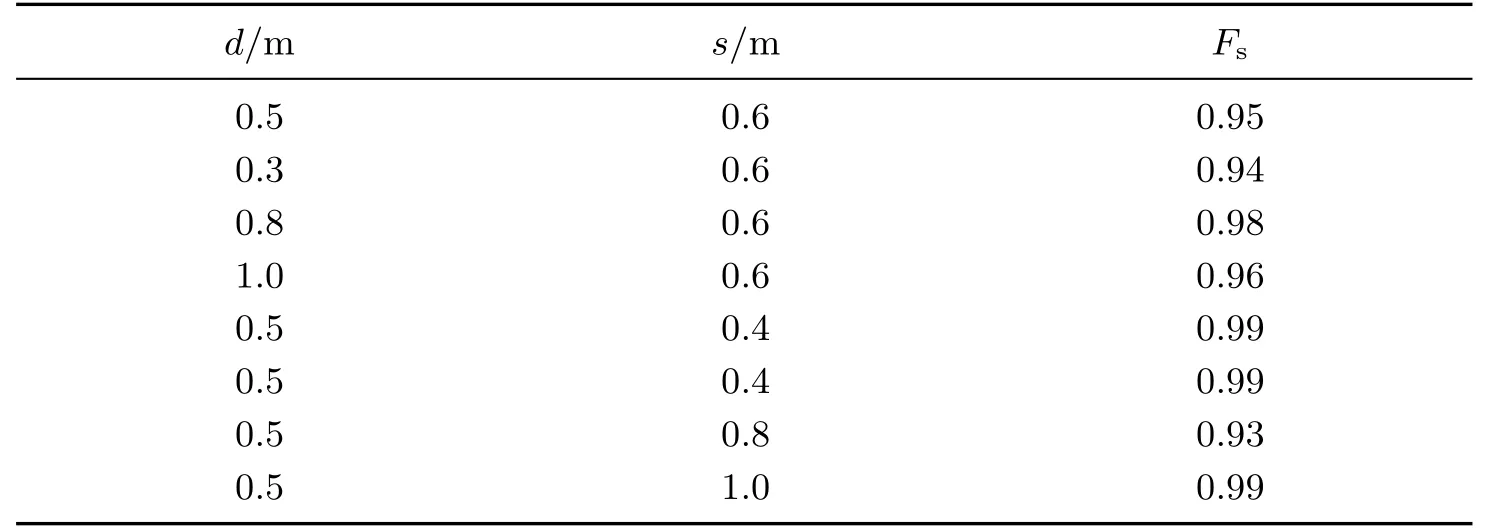
表7 加筋边坡安全系数Table 7 Safety factors of the reinforced slope
随着土工格栅间距的增大,加筋路堤边坡的安全系数逐渐减小直至基本不再发生变化.这是因为随着加筋间距的减小,一定的坡体高度范围内土工格栅的分布越密集,所占的比例也越大,相应的能够承担的拉力随之变大,故土体发生滑动相对愈加困难,边坡的稳定性也就随之提高.
土工格栅的埋深和间距是实际工程中可灵活控制的参数,对二者进行正交分析,计算结果如图9所示.计算结果表明:随着间距的增大,安全系数逐渐减小,而随着埋深的增大,安全系数先增大后减小;当埋深为0.8 m,间距为0.4 m,边坡的安全系数最大为1.14;当格栅间距较大时,安全系数随着埋深的变化较为平缓,而格栅间距较小时,安全系数随格栅埋深的变化逐渐趋于显著,尤其是格栅间距为0.4 m时,安全系数变化最为显著,此时格栅埋深从0.5 m增至0.8 m,安全系数从0.99增至1.14(增长15.2%).埋深和间距正交分析结果见表8.可以看出:当格栅埋置深度为0.8 m时,边坡安全系数均高于同等布置间距下其他计算结果.故当格栅埋深合适时,可以适当增大格栅的间距,在保证边坡稳定性的同时,提高其经济性.
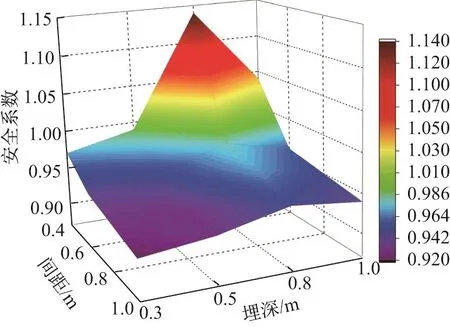
图9 埋深和间距正交分析云图Fig.9 Contour of orthogonal analysis on spatial arrangement

表8 埋深和间距正交分析Table 8 Results of orthogonal analysis
综上所述,对同一土坡进行加筋,不论其铺设方式如何选择,筋材总能在一定程度上限制素土边坡中塑形区的发展,从而提高边坡的稳定性.加筋时筋材的铺设方式对素土边坡稳定性的提高存在显著差异,安全系数增幅从1.14%至29.5%.由此可见,合理地选择土工格栅的铺设方式可明显地提高素土边坡的稳定性.
4 参数敏感性分析
4.1 土体参数对边坡位移的影响
在分析边坡的稳定性时,折减系数决定了计算时边坡的强度,直接影响着边坡的位移、应力分布和塑性区的发展.故对各参数进行敏感性分析时,选取各参数组中最小的安全系数值对边坡强度进行折减.计算结果表明素土坡的塑性区发生在靠近BC面处,地表沉降最大值出现在B点附近.最大位移发生在坡脚附近,所以侧向位移的最大值出现在C点附近,且相较于坡脚附近,BC面其他位置的侧向位移均明显较小,并且随着计算点至AB面距离的减小而减小.
(1)土体弹性模量.土体弹性模量对地表沉降和侧向位移的影响如图10所示.随着弹性模量的增大,地表的沉降明显减小,同时因为土体弹性模量的增大导致土体的强度的增加,所以在地表沉降减小的同时侧向位移也相应的减小.相较而言,地基最大沉降的减小幅度与路堤外侧拱起值的减小幅度基本一致,均约为50%.
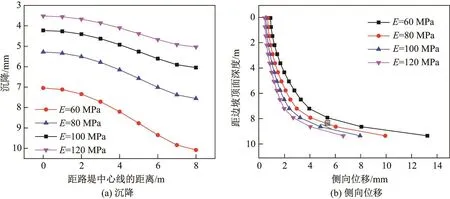
图10 弹性模量对边坡变形的影响Fig.10 influence of elastic modulus on settlement and lateral displacement
(2)其他土体参数.其他土体参数对地表沉降和侧向位移的影响如表9所示.从表中可以对比看出,边坡比为1∶0.75时,地表AB面的的沉降以及BC面的侧向位移均远远大于其他3种工况.而边坡比自1∶1逐渐增大时,对地表沉降和侧向位移的影响均较为均匀,而坡脚处的侧向位移明显高于其他位置.随着边坡放缓,地表的沉降明显减小,还可以限制土体的侧向位移和路堤外侧的隆起,提高路堤的整体稳定性.
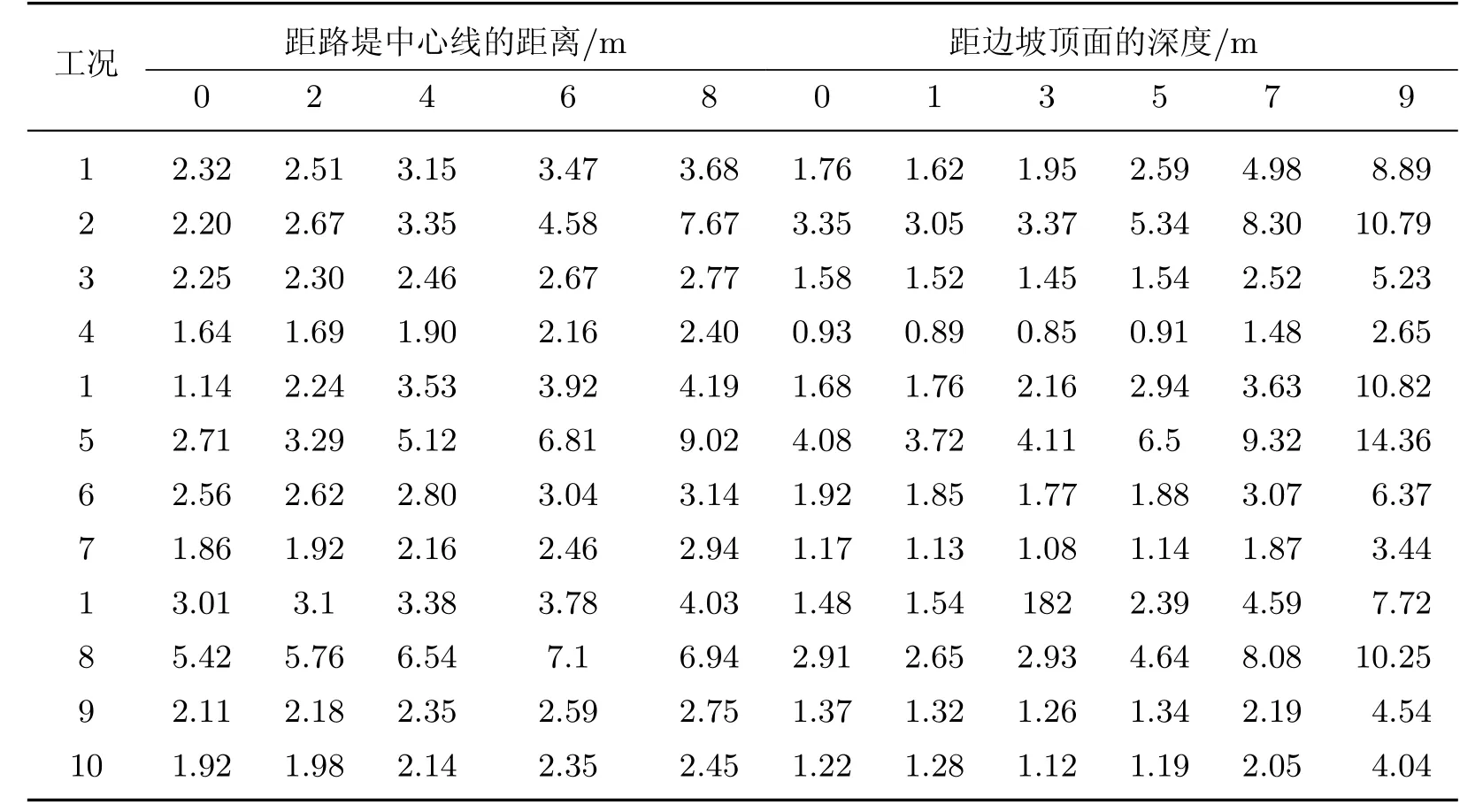
表9 未加筋边坡变形结果Table 9 Deformations of the unreinforced slope
对比土体黏聚力的4种工况可以看出:地表沉降和侧向位移随着土体黏聚力的增大而明显减小,边坡坡脚外侧的隆起也受到了限制;土体黏聚力提高了土颗粒之间的相互吸引力,使得在外荷载作用下,土颗粒之间发生相对滑移变得更加困难,由此限制了沉降及侧移,提高了路堤的整体稳定性.
根据内摩擦角4组工况的对比分析可以看出,随着内摩擦角的增大,地表的沉降和土体的侧向位移均明显减小.内摩擦角增大使得土颗粒之间发生相对滑移时受到了更大的阻力,使得在外荷载作用下土颗粒之间更难发生相对滑移,由此限制了沉降及侧移,提高了路堤的整体稳定性.另外,由上分析可以看出,改变土体的内摩擦角时,地表沉降和侧向位移减小的程度分别为64.7%和60.6%,明显小于相同条件下改变黏聚力减小的程度,因此要提高土体的稳定性,增大黏聚力比增大内摩擦角更为显著.
4.2 加筋对边坡位移的影响
对同一土坡进行加筋,选用弹性模量为10 GPa,长度为8 m的土工格栅,从埋深0.5 m处按间距0.6 m一直加至坡脚处,得到的地表沉降以及侧向位移如图11所示.从图中可以看到,土工格栅加筋不仅使得沉降明显减小,而且有效限制了土体的侧向位移和路堤外侧的隆起;加入土工格栅后,地表的沉降明显均匀,最大沉降减小了25.6%,最大侧向位移减小了31.8%,明显地提高了路堤的整体稳定性.
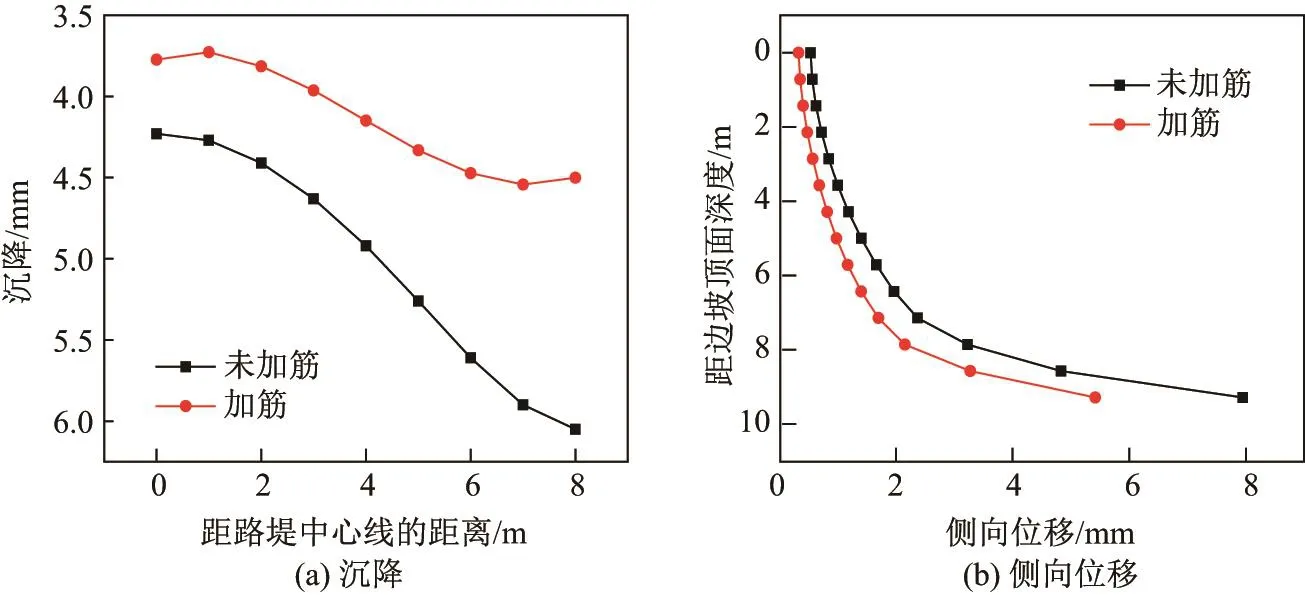
图11 加筋与未加筋边坡变形的对比Fig.11 Comparisons of slope with and without reinforcements on deformations
4.3 土工格栅参数对边坡位移的影响
(1)土工格栅间距.土工格栅的间距对地表沉降和侧向位移的影响如图12所示.由于加筋后,塑性区后移,所以地表沉降最大值不再发生在坡顶处,而是转移到AB面中部,故沉降图呈下凸状.从图12中可以看到,随着间距的减小,地表的沉降明显减小,边坡的稳定性得到提高.而由于加筋后边坡的最大位移发生在AB面未加筋处,且主要为竖向位移,故加筋后对沉降的改善作用显著,而对侧向位移的作用基本不变,所以侧向位移均较接近.
(2)其他土木格栅参数.其他土工格栅参数对地表沉降和侧向位移的影响分别如表10所示.对比分析土工格栅长度的3种工况,可以看到:整体而言,加筋后地表沉降仍然发生在AB面中部,并且随着长度的增加,地表的沉降明显减小,而侧向位移差别不大,边坡稳定性得到提高;但当土工格栅的长度为6 m时,长度的影响趋势发生了变化.由于筋材的长度过短,影响边坡塑性区的范围相对靠近坡面,故当筋材为6 m时距路堤中心A点较近的区域沉降相对较小,随着距A点距离的增加沉降逐渐增加.
在长度、间距和铺设层数均一定的情况下,随着埋置深度的增加,地表的沉降明显减小,而侧向位移差别不大.这是由于在其他条件相同的情况下,随着埋置深度增大,底部的土工格栅更接近坡脚的塑性区域,能够更好地限制土体产生位移,边坡的稳定性得到提高;而当土工格栅的埋置深度为0.8 m时,由于土工格栅影响的塑性区范围和其他3种工况相比恰好较小,对土体发生位移的限制能力较弱,因此地表的沉降要高于其他3种工况.
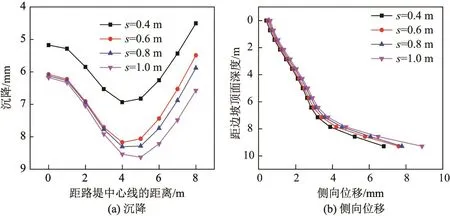
图12 加筋间距对边坡变形的影响Fig.12 influence of reinforcement spacing on settlement and lateral displacement
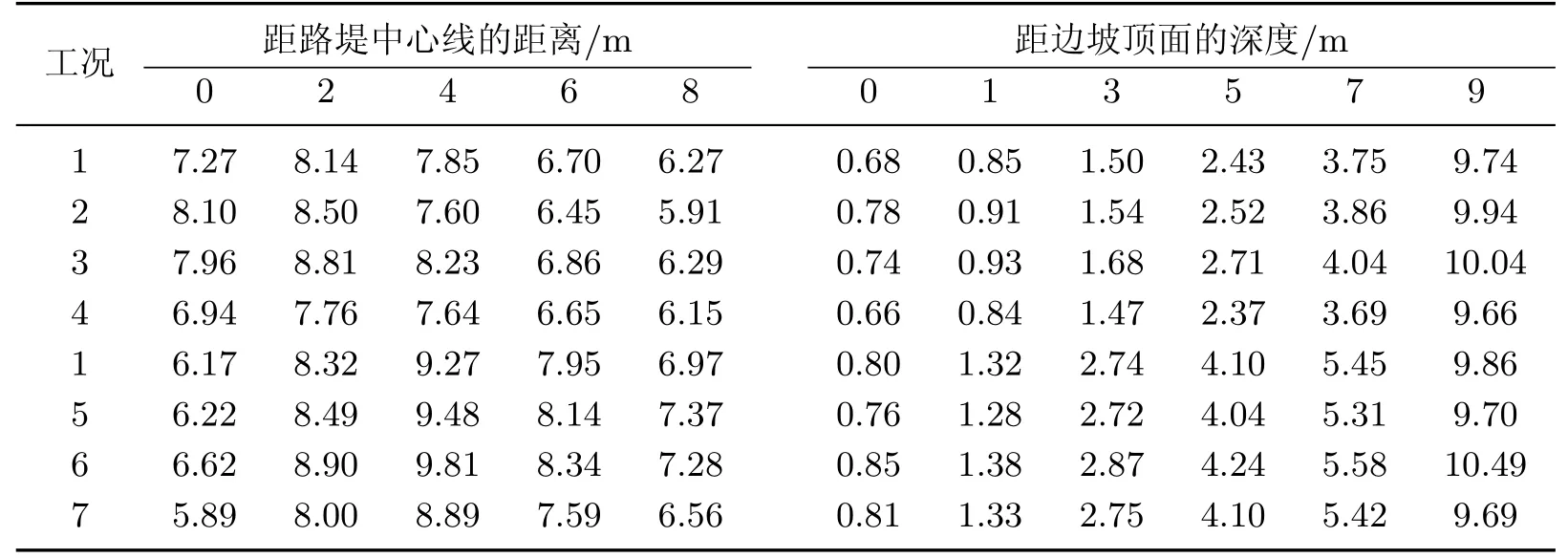
表10 加筋边坡变形结果Table 10 Deformations of the reinforced slope
5 结束语
本工作通过数值模拟研究土体参数和筋材参数对加筋边坡稳定性的影响,得到如下结论.
(1)土体参数中边坡的安全系数对土体黏聚力的变化最为敏感,其次为内摩擦角和边坡比,而弹性模量不对其产生影响.
(2)筋材参数中土工格栅的长度更容易引起边坡稳定性的变化,且加筋时,长度不宜过短,否则筋材的约束作用将不能充分发挥,加筋效果将得不到体现.
(3)加筋边坡中筋材的间距越大,边坡的最小安全系数值越小;但当筋材的间距增大到一定的程度时,加筋的作用将得不到充分体现,其中边坡的安全系数将接近于相同因素条件的素土坡的安全系数值,并且不再减小.
(4)加筋边坡中加筋的位置也会对边坡的安全系数产生影响.当加筋的位置可以位于相同条件下素土坡失稳破坏时的塑形区域时,则能够很好地限制坡体危险土体的滑移,对变形起到约束作用,有效地提高边坡的稳定性.
(5)加筋固然能够提高边坡的稳定性,然而若实际工程许可,也可采用改变边坡比或者提高填土压实度改善土体的黏聚力和内摩擦角的方法提高边坡的稳定性.
