基于裂纹等效扭转弹簧模型的裂纹梁振动分析
2020-01-08王天宇
戴 缘,王天宇,杨 骁
(上海大学土木工程系,上海200444)
由于载荷的作用以及环境的影响,土木工程和机械工程的中重要构件——梁常常会出现裂纹,导致其承载力降低,使用寿命缩短.因此,研究裂纹梁的动静力学性能[1-5]及其裂纹的损伤识别对保证梁构件的正常服役具有重要的理论意义和应用背景[6-8].
研究裂纹梁静力变形和动力响应的一个经典方法是将裂纹等效为扭转弹簧,并以裂纹为界,将裂纹梁分为若干子梁段,各子梁段利用裂纹的等效扭转弹簧连接,得到裂纹梁的等效分析模型.在此基础上,每个子梁段利用梁模型进行求解,然后利用梁的边界条件以及裂纹处等效扭转弹簧的连续性条件确定待定系数,从而得到裂纹梁的变形响应[2,9-10].但这种求解方法每增加1条裂纹,其待定系数就增加4个,导致具体问题的求解较为繁琐.为此,人们提出利用矩阵传递法[7,11-12]以降低求解的复杂性,但是这种方法涉及较复杂的计算,难以给出形式简单的闭合解析解.
近年来,为简化分析和计算,基于裂纹的等效扭转弹簧模型,众多学者采用广义Delta函数刻画裂纹引起梁刚度的改变,并得到由Heaviside函数表示的显式闭合解.Buda等[13]以及Caddemi等[14-15]等采用负Delta函数刻画裂纹处梁刚度的变化,然而,该描述在物理上存在欠缺.为此,Palmeri等[1]和Caddemi等[16]采用正Delta函数描述裂纹处梁弯曲的柔度,从而避免了物理上的非完整性.考虑裂纹缝隙效应以及裂纹的开闭状态,孙嘉琳等[17]以及Yang等[18]从物理上建立了开闭裂纹梁的等效抗弯刚度,给出了了开闭裂纹梁静力弯曲的解析闭合解,而汪德江等[19]研究了Timoshenko梁中开闭裂纹位置及裂纹损伤的识别方法.
本工作研究开裂纹Euler-Bernoulli梁的动力特性和动力响应.首先,基于裂纹的等效扭转弹簧模型,利用Delta函数给出了裂纹梁的等效抗弯刚度,建立裂纹Euler-Bernoulli梁动力响应的初边值问题;其次,不同于裂纹梁动力控制方程求解的经典变易系数法[20-21],而是给出了一种较为简便的通解求解方法,并得到具有任意条裂纹Euler-Bernoulli梁振动模态的统一显示表达式.在此基础上,研究了不同边界条件下裂纹梁的动力特性,数值揭示了裂纹深度和数量等对裂纹梁动力特性的影响.最后,利用模态叠加法,分析了跨中集中简谐荷载作用下简支裂纹梁的动力响应,考察了裂纹深度对裂纹梁动力响应的影响,研究结果对梁裂纹的动力损伤检测具有一定的指导意义.
1 裂纹梁的自由振动
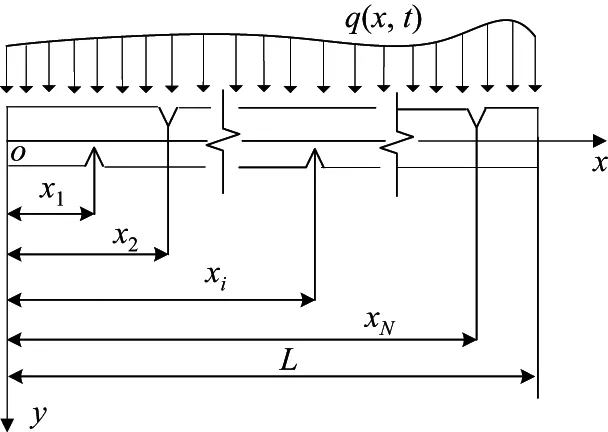
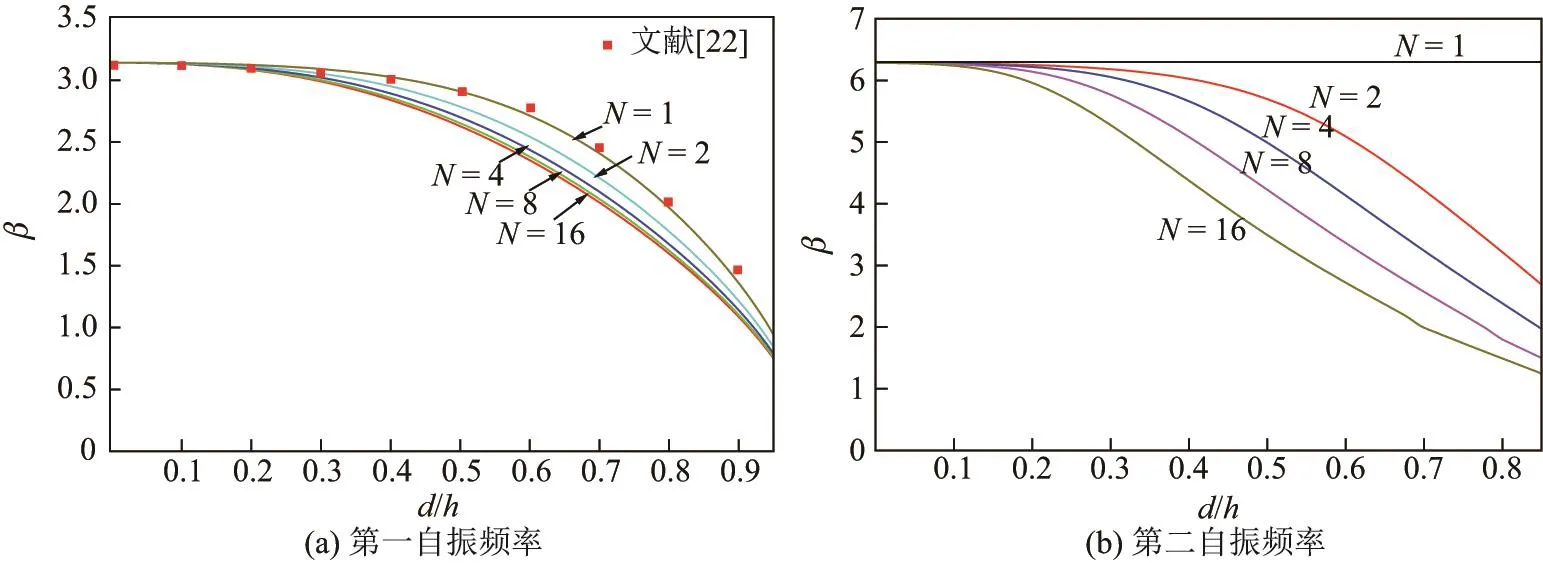
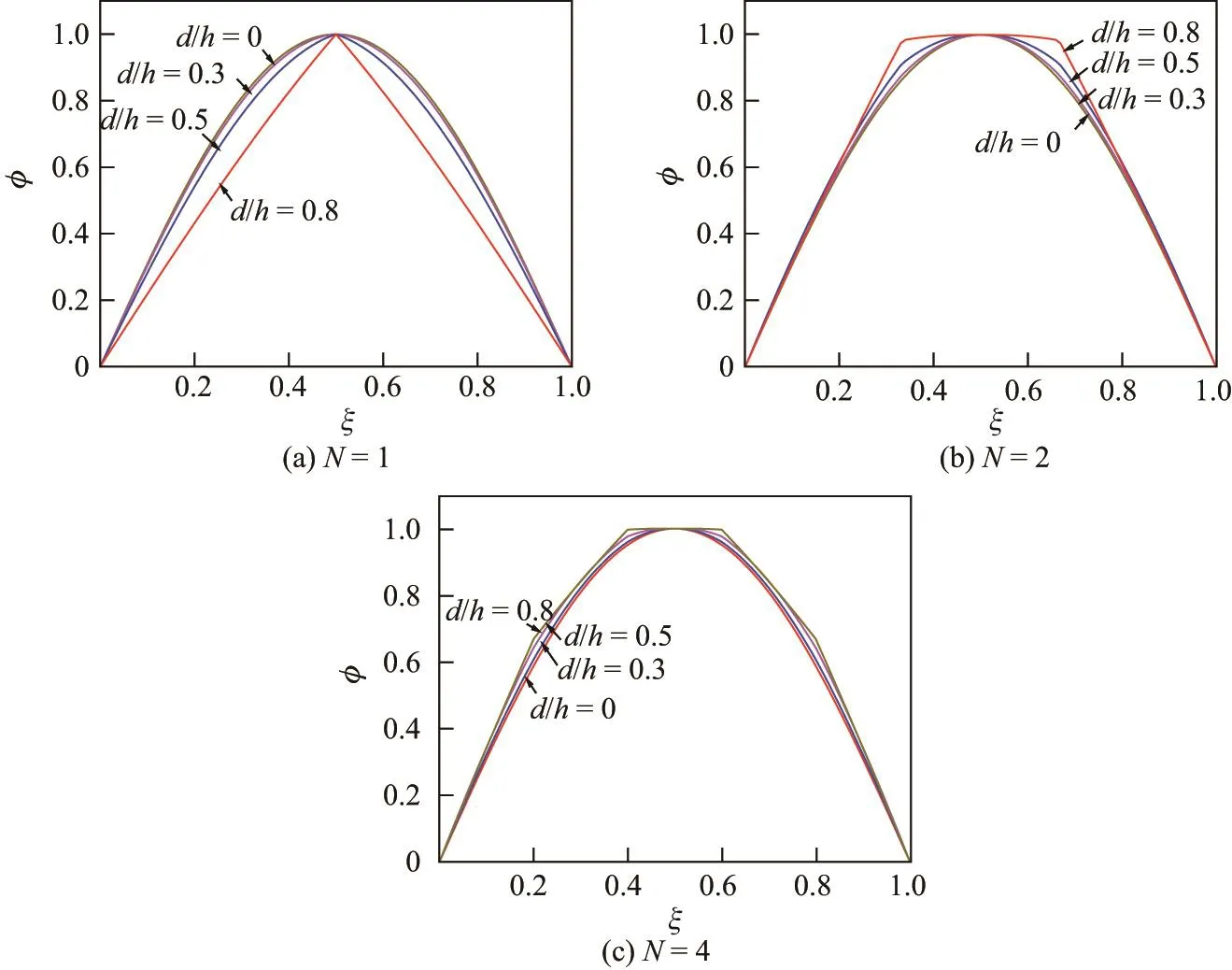
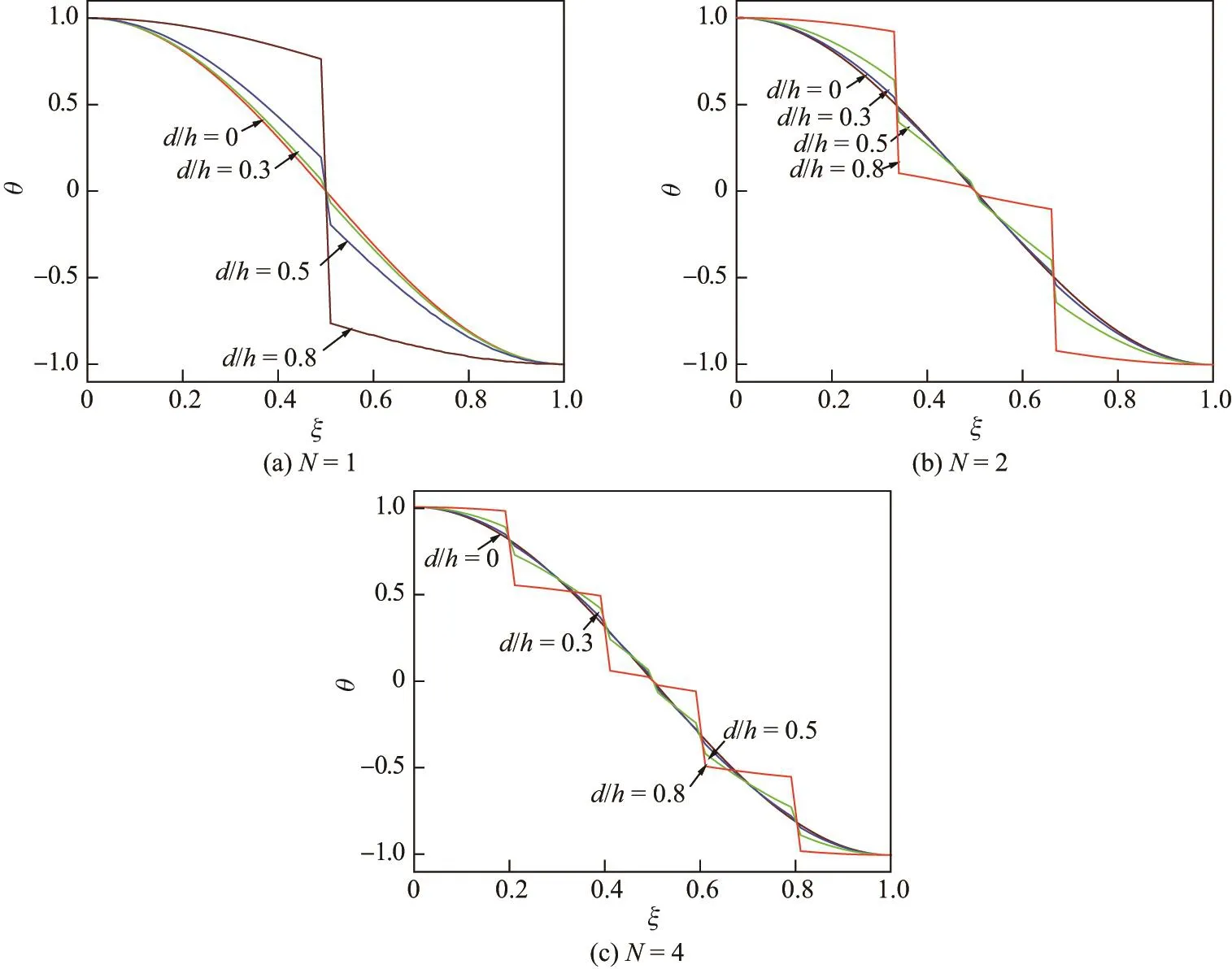
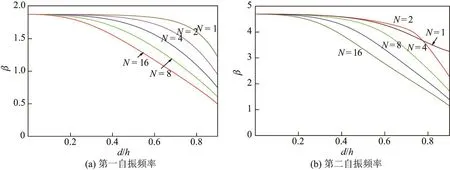
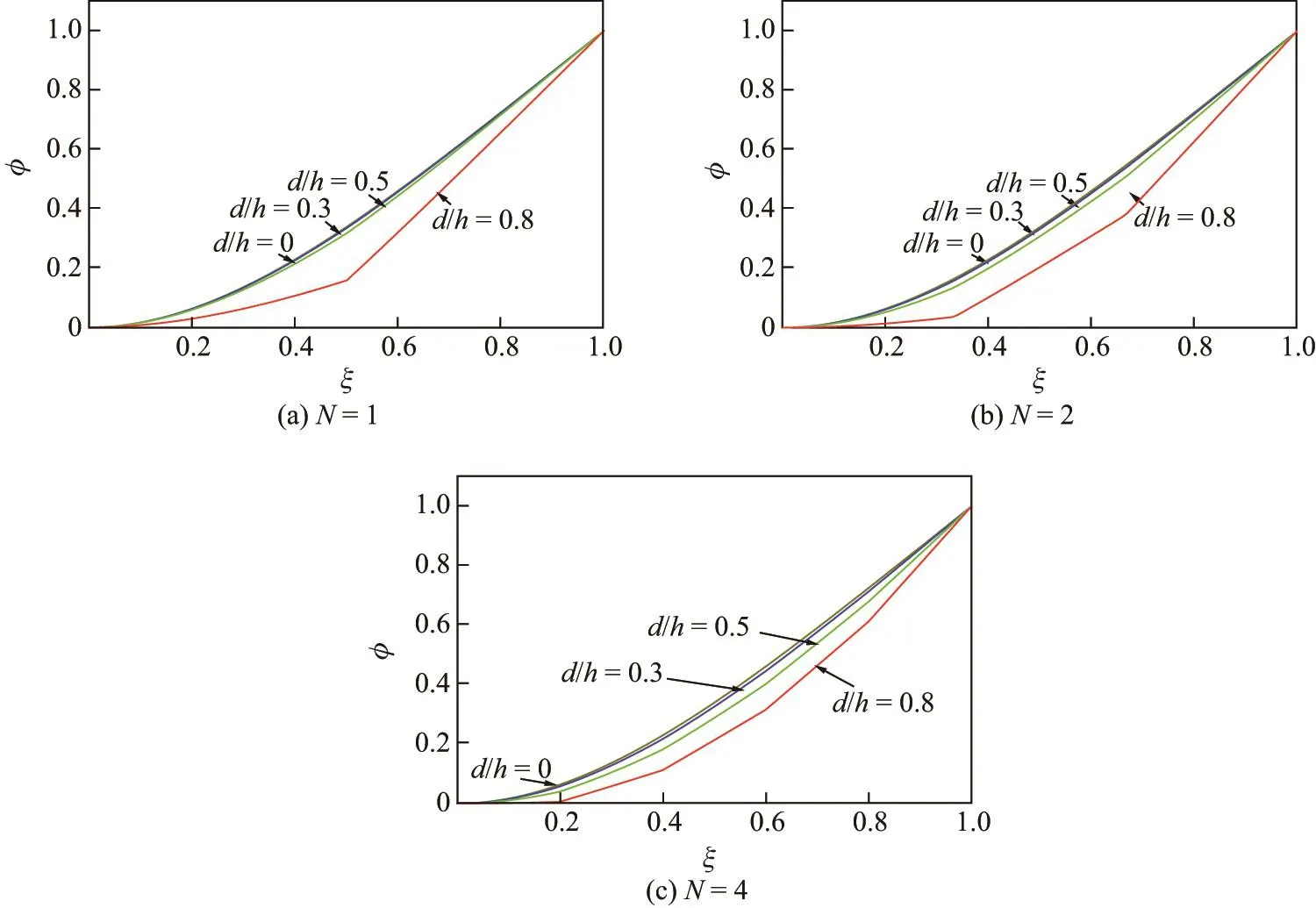
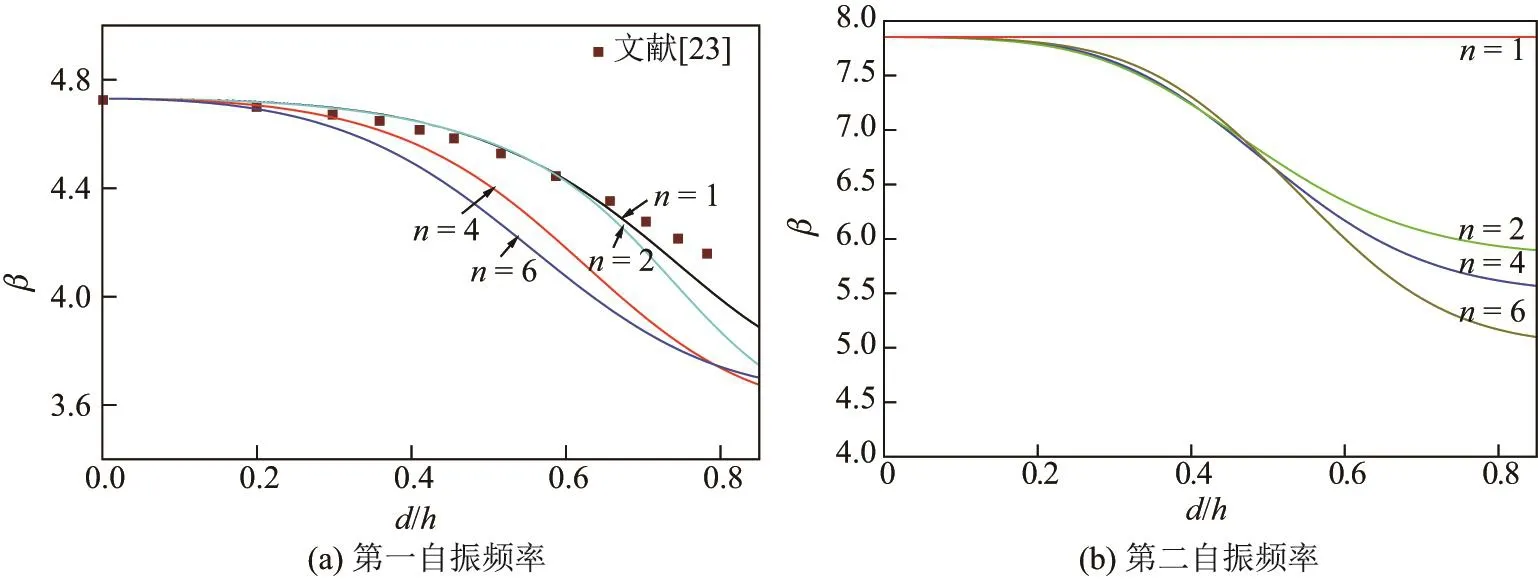
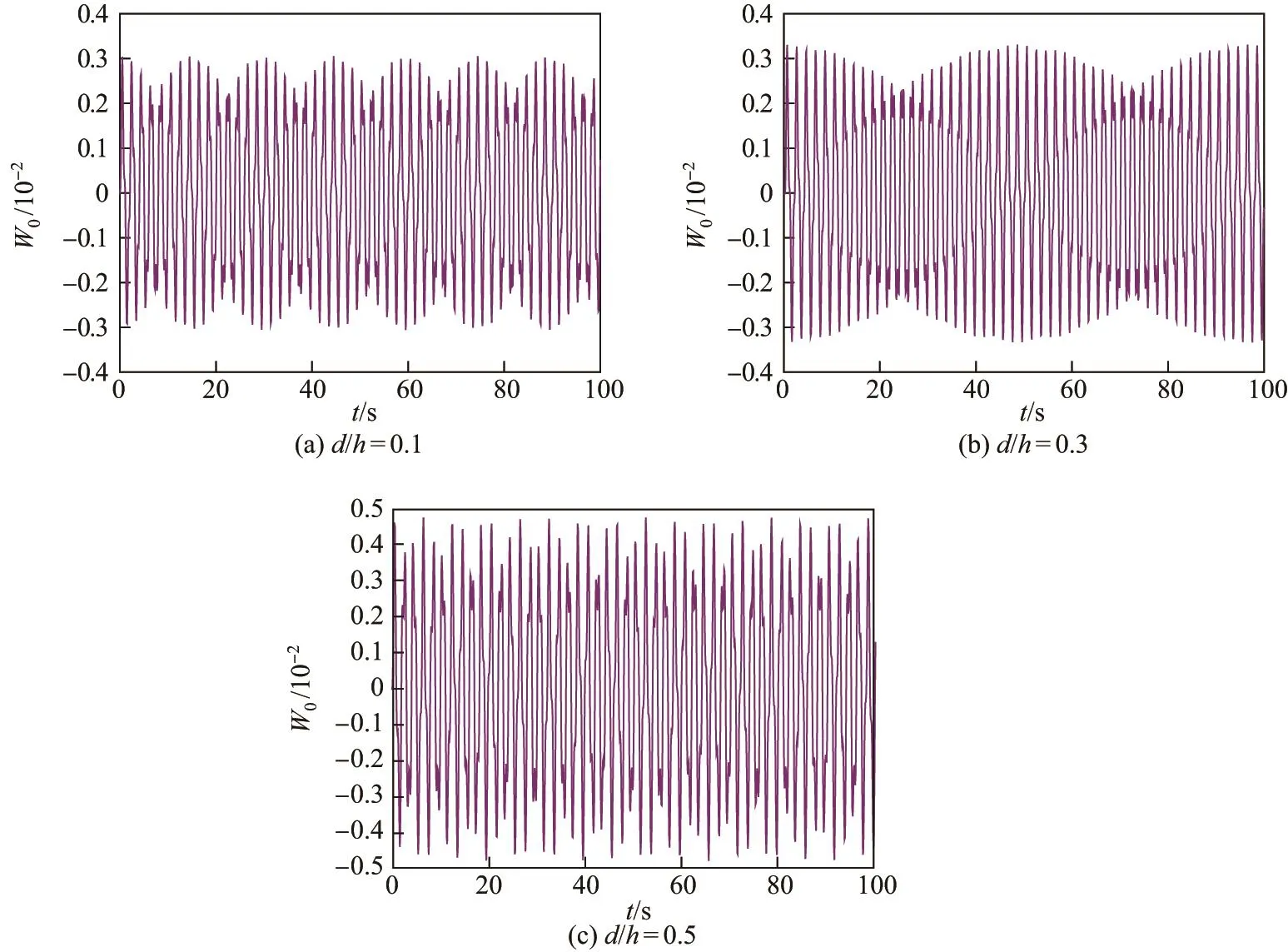
Euler-Bernoulli裂纹梁示意图如图1所示.裂纹梁的长和高分别为L和h,抗弯刚度为EI0,在x=xi(i=1,2,···,N)处存在深度为di的开裂纹,且0 式中,δ(x)为广义Delta函数. 图 1 Euler-Bernoulli裂纹梁Fig.1 Euler-Bernoulli cracked beam 记裂纹Euler-Bernoulli梁的弯曲挠度为w(x,t),线质量密度为m,则其无阻尼自由振动控制方程为 采用材料力学中横截面上弯矩和剪力的符号规定[1,13,17],此时裂纹梁任意横截面弯矩M和剪力FS分别为 对自由振动,利用分离变量法[7,15,21],可得 式中,ω为裂纹梁的自振频率,α0为相位角,ϕ(x)为对应的模态. 引入如下无量纲量和参数 可由式(2)推得裂纹Euler-Bernoulli梁无量纲自由振动控制方程 式中,β为由自振频率ω确定的特征参数,且 由式(4)可得裂纹梁任意横截面上的无量纲弯矩为 对式(6)两边积分2次,可得 式中,D1和D2为待定系数,且 令 则式(9)可表示为 利用Laplace变换及其逆变换,方程式(12)的解可表示为 式中,Ci(i=1,2,3,4)为待定系数. 从而,由式(11)可得 式中, 当裂纹不存在(ki→∞,i=1,2,···,N)时,式(14)退化无裂纹Euler-Bernoulli梁的振动模态,即 由式(14)可求得裂纹梁横截面上无量纲弯矩的振幅为 由此得 式中, 梁横截面转角的振幅为 通常,可利用梁的4个边界条件,得到待定系数Ci(i=1,2,3,4)满足的线性方程 系数矩阵A的行列式为0,即G(β)=det A(β)=0,给出确定裂纹梁自振频率的特征方程. 由于裂纹梁的模态满足正交性[24-25],在得到裂纹梁自振频率(i=1,2,···)和模态(i=1,2,···)后,可运用模态叠加法进行其动力响应分析.引入裂纹梁的无量纲横向载荷=q(x,t)L3/(EI)0,则横向载荷Q(ξ,t)作用下裂纹梁的无阻尼动力控制方程为 式中, 利用初始条件求解方程式(26)可得裂纹梁的动力响应. 考虑具有N条裂纹的简支梁,且裂纹为等间距分布.由简支梁的边界条件可得了φ(0)=0,mb(0)=0,φ(1)=0,mb(1)=0.此时,特征方程式变为 求解特征方程式(28)可得简支裂纹梁的自振频率,取L/h=20,图2给出了当裂纹深度相同(di=d,i=1,2,···,N)时,梁中等间距分布不同裂纹数N的简支裂纹梁自振频率参数β随无量纲裂纹深度d/h的变化.文献[22]采用能量法计算了不同裂纹深度下,具有跨中裂纹简支梁的自振频率,该简支梁的几何及材料参数如下:梁长L=200 mm,梁截面尺寸b×h为10 mm×10 mm,材料密度ρ=7 850 kg/m3,弹性模量E=200 GPa.以裂纹深度d/h=0.3为例,文献[22]中裂纹梁的自振频率为ω0.3=136.290 Hz,代入式(7)第一式,可得β0.3=3.058 3,与采用本工作中的方法所得结果β=3.091 0较为接近,证明了本工作中方法的正确性和有效性.由图2可以看出,随着裂纹深度d/h和裂纹数N的增加,简支裂纹梁的第一和二自振频率参数β减小;当裂纹深度d/h较小时,裂纹深度d/h对自振频率参数β的影响较小,而当裂纹深度d/h较大时,裂纹深度d/h对自振频率参数β的影响明显;裂纹数N对第二自振频率参数β的影响较第一自振频率参数β的影响更为显著.当简支梁只有一条跨中裂纹(N=1)时,第二自振频率参数β不依赖于裂纹深度d/h,其原因是此时裂纹梁第二振动模态为反对称的,其跨中弯矩为0,裂纹等效扭转弹簧不发生作用.因此,裂纹深度对第二自振频率及其振动模态无影响. 图2裂纹数N不同时简支裂纹梁自振频率参数β随裂纹深度d/h的变化Fig.2 Variation of frequency parameterβvs.crack depth d/h of the simply-supported cracked beam with different crack number N 图3 和图4分别给出了裂纹数N分别为1,2和4时,不同裂纹深度d/h下简支裂纹梁第一自振频率对应的归一化振动模态φ及其对应的梁截面转角.由图可见,对于简支裂纹梁,裂纹处归一化模态的斜率发生突变,即归一化模态的梁截面转角发生跳跃,且随着裂纹深度d/h增加,归一化模态曲线的光滑性减小,在裂纹处斜率突变增加,即归一化模态的梁截面转角跳跃增大. 图3 不同裂纹数N和裂纹深度d/h时,简支裂纹梁的归一化第一阶振动模态Fig.3 Normalized fundamental vibration mode of the simply-supported cracked beam with different crack number N and crack depth d/h 考虑具有N条裂纹的悬臂梁,且裂纹为等间距分布,此时边界条件为φ(0)=0,θ(0)=0, 式中, 取L/h=15,图5给出了当裂纹深度相同,梁中等间距分布不同裂纹数N时悬臂裂纹梁的第一和第二自振频率参数β随无量纲裂纹深度d/h的变化.由图可见:随着裂纹深度d/h和裂纹数N的增加,悬臂裂纹梁的第一自振频率参数β减小;当裂纹深度d/h较小时,裂纹深度d/h对自振频率参数β的影响较小;但当裂纹深度d/h较大时,裂纹深度d/h对自振频率参数β的影响明显.同时,具有2条裂纹(N=2)时悬臂梁的第二自振频率大于具有一条裂纹(N=1)时悬臂梁的第二自振频率,说明自振频率不仅受裂纹深度d/h及裂纹数N的影响,与裂纹位置也有一定关系. 图4 不同裂纹数N和裂纹深度d/h时,简支裂纹梁归一化第一阶振型的梁截面转角θFig.4 Angleθof beam cross-section of normalized fundamental mode of the simply-supported cracked beam with different crack numbers N and crack depths d/h 图5不同裂纹数N时,悬臂裂纹梁自振频率参数β随裂纹深度d/h的变化Fig.5 Variation of frequency parameterβvs.crack depth d/h of the cantilever cracked beam with different crack numbers N 图6 给出了裂纹数目N分别为1,2和4,裂纹深度d/h不同时,悬臂裂纹梁第一自振频率对应的归一化振型.由图可见,随着裂纹深度d/h的增加,振型曲线的光滑性减小,在裂纹处出现斜率突变. 图6 不同裂纹数量N和裂纹深度d/h时,悬臂裂纹梁归一化第一阶振动模态Fig.6 Normalized fundamental vibration mode of the cantilever cracked beam with different crack numbers N and crack depths d/h 考虑具有N条等间距分布裂纹的两端固支梁,边界条件为φ(0)=0,θ(0)=0,φ(1)=0,θ(1)=0.此时特征方程式(34)中的系数为 取L/h=20,图7给出了裂纹深度相同(di=d,i=1,2,···,N)时,梁中等间距分布不同裂纹数N的两端固支裂纹梁第一和第二自振频率参数β随无量纲裂纹深度d/h的变化.文献[23]采用Rayleigh-Ritz法计算了不同裂纹深度下,具有跨中裂纹简支梁的自振频率.简支梁的几何及材料参数如下:梁长L=200 mm,梁截面尺b×h为20 mm×10 mm,材料密度ρ=7 850 kg/m3,弹性模量E=200 GPa,以裂纹深度d/h=0.3为例,文献[23]中裂纹梁的自振频率为ω0.3=449.588 Hz,代入式(7)第一式,可得β0.3=4.671,而本工作所得结果β=4.696.随着裂纹深度d/h和裂纹数N的增加,固支裂纹梁的第一自振频率参数β减小;当裂纹深度d/h较小时,裂纹深度d/h对自振频率参数β的影响较小;但当裂纹深度d/h较大时,裂纹深度d/h对自振频率参数β的影响明显.自振频率不仅受裂纹深度d/h及裂纹数目N的影响,与裂纹位置也有一定关系.当裂纹深度较深时,裂纹梁的第一第二自振频率与裂纹深度关系的曲线都出现了交叉,此时裂纹位置对两端固支梁的频率影响较大.当两固支端梁只有一条跨中裂纹(N=1)时,第二自振频率参数β不依赖于裂纹深度d/h,此时,跨中弯矩为0,裂纹等效扭转弹簧不发生作用 图7 裂纹数N不同时两端固支裂纹梁自振频率参数β随裂纹深度d/h的变化Fig.7 Variation of frequency parameterβvs.crack depth d/h of the clamped-clamped cracked beam with different crack numbers N 作为裂纹梁动力响应分析模态叠加法的一个简单应用,考虑初始未变形,具有N条等间距裂纹的简支梁在跨中集中简谐载荷作用下的动力响应.此时,有Q(ξ,t)=Fδ(ξ−0.5)sinωt,在初始条件下,方程式(31)的解为 图8 简谐集中荷载作用下简支裂纹梁跨中挠度W0的动力响应Fig.8 Dynamic response of mid-span deflection W0 of simply-supported cracked beam under harmonic concentrated load 取简支梁梁长L=300 mm,梁截面尺b×h为20 mm×20 mm,所用材料的密度ρ=7 850 kg/m3,弹性模量E=200 GPa,外部激励的圆频率ω=230.1 Hz,F=0.33 kN.图9给出了简支梁跨中裂纹不同深度d/h时,无量纲跨中挠度W0(t)=W(0.5,t)随时间t的响应.可见,随着裂纹深度的增加d/h,无量纲跨中挠度W0(t)振幅增加,其原因是裂纹深度的增加导致梁整体刚度的减少,从而梁的变形增大,并且,随着裂纹深度的增加,振幅变化加剧. 本工作研究了开裂纹Euler-Bernoulli梁动力特性和动力响应的计算方法.在给出裂纹梁等效抗弯刚度的基础上,为避免变易系数法的复杂运算,建立了一种新的裂纹梁动力控制方程通解,即裂纹梁自由振动的求解方法.数值分析了简支、悬臂和两端固支裂纹梁的自振频率和振动模态,考察了裂纹数量和深度等对裂纹梁自振频率的影响;同时,利用模态叠加法计算分析了简支裂纹梁在集中简谐载荷作用下的动力响应,得到了如下结论. (1)基于开裂纹的等效弹簧模型,可以得到具有任意条裂纹的Euler-Bernoulli梁自由振动模态的统一显式表达式,该表达式自动满足裂纹处梁的连续性调节,避免了经典方法中连续性条件导致的繁杂求解过程,并且自由振动通解的求解方法避免了采用变易系数法求解的复杂运算. (2)随着裂纹深度和裂纹条数的增加,裂纹梁的自振频率减小;随着裂纹深度的增加,裂纹对自振频率的影响更为显著.同时,裂纹条数N对第二自振频率的影响较对第一自振频率的影响显著. (3)裂纹梁的模态曲线在裂纹处出现尖点,其斜率发生突变;随着裂纹深度增加,裂纹处斜率突变增加. (4)裂纹对裂纹梁模态和频率的影响依赖于裂纹位置,当裂纹处的弯矩为0时,裂纹对梁振动模态和频率没有影响. (5)由于裂纹梁模态满足正交性,因此,可采用模态叠加法分析裂纹梁的动力响应.对于具有一条跨中裂纹的简支梁,跨中集中简谐载荷作用下梁跨中挠度振幅随裂纹深度的增加而增加,且其振幅变化加剧.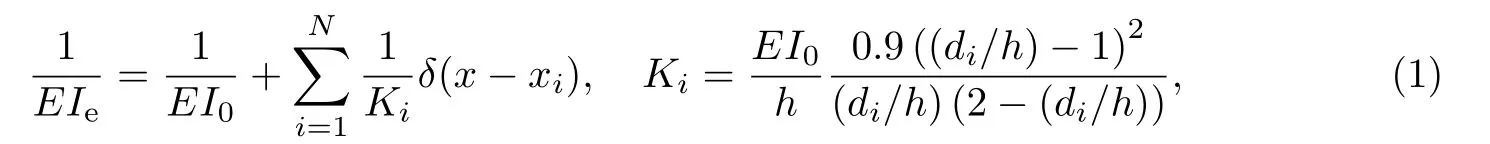
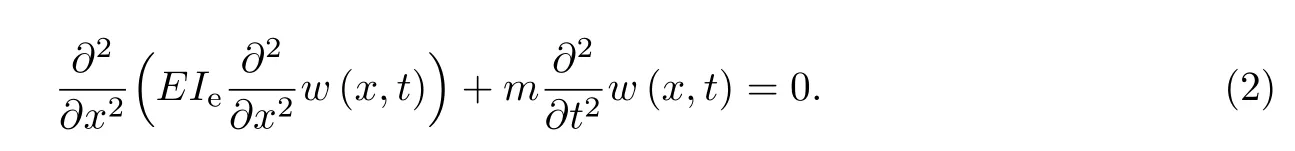
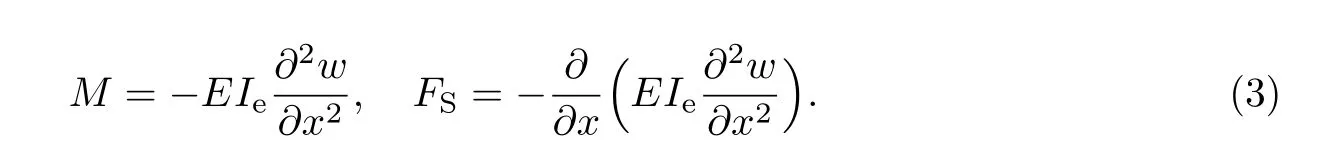
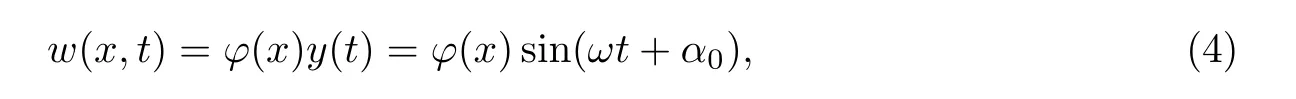
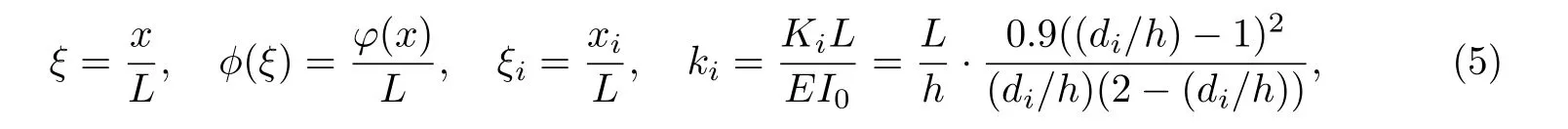
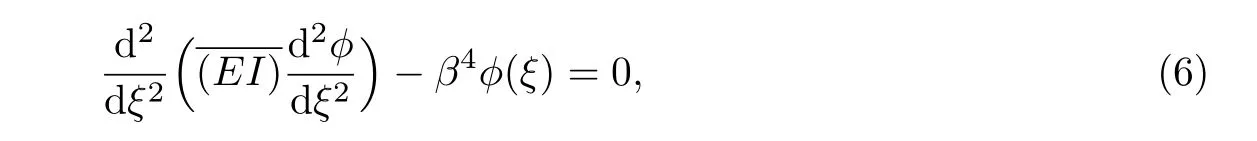
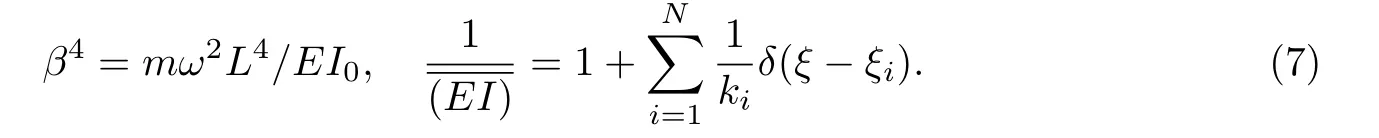
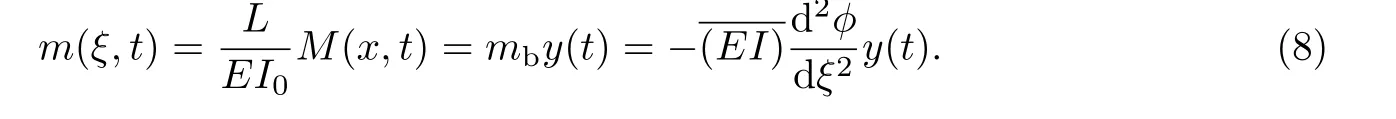
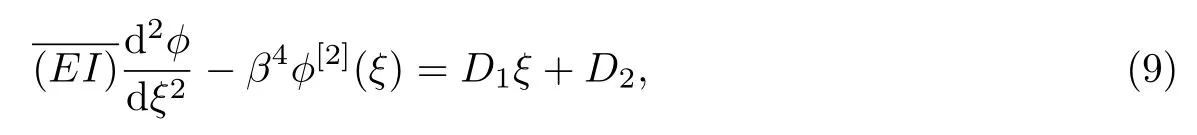
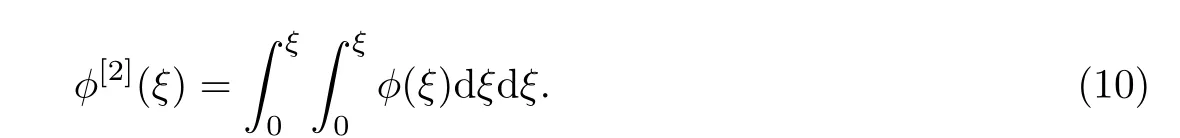
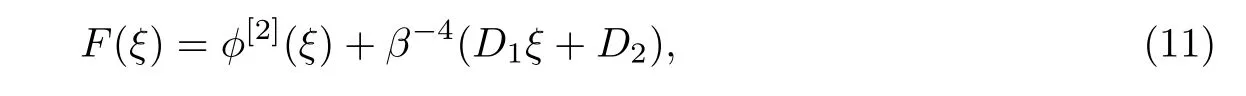

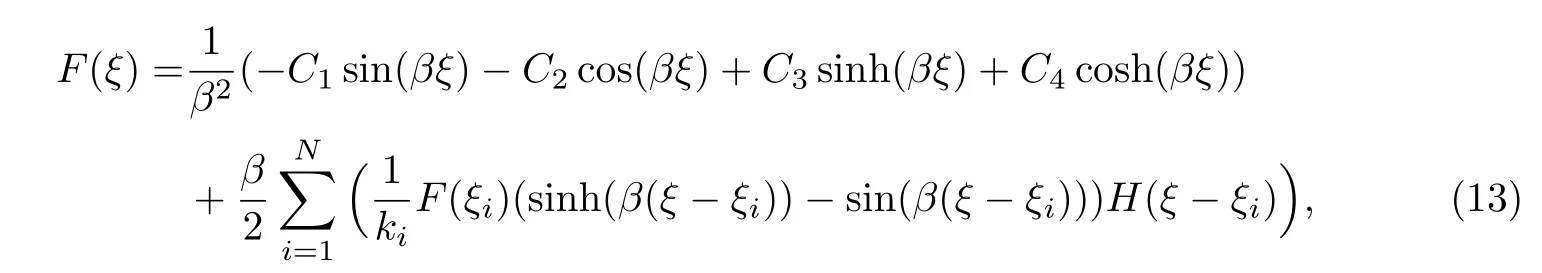
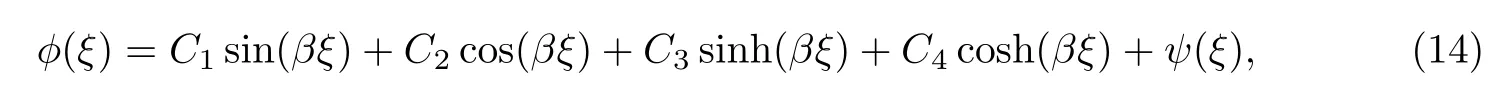
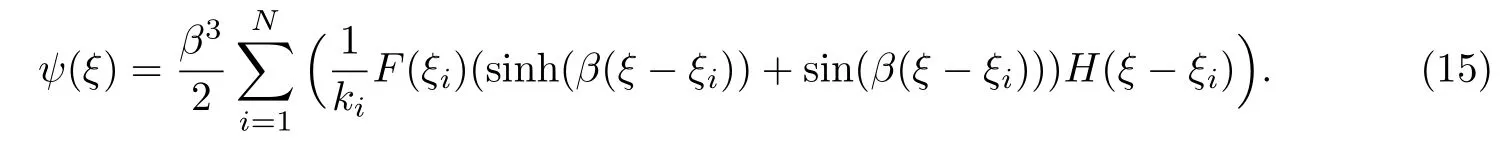
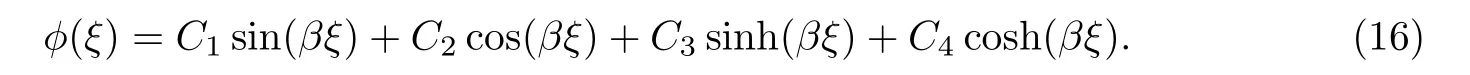
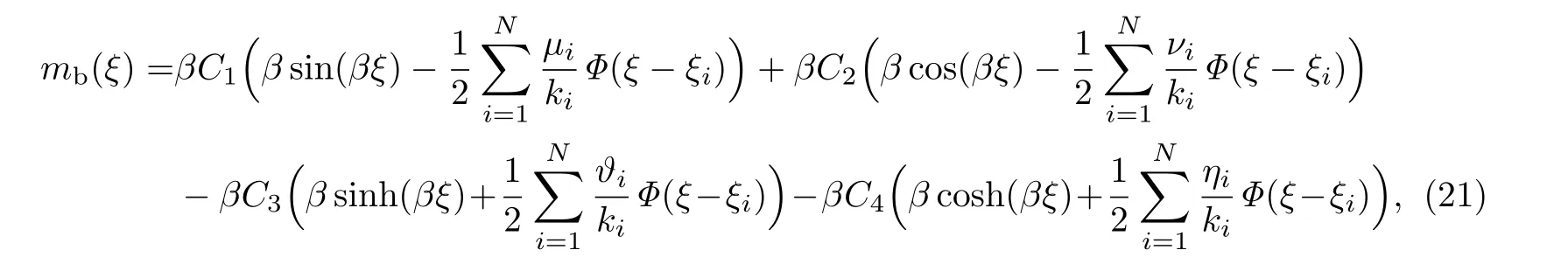
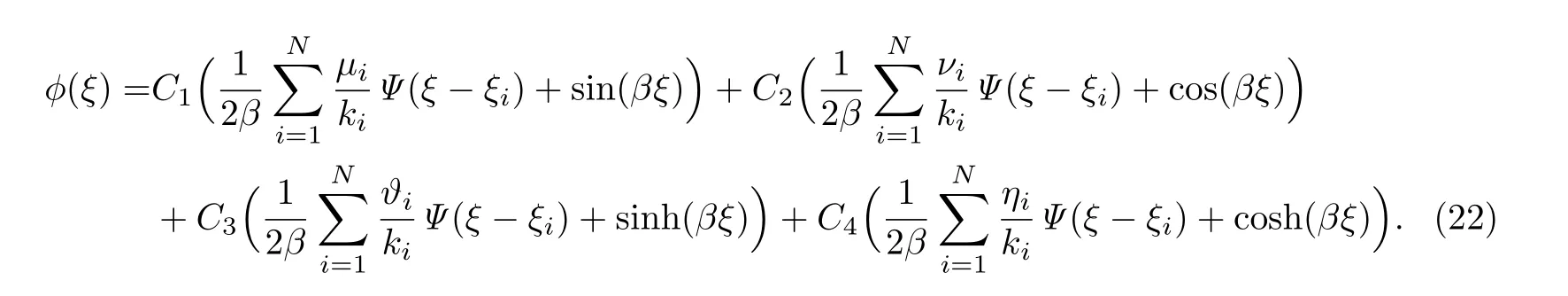
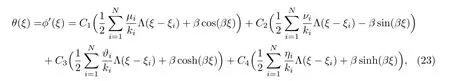

2 裂纹梁的动力响应分析
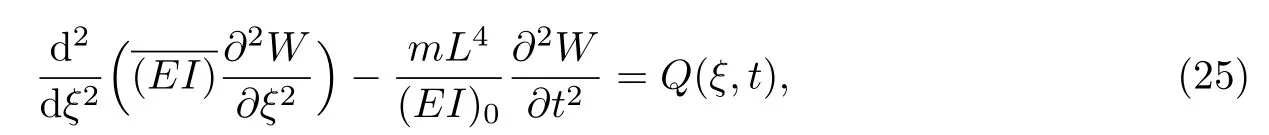
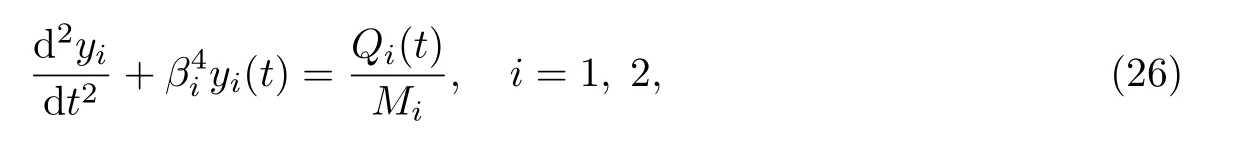
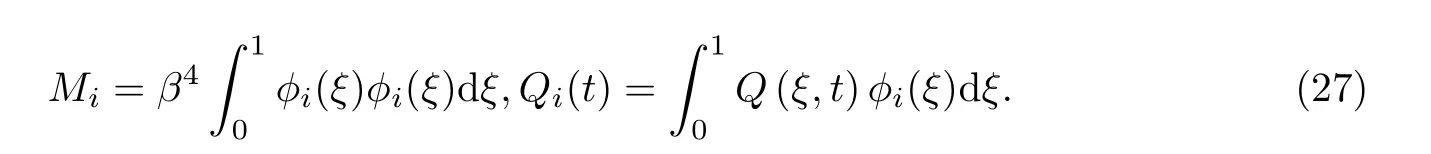
3 典型裂纹梁的自振频率
3.1 简支裂纹梁的动力特性
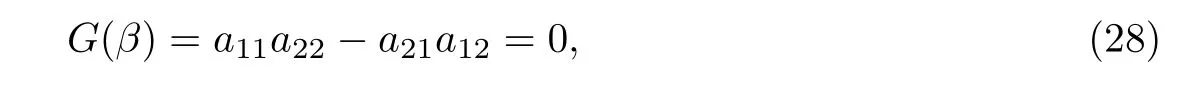
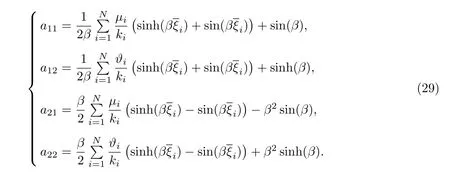
3.2 悬臂裂纹梁的动力特性
3.3 两端固支裂纹梁的动力特性
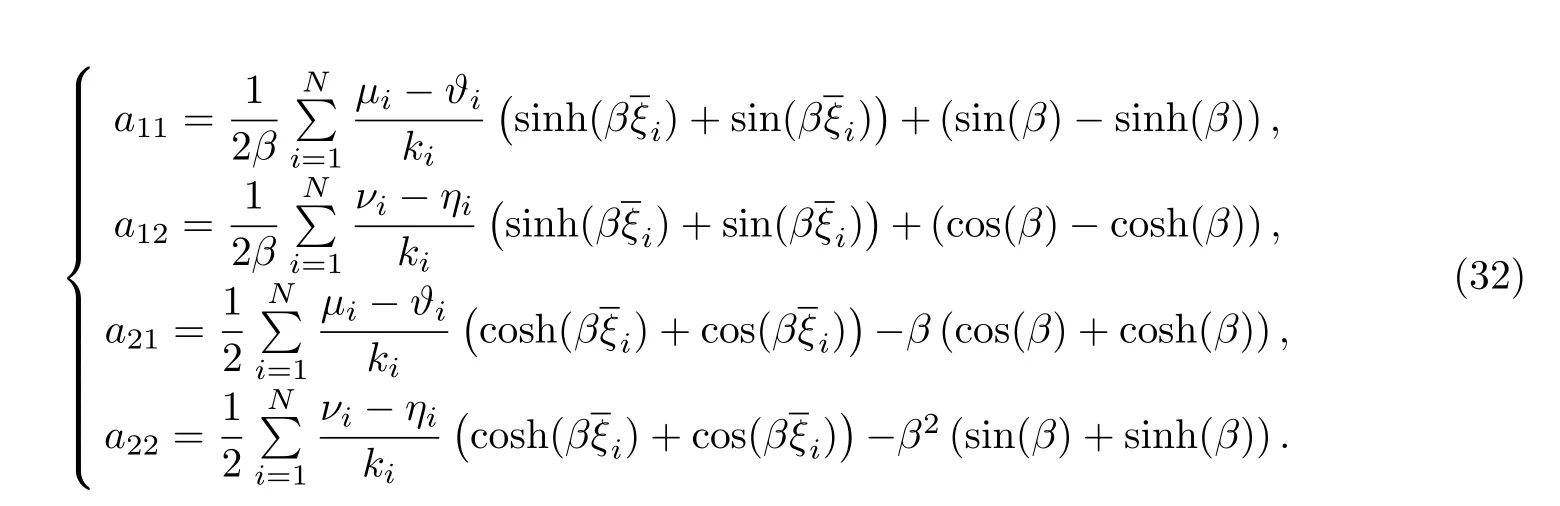
4 裂纹梁的动力响应分析
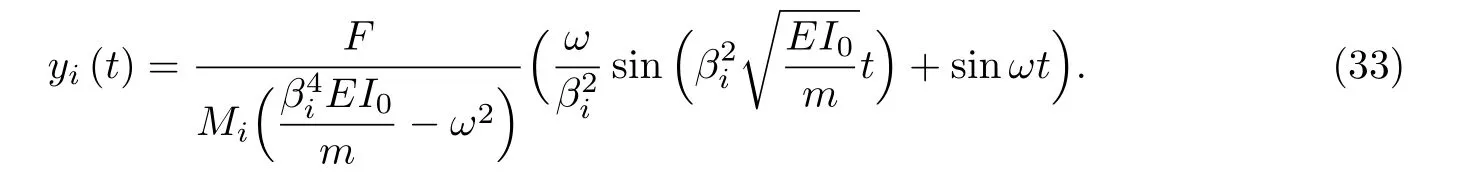
5 结束语
