欧拉方程数值求解的高精度通量分裂方法

郑秋亚，苏宁亚，梁益华

(1.长安大学 理学院，陕西 西安 710064；2.中国航空计算技术研究所 航空气动力数值模拟重点实验室，陕西 西安 710068)

0 引言

自20世纪50年代至今，计算流体力学发展出多种数值方法。优良的数值方法具备计算效率高、稳健性强、间断处分辨率高等特点(如迎风格式)。迎风格式根据网格上的信息传播方向对方程进行离散化处理，使方程所模拟的物理现象特征就与离散化方法结合起来。该格式结合物理背景得来，现今仍被广泛使用与改进。迎风格式又分为矢量通量分裂(FVS)格式[1]和通量差分分裂(FDS)格式[2]。两种格式各有优缺点：FDS格式有数值耗散小、间断分辨率和黏性分辨率高的优点，缺点是计算效率较低、稳健性较差，在高速流动情况下容易出现红斑现象[2-4]；FVS格式简单易用、计算量小，激波附近不容易发生非物理振荡，但是由于复杂度降低，导致其在间断处分辨率低，特别是遇到接触间断和剪切波时。

随后大量学者将两种格式结合起来，得到一类新的混合迎风格式，其即有FVS格式高计算效率和稳健性的优点，又保留了FDS格式的高分辨率特点。混合迎风格式有两种基本思想，第1种是对流迎风分裂(AUSM)格式[5-9]。AUSM格式根据物理现象将无黏守恒通量分裂成对流项和压力项两部分。AUSM格式中数值耗散项的系数以标量形式而不是以矩阵来计算的，这种形式在提高计算效率的同时又保留了FVS格式的简单特性。

另一种混合迎风格式是对流迎风和分压(CUSP)格式[10-11]。其中对流项的总能量为总焓的称为总焓对流迎风和分压(H-CUSP)格式[12]。另外一种主流的CUSP格式是总能对流迎风和分压(E-CUSP)格式[13-17]，其对流项的总能量是总能。

E-CUSP格式是从特征分析出发，将雅可比矩阵中的特征值u±a分裂成对流速度u和声速±a两部分，得到相应的对流项和压力项。在构造界面通量时，是将无黏通量分解为守恒型通量和压力通量，避免了矩阵运算，提高了计算效率。但是该格式对于间断处的抹平计算还是不太理想。

对于具有冲击波或接触波的问题，用本质无振荡(ENO)格式或WENO来处理是非常有成效的。其中WENO通过使用所有候选模板的凸组合来代替ENO中最平滑的模板，WENO格式比ENO格式具有更多优势。例如，模板中使用平滑的数值通量，具有更好的收敛速度，在平滑区域中接近高阶最优精度。至今为止，WENO[18-20]在对流扩散方程中特别是在双曲守恒律方程中，WENO被广泛应用。

本文的目的是在空间方向上将Zha的E-CUSP格式与WENO相耦合，来捕获间断并在平滑区域实现高阶精度，在时间方向上采用4阶总变差递减(TVD)Runge-Kutta方法[21]。本文首先推导E-CUSP格式，将其分别与3阶WENO和5阶WENO耦合(分别用WENO-3-E-CUSP、WENO-5-E-CUSP表示)。其次进行数值实验，将E-CUSP格式、WENO-3-E-CUSP格式和WENO-5-E-CUSP格式进行对比，通过数值结果分析发现，新的格式更加准确、稳健和有效，从而表明采用WENO建立的高分辨率模型可以更好地模拟激波管问题。新的格式能够保证在解的光滑区域精度更高，在解的间断区域保持陡峭的间断过渡和本质无振荡性质。最后对全文进行总结和展望。

1 数值方法

1.1 控制方程

控制方程为一维Euler方程，其守恒形式为

(1)

1.2 E-CUSP格式

利用有限体积法，对(1)式在区间单元上进行积分，可得

(2)

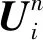
E-CUSP格式的主要思想就是将通量分解为守恒型通量和压力型通量两项。这样处理可以有效避免矩阵运算带来的时间消耗，大大减少计算量，提高计算效率。(1)式中雅克比矩阵可表示为

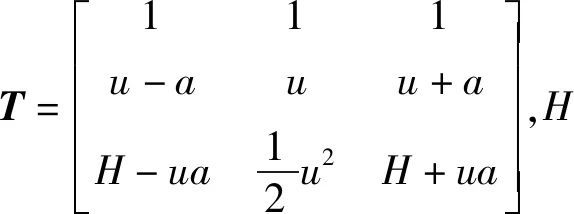
F=TΛTTU.

(3)

由(3)式可得

其中Fc表示守恒型通量，Fc=u[ρ,ρu,ρe]T;Fp表示压力型通量，Fp=[0,p,pu]T.

守恒型通量Fc可表示为

(4)

在压力型通量Fp中，动量方程中的压强p可表示为

p=P+pl+P-pr,

(5)

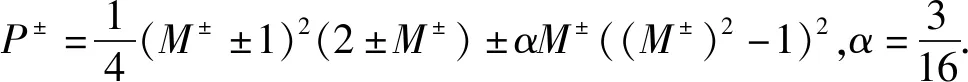
(6)

最终E-CUSP格式中的通量F可表示为

(7)

1.3 WENO格式

WENO格式用于评估变量Ul和Ur.其中变量Ul的WENO格式可以写成：

式中：s为候选模板数；qk(k=0,…,s-1)为不同模板中变量的重建；ωk为权重，

(8)

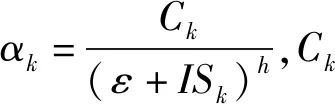
(9)

ε是为了避免分母变为0，Jiang等[20]的数值实验表明，只要ε的选择在10-5～10-7范围内，对结果的影响不大，通常ε取10-6.

变量Ur的WENO格式与Ul类似，向右移动1个空间节点即可。

对于3阶(s=2)WENO，有

对于5阶(s=3)WENO，有

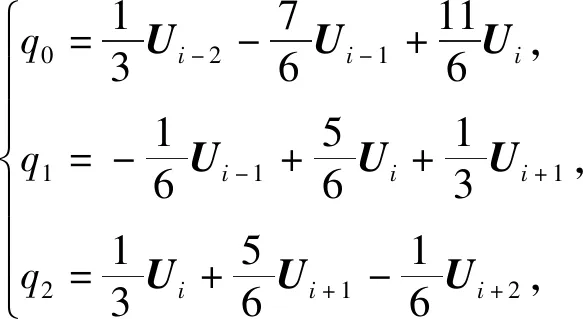
1.4 Runge-Kutta方法

2 数值实验

2.1 算例1：一维Euler方程激波管问题

一维激波管非定常流动问题中包含激波、接触间断等流动特征，在数值计算中网格容易生成，初始条件、边界条件容易处理，常被用来考察数值格式性能。

本文在区域[0,1]上求解初值问题：

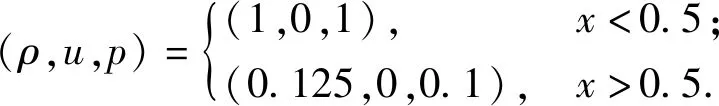
(10)

采用Neumann边界条件，取空间网格点数200个，计算中条件数CFL=0.1.

图1所示为速度、压力、马赫数和密度在t=0.25时用E-CUSP格式、WENO-3-E-CUSP格式和WENO-5-E-CUSP格式分别求解一维Euler方程激波管问题得到的无量纲化数值计算结果。从图1中可以看出，E-CUSP格式在激波和接触间断处的过渡较宽，WENO-3-E-CUSP格式和WENO-5-E-CUSP格式在接触间断和激波处的计算结果明显优于E-CUSP格式。尤其在激波处过渡带明显变窄。图1表明WENO-3-E-CUSP格式和WENO-5-E-CUSP格式的数值模拟轮廓基本相同，在激波和接触间断处WENO-5-E-CUSP格式要比WENO-3-E-CUSP格式所获结果更加接近理论解。

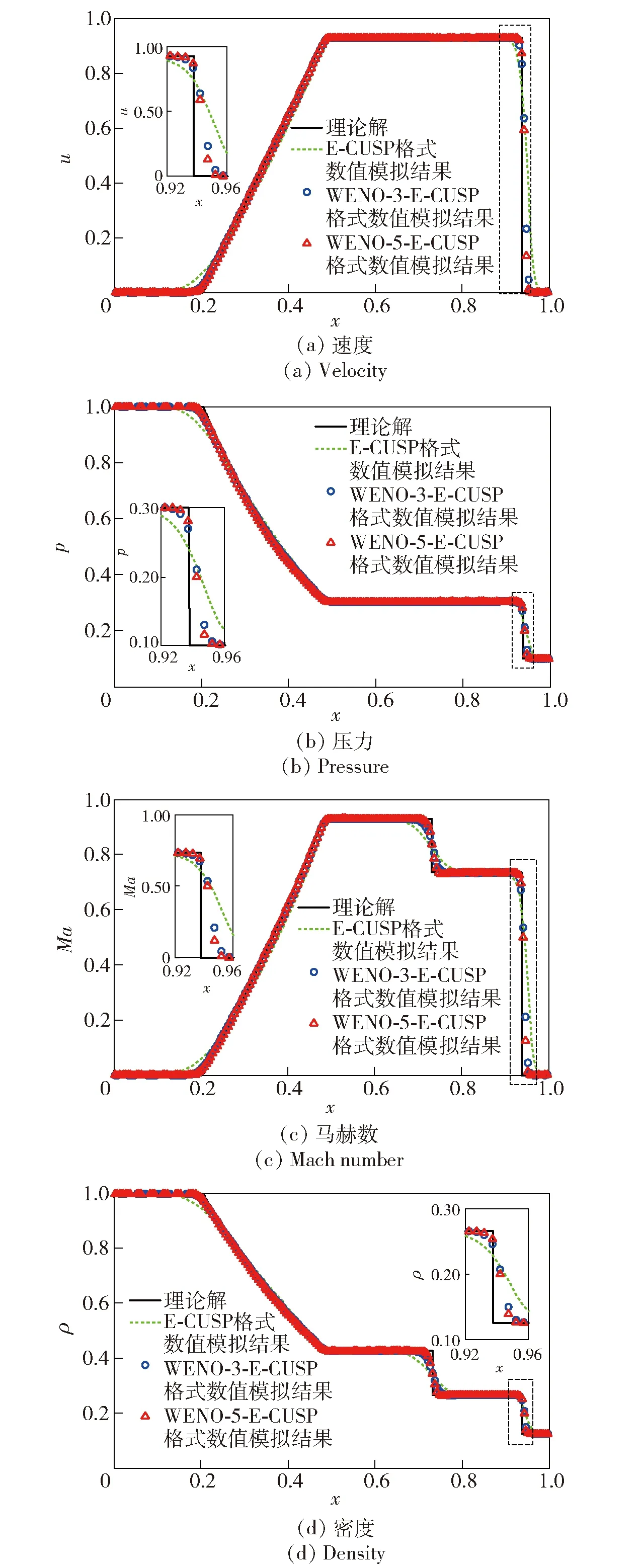
图1 一维Euler方程激波管问题的数值解Fig.1 Numerical solution of shock tube problem in one-dimensional Euler equation

2.2 算例2：一维Euler方程Lax激波管问题

在区域[0,1]上求解初值问题：

(11)

采用Neumann边界条件，取网格点数200个，计算中条件数CFL=0.03.图2所示为速度、压力、马赫数和密度在t=0.16时用E-CUSP格式、WENO-3-E-CUSP格式和WENO-5-E-CUSP格式分别计算一维Euler方程Lax激波管问题的无量纲化后的数值模拟结果。

图2 一维Euler方程Lax激波管问题的数值解Fig.2 Numerical solution of the Lax shock tube problem in one-dimensional Euler equation

该问题的理论解由稀疏波、接触间断和激波3个波构成。从图2的局部放大图中，可以观察到WENO-3-E-CUSP格式和WENO-5-E-CUSP格式在接触间断和激波处的计算结果依旧明显优于E-CUSP格式，并且WENO-5-E-CUSP格式比WENO-3-E-CUSP格式所获结果更加接近理论解，与算例1观察到的结果相同，表明新的格式对解的捕捉更加精准。比较图1和图2可以看出，算例2中稀疏波的波尾部和激波的顶部有过冲现象。算例2的稀疏波与接触间断之间过渡带较宽且出现明显的振荡。图3所示为算例2中压力的局部放大图。

图3 算例2压力局部放大图Fig.3 Partial enlarged detail of pressure in Example 2

由于E-CUSP格式的守恒变量经过WENO的重构，使得其计算量大大增加。表1展示了3种格式在算例1和算例2所用的时间，对比可发现新格式的计算效率较低、时间代价大。WENO-3-E-CUSP格式和WENO-5-E-CUSP格式的计算时间基本相同。算例2中，WENO-5-E-CUSP格式所用的计算时间甚至比WENO-3-E-CUSP格式要少。综合以上分析可知，采用WENO-5与E-CUSP进行耦合是最佳的选择。

表1 不同数值格式的CPU计算时间Tab.1 CPU computing times of different schemes s

3 结论

本文通过数值模拟一维Euler方程组，以相应的Riemann问题解为基础，考察了低耗散E-CUSP格式耦合高精度WENO格式后的性能。算例结果表明，由于WENO的重构使得计算量大大增加，新格式的计算效率相比E-CUSP格式的计算效率较低。在较大时间代价的情况下，新格式对接触间断和激波的捕捉能力较强，尤其是对激波的捕捉能力仅需要3～4个网格单元。采用WENO-5耦合E-CUSP格式是最佳的选择，实验结果表明新的格式有更高的准确性和稳健性。

本文主要针对欧拉方程进行数值模拟，来验证新格式的优势。对计算流体力学中的实际问题，如磁流体动力学[22]、机翼展开[23]和空泡流动[24]等问题，应用新格式进行数值模拟将会产生更好的预期结果。将精度更高的WENO[25-26]与E-CUSP格式耦合，并结合自适应算法来提高计算效率，是进一步研究的方向。