基于低能电子束的绝缘物- 半导体样品放电特性研究

霍志胜，蒲红斌，余宁梅，李维勤

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

0 引言

电子束辐照技术是微电子器件检测、加工的重要手段[1]。在微电子器件检测中，起因于电子束辐照产生的带电效应一方面可用于基于扫描电镜的内部结构检测，另一方面带电效应影响其成像和检测的准确性[2-5]。在微纳器件加工中，电子束曝光引起的电荷沉积会影响微细加工的精度和可靠性[6]。此外，在航天器件领域，研究器件的放电特性对于提高器件的抗辐照能力具有非常重要的意义[5]。

绝缘物- 半导体结构常见于微电子器件，当入射能量大于第2临界能量(电子产额等于1)的电子束辐照绝缘物- 半导体样品时，会在样品表面、近表面产生明显的荷电现象，沉积电荷产生的表面电场和内部电场会影响出射电子的轨迹，从而影响检测、加工的性能[7-9]。然而，这些电荷会在样品近表面和内部沉积较长时间，且难以被完全消除。

为了消除、降低这种残留电荷对器件的不利影响，研究人员开展了相关研究[10-12]。一种有效方法是给样品辐照入射能量处于第1临界能量和第2临界能量之间的低能电子束，使样品正带电，从而中和样品的负电荷，达到消除样品带电的目的。其关键问题是确定入射电子束的能量、束流及辐照时间，核心物理问题是样品内部电荷放电、中和过程的动态变化特性。要实现样品内部负电荷的中和，必须定量了解其内部电荷分布，但样品内部负电荷分布受散射和输运过程的综合影响，分布较为复杂且动态变化。更重要的是，当采用低能电子束中和样品内部负电荷时，入射的中和电子束既受表面势垒影响又受样品内部负电荷产生的静电场影响。因此，实验方法无法从机理上揭示样品放电及中和特性的瞬态演变特性。

数值方法是研究电介质样品放电和中和特性的有效方法[13-16]。本文研究基于使样品正带电的低能电子束辐照绝缘物- 半导体结构样品放电特性及中和机理。首先介绍放电特性数值计算模型及实验平台；然后给出自然条件下样品内放电特性；最后分析采用低能电子束辐照的放电驰豫特性，阐明提高放电效率的最佳辐照条件。

1 数值模型

本文针对常见的入射能量大于第2临界能量的绝缘物- 半导体样品负带电的放电及中和特性开展研究，即在负带电过程达到平衡后分析其自然条件下的放电机理，并研究使样品正带电的低能电子束辐照下的放电及中和机理。

入射电子束辐照样品后，首先与样品发生散射过程，产生大量电子空穴对。激发的电子经历复杂的输运过程。

1.1 电子散射过程

电子束照射样品产生带电的首要过程是电子束与样品的弹性和非弹性散射。弹性散射不损失能量，对于能量低于10 keV的情况，采用Mott散射模型计算其微分截面[15-16]：

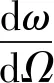
(1)

式中：ω为散射截面(cm2/atom)；Ω为立体角(°)；θ为散射角(°)，是前后两次散射方向之间的夹角；f(θ)和g(θ)为分波散射振幅,可通过分波法求得。对微分散射截面积分，可得到总的散射总截面σt为

(2)

由σt可得到弹性散射平均自由程为

(3)

式中：A为分子量；Na为Avogadro常数；ρ为样品密度。

非弹性散射会损失能量、激发出次级电子，并在碰撞位置留下1个带正电的空穴。由于入射能量较低，采用Penn介电模型模拟入射电子的非弹性散射过程，假设入射能量为E，入射电子的自由程λi满足[17]:

(4)

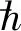
上述弹性和非弹性散射过程可采用蒙特卡洛方法来实现[15]。

1.2 俘获与复合过程

Poole-Frenkel俘获截面模型是目前描述电子动态俘获过程的有效方法，其电子密度n(t)随时间t的变化[18]可写为

(5)

式中：Nt为陷阱密度；Q(t)为俘获电子密度；Sp为修正的俘获系数；对于石英样品，ε=3.9μ0，μ0为真空介电常数。

此外，一些电子空穴对会以一定概率复合。电介质样品中电子和空穴的复合机理比较复杂，一般认为复合包括直接复合和间接复合两种类型。直接复合是由电子在导带和价带之间的直接跃迁形成的。为了简化计算，本文的研究仅考虑直接复合。

1.3 电荷漂移过程

样品内部未被俘获的电子和空穴(正电荷)在内建电场和密度梯度作用下会发生漂移[16,19]。假设样品台为Oxy平面，电子束入射方向为z轴，电荷的漂移过程满足如下电流连续性方程：

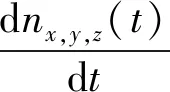
(6)

(7)

式中：nx,y,z(t)为t时刻电子密度；Jx,y,z(t)为t时刻电子电流密度；q为电子电量；Vx,y,z(t)为空间电位；μ和D分别为电子迁移率和扩散系数。

1.4 电位计算

样品内非界面处的电位根据计算区域内每个网格点的电荷密度，由如下泊松方程获得：

(8)

式中：p(t)为空穴密度。

上述方程(6)式～(8)式采用有限差分法求解。

对于真空- 介质- 半导体结构，镜像法是求解其空间电位的一种间接方法[12]。应用镜像法时，用闭合边界外虚设的电荷分布，代替实际边界上复杂的电荷分布进行计算。图1所示为半导体上覆盖厚度为l、介电常数为ε1电介质时的简化情况，图中z表示径向电荷放置点与分界面的距离。设定介质表面与真空分界面处为z=0，空间电荷位于介质内，与表面距离为d，其位置坐标为(x0,y0,0)。在系统中存在真空- 介质以及介质- 半导体2个媒质的分界面，即存在2个镜像的镜面。在求解介质样品内和真空中的电位时，镜像电荷的位置和大小分别如图1和图2所示。图2中ε2为绝缘样品介电常数；β=2ε0/(ε1+ε0)，ε0为真空介电常数。

图1 介质样品内部镜像电荷的位置和大小Fig.1 Location and size of image charge in dielectric sample

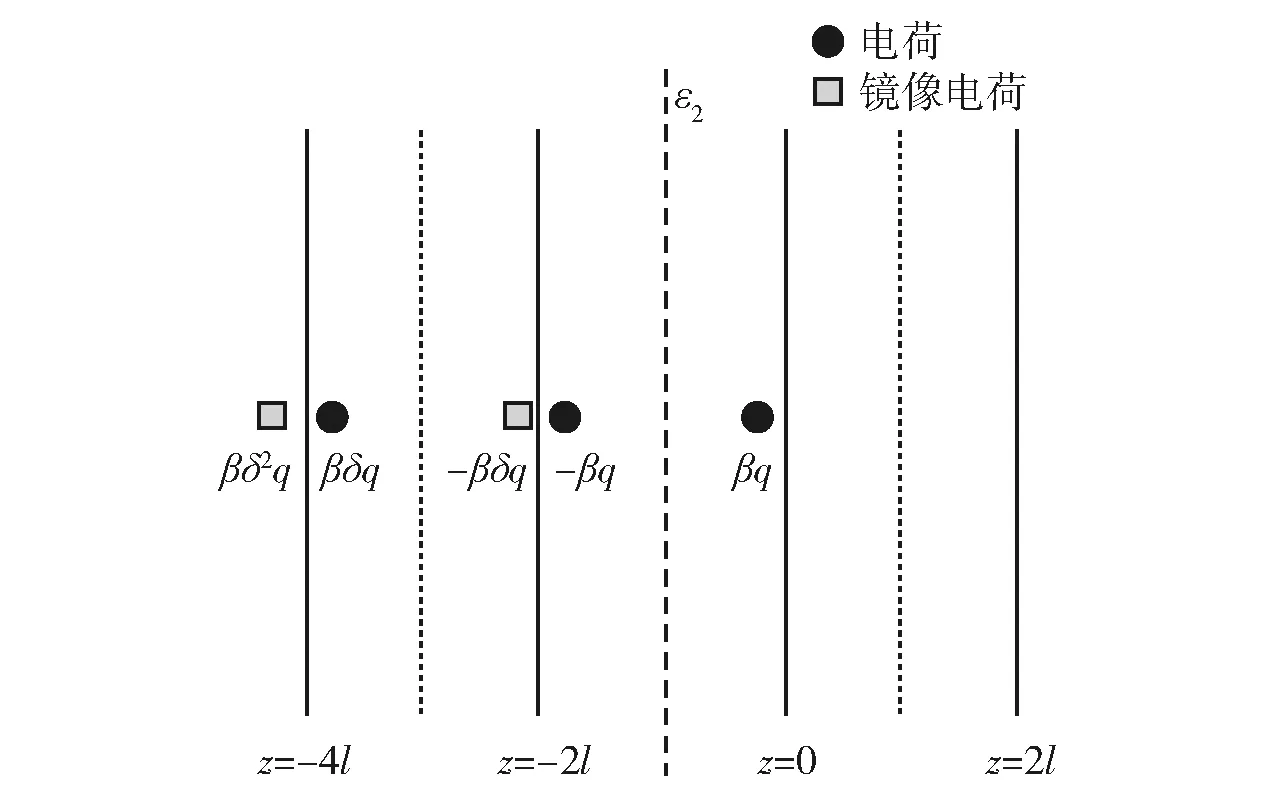
图2 真空中镜像电荷的位置和大小Fig.2 Location and size of image charge in vacuum

根据图1和图2所示镜像电荷的位置和大小，可以分别求得介质样品内电位V1和真空中电位V0.样品内-l≤z≤0，有

(9)

(10)

2 实验

图3所示为本文采用的实验装置简化示意图。电子枪发射电子束垂直照射到样品表面，样品下方为接地的金属支架，样品台偏压为-20～20 V可调。样品台上方为二次电子收集器，并通过开关K来控制背散射电子接收与否。在样品侧上方放置开尔文探针，用于测量样品表面电位。实验中钨灯丝电子枪的束斑为100 nm，电子束能量可在1～10 keV范围内调整，束流可在1～100 nA范围内调整。

图3 实验装置示意图Fig.3 Schematic diagram of experimental platform

3 结果及分析

以SiO2-Si样品作为研究对象，样品参数设置如表1所示。

表1 样品参数设置Tab.1 Samle parameter settings

本文研究在较高能量电子束辐照使样品负带电并达到平衡后，其放电机理以及样品在正带电的低能电子束辐照下的带电中和机理。

3.1 电子产额及空间电荷分布

电子总额是影响电介质样品正负带电的主要因素。首先，采用脉冲电子束辐照方式分析样品的电子产额，这里，电子束宽度为100 nm，时间间隔为10 s.在脉冲电子束辐照下，样品的带电非常微弱[13]。

图4给出了样品在不同入射能量Eb下电子总产额σ的模拟和实验结果。其中实验结果是9次测量的统计结果。从图4中可看出：当Eb>3 keV时，由于电子总产额小于1，样品负带电；当入射能量小于3 keV且大于第1临界能量时，样品正带电。因此，首先假定入射能量为4 keV的电子束长时间辐照样品，然后分析其负带电的自然放电驰豫特性，最后采用使样品正带电的能量为2 keV的电子束辐照样品，分析其放电机理及其时变特性。

图4 电子总产额的模拟和测量结果Fig.4 Simulated and experimental results of electron yield

图5给出了空间电荷密度S(t)在样品内部沿入射方向的模拟结果。照射条件为束能为4 keV，束流为1.6 nA.从图5中可以看出，在样品近表面约0.5 μm上方空间电荷为正，而在其下方为负。其原因如下：当入射电子束能量为4 keV时，电子总产额小于1(见图4)，在样品表面及近表面通过非弹性散射激发的电子从表面出射，留下带正电的空穴。而在样品内部，激发的电子在浓度梯度作用下向0电位的衬底输运，其中部分电子会被样品的体缺陷俘获，因此由多余电子组成的负空间电荷分布在该区域，进一步阻碍电子向下输运。在样品更深处，由于电子迁移率较低，电子很难输运到此处，空间电荷密度逐渐降低并趋于0.

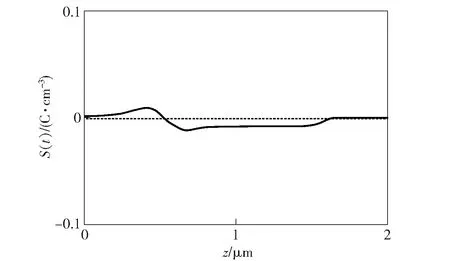
图5 空间电荷密度沿入射方向分布Fig.5 Simulated space charges in the irradiation direction

图6所示为长时间辐照下空间电位V(t)沿入射方向的分布。从图6中可以发现：沿入射方向，在约0.6 μm上方，空间电位保持微弱的减小趋势；而在其下方，空间电荷逐渐上升至0电位。这是因为虽然样品整体负带电其空间电位整体为负，但是在近表面二次电子的出射导致该区域空间电位较高；而在样品内部，沉积负电荷密度逐渐减少，使得空间电位逐渐升高并趋于0电位。最后，虽然入射电子束仅为4 keV，但样品表面电位依然低至约-0.89 kV，这种强负带电会影响器件的后续加工及检测。

图6 空间电位沿入射方向分布Fig.6 Simulated space potentials in the irradiation direction

3.2 放电特性

下面分析自然放电条件下的表面电位特性。图7所示为电子束停止辐照后表面电位Vs的时变特性。从图7中可以看出，长时间放置下，表面电位逐渐升高，样品的负带电强度将逐渐减弱，但是并不会消除，表面电位依然可以达到约-25 V.这种带电强度依然会影响后续的加工、观测和检测。

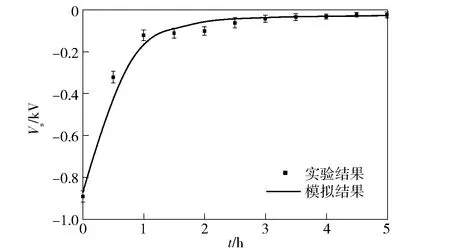
图7 放电条件下表面电位Vs的时变特性Fig.7 Vs as a function of irradiation time under discharge conditions

3.3 带电中和特性

图8所示为能量为2 keV低能电子束辐照下电子总产额σ的演变特性，其中方框和虚线分别为σ的实验和模拟结果。从图8中可以看出，σ从辐照初期的2.8逐渐减小，并最终趋于1个接近于1的稳定值。由于初始表面电位为-0.89 kV，当2 keV低能电子束辐照时，其实际入射能量为1.1 kV，因此σ的初始值为1.1 kV所对应的2.8，而不是0初始表面电位的1.5(见图4)。

随着电子束辐照增加，σ逐渐下降并趋于1个稳定值。事实上，在正带电条件下，随着电子束的持续辐照，由于σ>1，样品近表面正空间电荷量逐渐增大，样品内部原本沉积的负电荷逐渐减小，并最终趋向于0电位。此时，可停止低能电子束的辐照，表明负电荷中和过程完毕。

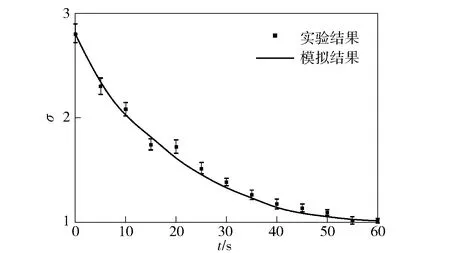
图8 电子总产额σ的瞬态特性Fig.8 σ as a function of irradiation time

图9给出了表面电位Vs的演变特性，从中可以发现Vs从辐照前约-0.89 kV逐渐上升，并逐渐趋于一个接近于0的稳定值。事实上，在正带电条件下，随着电子束辐照的增加，由于σ大于1，样品近表面正空间电荷量逐渐增大，Vs将逐渐升高。随着表面电位逐渐升高，σ逐渐降低，最终表面电位将趋近于0，此时整个样品的带电逐渐减弱。

图9 表面电位Vs的瞬态特性Fig.9 Vs as a function of irradiation time

最后分析中和过程完成后继续电子束照射时的放电瞬态特性。事实上，中和过程完成后样品表面电位达到0电位时，如果继续电子束照射，则由于电子产额大于1，样品内部将沉积正电荷，样品表面将为正电位。正表面电位会吸引入射电子照射表面，增加了电子束的着陆能量并降低了电子总产额，反过来又降低了表面正电位。最终整个样品的带电又会达到新的平衡状态。

3.4 参数对中和特性的影响

图10所示为束流为1.6 nA时，不同电子束能量Eb下从开始辐照到表面电位为0时的暂态时间。从图10中可以看出，随着Eb的增大，暂态时间先下降至1个极小值(对应入射能量为1.5 keV)，然后逐渐增大。事实上，由于表面电位为-0.89 kV，能量为1.5 keV时的入射电子着陆能量为600 eV，正好对应电子产额最大值时的入射能量600 eV(见图4)。这里，着陆能量越接近600 eV，电子产额越大，样品内部沉积的正电荷越多，因此其暂态过程更快达到放电平衡。

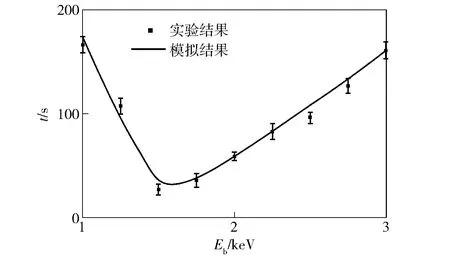
图10 暂态时间随入射能量的变化特性Fig.10 Transient time vs.incident energy

图11所示为电子束能量为2 keV时，不同束流Ib下从开始辐照到表面电位为0时的暂态时间。从图11中可以看出，随着束流的增大，暂态时间变小。这是因为随着束流的增大，单位时间内的入射和出射电子数量增大，因此样品内部沉积更多正电荷，放电过程更快达到平衡。

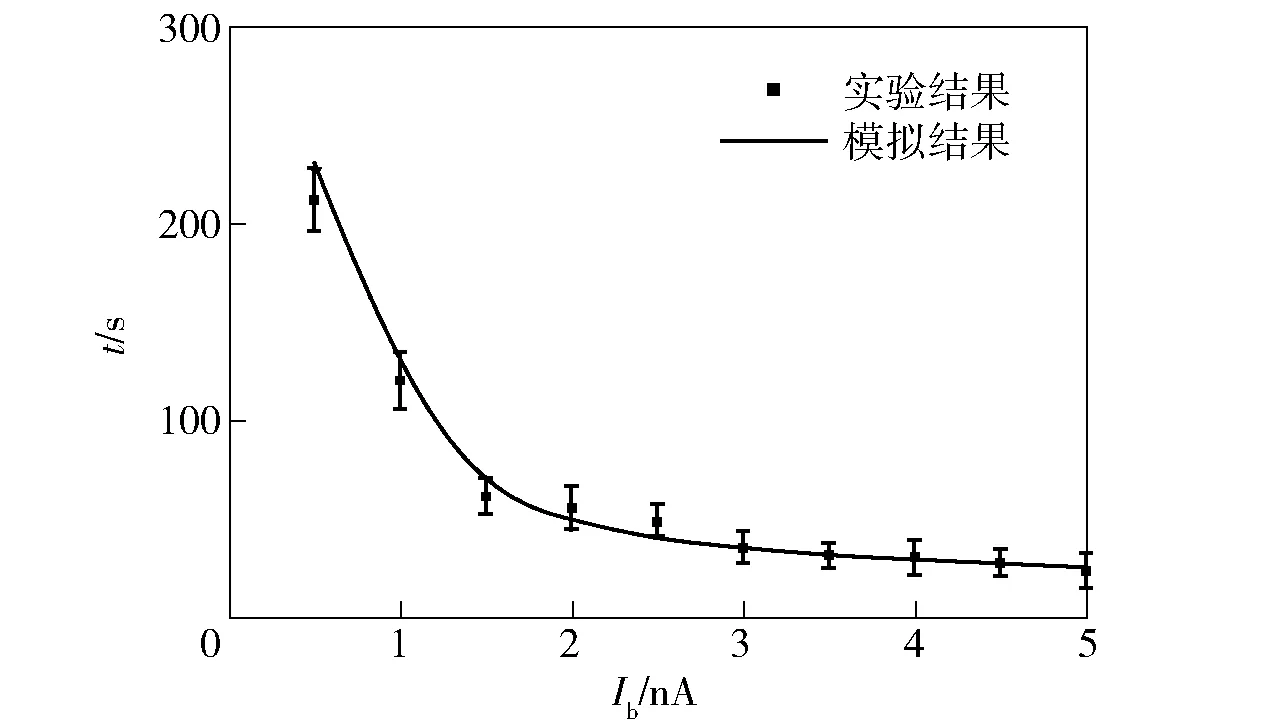
图11 暂态时间随束流的变化特性Fig.11 Transient time vs.beam current

需要指出的是，本文放电过程的平衡是基于表面电位是否为0来判定的。事实上，由于电子束能量的高低会影响电子的入射深度，即使表面为0电位，样品内部仍然可能沉积负电荷。但随着辐照时间的延长，由于内部电子的漂移、扩散以及陷阱的去俘获效应，正负电荷会逐渐抵消，其带电强度将进一步减小。

受加工条件的影响，样品相关参数例如电子迁移率、陷阱密度等取决于样品的物理结构特性、生长条件等，这些参数的取值会影响样品的放电瞬态过程。因此，相关计算结果可能会有差异，从而导致实际测量结果与计算值之间有偏差，但相关的计算结果及分析不会影响绝缘物- 半导体结构样品的放电及中和的物理本质。

4 结论

本文以SiO2-Si结构样品为例，研究了绝缘物- 半导体结构样品的放电驰豫特性，以及基于低能电子束的带电中和机理。得到主要结论如下：

1)在较高能量电子束辐照下，样品内部呈现明显的负带电特性；在长时间放置下，在样品内部电荷漂移、复合作用下，样品的负带电强度逐渐减弱，但不会彻底消除。

2)在低于第2临界能量使样品正带电的低能电子束辐照下，由于样品内沉积正电荷，样品的负电荷较快得到中和，表面电位将趋于0电位。

3)电子束能量会影响中和过程的暂态时间，电子束实际着陆能量接近使电子总产额取最大值的入射能量时，中和过程暂态时间呈现极小值；束流越大，中和过程更快达到平衡。这一结果表明通过选择合适的入射能量和束流，更容易实现材料的负电荷中和。