基于增量动态逆的倾转旋翼飞行器飞行控制律设计

2020-01-08郑琛唐鹏李秋实

兵工学报 2019年12期

郑琛，唐鹏，李秋实

(1.北京航空航天大学能源与动力工程学院，北京 100191；2.北京航空航天大学交通科学与工程学院，北京 100191)

0 引言

倾转旋翼飞行器具备直升机垂直起降与固定翼飞机高速巡航的优点，能够在山地、舰艇等复杂地形进行起降，其运输成本比常规直升机和固定翼飞机更低。因此，倾转旋翼飞行器备受世界各国关注[1-4]。然而，倾转旋翼飞行器在建模和控制方面比固定翼飞机和旋翼机更为复杂。一方面，倾转旋翼飞行器气动特性和稳定性会随发动机倾转角度和飞行速度的变化发生明显改变，其气动模型难以精确建立，且变化过程具有很强的非线性特点[5]；另一方面，倾转旋翼飞行器在过渡模式下的操纵既需通过气动舵面又需通过推力矢量舵面，故其还存在操纵冗余的问题[6-7]。

针对倾转旋翼飞行器的控制研究，特别是过渡过程的控制方案研究，国内外学者提出了一些解决办法：文献[8]提出采用多目标非线性规划控制方法解决倾转旋翼飞行器操纵冗余问题，并采用经典线性PID控制器实现稳定的飞行控制；文献[9]采用状态反馈结合补偿矩阵设计姿态内回路，用PI控制设计外回路；文献[10]提出基于平均驻留时间方法研究倾转旋翼飞行器过渡飞行过程的有限时间切换控制问题。虽然上述方法能够使得飞行器达到稳定的控制效果，但文献中也提到了由于过渡模式复杂的非线性特点，单一线性控制器无法达到理想控制效果的问题，需要通过增益调度针对各个状态进行参数调节，其设计工作量大、耗时长。针对这一问题，也有学者提出采用粒子群优化(PSO)算法来优化不同状态下的增益，减少设计调参的工作量[11]。

非线性增量动态逆(INDI)是近年来研究飞行器非线性控制律的算法之一，其通过非线性对消来实现系统的线性化。相比于动态逆算法，INDI方法降低了对精确数学模型的依赖，能保证控制的鲁棒性[12]；相比于PID控制器，其无需进行大量的增益调度，相对减少了工作量。荷兰Delft大学Chu团队将INDI方法运用于多旋翼飞行器的控制律设计上，并通过飞行实验验证了所设计控制律的有效性[13]。陈海兵等尝试将INDI方法应用于飞机大迎角机动飞行控制律的设计[14]；白瑜亮等将INDI方法应用于水下运载器出水姿态的控制律设计中,考虑海浪作用、水动力参数摄动以及噪声观测的影响下，验证了该控制律的有效性[15]；张军等将INDI方法应用于高超声速飞行器载入鲁棒控制律设计，并引入线性跟踪- 微分器解决INDI控制律所需状态速率无法测量的问题[16]。

本文以某倾转三旋翼无人机为例，针对该倾转旋翼飞行器操纵冗余的特点，尝试在INDI控制律中引入舵面控制分配算法，从而实现倾转旋翼飞行器从旋翼模式到固定翼模式的平稳转换。

1 INDI算法构建

1.1 INDI控制律

将无人机转动动力学方程写成如下形式：

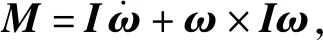
(1)

M=Ma+Mr,

(2)

进而可将(1)式、(2)式合并写成状态方程形式：

(3)

Ma由无人机气动导数和飞行状态计算得到，是造成控制中参数不确定性的主要原因[17]。为解决该问题，在某一状态点(ωp，δp)的邻域内对(3)式进行Taylor展开，得到1阶近似表达式：

(4)

(5)

定义控制效率矩阵

(6)

dδ=(δ-δp),

(7)

则(5)式可以改写成

(8)

1.2 舵面指令分配算法

倾转旋翼飞行器的控制舵面一般包含两部分。一部分为气动舵面，即副翼δa、升降舵δe、方向舵δr；另一部分为推力矢量舵面，即各个发动机及其对应的倾转角度。本文提出的舵面指令分配算法核心思想是将上述两部分控制舵面在不同飞行状态下进行权限分配，并采用再分配伪逆算法对(8)式进行求解。

倾转旋翼飞行器根据旋翼状态可分为多旋翼模式、固定翼模式和过渡模式。多旋翼模式时，飞行器操作依靠推力矢量舵面；固定翼模式时，飞行器操作依靠气动舵面；过渡模式时，飞行器操作即依靠推力矢量舵面，又依靠气动舵面。推力矢量舵面的操纵效率主要受发动机倾转角度影响，气动舵面的操纵效率主要受空速影响。如果将空速和发动机倾转角度合理地联系在一起，则能定量地分析上述2套控制舵面对各轴向力矩产生的操纵效率，进而可以进行操纵权限分配。

(9)

式中：规定发动机推力方向垂直于机身时τ为90°，水平于机身时τ为0°.

此外，根据飞行器配平结果，确定进入和退出过渡模式时的俯仰角分别为θi、θo，并在过渡飞行过程中给出俯仰角线性增加的控制指令。设定过渡模式为定高飞行，滚转角设定为0°，偏航角维持不变。根据前述关系，就可求得各个操纵舵面随飞行速度增加与俯仰力矩L、滚转力矩M和偏航力矩N的变化关系(即操纵导数)。最后，根据操纵导数变化曲线，即可分析得出2套舵面随飞行速度变化时的权限分配系数。

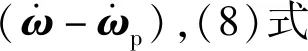
将(8)式转化为如下形式：

Δv=BΔu，

(10)

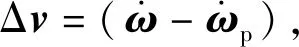
Δu=B†Δv.

(11)

由于实际飞行器中各个操纵舵面具有速率限制和位置限制，直接用伪逆法设计的分配器可能会超出舵面偏转速率、位置限制达到饱和，从而使分配器对转矩可达集的分配效率较低。本文在伪逆法基础上对分配结果进行再次分配调节，使伪逆解重新落入执行器的控制子空间。具体算法如下：

步骤1B1=B，Δv1=Δvc.

步骤2Δu2=clip((B1)†Δv1,up),

Δv2=Δv1-B1Δu2,

B2=删除B1中的饱和列。

步骤3Δu3=clip((B2)†Δv2,up)，

Δv3=Δv2-B1Δu3，

B3=删除B2中的饱和列。

⋮

步骤nΔun=clip((Bn-1)†Δvn-1,up),

Δvn=Δvn-1-B1Δun.

结束。

其中：up为当前舵面偏转量；clip((Bi-1)†Δvi-1,up)是指首先将((Bi-1)†Δvi-1)计算得到的数组各元素与对应的速率限制幅值(即舵面偏转速率限制)做比较。若元素的值超过了速率限制值范围，则意味着Δui中该位置的值达到饱和，应取为对应的速率限制值；若元素的值在限制值范围内，则Δui中该位置的值取为0.在经过上述操作得到Δui后，再令(up+Δui)计算得到的数组各元素与对应的舵面位置限制幅值做比较，若元素的值超过位置限制范围，则Δui中该位置的值取up与位置限制值的差值；若元素的值在位置限制值范围内，则Δui中该位置的值依旧取为0.“Bi=删除Bi-1中的饱和列”是指将Bi中对应于Δui中饱和元素位置的列删除，即在下一步计算中不再考虑偏转饱和的舵面。当Δun中所有元素都饱和或者Δvn=0时计算结束。从而当伪逆法给出的分配结果超出操纵面的速率、位置限制时，可以根据上述算法找出新的一组解，使其能够满足舵面偏转的要求。

2 控制律系统设计

2.1 在线B阵解算

在控制律中，控制效率矩阵B会随着飞行状态和舵面位置的变化而变化，为了能获得飞行中实时的B阵，本文采用实时解算方法，具体算法如下。

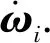
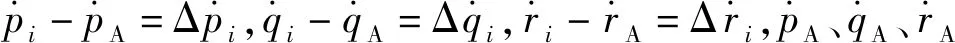
(12)

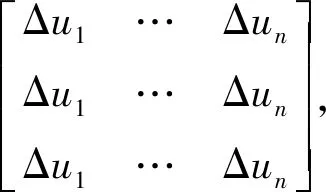
(13)

B=ΔW./ΔU，

(14)

式中：“./”表示矩阵对于元素相除。

通过上述算法，在建立飞行器动力学方程后，只要根据飞行状态和舵面位置，便可求得实时的控制效率B阵。

2.2 控制律设计

本文根据状态变量动态响应过程的时间尺度差异采用层叠结构控制的思想，将控制系统分为慢变化的高度和速度控制、较慢变化的姿态角控制和快变化的姿态角速度控制3部分。

外回路包括高度和速度控制，本文外回路采用经典PID控制。在多旋翼模式下，速度回路作为姿态回路的外回路，高度回路由油门控制；在固定翼模式下高度回路作为姿态回路的外回路，速度回路由油门控制；在过渡模式下，滚转角设定为0°，偏航角维持不变，俯仰角根据配平结果由θi逐渐增加至θo，由于要求在过渡过程中保持高度不变，对前飞速度要求不如高度控制那么严格，另外配平所得到的油门输入可以满足前飞加速要求，速度采用开环控制。经典PID控制器设计本文不做详细说明。

针对本文研究的这类小型无人机，在速率变化方面，快回路带宽一般为较慢回路带宽的5～10倍。慢回路控制器输出的期望指令为姿态角指令ATTc.

令xs=[φ,θ,ψ]T,xsc=ATTc=[φc,θc,ψc]T,定义跟踪误差：

则较慢回路输出的期望角速度指令ωc可表示为

式中:K1=diag(Kφ,Kθ,Kψ)为较慢回路带宽量，一般在1～2 rad/s，本文Kφ、Kθ、Kψ分别取为1.5 rad/s、2.0 rad/s、1.5 rad/s.

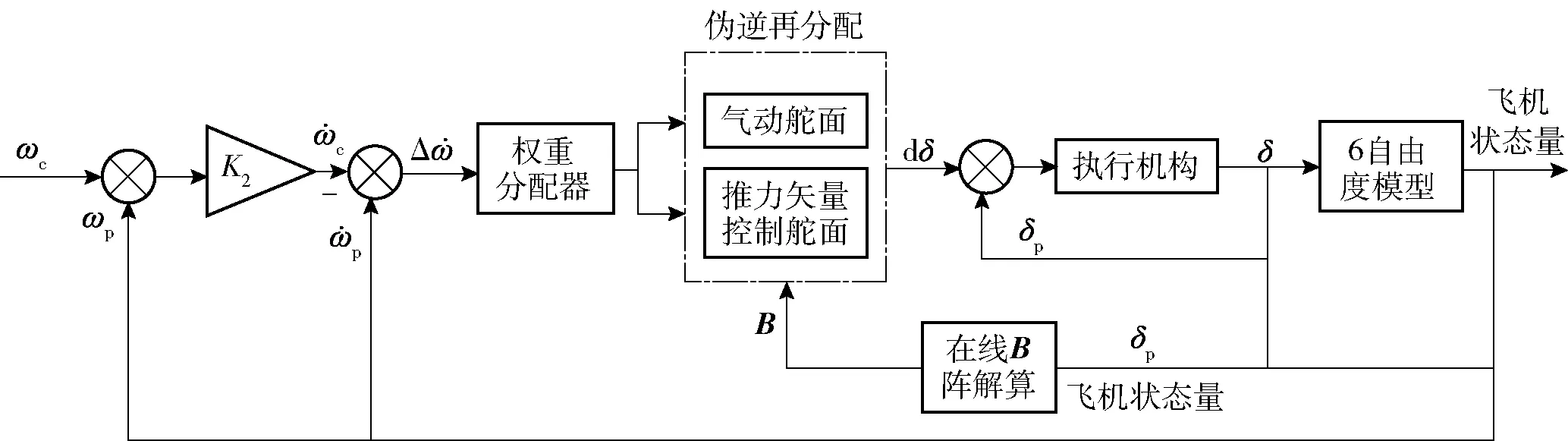
图1 角速度控制方框图Fig.1 Block diagram of angular velocity control

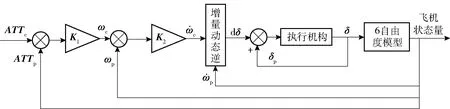
图2 姿态控制方框图Fig.2 Block diagram of attitude control

3 算例飞行器仿真验证

3.1 算例飞行器

以自行设计的电动倾转旋翼飞行器(见图3)为例设计飞行控制律。

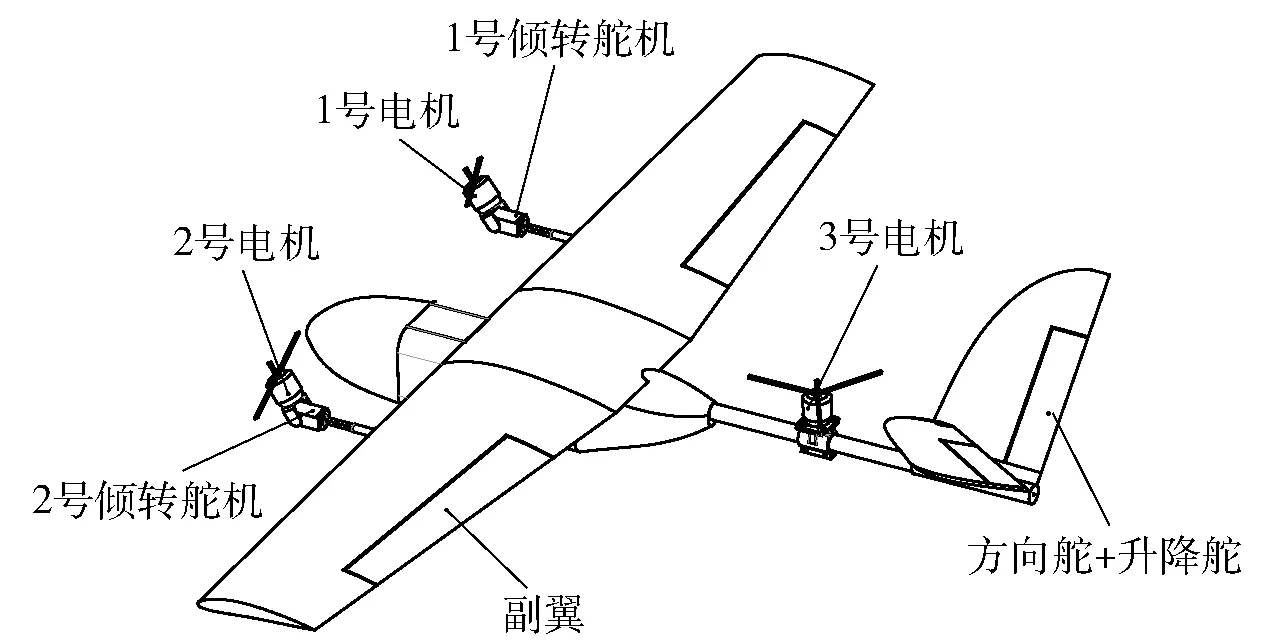
图3 倾转旋翼飞行器Fig.3 Tilt-rotor aircraft

该飞行器的控制输入矢量为

ui=[δe,δa,δr,δt1,δt2,δt3,δb,δd]T，

式中：δe为升降舵；δa为副翼；δr为方向舵；δt1为1号电机推力，可由1号倾转舵机进行倾转；δt2为2号电机推力，可由2号倾转舵机进行倾转；δt3为3号电机推力，固定不倾转；1号、2号电机差动倾转可以产生滚转力矩L和偏航力矩N.δb为1号、2号电机的共同基准倾角，其作用是控制样例飞行器的飞行模式。δb=90°时飞行器处于多旋翼模式，0°<δb<90°时飞行器处于过渡模式，δb=0°时飞行器处于固定翼模式；δd为1号、2号电机的共同偏差倾角，即电机实际倾转角τ与基准倾角的差值，其作用是产生滚转力矩L和偏航力矩N.规定1号电机倾转角τ1=δb+δd、2号电机倾转角τ2=δb-δd.

采用本文方法进行计算分析，设定飞行器进入过渡模式速度ui和退出过渡模式速度uo分别为

ui=5 m/s,uo=15 m/s,

根据配平结果，多旋翼模式5 m/s前飞时俯仰角为-2°，固定翼模式15 m/s前飞时俯仰角为3.5°，考虑到姿态指令跟踪的延迟问题，设定倾转过程中俯仰角从θi=-2°线性地增加至θo=5°.根据此关系，可以求得各个操纵舵面输入与俯仰力矩L、滚转力矩M和偏航力矩N的变化关系，如图4～图6所示。图4～图6中，δtx、δtz分别表示1号、2号电机推力在机体x轴、y轴方向上的差动，δty表示前后电机推力在y轴方向的差动。

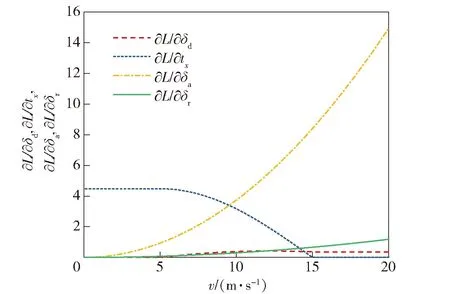
图4 操纵舵面与滚转力矩L的操纵导数Fig.4 Manipulating derivatives of steering surface and rolling moment L

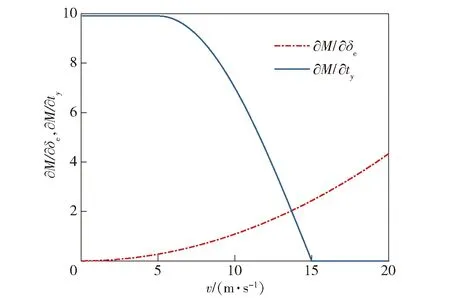
图5 操纵舵面与俯仰力矩M操纵导数Fig.5 Manipulating derivatives of steering surface and pitch moment M

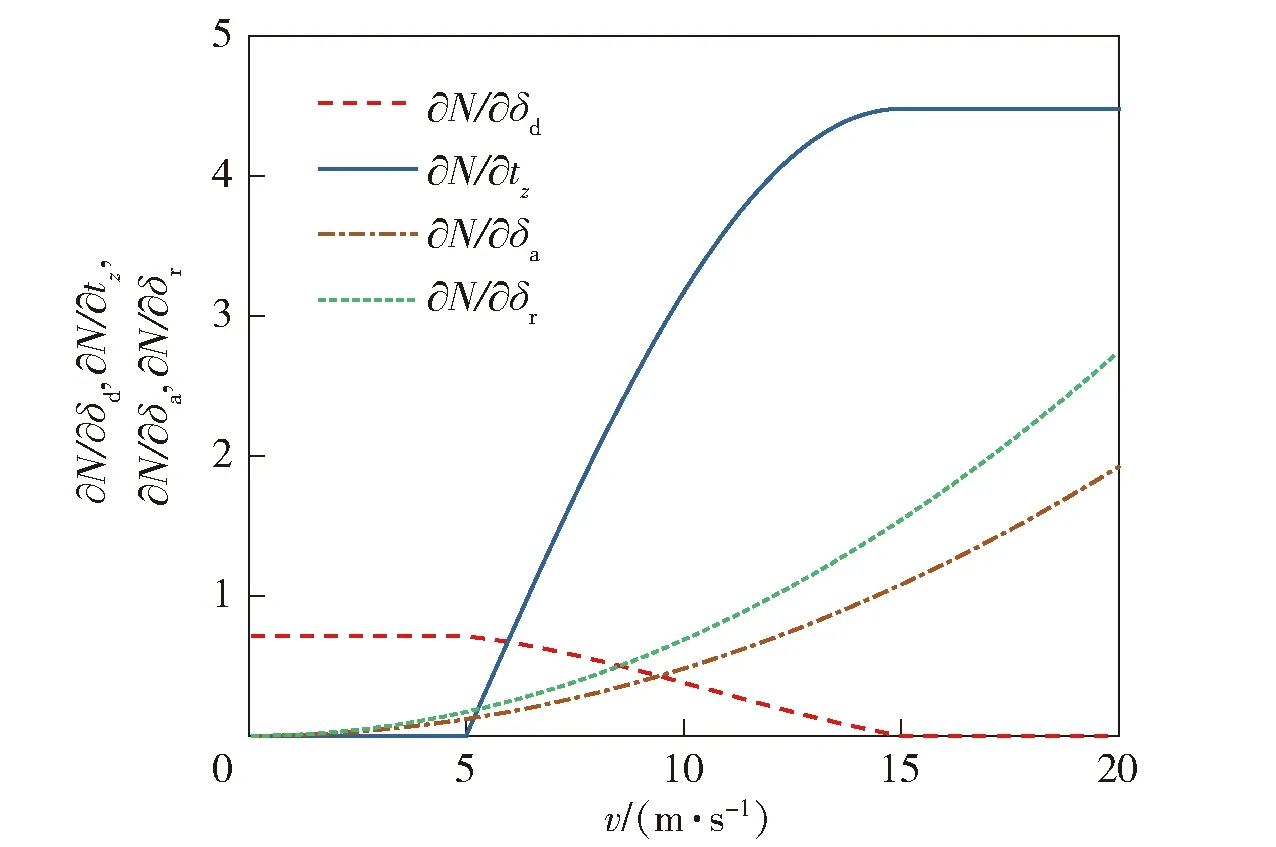
图6 操纵舵面与偏航力矩N的操纵导数Fig.6 Manipulating derivatives of steering surface and yaw moment N

分析各操纵导数随前飞速度的变化可以看出：过渡模式下，随着前飞速度的增加，气动舵面的操纵效率不断增强，推力矢量舵面的操纵效率不断减弱。综合考虑各舵面的操纵效率变化，给出各通道的权限系数如下：

1)滚转通道

(15)

(16)

2)纵向通道

(17)

(18)

3)偏航通道

(19)

(20)

式中：Kslat、Kslon、Ksrud分别表示推力矢量舵面对各轴向力矩的操纵权限系数；Kplat、Kplon、Kprud分别表示气动舵面对各轴向力矩的操纵权限系数。需要注意的是，上述权限分配系数是在假设倾转角和空速具有确定对应关系情况下获得的，由于速度是开环控制，实际仿真或飞行中上述假设可能不成立，因此在仿真中可以根据仿真情况适当调整权限分配系数的值。

3.2 无干扰条件下仿真

利用本文方法设计算例飞行器的全模式控制律并进行仿真验证。飞行控制指令包括多旋翼模式悬停、低速前飞、从多旋翼模式过渡到固定翼模式、固定翼模式定速巡航。仿真飞行过程：t=0 s 时，飞行器高度为100 m并以多旋翼模式悬停5 s，接着用5 s时间加速到5 m/s，然后以5 m/s的前飞速度飞行5 s，从第15 s开始进入过渡模式，基准倾角δb以18(°)/s的速率向下倾转，第20 s时飞行器退出过渡模式并进入固定翼模式，前飞速度回到设定的巡航速度u=15 m/s，持续飞行15 s.整个飞行期间高度指令Hc=100 m，侧飞速度指令vc=0 m/s，滚转角指令φc=0°，偏航角指令ψc=0°，飞机各参数变化曲线如图7～图14所示。

图7 1号电机、2号电机倾转角响应Fig.7 Tilt angle responses of No.1 and No.2 motors

图8 前飞速度响应Fig.8 Forward flight speed response

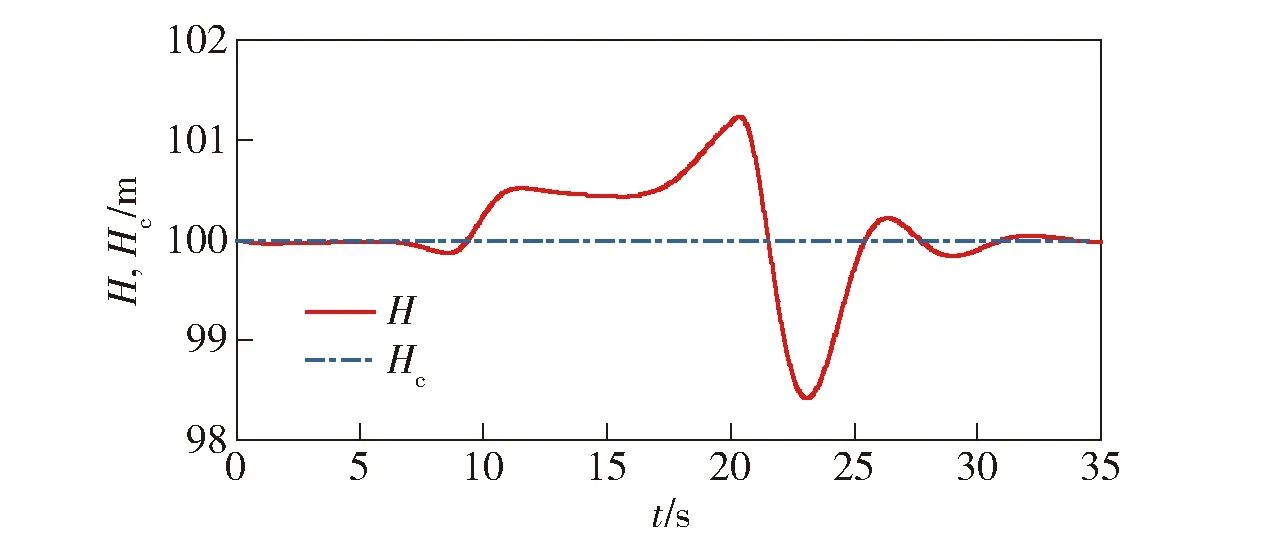
图9 高度状态响应Fig.9 Altitude state response

图10 俯仰角响应Fig.10 Pitch angle responses

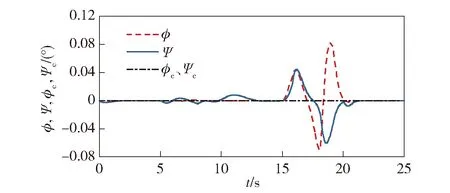
图11 滚转角、偏航角响应Fig.11 Roll and yaw angle responses

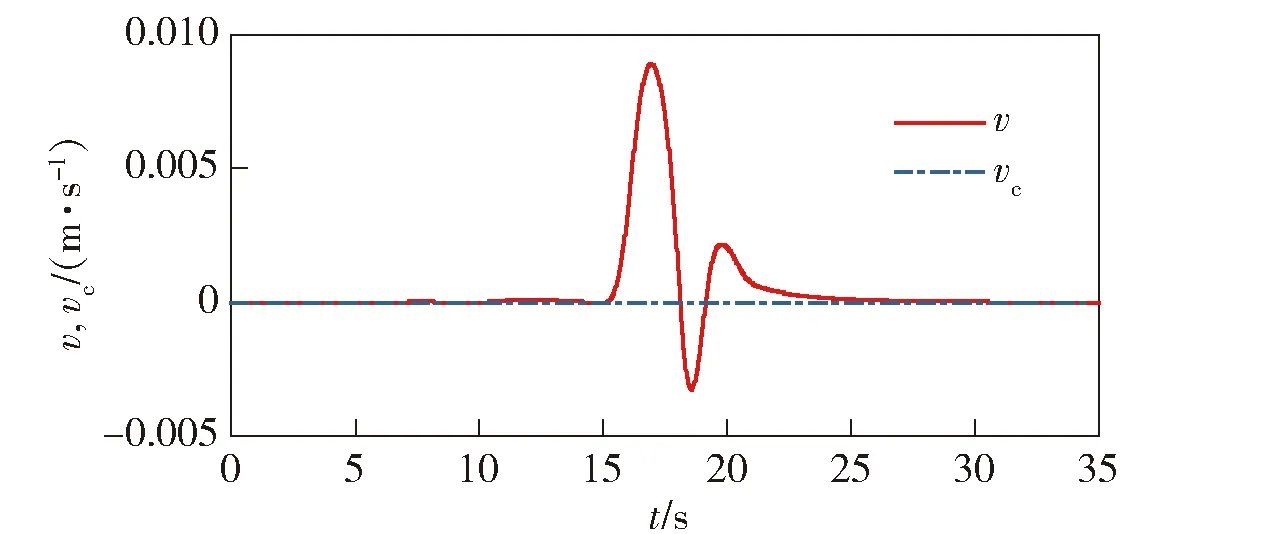
图12 侧飞速度响应Fig.12 Side flight speed response

3.3 存在气动参数摄动情况仿真

引入气动参数摄动情况下的仿真初始条件以及仿真过程与无干扰条件下的仿真一致，当飞行器俯仰力矩曲线斜率Cmα和气动导数Cmδe都摄动为原来的0.8倍，仿真曲线如图15～图21所示。

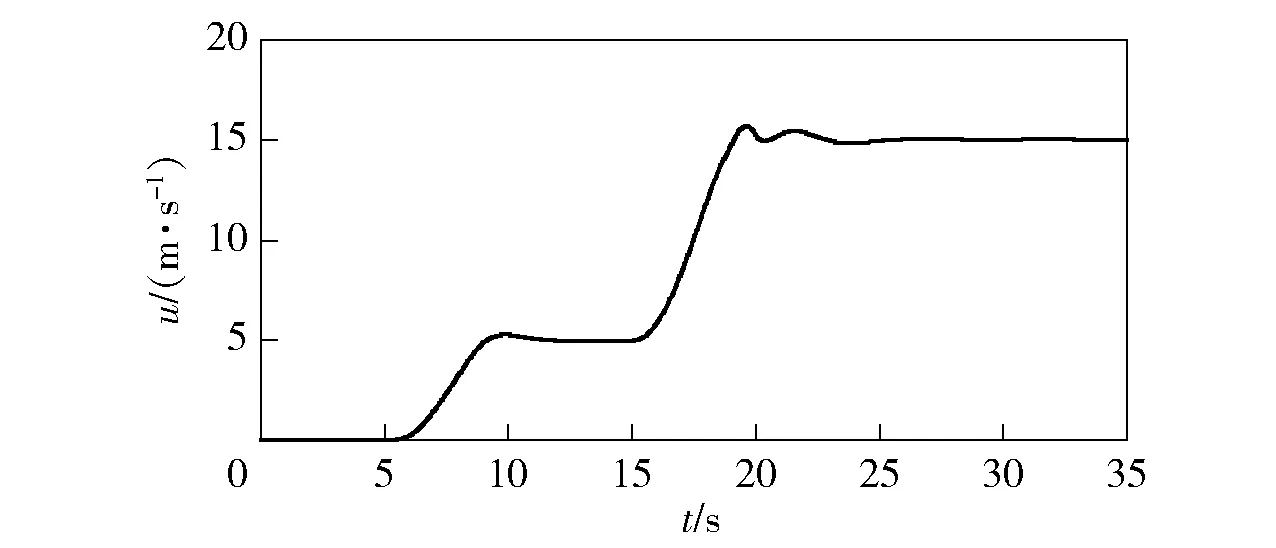
图15 前飞速度响应(存在气动参数摄动)Fig.15 Forward flight speed response (aerodynamic parameter perturbation)

图16 高度响应(存在气动参数摄动)Fig.16 Altitude state response (aerodynamic parameter perturbation)

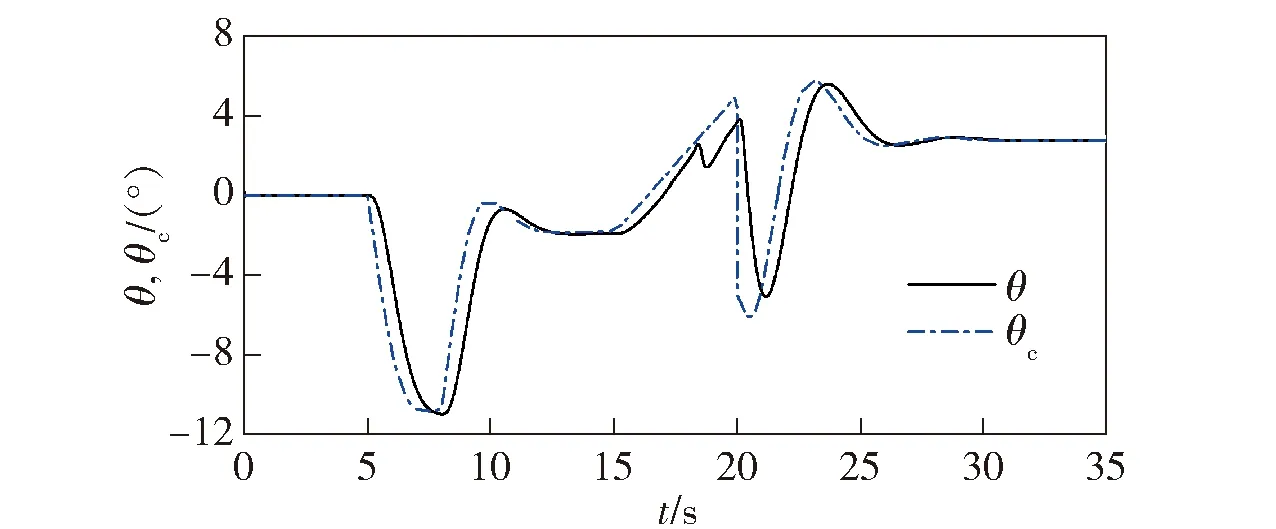
图17 俯仰角响应(存在气动参数摄动)Fig.17 Pitch angle response (aerodynamic parameter perturbation)

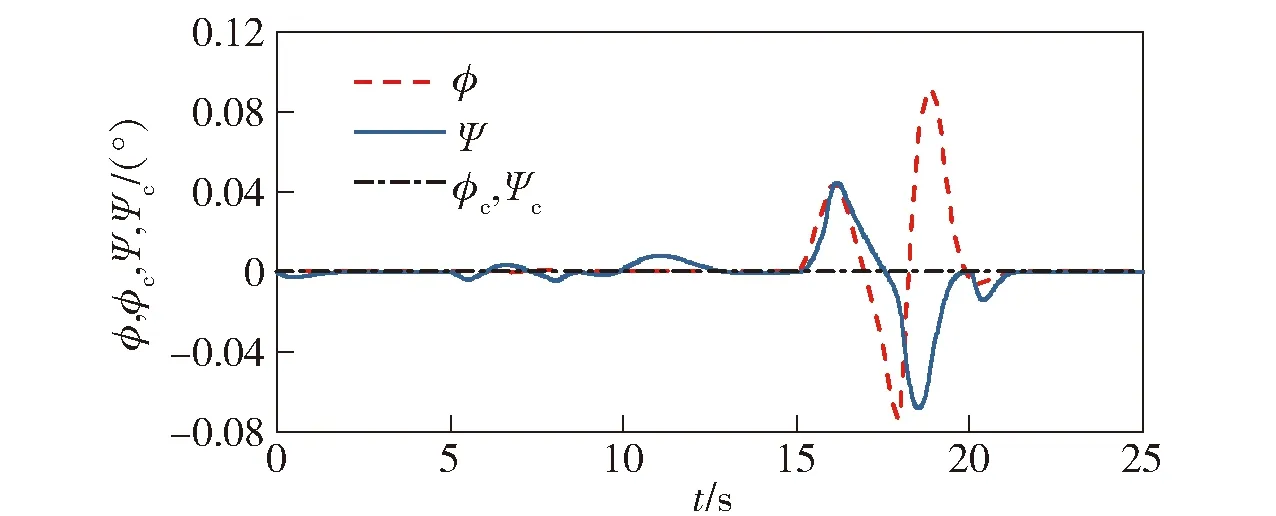
图18 滚转角、偏航角响应(存在气动参数摄动)Fig.18 Roll and yaw angle responses (aerodynamic parameter perturbation)

图19 侧向速度响应(存在气动参数摄动)Fig.19 Side flight speed response (aerodynamic parameter perturbation)

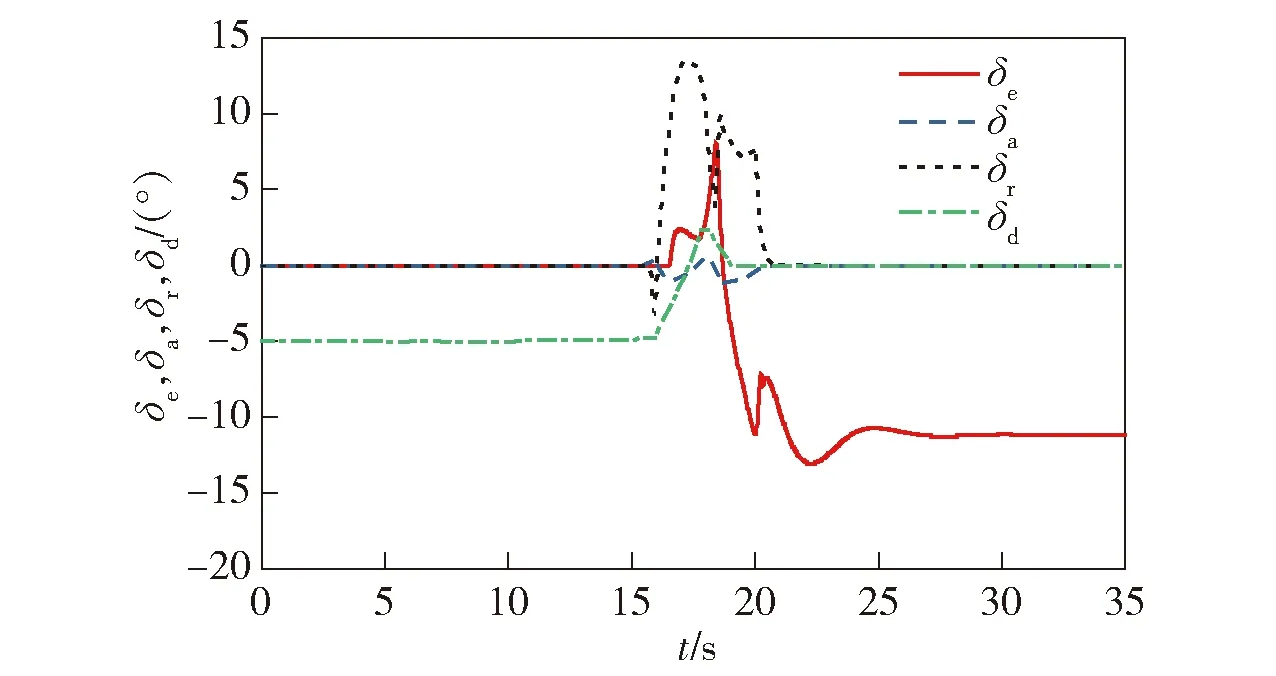
图20 气动舵面及偏差倾角响应Fig.20 Aerodynamic rudder surface and δd responses

图21 各电机推力响应Fig.21 Thrust response of each motor

3.4 存在阵风情况仿真

在过渡模式中引入阵风干扰模型：

式中：W表示风速，仿真中为逆风；Wm为突风强度；tm为突风尺度。取Wm=5 m/s，tm=5 s.

仿真初始条件以及仿真过程与无干扰条件下的仿真一致，仿真曲线如图22～图28所示。

图22 前飞速度响应(存在扰动)Fig.22 Forward flight speed response (with perturbation)

图23 高度响应(存在扰动)Fig.23 Altitude state response (with perturbation)

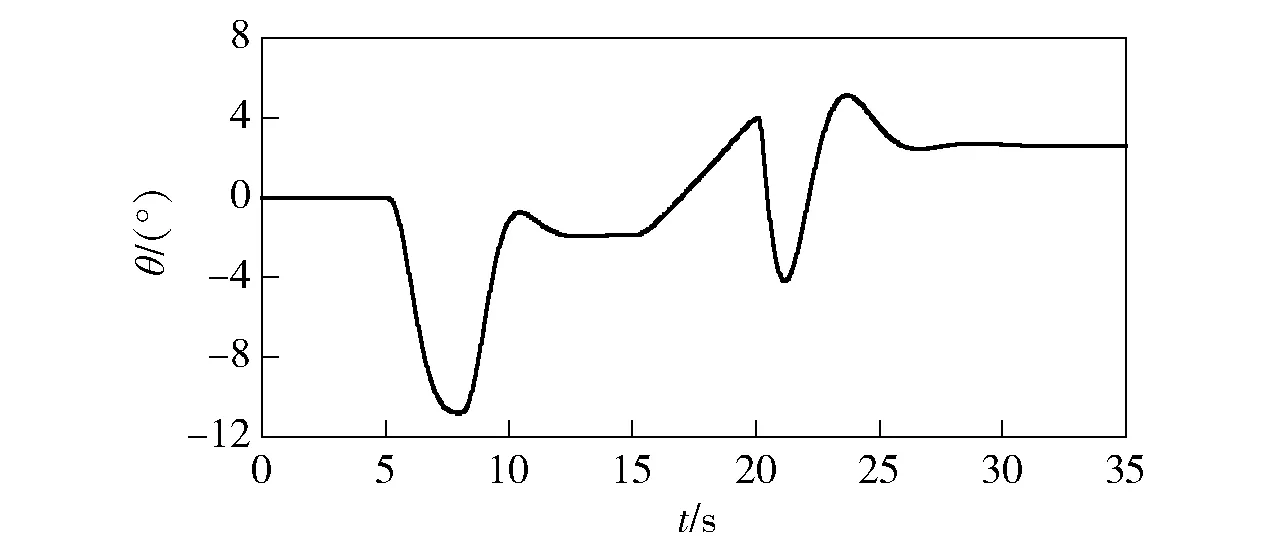
图24 俯仰角响应(存在扰动)Fig.24 Pitch angle response (with perturbation)

图25 滚转角、偏航角响应(存在扰动)Fig.25 Roll and yaw angle responses (with perturbation)

图26 侧向速度响应(存在扰动)Fig.26 Side flight velocity response (with perturbation)

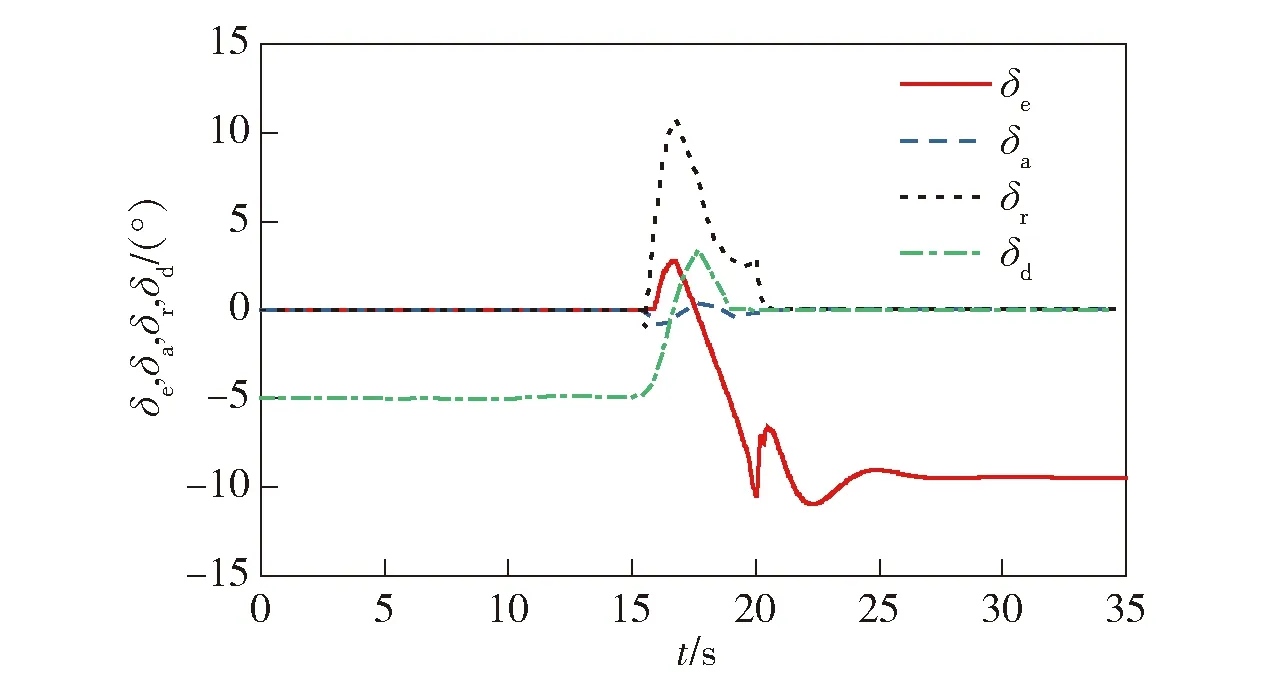
图27 气动舵面及偏差倾角响应(存在扰动)Fig.27 Aerodynamic rudder surface and δd responses (with perturbation)

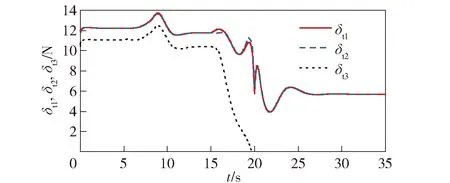
图28 各电机推力响应(存在扰动)Fig.28 Thrust response of each motor (with perturbation)

从无干扰条件下飞行器各状态量的仿真曲线可以看出，在过渡模式下，1号、2号电机倾转角逐渐从90°倾转至0°.在整个过程中，飞行高度能实现了良好的跟踪，最大高度误差为1.6 m，且没有剧烈震荡。由于速度是开环控制，在过渡模式后期速度略微超过了设定巡航速度15 m/s，但依旧处在“倾转走廊”速度范围内，且固定翼模式下速度能很快到回到15 m/s进行定速巡航。俯仰角响应动态良好，俯仰角与指令之间约有0.5 s的时间延迟，这与本文采用的Kθ=2 rad/s较慢回路带宽是一致的。整个飞行过程中，滚转角、偏航角和侧向速度变化很小，保证了倾转过程无侧滑飞行。

从气动参数摄动情况下飞行器各状态量的仿真结果可以看出，当飞行器俯仰力矩曲线斜率Cmα和气动导数Cmδe都摄动为原来的0.8倍时，俯仰角第17 s时有些回落，但进入固定翼模式时依旧能够快速跟踪指令，高度的响应在过渡阶段基本不变，最大高度误差为1.4 m.飞行器进入固定翼模式后能够快速回到15 m/s进行定速巡航，其余响应曲线变化都很小，依旧能够实现平稳、安全的转换。

从阵风干扰情况下飞行器各状态量的仿真曲线可以看出，由于阵风的存在，过渡模式下飞行器的前飞速度比无干扰情况会慢一些，但进入固定翼模式后依旧能快速进入定速巡航。滚转角和偏航角几乎不变，侧向速度v变化也很小。其余响应曲线基本不变，整体控制效果不变，依旧能够实现平稳、安全的转换。

此外，观察3种情况下的冗余舵面偏转情况可以看出，由多旋翼模式向固定翼模式过渡过程中，各个控制舵面都处于合理的控制角度(推力)范围内，且偏转角度(推力)变化连续过渡，验证了舵面分配算法的有效性。