无人艇非线性航迹鲁棒自适应跟踪控制
2020-01-08骆福宇曾江峰艾宁
骆福宇,曾江峰,艾宁
(中国船舶工业系统工程研究院,北京 100094)
0 引言
水面无人艇(USV)具有体积小、机动性强、作业效率高等优点,在军事和民用领域得到了广泛应用[1-4]。USV为了精确地完成一些复杂任务,如特定线路的自主航行、预设区域的扫描测绘等,都需要执行航迹跟踪控制操作。然而,常规的USV具有欠驱动特性,而且复杂的海洋环境极大地影响着USV的操纵性,这些都为实现精确的航迹跟踪控制提出了挑战。
通常,USV只需要实现平稳的线性航迹跟踪即可满足一般的工程应用需求[5]。具体做法是,提前设定一系列航路点并进行分段线性插值,得到一条由直线路径单元组成的复合线性航迹,然后控制USV进行分段直线航迹跟踪。而在航路点转折处,通过设定可接受圆半径完成航迹单元的切换。线性航迹跟踪简单、易于实现,但无法保证每个航路点的可达性,而且航迹单元切换处参考艏向角的骤变又会使航迹跟踪控制精度严重受损,无法满足高品质的航迹跟踪控制要求。Serret-Frenet坐标系的提出为实现USV的曲线航迹跟踪提供了解决思路,但大多数学者仍局限于具有典型数学形式的曲线航迹跟踪控制研究[6-8],关于由给定航路点生成任意曲线参考航迹的问题却少有人提及。根据预设点进行曲线拟合可以采用样条插值技术,常用的插值方法有B样条插值、自然样条插值等[9-10]。B样条插值拟合出的曲线并不通过所有插值点;自然样条插值可以拟合出通过所有插值点的光滑曲线但不具备局部控制能力,改变某一个插值点将会影响到整条插值曲线。航迹跟踪控制系统的另外两个重要组成部分是制导律和控制器[11]。视线(LOS)法是一种有效的制导策略,已经普遍应用于USV的航迹跟踪控制中[5,12]。文献[13]考虑环境干扰力的影响,提出了积分LOS制导方式,但着眼于解决线性航迹跟踪问题。对于控制器问题,常用方法是分别设计PID控制器进行航向和航速控制。也有学者采用反步法或径向基神经网络(RBFNN)等控制方式[7-8,14],但反步法过于依赖USV的精确数学模型,传统RBFNN为了保证较高的逼近精度往往需要设置大量网络节点,从而导致在线自适应参数过多而计算量过大、实时性较差。
基于以上分析,本文研究一类欠驱动USV的非线性航迹跟踪控制问题,旨在提高航迹跟踪控制的精度和品质。首先根据预设航路点采用单调3次埃尔米特样条插值(CHSI)技术进行航迹拟合,获得一条通过所有航路点且具有保形能力的非线性曲线航迹;然后在Serret-Frenet坐标系框架下,设计考虑航迹曲率影响的自适应LOS制导律以及基于最小学习参数思想的RBFNN动力学控制器。与传统RBFNN相比,本文中每个神经网络的自适应学习参数只有1个,而与网络节点数无关,能够有效地减轻网络计算负担。通过稳定性分析证明了系统的一致最终有界性,并通过仿真实例验证了所提出控制方案的有效性。
1 问题描述
欠驱动USV的水平面3自由度运动数学模型可以表示[10,15]为
(1)
式中:x、y、ψ分别为USV在大地坐标系{E}下的纵向位置、横向位置和艏向角;u、v、r分别为USV在艇体坐标系{B}下的前进速度、横向速度和艏摇角速度;τu、τr分别为施加于USV艇体上的控制力、控制力矩;duE、dvE分别为作用于USV 2个自由度u、v上的环境干扰力,drE为作用于USV自由度γ上的干扰力矩;Fu(v,r)、X(u)、Y(u)、Fr(u,v,r)均为未知非线性函数,
(2)
正常量m11、m22、m23、m33、d11、d22、d23、d32、d33表示USV的模型参数,分别描述USV的质量、附加质量和水动力阻尼。本文假设USV的模型具有任意不确定性,因此模型参数以及非线性函数项的结构完全未知。
为了便于控制器的设计与分析,本文引入以下假设与引理。
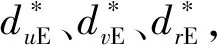
假设2USV的横向速度v具有一致耗散有界性[16]。
假设3USV的艏向控制器能够实现对期望艏向角的精确跟踪[17]。
需要指出的是,对于通常的USV等水面船舶,假设1和假设2总是成立的。环境干扰力主要由风、浪和流等引起,在很大程度上归因于外部效应,具有有限能量,因此是有界的。文献[16]针对典型的船舶横向动力学模型,对横向速度v的有界性已经给出了系统性分析和证明。引入假设3的主要目的是便于分析USV的航迹跟踪误差,假设3可以通过调整USV的艏向控制器参数来保证。
引理1[18]RBFNN能够在紧集ΩZ∈Rn(n为正整数)中逼近任意的光滑、连续函数f(Z),即
f(Z)=W*TH(Z)+ε,∀Z∈ΩZ,
(3)

(4)
W=[w1,w2,…,wl]T∈Rl为RBFNN的权值向量,l为节点数;H(Z)=[h1(Z),h2(Z),…,hl(Z)]T∈Rl为基函数向量。基函数的形式有多种,一般选择高斯函数,其形式为
(5)
式中:bj为基函数宽度,j=1,2,…,l;cj=[cj1,cj2,…,cjn]T∈Rn为基函数中心。
USV的非线性航迹跟踪控制目标可以描述为:根据规划系统提供的航路点信息,通过插值算法拟合出一条光滑、连续的非线性曲线参考航迹,并设计相应的制导律和控制器,使USV能够以一定的航速到达并保持在期望航迹之上。
2 非线性航迹拟合
为了生成经过预设航路点的非线性曲线参考航迹,本文采用如下单调CHSI方法进行拟合。
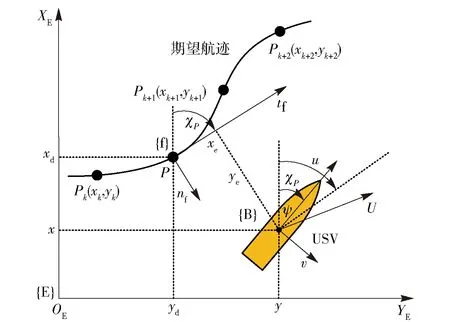
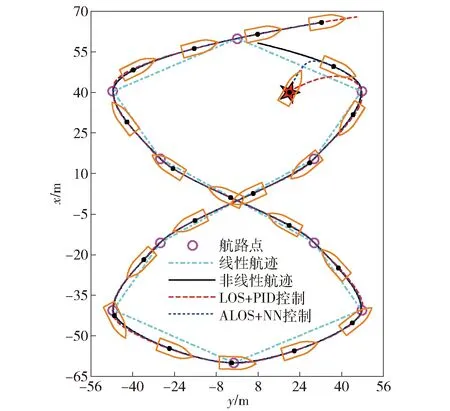
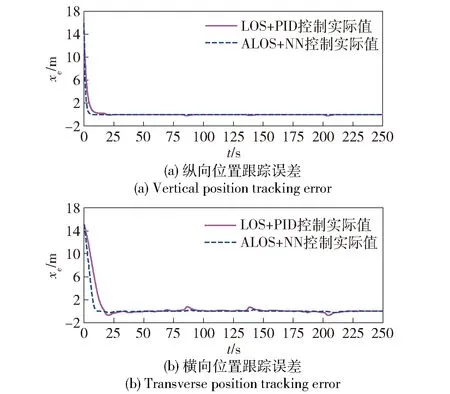
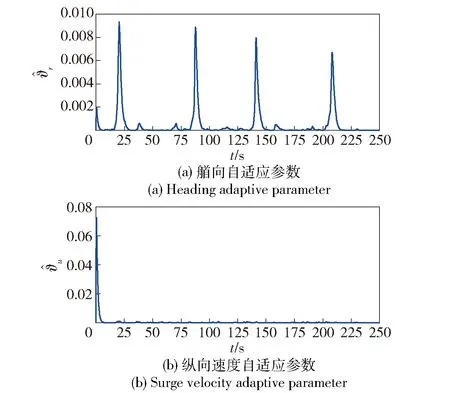
考虑在区间I=[a,b]上存在的n个控制点a=q1 p(qt)=ft,t=1,2,…,n, (6) 式中:p(q)具有单调性,且在每个子区间It=[qt,qt+1]上均是一个3次多项式,其形式[19]为 p(q)=ftH1(q)+ft+1H2(q)+dsH3(q)+ds+1H4(q), (7) 其中,ds=p′(qs)为第s=t或s=t+1个控制点处对应的1阶微分值,H1(q)、H2(q)、H3(q)和H4(q)为子区间It上的3次埃尔米特基函数,即 H1(q)=ζ[(qt+1-q)/ht],H2(q)=ζ[(q-qt)/ht], (8) ht=qt+1-qt,ζ(ω)=3ω2-2ω2,η=ω3-ω2,ω为曲线参数。为保证单调性,控制点处的斜率通过如下方式计算: 定义δt=(ft+1-ft)/ht为子区间It的分段线性插值斜率,如果δt和δt-1符号相反或其中有1个为0,则xt为函数的局部极小或极大点,此时可以取dt=0;如果δt和δt-1符号相同且所对应的子区间长度也相等,则dt的计算公方式为 (9) 如果δt和δt-1符号相同且两个子区间长度不相等,则dt的计算公式为 (10) 式中:ω1=2ht+ht-1;ω2=ht+2ht-1. 将单调CHSI算法用于非线性航迹拟合时,需要另外引入独立变量θ来描述曲线方程。此时,针对定义在笛卡尔坐标系中的一系列航路点坐标P1(x1,y1),…,Pk(xk,yk),…,Pn(xn,yn),k=1,…,n,则通过相邻2个航路点Pk(xk,yk)和Pk+1(xk+1,yk+1)的3次多项式可以插值为 xd(θ)=cx0+cx1(θ-θk)+cx2(θ-θk)2+cx3(θ-θk)3, (11) 式中: (12) 单调CHSI具有很好的形状塑造和保持能力,能够有效地避免航迹曲线在2个连续航路点之间出现摇摆和曲折问题,而且新增加的航路点对整条航迹的影响较小,能更好地满足USV航迹跟踪控制中航路点实时变化的需要。 采用单调CHSI算法和常用的自然样条插值(NSI)算法对5个航路点进行航迹拟合的实例对比,结果如图1所示。由图1可以看到,CHSI算法能够拟合出更优良的参考航迹,而且改变最后1个航路点几乎不会对前面已生成的航迹曲线形状产生影响,从而为实现USV准确、高效的航迹跟踪控制奠定了基础。 图1 航迹拟合对比Fig.1 Path fitting 在大地坐标系{E}中建立如图2所示的局部Serret-Frenet参考坐标系{f},并定义坐标系{f}下的纵向和横向航迹跟踪误差分别为 xe=x-xd(θ),ye=y-yd(θ), (13) 则USV的航迹跟踪误差运动学方程可以表示[7]为 (14) 图2 Serret-Frenet参考坐标系Fig.2 Serret-Frenet reference frame 为了消除航迹跟踪位置误差xe和ye,本文提出如下自适应LOS制导律: (15) 式中:ψd为USV的期望艏向角;yint为关于横向跟踪误差的积分项,且满足|yint|≤ymax;Δ=(Δmax-Δmin)e-kc|c(θ)|+Δmin为前视距离,Δmax、Δmin分别为设计的最大和最小前视距离,kc>0为设计参数,c(θ)=dχP(θ)/dθ为参考目标点处的航迹曲率;k1>0为积分增益。 与传统USV的期望艏向角制导相比,本文设计的制导律更灵活,能够为USV提供一个随航迹曲率和环境干扰力变化的自适应视线角。曲率的引入使得USV在航迹曲线平坦处平缓地趋向期望航迹,而在陡峭处激进地改变航向,更符合USV的实际操舵思想;非0积分项的引入旨在增强USV抵抗环境漂移力的能力,提高航迹跟踪控制精度。 Serret-Frenet坐标系下的航迹跟踪控制需要将参考目标点与USV的运动联系起来。本文将参考目标点的线速度设计如下: (16) 式中:k2>0为设计参数。则对应的航迹曲线参数更新律可以设计为 (17) 定义如下Lyapunov函数: (18) (19) (20) 则给定任意的σ>0,对所有的|ye|≤σ,有 (21) 定义USV的艏向角跟踪误差为 ψe=ψ-ψd, (22) 对(22)式求导,可得 (23) 则虚拟控制律αr可以设计为 (24) 定义艏向角速度跟踪误差为 re=r-αr, (25) 对(25)式求导,并结合USV的动力学方程,可得 (26) 定义函数Φr(Zr)=Fr(u,v,r),其中Zr=[u,v,r]T。由于Φr(Zr)为未知非线性函数,本文采用RBFNN对其进行逼近,则(26)式可进一步写为 (27) (28) 式中:kr>0为设计参数;r为正常量的估计值,为理想权值范数。则将(28)式代入(27)式,可得 (29) 则神经网络自适应参数更新律设计为 (30) 式中:ηr、κr为正的设计参数,则USV的艏向跟踪误差动力学可以描述为 (31) 定义USV的纵向速度跟踪误差为 ue=u-ud, (32) 式中:ud为期望纵向速度大小,通常为定值。对(32)式求导,并结合USV的动力学方程,可得 (33) 定义Φu(Zu)=Fu(v,r)-d11u/m11,其中Zu=[u,v,r]T。由于Φu(u,v,r)为未知非线性函数,采用RBFNN对其进行逼近,则(33)式可进一步写为 (34) (35) 式中:ku>0为设计参数;u为未知正常量的估计值,为理想权值向量的范数。则将(35)式代入(34)式,可得 (36) 则神经网络自适应参数更新律设计为 (37) 式中:ηu、κu为正的设计参数,则USV的纵向速度跟踪误差动力学可以描述为 (38) 定理1考虑(1)式、(2)式所示的欠驱动USV系统,在假设1~假设3满足的条件下,设计如(15)式所示的制导律以及(28)式和(35)式所示的控制律,构建在线学习参数为(30)式和(37)式所示的自适应RBFNN,则航迹跟踪控制系统的所有信号一致最终有界。 证明选择如下Lyapunov函数: (39) 对(39)式求导,并代入(31)式和(38)式,可得 (40) 对(40)式进行不等式放缩[20]并进行整理,可得 (41) 式中:μ、λi和ρi为正常量。 为了分析闭环控制系统的稳定性,定义如下Lyapunov函数: V=V1+V2, (42) 对(42)式求导,并考虑(21)式、(41)式,可得 (43) 其中,φ和ξ为正常量,分别定义为 (44) (45) 由此可见,如果控制参数满足以下条件: (46) 采用文献[21]中的USV模型进行仿真对比研究,该USV质量为15 kg,艇长为1.25 m.其中,由风、浪和流等引起的环境干扰力假定由下列1阶Gauss-Markov过程生成[22]: (47) 式中:cu、cv、cr为设计参数;wu、wv、wr为高斯白噪声。 实例1为了验证本文提出的自适应LOS制导律和神经网络控制器的有效性及优越性,增加传统LOS制导律和PID控制器设计。以LOS+NN、ALOS+NN、ALOS+PID分别表示采用传统LOS加神经网络控制、自适应LOS加神经网络控制、自适应LOS加PID控制3种航迹跟踪控制方案,进行对比分析研究。航迹跟踪控制目标为控制USV跟踪由4个航路点通过CHSI拟合得到的一条S形非线性曲线航迹,预设航路点坐标为 P1=(20 m,20 m),P2=(40 m,50 m), (48) 图3 基于4个航路点的航迹跟踪控制结果对比Fig.3 Path tracking control results based on 4 way-points 图3中的线性航迹为分段线性插值结果,非线性航迹为本文CHSI拟合结果,橙色船行图为USV基于本文所提ALOS+NN控制方案在航迹跟踪过程中位置和艏向变化情况的直观显示。由图3可以看到,3种控制方案都成功地实现了对非线性曲线航迹的跟踪,但3种控制方案的跟踪效果仍然存在一些差异,如图3中的两个局部放大图所示。图3左上角的局部放大图为3种控制方案在第3个航路点处的跟踪细节,可以看出LOS+NN控制方案的跟踪效果较差,而ALOS+NN和ALOS+PID控制方案的跟踪效果较好而且效果几乎完全相同。这主要是因为第3个航路点处的航迹曲率变化较大,而本文所提自适应LOS在制导律设计中考虑了航迹曲率因素,能够在航迹曲率变化较大处为USV提供一个较小的前视距离,以激进地改变航向从而保证较高的跟踪精度。图3右侧的局部放大图为3种控制方案在第3个航路点至第4个航路点之间稳定阶段的跟踪细节,可以看出采用神经网络控制的LOS+NN和ALOS+NN控制方案相对于采用PID控制的ALOS+PID控制方案,具有较高的收敛精度,体现了本文设计的神经网络控制器的优越性。 实例2为了充分测试本文所提航迹拟合和航迹跟踪控制方案的性能,并分析控制系统误差信号的收敛性,选择一条由10个航路点拟合得到的8字型曲线航迹进行仿真对比研究,预设航路点的具体坐标为 P1=(60.00 m,0 m),P2=(40.45 m,47.55 m), (49) 图4 基于10个航路点的航迹跟踪控制结果对比Fig.4 Path tracking control results based on 10 way-points 图4描绘了采用2种控制方案的航迹跟踪控制结果对比。从图4中可以看到,相比于传统的LOS+PID控制方案,ALOS+NN控制方案能够使USV在初始横向位置跟踪误差较大时快速地趋向期望航迹,而在大曲率处以及稳定之后具有较高的跟踪控制精度,体现了本文所提控制方案的优越性。图5给出了2种控制方案在航迹跟踪过程中的位置跟踪误差收敛情况。从图5中可以看出,基于ALOS+NN控制方案的位置跟踪误差具有较快的收敛速度,而且在航迹曲线陡峭处能够明显降低抖振,具有较强的航迹保持能力。 图5 位置跟踪控制结果对比Fig.5 Position tracking control results 图6 艏向角跟踪控制结果对比Fig.6 Comparison of heading angle tracking control results 图7 速度控制结果对比Fig.7 Comparison of velocity control results 图6为航迹跟踪过程中的艏向角跟踪情况对比。由图6可见,本文所提ALOS+NN控制方案在艏向角跟踪方面也具有明显优势。值得注意的是,由于2种控制方案在收敛速度方面存在差异,对应的期望艏向角在演绎过程中存在相位的偏差。图7给出了2种方案在航迹跟踪过程中的USV艏向角速度和纵向速度误差变化情况。由图7可以看到,受环境干扰力的影响,艏向角速度和纵向速度均不可避免地出现了振荡,而且艏向角速度对航迹的变化更敏感。虽然2种方案都能使速度偏差稳定在0值附近,但采用本文控制方案的跟踪误差振动幅度更小、收敛性更好,由此证明了本文设计的自适应神经网络控制器具有较强的鲁棒性。 图8 艏向角跟踪控制结果对比Fig.8 Comparison of heading angle tracking control results 图9 控制输入Fig.9 Control input 图8为本文所提RBFNN控制器的自适应参数变化情况。由图8可以看到,稳定之后的自适应参数能够随航迹曲率以及环境干扰力的变化及时更新,保证具有较好的控制效果。由于本文引入了最小学习参数思想对神经网络的结构进行了优化,使得每个神经网络只含有1个在线学习参数,有效地减轻了网络的计算负载。图9给出了本文提出的控制方法在航迹跟踪控制过程中控制力矩和控制力的变化情况,可以看到,二者均稳定在一定的合理范围之内。 本文针对USV的非线性航迹跟踪控制问题进行研究,提出了一种基于CHSI航迹拟合和RBFNN控制的解决方法。CHSI能够根据预设航路点拟合出一条光滑且具有保形特性的非线性参考航迹,为实现USV的高品质航迹跟踪提供了保障。此外,考虑非线性航迹的曲率因素设计了自适应LOS制导律,并针对USV的模型不确定性及环境干扰力问题开发了基于最小学习参数思想的RBFNN动力学控制器。所提出的控制策略能够有效地改善USV航迹跟踪控制的精度和品质问题,且具有鲁棒性强、运算负载小等优点。最后基于Lyapunov理论分析了系统的稳定性,并开展了仿真对比实例,验证了所提方法的有效性及优越性。 下一步工作将研究考虑避障需求的航迹拟合方法,并开展实艇实验,对本文所提算法进行验证。
H3(q)=-htη[(qt+1-q)/ht],
H4(q)=htη[(q-qt)/ht],
yd(θ)=cy0+cy1(θ-θk)+cy2(θ-θk)2+cy3(θ-θk)3,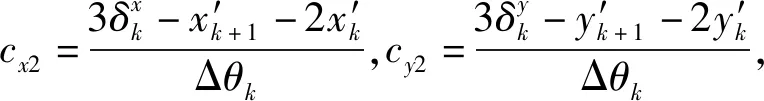


3 航迹跟踪控制
3.1 自适应LOS制导
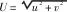
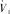


3.2 艏向控制器
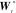

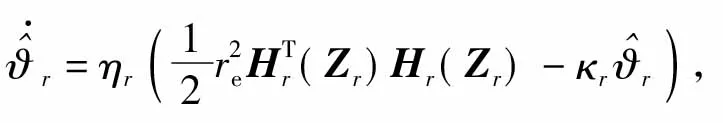

3.3 纵向速度控制器
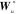

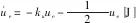

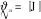
4 稳定性分析
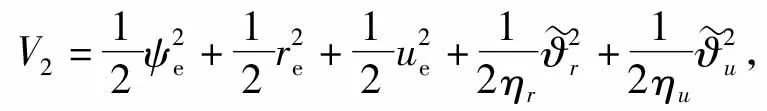
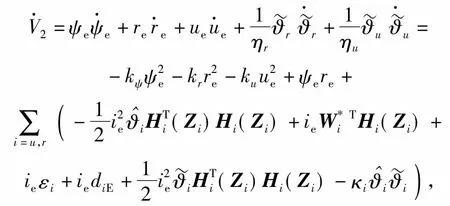

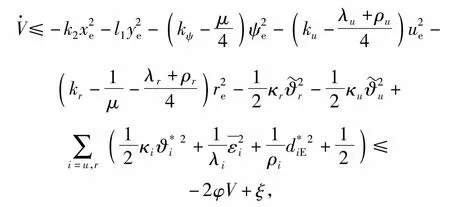

5 仿真实例
P3=(70 m,40 m),P4=(100 m,120 m).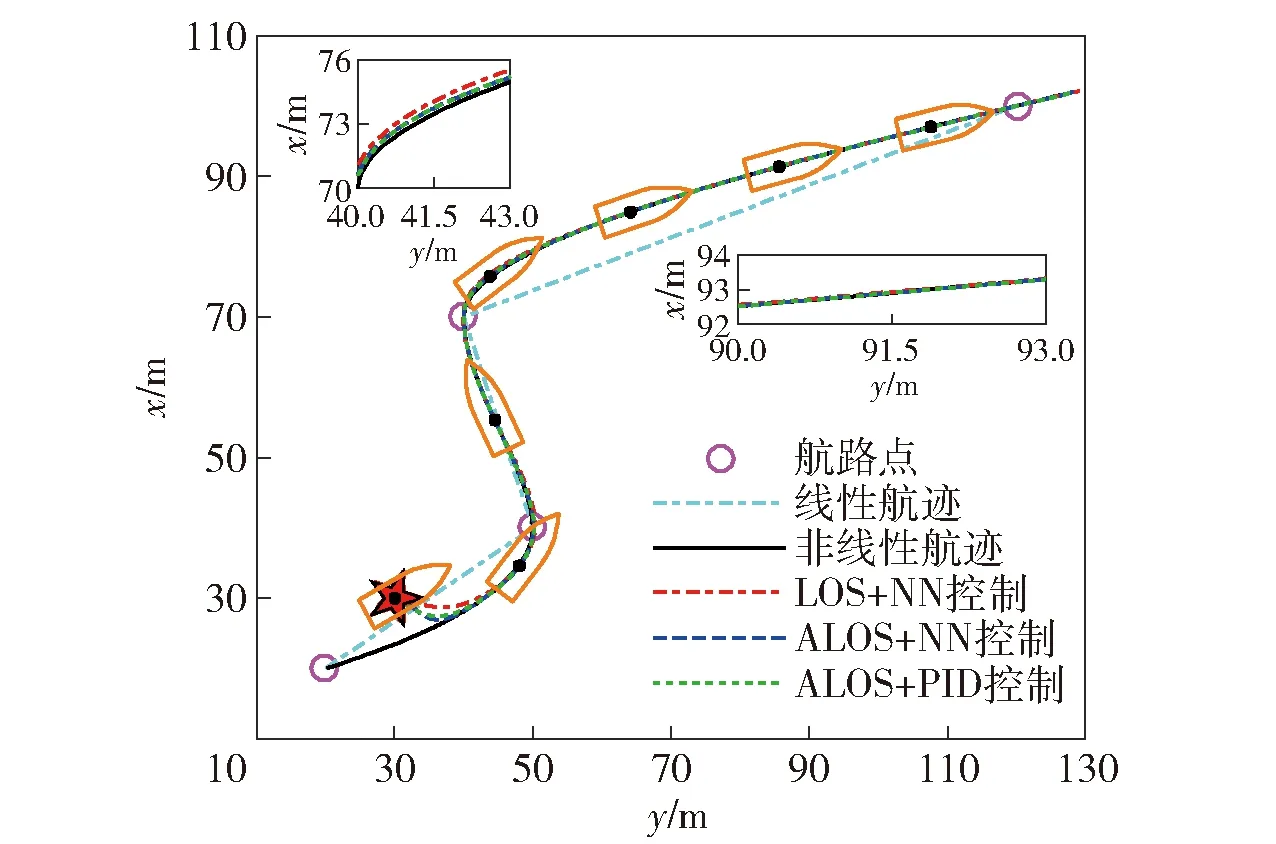
P3=(15.45 m,29.35 m),
P4=(-15.45 m,-29.35 m),
P5=(-40.45 m,-47.55 m),
P6=(-60.00 m,-1.25 m),
P7=(-40.45 m,47.55 m),
P8=(-15.45 m,29.35 m),
P9=(15.45 m,-29.35 m),
P10=(40.45 m,-47.55 m).



6 结论
