无人平台越野环境下同步定位与地图创建

刘忠泽，陈慧岩，崔星，熊光明，王羽纯，陶溢

(1.北京理工大学 机械与车辆学院，北京 100081；2.中国北方车辆研究所，北京 100072；3.北京特种车辆研究所，北京 100072)

0 引言

同步定位与地图创建(SLAM)在无人平台(UGV)领域受到了越来越多的关注。基于视觉的6自由度SLAM[1-2]的性能很容易受到照明和天气变化的影响。因此，一些基于激光雷达的SLAM系统相继出现[3-5]。Alismail等[6]、Besl等[7]将迭代最近邻匹配(ICP)算法加以扩展，从而获得一种适用于考虑样本间姿态误差的连续轨迹估计SLAM方法。Nüchter等[8]提出一种基于三维激光雷达的室外SLAM系统，该算法需要为闭环检测提供一个初始启发值。经典的三维地图模型包括点云地图、点面地图、八叉树地图以及体素栅格地图。其中点云地图可以非常精细地描述三维环境[8-10]，但无法及时处理地图数据以表达环境中的变化；点面地图在表面信息丰富的场景中表现良好[11]，但越野环境中的表面信息非常少。Douillard等[12]将体素地图与粗略的高程地图结合起来处理三维分割问题，但没有良好的组织数据。Wurm等提出了一种新颖的多分辨率方法，基于八叉树来高效地创建三维概率地图[13]，该方法参考了八叉树地图[14]算法。邹斌等[15]利用聚类算法，基于16线激光雷达，应用聚类算法提取了可通行区域，但是该算法对噪声比较敏感。主流的全局位姿优化方法包括基于粒子滤波方法、扩展卡尔曼滤波器(EKF)方法以及基于图论的SLAM.Grisetti等[16]使用粒子滤波方法解决SLAM问题，但基于粒子滤波的SLAM必须在每个粒子中表示整个系统状态，不适合处理大尺度越野场景中的SLAM问题。基于EKF的SLAM[17]强烈地依赖于无人平台的运动假设以及传感器噪声假设，对于自然环境很难实现；基于EKF的SLAM还存在着非线性误差以及计算量不断增大的问题。郭剑辉等[18]采用尺度无迹变换(SUT)改进了基于EKF的SLAM系统，消除了3阶以下的非线性误差，但仍存在着计算量不断增大的问题。基于图论的SLAM方法大多以一组代表无人平台位姿和全局特征点的节点以及连接节点的约束作为处理对象，Kümmerle等[19]基于图论提出了一个g2o优化框架。林俊钦等[20]基于深度相机(RGBD)，利用正态分布变换算法(NDT)提出了一种混合闭环检测方法，但三维激光雷达点云比较稀疏，在小尺度栅格内提取的NDT特征误差较大。由于环境数据大规模性及场景复杂性，SLAM方法很少被设计用于越野环境。

本文提出一个由2个三维激光雷达和1个惯性测量单元(IMU)作为传感器的6自由度激光雷达SLAM系统，该系统能够满足大尺度越野环境中无人平台实时自动驾驶的需求。2个三维激光雷达可以从一次观测中获得更多的环境信息，存在的盲区较小，且雷达点云的运算效率比视觉也要高。该系统分为三维地图创建以及6自由度全局姿态优化两个子系统。在地图创建部分，构建了一张结合三维栅格地图和拓扑地图优点的全局混合地图，用以越野环境实时提取可通行区域。在处理6自由度全局位姿优化问题时，采用稀疏位姿调整[3](SPA)算法来消除激光雷达里程计的累积误差，并提出一种基于分支限界(BBS)法的旋转直方图最近邻匹配(RHM-ICP)实时闭环检测方法，通过闭环检测获得子地图间约束。

1 系统框架

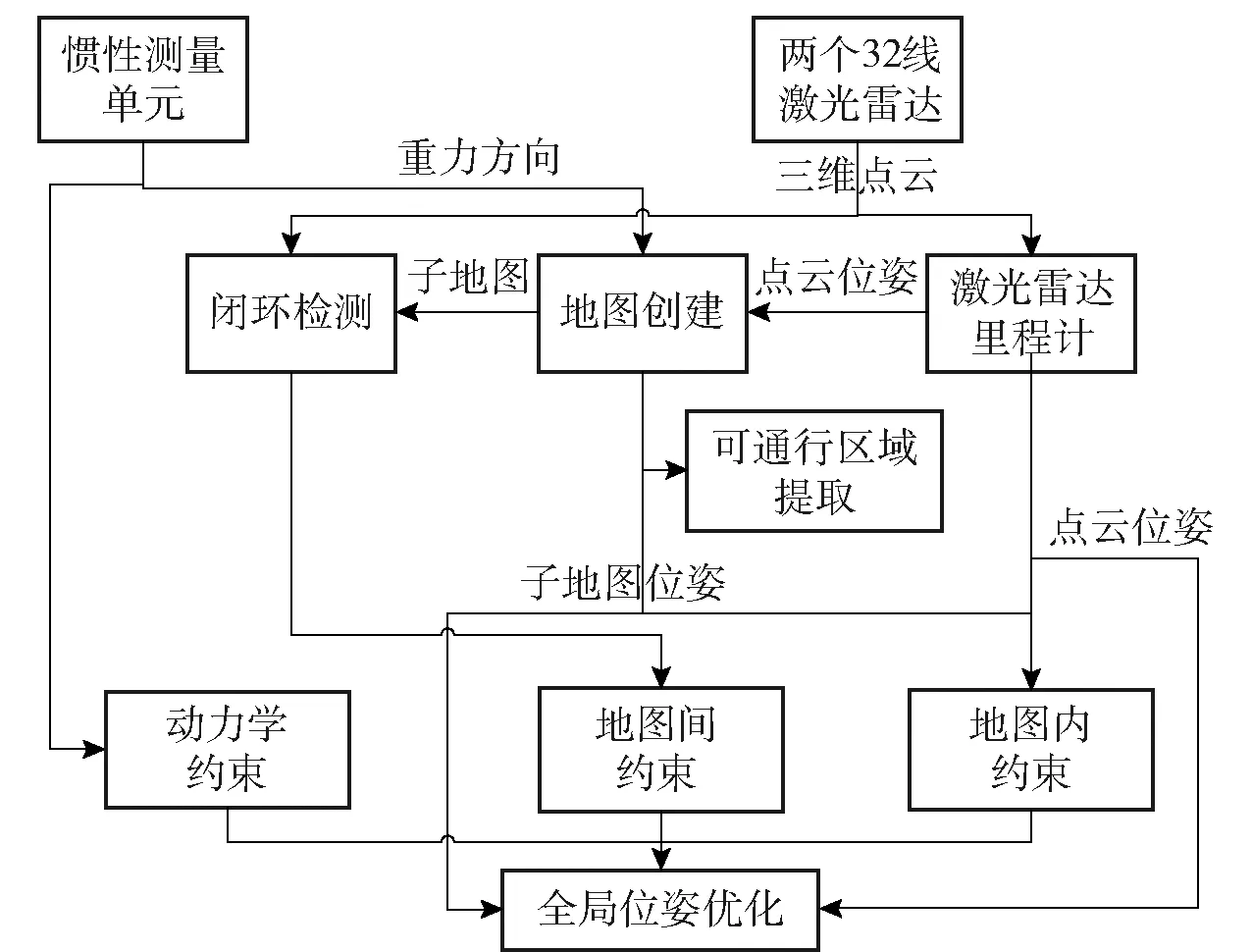
图1 实时6自由度激光雷达SLAM系统框架Fig.1 6-DoF lidar SLAM system framework

本文旨在基于无人平台实现一种适用于大尺度越野场景的实时SLAM系统。如图1所示，该SLAM系统框架分为两部分：三维地图构建以及6自由度全局姿态优化。来自IMU的线性加速度、角速度等信息以及来自两个32线激光雷达的点云共同作为该SLAM系统的输入。

为了实时进行地图更新，全局地图根据拓扑理论被分割成许多子地图，每个子地图都被认为是全局拓扑结构中的1个节点。实际上，子地图关联性形成了拓扑图中的边，最终获得一个完整的、结合了体素网格图和拓扑图优点的全局三维混合地图。为了保证地图切换时的平顺性，本系统同时维护具有一半重叠区域的两个子地图，并在倒数第2帧子地图基础上进行可通行区域提取，最终获得如图2所示可用于局部路径规划的可通行区域，图2中黑色区域代表未知区域，绿色区域代表可通行区域，白色区域代表障碍物区域，红色区域代表悬挂障碍区域，黄色圆点代表当前车辆位置，黄色矩形中心代表地图原点所在位置。

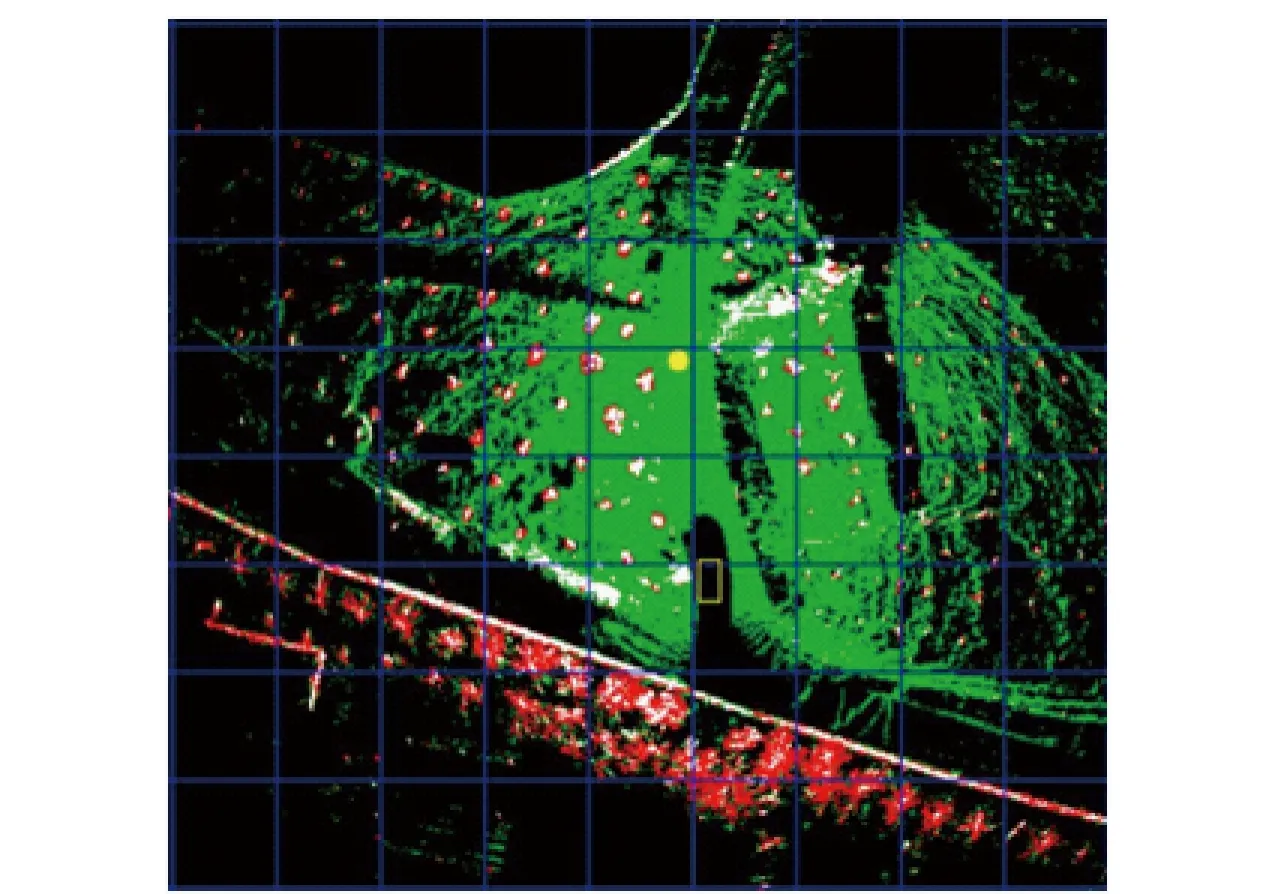
图2 可通行区域Fig.2 Transitable-area map

采用一种基于图论的SPA[3]优化方法处理SLAM中的6自由度全局姿态优化问题。稀疏位姿图将激光雷达位姿和子地图位姿作为待优化的位姿节点，位姿节点间的约束被分为三类：子地图间位姿约束、子地图内位姿约束以及动力学约束。最后采用Ceres求解器来计算优化函数。

2 三维地图创建

2.1 地图初始化

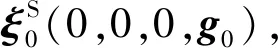
(1)

2.2 地图更新

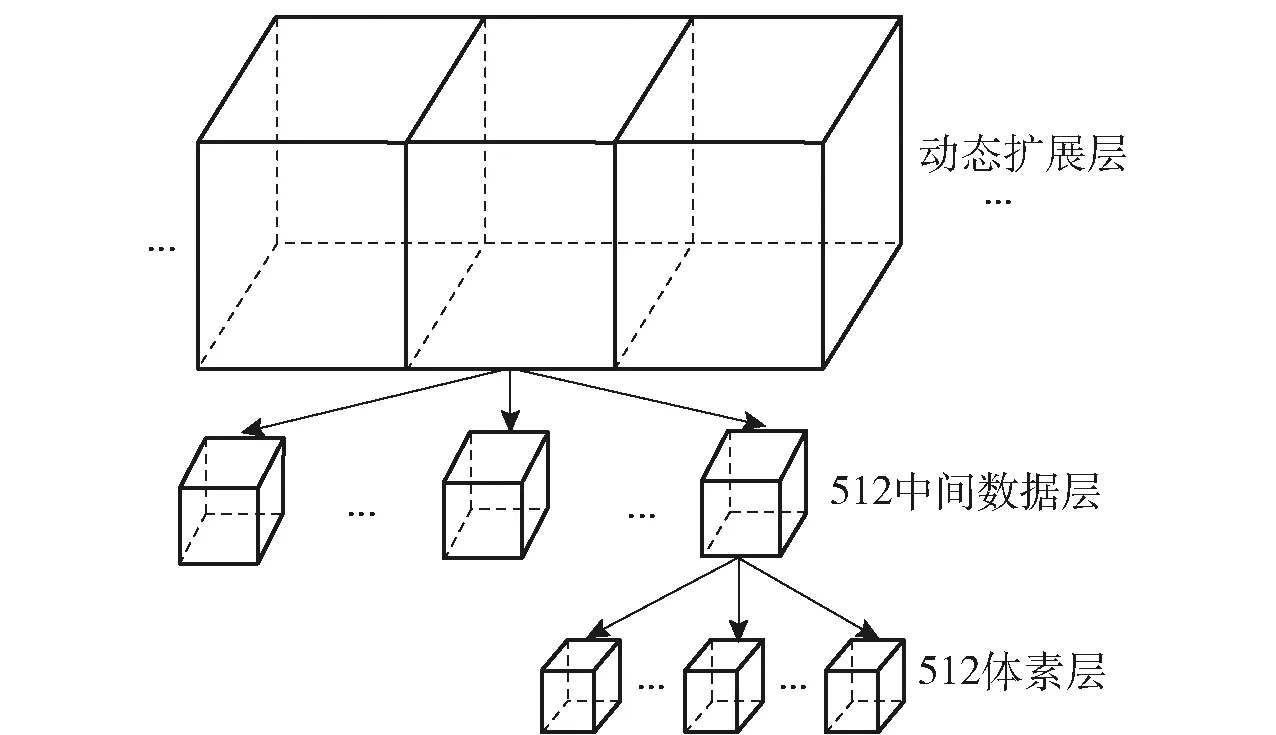
图3 子地图结构示意图Fig.3 Schematic diagram of submap structure

地图更新是一个反复将点云对齐到子地图坐标系下的迭代过程。当两帧相邻点云之间超过某一运动学阈值时，将雷达坐标系中的第1帧点云通过转换矩阵转换到子地图坐标系。子地图模型为三维概率体素地图，如图3所示。整个子地图的结构可以分为动态扩展层、中间数据层和体素层3层。动态扩展层中的元节点通过链结构进行管理，元节点数量随着环境观测的扩展而增加；元节点中的中间数据层节点和体素采用树形结构进行组织，每个元节点由512个中间数据层节点组成，每个中间数据层节点由512个体素组成。通过这种方式，链式结构高索引效率和树形结构高修改效率的优点被结合在一起。元节点的数量随着环境观测的扩展而增长。例如，当子地图的分辨率r即体素边长为0.1 m时，1个元节点可以表示6.4 m×6.4 m×6.4 m范围的环境。

2.3 可通行区域提取

(2)

式中：Zt为最大高度差阈值；ρt为体素密度阈值。

3 全局位姿优化

由于激光雷达里程计的积累误差，全局范围内的6自由度姿态将产生漂移，本文采用SPA方法进行全局位姿优化，从而减少累积误差。

3.1 闭环检测

闭环检测是消除累积误差的有效方法，识别观测过的历史场景是闭环检测的核心。在利用当前点云位姿与子地图原始位姿间的欧氏距离选取待检测子地图后[20]，本文将旋转直方图匹配(RHM)算法与迭代最近邻匹配(ICP)算法相结合，实现了一种RHM-ICP算法来实现实时的闭环检测。ICP算法用来计算当前帧点云与历史帧子地图之间的相对位姿ξ★，

(3)

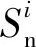
总之，在当前全面从严治党背景下，为了适应国家治理体系和治理能力现代化这一改革目标，作为党内监督的重要形式，在立足国情的基础上，纪检监察派驻制度改革也要顺应时代要求，实现组织理论、组织形式、组织人员、组织管理等方面的现代化，从而真正发挥“派”的权威，“驻”的优势。

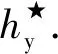
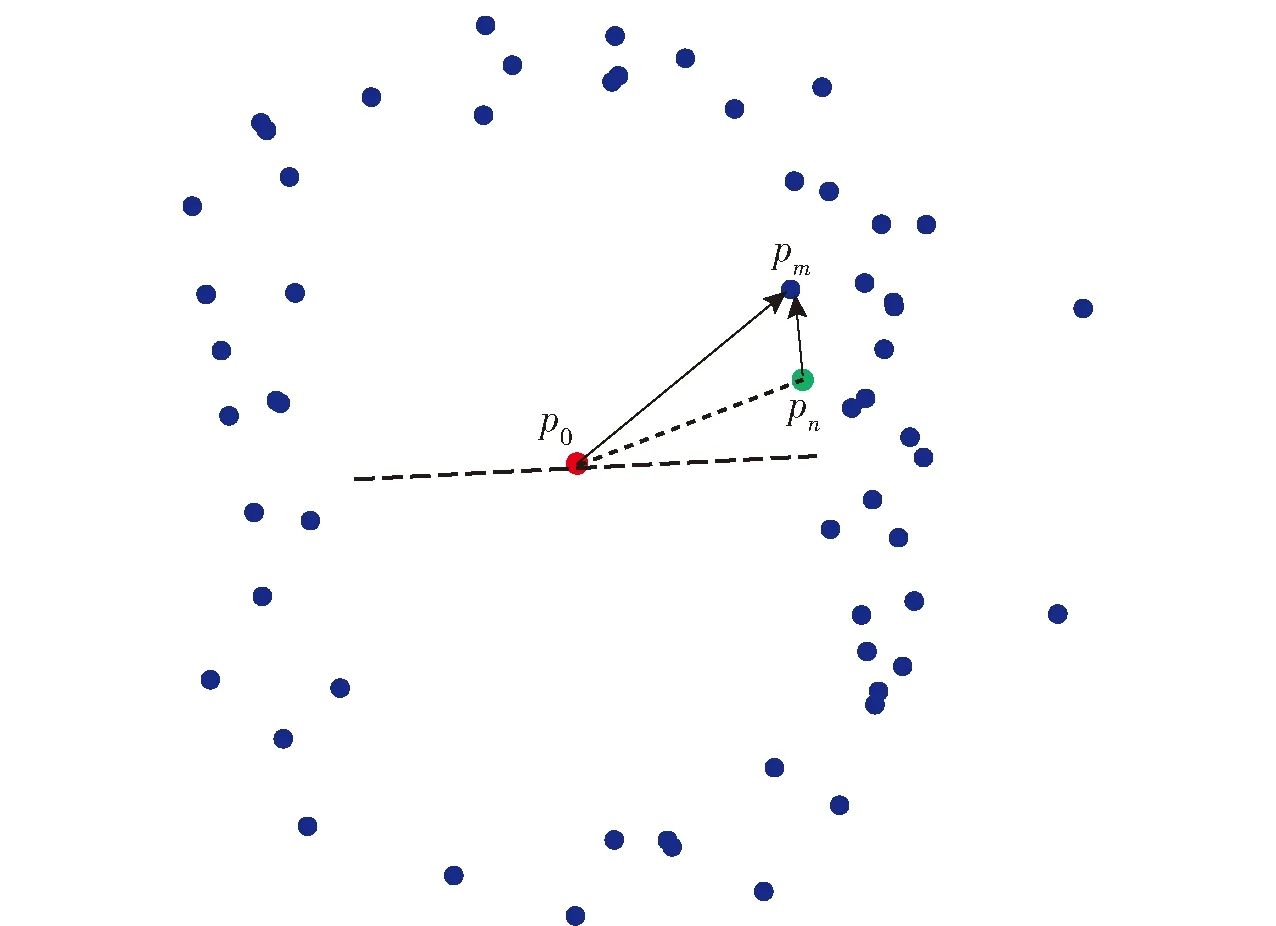
图4 旋转直方图匹配示意图Fig.4 Matching graph of rotation histogram

(4)

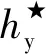
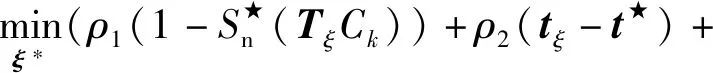
(5)

3.2 全局位姿优化

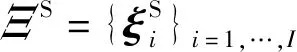
(6)

式中：ρ为权重系数；E为残差；Σij为协方差矩阵，由Ceres计算得到；约束ξij包含子地图间位姿约束和子地图内位姿约束。

对于动力学约束，本文计算如下问题：

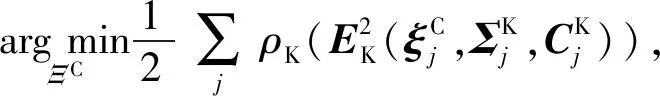
(7)

(8)

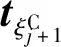
4 实验结果

本文在真实越野环境下进行了大量试验。图5所示为某实验场景(见图5(a))以及本文使用的实验平台(见图5(b))，图5中红色曲线根据实时动态差分全球定位系统(RTK-GPS)获得的数据绘制获得。在该实验路线中包括颠簸道路、匝道、岔路、混凝土路面和桥梁等多种地形。2台美国Velodyne公司生产的32线激光雷达安装在平台顶部两侧，以获得与实验场景相对应的点云，一个IMU被安装在平台的质心位置，用以实时测量无人平台的线性加速度和角速度。此外，还安装一部RTK-GPS用以获取平台的精确位置，并采用另一个高精度惯性导航系统(INS)获取参考姿态，以评估姿态优化性能。

图5 实验场景和平台Fig.5 Experimental scene and platform

4.1 三维地图创建及可通行区域提取

无人平台以20 km/h的平均速度运动，在三维地图创建过程中重建三维环境。图6所示为某越野实验环境中颠簸路面环境下该算法对于墙体、岔路口、桥、悬空障碍等进行三维地图创建以及可通行区域提取良好的结果。图6(c)、图6(f)、图6(i)中，黑色区域为未知区域，绿色区域为可通行区域，白色区域为障碍物区域，红色区域为悬空障碍区域，黄色圆点为当前车辆位置，黄色矩形框中心为可通行区域原点，蓝色网格为标尺线，网格的边长为10 m.图6(f)显示了对于树良好的悬空检测效果，正是由于悬空检测使得平台不会将树冠区域视为不可通行，从而保障了平台可以顺利通过此岔路口。

图6 天然地形、地图创建结果以及可通行区域提取结果Fig.6 Natural terrains,mapping results and transitable-area extraction results

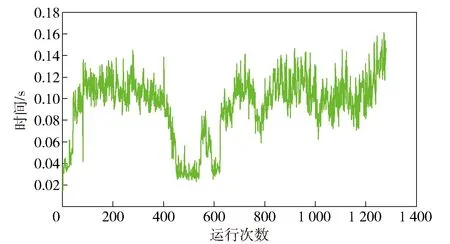
图7 地图创建及更新系统运行周期统计图Fig.7 Operational cycle of mapping and system updating

为了测量地图创建及更新系统的实时性，本文统计了从接收到点云数据到地图结果输出所用的时间，如图7所示。算法平均运行周期为(0.093 4±0.029 3)s，更新频率约为10 Hz，按最高行驶速度36 km/h计算，在一个运行周期内平台可运动(0.934±0.293)m，可基本满足无人平台日常行驶的需求。

4.2 全局位姿优化

本文在图5所示实际大尺度自然地形中评估了全局位姿优化的性能。图8所示为位姿优化结果中的位置优化结果。

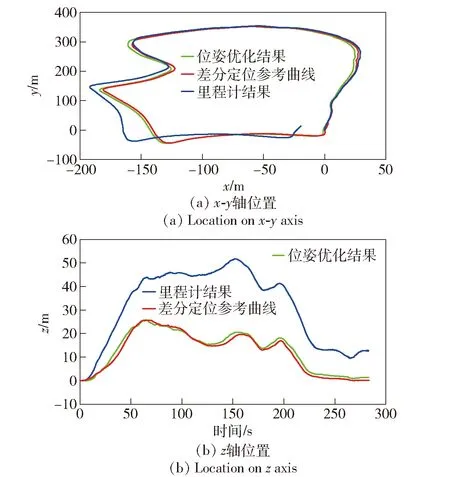
图8 位置优化结果图Fig.8 Optimized results of position

在某一1.5 km长环形路线上，当无人平台再次返回到起始位置时，累积的Oxy平面上误差达到21.5 m，并且z轴方向的累积误差在没有优化情况下达到9.5 m.在成功检测到闭环后，Oxy平面以及z轴方向的误差都被优化在1 m以内。从图8(a)中可以看到，在(25 m，250 m)处优化后的位置距离参考位置更远，这是全局位姿优化算法为了实现总体位姿误差最小而对局部位置精度的牺牲。

本文也对姿态优化性能进行了评估，结果如图9所示。从图9中可以看出，激光雷达里程计的姿态估计结果在局部范围内是准确的，但累积误差随着时间的推移而增加。当无人平台返回至起始位置时，累积航向角误差为9.0°，俯仰角误差为0.7°，侧倾角误差为2.2°.优化后的姿态与高精度INS测量结果几乎一致，不过在时间上稍有延迟。

为了评价闭环检测算法的实时性，本文将开源SLAM算法Cartographer以及基于NDT检测算法的闭环检测时间进行了对比，结果如表1所示。

从表1中可以看出，RHM-ICP闭环检测的时间最短，基本在0.4 s左右。由于NDT算法在闭环检测时需要迭代统计当前点云分布并计算概率，而RHM-ICP主要使用建图生成的概率栅格，无需另外计算概率，因此NDT算法实时性稍差；Cartographer算法实时性较差，这是因为其在进行闭环检测时没有对待检测的子地图进行筛选，导致待匹配的子地图随着平台运动不断增加，且由于实时性不够、容易造成计算量累积，从而进一步降低了闭环检测的实时性。

图9 姿态对比图Fig.9 Attitude contrast graph

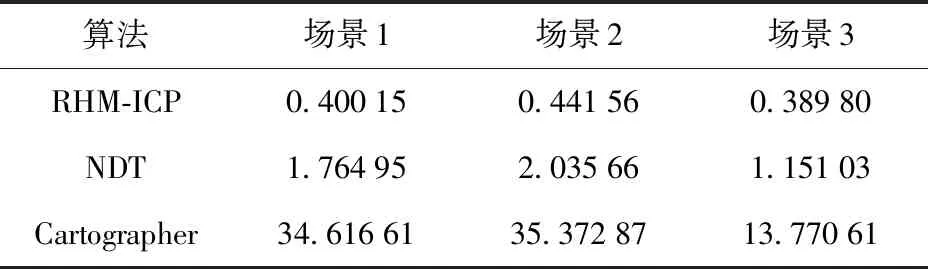
表1 闭环检测时间对比表Tab.1 Closed loop detection time table s

5 结论

本文提出了一种适用于大尺度越野环境的无人平台实时SLAM系统。通过三维地图创建获取了丰富的真实环境信息，在此基础上提取了可服务于无人平台路径规划的可通行区域；采用基于BBS的RHM-ICP算法实现了三维越野环境下实时的闭环检测；利用IMU添加动力学约束，通过SPA算法对6自由度全局位姿进行了优化。通过实验证明了三维地图创建和可通行区域提取良好的精确性和实时性，全局位姿优化使无人平台在GPS信号较弱甚至丢失时，可以获得精确的位姿信息。