潜航飞行体深水超音速气体射流的流动稳定性研究

张小圆，李世鹏，杨保雨，王勇，童悦，王宁飞

(1.北京理工大学 宇航学院，北京 100081;2.上海航天动力技术研究所，上海 201109)

0 引言

水下超音速气体射流是水下固体火箭推进系统工作中的典型物理过程，主要应用在潜基导弹、火箭助推深水鱼雷等水下航行体的推进系统中，同时也广泛存在于在水介质中工作的金属冶炼设备、气液喷射反应器、水下切割焊接设备等[1-2]。对于采用固体火箭发动机水下推进系统的研发，尾部射流的结构及发动机推力特性是决定整个潜航器水中弹道性能的重要影响因素[3]。发动机水下点火工作以后，在运动的航行体后端会形成一个不断充气的尾空泡。由于气体与水相互作用导致了空泡内气体压力变化，在内部压强与环境介质压差不规则变化作用下，空泡将产生不规律的膨胀或收缩运动，反馈到空泡内部则加剧了空泡内的气体压力脉动，该压强作用于航行器壁面，将与发动机推力一起产生脉动特性，对航行体弹道稳定性产生较大的影响。

目前，国内外学者已经做了大量有关水下气体射流的数值模拟和试验研究，但是相关研究集中在对于气体与水界面变化规律的预测和模拟，有关射流尾空泡脉动和推力不稳定性的具体机理尚有待进一步深入研究。在数值仿真探索方面，Labotz[4]、Ferguson[5]提出了球形气泡模型预测气体与水界面变化，该模型将气体与水界面理想地假定为只沿径向增长的球形模型，与实际结果存在较大的差异。贺小艳等[6]采用Level-set方法求解气体与水界面演化规律，并且主要针对初始气泡内的复杂波系变化进行仿真求解，得到了与试验相同的定性分析结果。Tang等[7]采用流体体积函数(VOF)多相流模型，分析了多相流流场结构对发动机推力的影响，认为射流过程中膨胀、胀鼓、颈缩或断裂以及回击4个过程是导致推力振荡的根本原因。甘晓松等[8]采用混合模型对有无来流的射流流场进行了模拟，发现有来流情况下射流不会产生断裂和回击现象，但没有对推力振荡进行更详细的分析。唐云龙等[9]对水下固体火箭发动机的推力进行了更进一步的分析，发现推力频谱呈现多阶频率峰值，其产生原因是多次胀鼓及回击破碎作用。

在试验方面，Loth等[10]比较了平面欠膨胀气体射流在空气中和水中的流场，观察到不同于空气中的衰减特性和湍流混合效果。从Shi等[11]对气体射流流场压力的测量结果来看，实际振荡过程更加复杂，包括由湍流引起的低幅高频压力、由胀鼓引起的中频压力以及由激波反馈造成的高幅低频压力。张孝石等[12]利用水洞试验及动态测力系统捕捉到了射流振荡诱导喷管口平面处主频为200 Hz的压力脉动。贾有军等[13]采用水下点火试车系统对高温燃气尾流进行观察，也发现尾流一直发生小幅振荡、间歇发生大幅振荡的特征。从工程实际应用来看，水下固体燃气推进系统在工作过程中存在着不稳定的特征，而燃气尾流的振荡对推力将产生直接影响。

根据现有文献结果分析，在水介质中，不论是常温气体射流还是高温固体燃气射流，都存在尾流振荡的特性，二者的基本流体动力学机理是相同的，都是气体与水相互影响产生的高度湍流混合过程。由于固体燃气射流操作和计算的复杂性，本文采用常温可压缩空气为射流气体进行研究，不考虑重浮力和两相之间的换热传质过程，重点针对流场的结构脉动特性进行研究。

多数学者采用雷诺平均湍流模型(RANS)对这一过程进行求解，得到的都是时间平均后的压力、速度、密度，不能够深入了解流场振荡机理。本文采用VOF多相流模型，结合k-ωSST和改进的延迟分离涡模拟(IDDES)方法进行平面二维超音速气体射流的数值模拟，并与水下射流试验结果进行对比，k为湍流动能，ω为湍流耗散比。通过对流场结构和物理参数变化的深入分析，得到了流场不稳定振荡的深入机理，相关研究结果可为水下固体超音速燃气射流的基本流动过程提供理论依据。

1 物理模型和计算方法

1.1 深水发射模型

本文主要研究深水(100～400 m)条件下，带有固壁发射装置的发动机在静水环境下气体射流的流场结构。仿真截取尾部喷管及固壁建立控制区域，具体尺寸参考高压试验水箱，如图1所示。计算域左右壁面距离为喷管出口直径的200倍，水域高度为喷管出口直径的400倍。

图1 几何模型Fig.1 Geometric model

1.2 控制方程及推力计算方法

本文采用VOF多相流模型结合k-ω剪切应力传输(SST)IDDES湍流模型进行平面二维超音速射流的数值模拟，控制方程包括质量守恒方程、动量守恒方程、能量守恒方程和体积输运方程，具体如下：

(1)

(2)

(3)

(4)

式中：ρ为密度；下标m代表混合相性质；ui、uj为速度分量；p为压力；μm为黏性系数；下标n为各单相性质，其中w代表水，g代表气体；α为各相体积分数；E为能量；keff为有效热传导系数；T为温度。

分离涡湍流模型(DES)最早由Spalart等[14]提出，其基本思想为在壁面边界层采用雷诺时均纳斯- 斯托克斯(N-S)方程求解，而在大量分离区采用大涡模拟亚格子模型求解。之后，由于存在网格引起的分离和对数层不匹配问题，Spalart等[15]和Shur等[16]提出了进一步完善的Delayed DES模型和Improved-DDES模型。2002年，Travin等[17]提出了针对k-ωSST的DES版本。该模型在飞机机翼、汽车外形空气动力仿真、水力机械以及超音速气体射流等多个领域的湍流仿真计算中取得了比RANS更精确的结果[18-20]。在气体与水两相流领域，Fronzeo等[21]考虑到气体与液体界面的强烈湍混，将该模型运用于气体与水两相流仿真，捕捉到更加符合试验结果的气体与水界面。本文所采用湍流模型为k-ωSST IDDES模型方程如下：

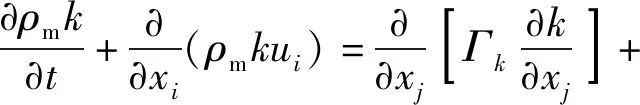
(5)

(6)

式中：Gk为k的产生项；Gω为ω的产生项；Yk和Yω为k、ω的耗散项；Dω为交叉扩散项；Sk和Sω为用户自定义源项；Γk和Γω为k、ω的有效扩散系数，Γk=μm+μt/σk，Γω=μm+μt/σω,σk和σω为k、ω的湍流普朗特数，μt为湍流黏性系数。

水下固体火箭发动机的推力计算方法与空气中工作的发动机一样，总推力为发动机内表面受力和外表面受力的合力，推力计算示意图如图2所示。图2中：pc为燃烧室压力；pa为水环境压力；pb为尾部背压；pj为喷管段压力；Ac、As、Ae分别为燃烧室壳体内部截面积、外部截面积和喷管出口面积；F为水下发动机推力。水下发动机由于前端面水环境压力pa和后端面的背压pb不同，会产生额外的压力推力项，而且尾壁面处背压受气体与水相互作用影响，有剧烈的压力振荡现象。因此，水下发动机的推力可以表示为前后表面压力差形成的合力与燃气的动量推力之和。本文中，采用压力积分求解喷管受力Fj和尾部壁面受力Fb.水下发动机推力F可表达为

(7)

式中：s1为图1中喷管壁面面积；s2为图1中尾部壁面面积。

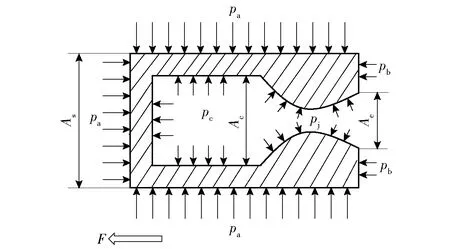
图2 固体火箭发动机推力示意图Fig.2 Thrust of solid rocket motor

1.3 计算网格与网格无关性验证

结合水下发动机的实际工作环境和深水高压试验舱尺寸，本文建立了Oxy平面二维模型，z轴方向默认为1个单位长度。计算域包括Laval喷管内流区域、尾部壁面和外部水介质射流区域。计算网格采用结构化网格，对喷管内流区以及射流中心核心区域进行加密。网格划分示意图如图3所示。图3中de为喷管出口直径。

图3 不同喷管出口壁面直径网格示意图Fig.3 Grids of different bottom diameters

为了排除网格对计算结果的影响，分别采用不同密度的网格(10.8万，15.6万，20.1万)进行网格无关性验证，得到喷管轴向无量纲归一化受力及同一时刻轴线压力分布如图4所示。图4(a)中：y轴为喷管轴向推力，通过Fj/(peAe)(pe为设计工况下喷管出口压强)进行无量纲并除以最大值归一化；x轴为无量纲化时间，通过tue/de(t为计算流动时间，ue为喷管出口速度)得到。图4(b)为相同时刻喷管轴线压力分布。由图4(b)可以看出，在不同网格密度条件下，流场变化规律基本相同。本文采用中等数量级网格进行计算，在确保计算精度的前提条件下可以减小运算所需资源。

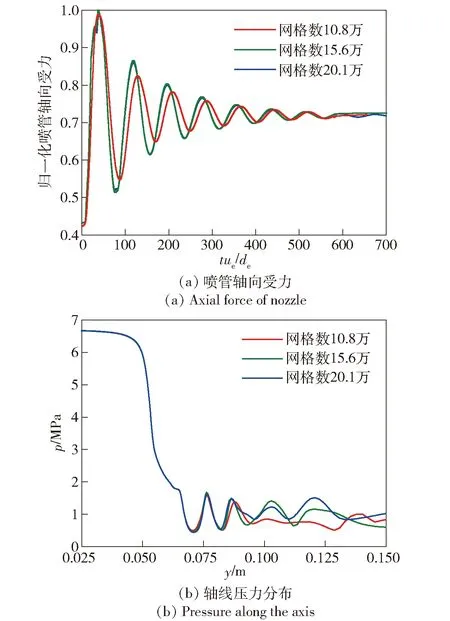
图4 网格无关性分析Fig.4 Mesh independence analysis

1.4 边界条件与仿真工况

计算介质材料采用空气和液体水，设水为主相，密度为998.2 kg/m3,空气为第2相，采用可压缩理想气体模型，常温条件下两相表面张力[18]设置为0.072 N/m.驻室入口和计算域出口采用压力边界条件，其余为无滑移固壁边界条件。采用深水环境压力对计算域进行初始化，喷管区域初始化为可压缩气体，压力为堵盖打开压力4 MPa.计算采用的参数和仿真工况如表1所示，分别设置不同水深(100 m，200 m，300 m，400 m)、不同喷管出口壁面直径(19.2de,38.4de,57.6de)仿真工况。

表1 仿真工况Tab.1 Simulation conditions

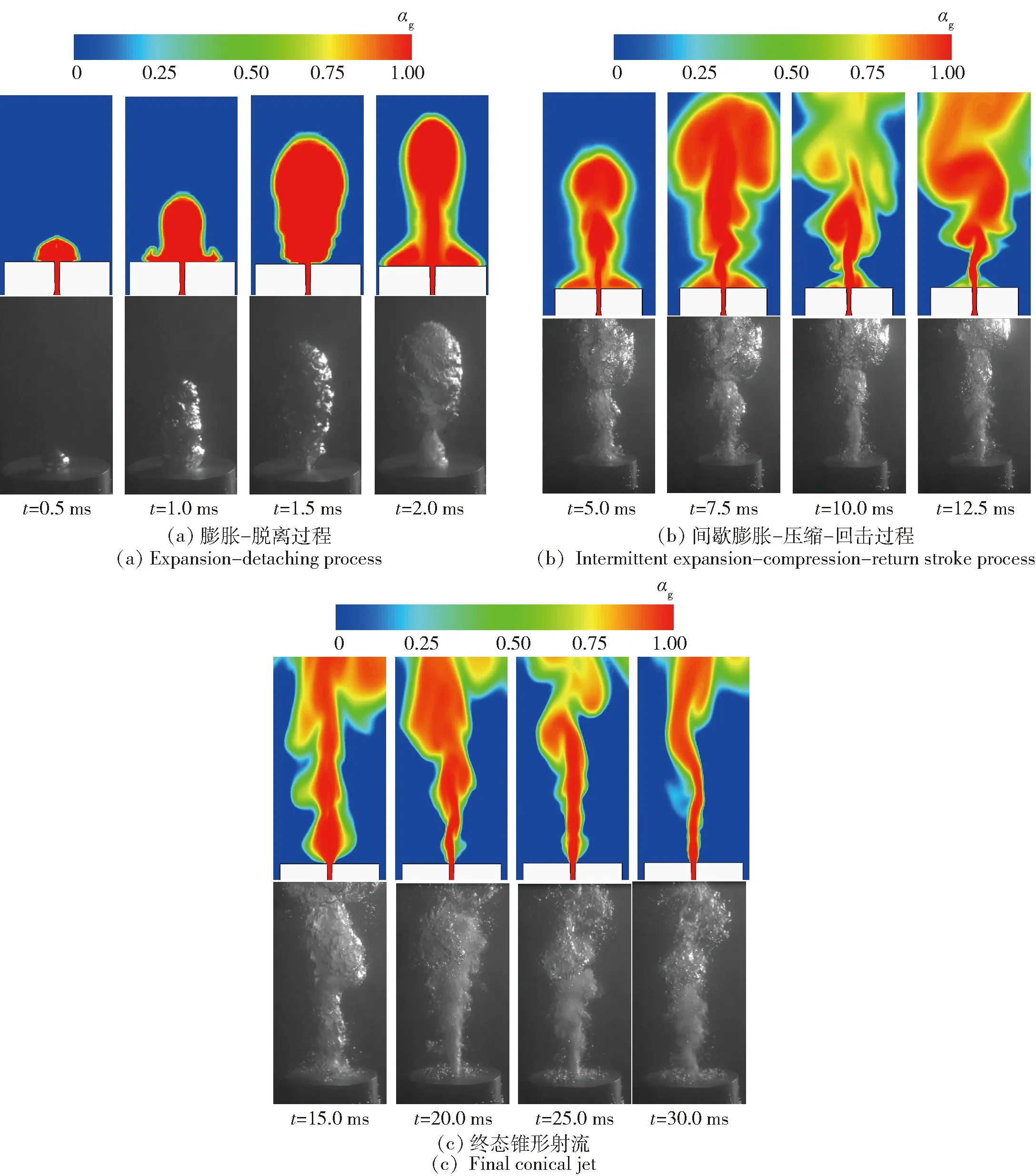
图5 100 m水深射流形貌拟序图(上为仿真结果，下为试验结果)Fig.5 Time-varying phase development in 100 m-depth water(upper:simulated results;below:experimental results)

2 计算结果分析

2.1 气体- 水介质两相形貌变化规律

2.1.1 水下气体射流仿真与试验结果

图5所示为100 m水深、19.2de尾部壁面面积仿真工况下水下气体射流的仿真结果和试验结果拟序图。从图5可见，气体从喷管喷出的形态变化经历了以下3个过程：1)膨胀- 脱离过程。气体从喷管喷出以后首先沿壁面扩张，占据一定直径范围尾部壁面位置后，射流气体开始向轴向膨胀，形成第1个气囊。然后气囊继续扩大、上升，从尾部壁面开始收拢，占据壁面的气体逐渐收缩，最终第1个气囊逐渐脱离尾部壁面。此时，从喷管出口到第1个气囊中部轴线已经形成完整的气体通路。该过程为射流初始阶段，持续约2～3 ms，在此阶段射流尾空泡结构刚开始成形，射流气体动量较大，受水介质阻碍衰减作用较小，射流形貌仍然保持良好的对称性。2)间歇膨胀- 压缩- 回击过程。第1个气囊脱离壁面后，气体沿通路仍然不断射入水中，部分气体继续沿尾部壁面膨胀，形成1个锥形气囊。此时锥形气囊中的气体并没有最开始那么多，气压不足以抵抗高背压，在惯性速度衰减后会被水介质环境压缩，形成回击过程，对尾部壁面产生冲击。然后射流重新累积气体开始膨胀，但由于气体被惯性不断带入下游气囊，在第1个气囊和喷管之间不断形成膨胀- 压缩- 回击现象，这个阶段明显的特点是喷管出口位置处有规律的胀鼓现象。3)终态锥形射流。最终随着气流的不断喷出，整个射流为不稳定的倒锥形，包括气体与液体界面的湍涡掺混、气泡溢出以及仍然存在的喷管出口附近中心气流不稳定间歇胀鼓现象。

2.1.2 射流形貌特点定量分析

为了定量化研究射流形貌特征及变化规律，定义射流高度和宽度如图6所示，喷管出口端面到最上部气体与液体边界垂直距离为射流高度H，射流最左侧气体与液体边界到最右侧气体与液体边界的水平距离为射流宽度W.射流颈部最上沿到尾部壁面的垂直距离为射流颈部长度Hn.

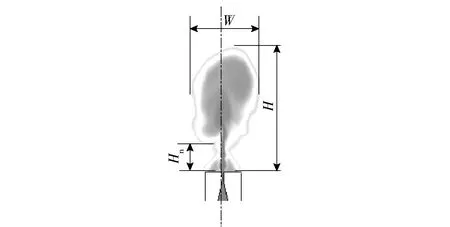
图6 射流形貌定义方式Fig.6 Definition of jet parameters

通过对仿真结果云图和试验结果提取边界轮廓和坐标，得到初始阶段(35 ms)水深100 m时射流高度和宽度对比结果如图7所示，从而验证了仿真模型及其合理性。

图7 计算结果与试验结果对比曲线Fig.7 Comparison of calculated and experimental results

在初始阶段时间范围内，射流高度和宽度在不同水深条件下的变化规律如图8和图9所示。从图8和图9可以看出：在不同的水深条件下，射流高度和宽度随时间都在增长，射流高度随时间的变化较为规律，开始增加较快，之后增加量逐渐减少；射流宽度在起始阶段也有较大的增加，之后增加较为缓慢。这是因为射流起始动量很大，受水介质影响较小，会以一定速度冲向水环境介质，破坏整个静态水环境的平衡；而在壁面效应作用下，射流气体会首先沿壁面进行扩展，之后才沿轴线方向膨胀。随着气体的不断喷出，在水介质作用下，射流速度衰减，整个气囊膨胀受到约束，高度和宽度增长也逐渐变得缓慢。

图8 不同水深射流高度、射流宽度随时间变化规律Fig.8 Jet height and width vs.time in different water depths

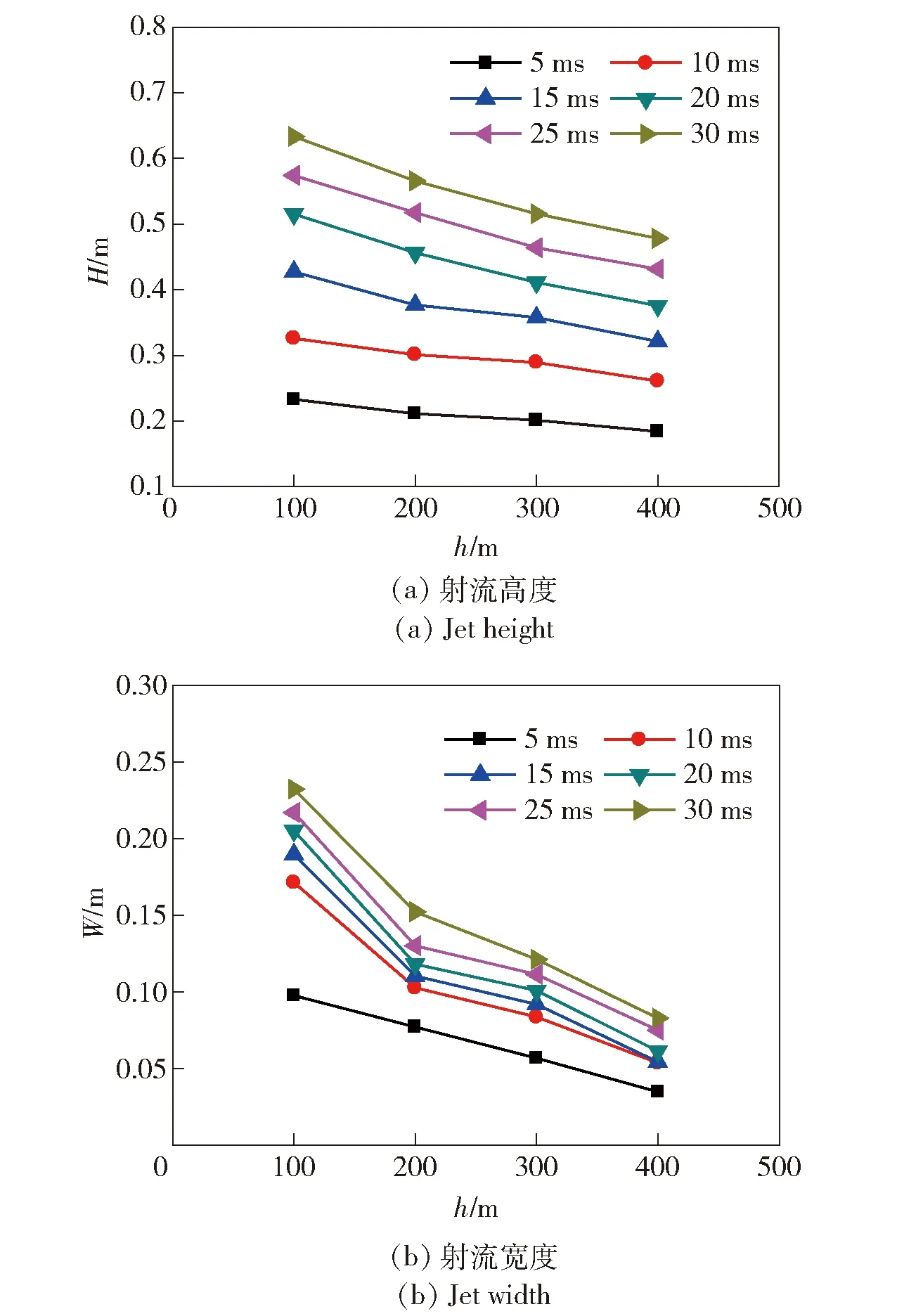
图9 不同时间射流高度、射流宽度随水深变化规律Fig.9 Jet height and width vs.water depth at different times

在不同时刻，射流高度随着水深的增加呈线性减小；射流宽度随水深呈非线性减小，随着水深的增加，射流宽度减小的越来越缓慢。这是因为在100 m水深条件下，水环境背压较小，射流处于欠膨胀工况下，射流宽度较宽。而在200～400 m工况，水环境背压增大，射流工作在过膨胀状态，射流宽度较窄，过膨胀压力比越小，射流形貌越窄，即喷管设计出口压强与环境压强之比减小，射流排出的气体膨胀要克服更大的外界阻力，因此整体形貌变得更加细短。

在初始阶段，发动机尾部壁面直径的变化对射流形貌的影响如图10所示。由图10可见，3种不同尾部壁面直径条件下，射流高度和宽度曲线几乎重叠。这是因为在3种不同尾部壁面条件下喷管参数相同，出口压强和环境背压也相同，射流形貌结构将会保持原貌。

图10 射流高度和射流宽度随出口壁面直径变化规律Fig.10 Changing curves of jet height and width with different nozzle exit diameter

通过对气体- 水介质两相形貌变化规律的分析可知，射流整体形貌与介质水的背压关系最大，不同水深条件下，射流形貌会出现明显变化。尾部壁面直径的变化对射流形貌几乎没有影响。

2.1.3 射流两相边界不稳定分析

图11 射流左右边界和宽度与高度比随水深变化规律Fig.11 Change of jet boundary and ratio of width to height

为了反映射流形貌在整个过程中的不稳定特性，计算得到左右最大宽度变化以及宽度和高度比变化如图11所示。从图11中可以看出，射流左右边界随时间的增长并不是完全对称的，左右两边的最大宽度会呈现交叉变化。射流宽度与高度的比值出现先增加后减小的变化趋势，射流在初始阶段沿周向膨胀较迅速，稳定之后射流宽度变化较小；而气体主要由轴向射入介质水，射流表现为不稳定倒锥形(见图5)。

图12 射流剪切不稳定Fig.12 Shear instability of jet

气体与水介质的速度剪切作用，以及尾流核心气体内部的不稳定性将对射流边界变化产生综合影响，导致射流气体与水界面产生胀鼓及不稳定湍混，如图12所示。从图5的试验结果也可以看出，射流左右气体与水边界会出现不同程度的湍混现象，根据两相Kelvin-Helmholtz不稳定性线性增长理论[22-23]，当两相射流界面存在速度间断面时，该间断面是不稳定的；初期扰动呈线性增长，形成胀鼓。小扰动在界面增长率c为

(8)

式中：a为波数，a=2π/λ，λ为扰动波波长；σ为界面张力；vg为气相速度；vw为液相速度；g为重力加速度。根据线性稳定性结论分析可知，扰动增长率随两相速度差的增加而增加，随界面张力的增大而减小。

在气体与水相互作用的过程中，由于气体内部流场会受到水介质不同程度的阻碍衰减影响，可看作不稳定速度扰动源，该扰动逐渐发展将使得气体与水界面先出现胀鼓，然后进一步发展为卷吸掺混，最终气体与液体边界会产生动态不稳定的湍流混合现象。

2.2 尾流场参数振荡分析

2.2.1 欠/过膨胀条件下尾流场特性

在气体开始喷出后，由于底部空间封闭，压力出现了较大的上升波动。在气体向尾部壁面扩张、轴向膨胀后，中间气体通路及波系初步建立，整个气囊上边缘与水环境产生了较大的压力冲击，此时气囊内的压力小于环境背压，如图13所示。从图13中可以看出，从马赫数分布来看，中间气体通路速度最大，沿轴线从出口到上部气囊中间形成了喷管出口射流激波系；在水环境高背压作用下，速度很快衰减，气囊边缘部分出现了向下回流，气囊内形成了自上而下的自旋涡。此时整个流场还保持对称性和稳定性，压力、速度分布及气体分数等高线。从图13中还可以看出，射流处于欠膨胀和过膨胀状态时，气体与水界面影响范围会有所不同，欠膨胀工况下射流形貌表现出更加明显的颈缩效应。与空气介质射流气体的出口波系[24]相比，内部气体速度衰减明显，由颈缩部位分成两部分，下半部表现出射流衰减特性，上半部气囊内速度有二次上升，整个尾部流场由颈缩位置处分为特征不同的两部分，如图14所示。

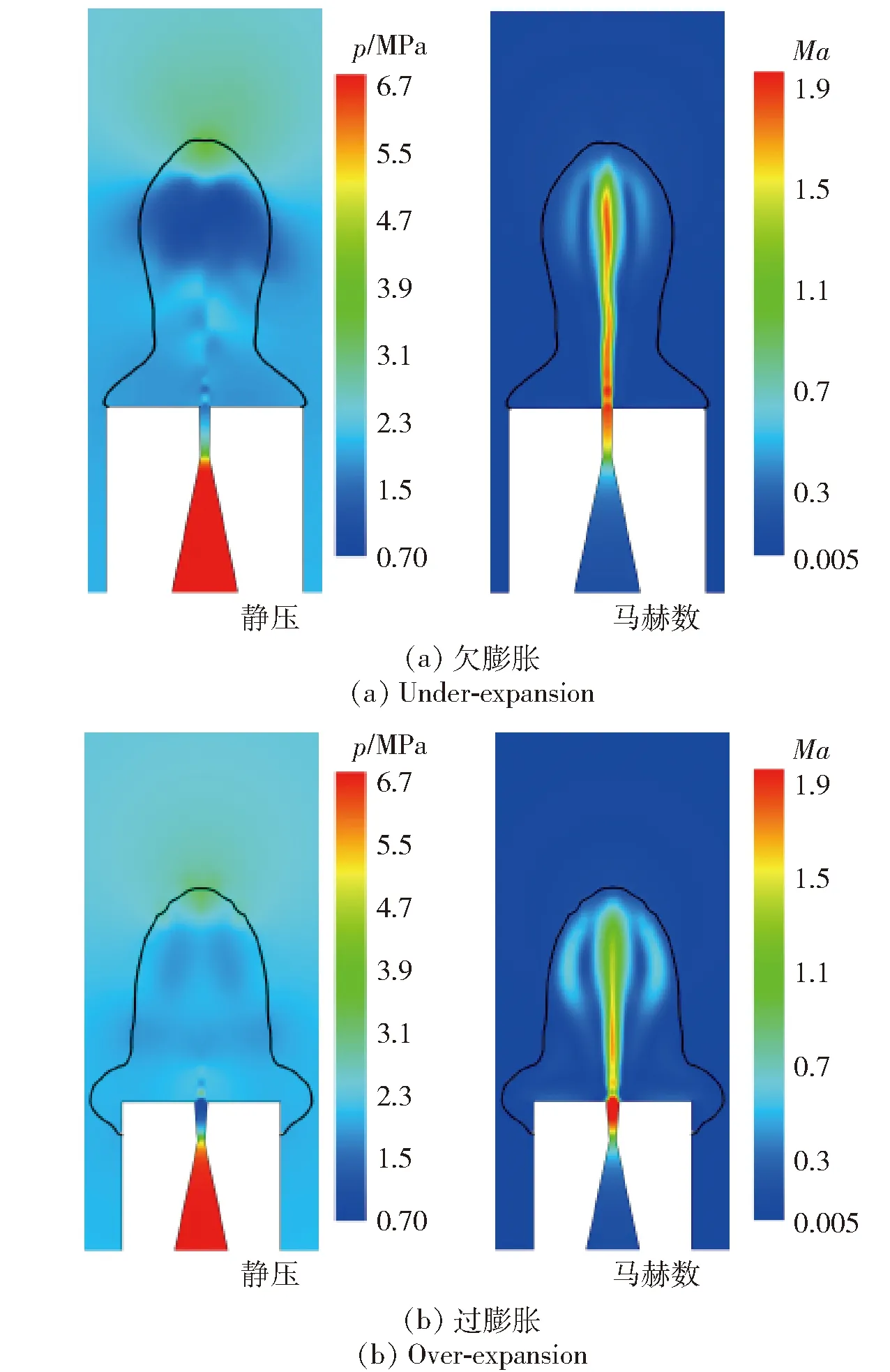
图13 初始对称流场静压(左)和马赫数(右)分布图Fig.13 Initial pressure (left)and Mach number (right)distribution

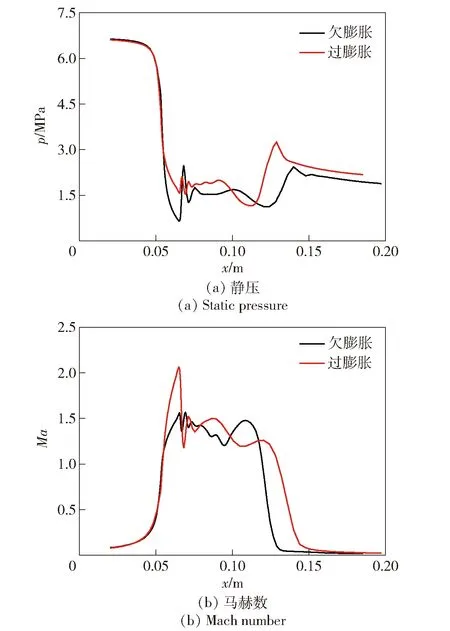
图14 射流尾部轴线静压和马赫数分布曲线Fig.14 Static pressure and Mach number in jet wake

从图5的仿真和试验结果可以看出，射流形貌有明显的颈缩形态，从颈部可以将射流划分为上部气囊和下部锥形体两部分。其中锥形体内射流动量较大，中心有完整的气体动态衰减波系，该部位气体流场状态会影响尾部壁面处的压力分布，从而造成对推力的影响。上部气囊内气体动量由于外部介质阻力已经衰减，但是上游气体的加速作用会形成二次加速，颈部收缩部位是整个形态的分界点，由于射流颈缩位置左右不对称，选取左侧颈部位置进行分析，可以得到初始阶段颈部长度随时间的变化如图15所示。由图15可见，颈部位置在初始时刻会有较大波动，由于衰减不均匀及气体再次膨胀，颈部位置会有明显移动，后期随着射流逐渐喷出，颈部位置上移，依然有较大波动。

图15 颈部长度变化Fig.15 Length of jet neck

从图5射流形貌拟序结果来看，颈部位置以下，射流会发生周期性胀鼓现象，表现出极大的不稳定性。这种不稳定性与中心气体内部结构波系的不稳定运动和破坏重建密切相关。

随着第1个气囊的上升，气囊内压力和速度逐渐出现不对称衰减，形成的激波系也被破坏。表2所示为一次完整的波系破坏重建过程。由表2可见，该阶段整个射流流场表现出了极大的不稳定性，出口激波系不断重建，在喷管出口表现出射流多次胀鼓现象。

2.2.2 尾流场振荡定量分析

为了能够定量测量这种不稳定性产生的振荡频率，在喷管出口位置及出口附近轴向和径向设置监测点，监测点位置如图16所示，喷管出口位置轴线中心监测点为P00，沿轴线方向分别在距离尾部端面de、3de、5de、7de、9de、14de、34de共7个位置设置监测点，分别为P10～P70；同时在尾部壁面一侧及同位置处壁面设置5个监测点，分别为P11～P15.对流场参数随时间的变化进行监测，采样间隔为1×10-5s.为了更好地分析尾部喷管流场的周期振荡特性，下面进一步对仿真得到的压力- 时间信号进行快速傅里叶变换(FFT)，分析其振荡频率和幅值特点。

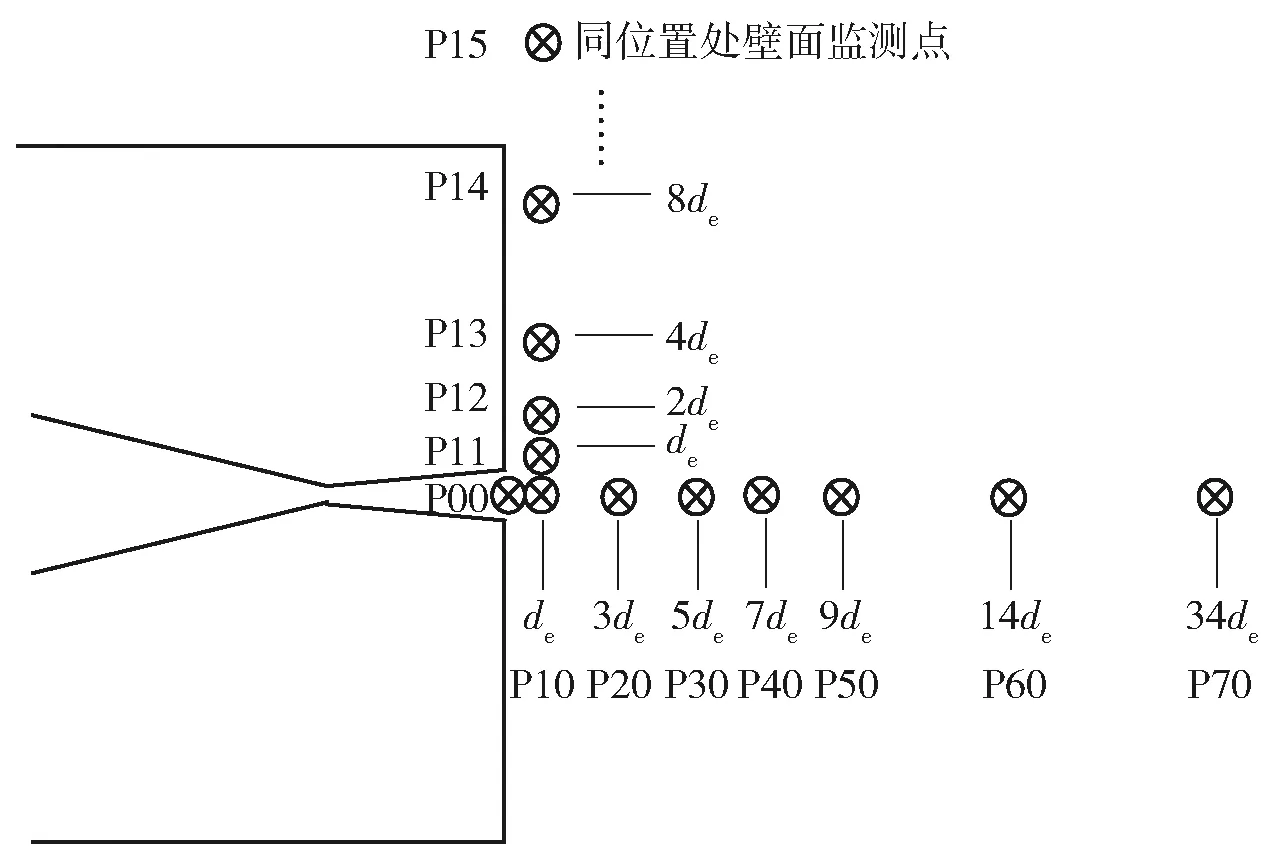
图16 监测点示意图Fig.16 Monitoring points distribution

监测得到的轴线方向和径向方向压力时域和频域变化如图17所示，轴向数据为发动机中心轴线上8个点(包括喷管出口位置处监测点)的压力监控采样数据，径向方向为最靠近壁面层监测点压力数据。从图17(a)、图17(b)中可以明显看到，当射流从喷管喷出建立相对稳态的射流流场后，轴线和壁面径向监测点流场压力信号会出现周期性脉冲峰值，同时伴随着高频低幅快速波动。从图17(c)、图17(d)的频谱分析结果图来看，尾部轴向和径向压力频率带宽主要分布在0～10 000 Hz；压力峰值主频率分布在600～800 Hz.这里的压力大幅度振荡来源于尾部气体通路内激波系的不稳定运动以及失稳重建，这种激波反馈不仅导致了气体与液体界面的周期性胀鼓膨胀，而且在喷管出口产生了强烈的涡旋湍混现象(见图5)。

表2 尾部激波波系
Tab.2 Shock waves in jet tail

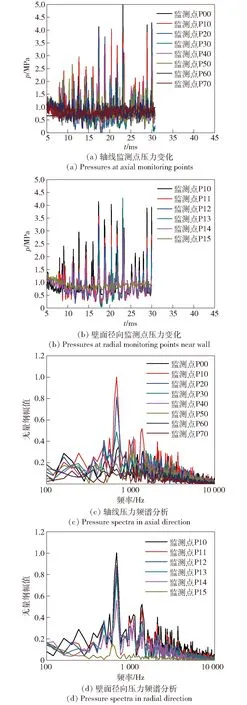
图17 压力监测信号时域和频域分析Fig.17 Time and frequency domains of pressure signals

不同喷管出口底部直径条件下，出口位置附近监测点压力频谱分析如图18和图19所示。由图18和图19可以得到，当水深由100 m增大到400 m时，尾部压力扰动表现为频率和幅值增大，这是因为射流在深水条件下所处工况为过膨胀工况，射流在较大背压作用下表现出更大的不稳定性。随着出口壁面直径的增大，尾部压力扰动频率和不同位置处的振荡幅值也在增大。由于底部直径增大、尾部空间相对减小，射流气体与水相互扰动在小范围空间内表现出更高幅高频的特性。而径向不同位置处振荡幅值也不相同，中心气体内幅值较小、气体与水边界处幅值相对较大，远离出口的水介质处幅值又减小。

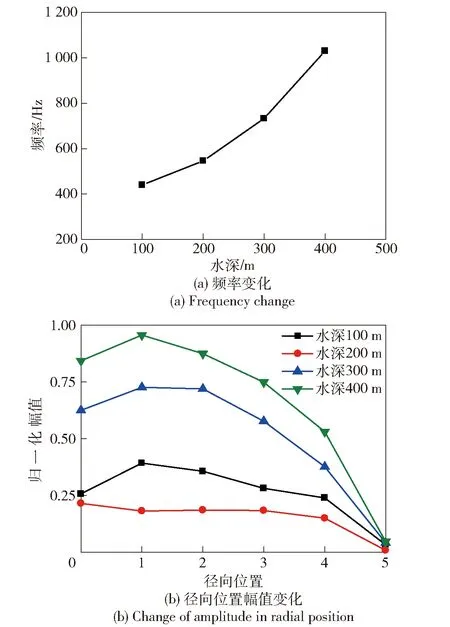
图18 不同水深流场振荡分析Fig.18 Oscillation of flow field in different water depths

图19 不同喷管出口壁面直径振荡分析Fig.19 Oscillation in diameter of wall at the mozzle exit

2.3 推力分析

在不同水深和不同喷管出口壁面直径条件下，发动机推力变化曲线如图20所示。图20中：y轴为无量纲化推力，通过F/(peAe)得到；x轴为无量纲化时间，通过tue/de得到。从图20中可以看出，初始阶段发动机会产生较大的推力峰值，之后逐渐趋于稳态并伴随较大的压力振荡。这是因为射流气体喷出瞬间与外部介质水有较大的压力冲击作用(见图13)，该冲击作用在喷管出口壁面上会形成附加推力。在不同水深条件下，水深越深，初始峰值越大；在不同出口壁面直径条件下，出口壁面直径越大，推力初始峰值越大。当射流状态趋于稳定后，推力也逐渐趋于稳态，并伴随较大的振荡波动。在本文研究的所有工况中均有较明显的推力稳态振荡现象。

2.4 推力振荡与尾流场振荡相关性分析

根据推力计算公式，可以得到不同水深和不同尾壁面直径条件下喷管壁面和尾部壁面的压力积分项变化，结果如表3所示。由表3可以看出，喷管受力在初始振荡收敛后逐渐趋于稳态值，在深水过膨胀工况下，喷管激波会被压入喷管段产生微小振荡。尾壁面初始压力的巨大变化是导致初始推力峰值的主要因素，同时喷管受力趋于稳态后，尾壁面推力项开始稳态振荡，此时振荡主要受尾部空间内流场压力振荡的影响。当水深增大时，尾壁面推力项振荡幅值增大、频率增高；当出口壁面直径增大时，尾壁面推力项振荡幅值增大、频率增高。

3 结论

本文通过分离涡湍流模型研究了水下固体火箭发动机气体射流尾空泡流场的流场结构和气体与水界面变化规律，分析了尾部空间内流场振荡特性及推力不稳定性产生的流动机理，同时针对该振荡特性对水下发动机推力的影响进行了分析和讨论。得到主要结论如下：

1)水下固体火箭发动机气体射流流场结构受外部水介质影响较大。超音速射流气体受到水介质的阻碍作用，会导致不稳定的衰减，从而影响射流的对称性，产生左右不同的形貌特征。具体表现在尾空泡气囊不对称、颈缩位置不对称以及尾部壁面气体分布不对称。当水深增大时，射流高度和射流宽度均明显减小。随着气体喷出时间的增加，射流径向和轴向增加越来越缓慢，且经历一定时间后射流径向基本不再增加，主要沿轴向扩张。

2)颈部以下锥形射流气泡会出现多次胀鼓现象，造成这种周期性胀鼓现象的内在机理是水环境下压强和速度衰减不均匀导致射流气体中心区激波系不断破坏重建，进一步影响气体与水边界湍混，形成胀鼓现象。胀鼓不稳定性产生尾流场的振荡频率约为600～800 Hz.

3)发动机推力在初始时刻会有较大的脉冲峰值，与初始时刻气体与水界面剧烈的冲击关系密切，之后逐渐趋于平缓，同时伴随着较强烈的高幅低频特征信号，这与尾流场的压力高幅脉动紧密相关。水深越深，喷管出口壁面直径越大，发动机推力振荡会越剧烈。