基于镀层界面剪切疲劳损伤的枪管寿命预测研究

2020-01-08耿雪浩周克栋赫雷冯国铜李峻松

兵工学报 2019年12期

耿雪浩,周克栋,赫雷,冯国铜,李峻松

(1.南京理工大学机械工程学院，江苏南京 210094；2.苏州工业职业技术学院精密制造工程系，江苏苏州 215000；3.中国兵器工业第208研究所,北京 102202)

0 引言

枪管是自动武器的关重构件，枪管寿终的主导因素是内膛的损伤累积，即射击过程中热、机械和化学综合作用的结果，其中热起主导作用[1]。射击时枪管的内膛损伤始于镀层破坏，在射击时的循环热冲击作用下，枪管镀层会发生岛状开裂，完整性遭到破坏，开裂后镀层在界面剪切作用下发生剪切破坏、失效剥落，使得基体材料直接暴露于高温火药燃气环境中，进而引发基体快速烧蚀、导致枪管寿终。研究发现，一旦镀层完整性遭到破坏，带镀层的身管烧蚀速度甚至要比没有镀层的身管更快[2]。

枪管寿命是困扰轻武器行业几十年的难题，也是国内外兵器行业上百年来持续不断、至今仍在研究的热点问题，国内外学者针对身管寿命已经开展了大量研究。沈超等基于有限元法和寿命试验结果，研究了某大口径机枪枪管内膛损伤情况对内弹道性能和弹头出膛状态的影响[3]；乔自平等通过对大口径机枪枪管失效规律的分析，研究了基体材料的烧蚀规律[4]；齐玉辉等研究了射击规范及典型使用条件对大口径机枪枪管寿命的影响[5]。对于枪管寿命预测的研究，目前已经发展出多种预测模型[6-8]。徐宁等提出基于镀层和基体结合部疲劳损伤累积的枪管寿命预测方法[9]，预测模型中计算载荷采用以压应力为主的Von Mises应力，材料抗拉强度采用的是常温数据。

本文根据身管镀层剪切失效理论和疲劳损伤累积理论，采用随温度变化的枪管材料抗拉强度，研究了某5.8 mm小口径步枪枪管在瞬态热压耦合载荷作用下，基于镀层界面剪切疲劳损伤的枪管寿命预测方法，为枪管寿命预测提供了新的途径。

1 镀层界面剪切损伤理论

镀层的损伤失效过程大致可分为开裂和剥落两个阶段。镀层的初始裂纹可能在身管进行第1次射击之前就已经存在，例如电解沉积铬在沉积及热处理去氢过程中产生的残余应力会导致镀层内部产生微裂纹[10]。射击时，镀层在瞬态高温热冲击作用下发生压缩屈服，然后在冷却过程中受残余拉应力作用发生脆性开裂。通过实弹试验发现,身管镀层表面在射击几十发甚至几发后便会形成大量宏观裂纹，而镀层开裂并不会立即导致身管失效,后期界面破坏导致的镀层剥落才会对身管寿命产生重要影响。镀层界面破坏也是一个长时间过程，镀层开裂后仍然能承受成千上万次循环热载荷的冲击，因此有理由认为镀层界面破坏是一个损伤累积过程，镀层剥落是循环热冲击作用下的疲劳行为。

对于开裂后的镀层剥落机制，Underwood在对剪切失效、弯曲失效和界面裂纹扩展失效几种身管镀层可能存在的失效模式进行对比分析后认为，镀层与基体界面附近的剪切应力是镀层界面破坏的主要驱动力，界面剪切失效是最有可能的镀层最终失效机制[11]。

图1所示为根据剪切失效理论绘制的枪管横剖面镀层受力分析示意图。图1中，b为镀层片段宽度，L为镀层片段长度，h为镀层厚度，τ为镀层片段底部切应力，Sc为镀层内部周向正应力。由图1可见，该镀层片段左侧存在一条张开型裂纹，右侧存在一条闭合型裂纹。射击时镀层片段右侧受热与压耦合下周向正应力作用，镀层所受热压耦合应力可表示为

Sc=St+Sp，

(1)

式中：St为热作用在镀层内产生的瞬态热应力；Sp为镀层受膛压作用产生的应力。

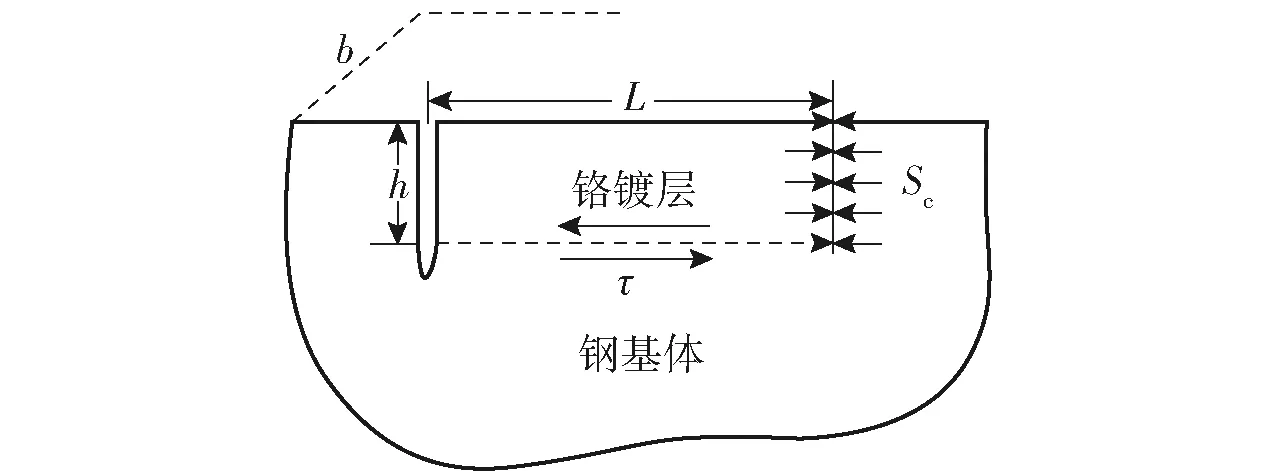
图1 枪管镀层剪切失效模型Fig.1 Shear failure model of coating on gun barrel

为简化计算，假设镀层片段内的正应力Sc沿镀层厚度方向均布载荷，以镀层半厚处的瞬态热应力和膛压作用应力代替镀层内平均热应力和平均膛压作用应力。瞬态热应力St在枪管周向上表现为压应力，可表示[12]为

St=Eα[Th/2-T2h]/(1-ν)，

(2)

式中：E为镀层的弹性模量；α为镀层的热膨胀系数；Th/2为镀层半厚处温度；T2h为2倍镀层厚度处温度；ν为泊松比。

假设枪管内壁薄层内的裂纹分布对膛压作用应力分布无影响，枪管内壁薄层的膛压作用应力与无缺陷厚壁圆筒在内压作用下的周向应力分布一致，则Sp可由著名的Lame公式确定，其在枪管周向主要表现为拉应力，

(3)

式中：p为膛压；r0和R分别为枪管内半径和外半径；r为枪管壁中某点距枪管对称轴的距离。

考虑到射击过程中枪管内壁应力以热应力为主，为表示及计算方便，假设压应力方向为正、拉应力方向为负，故射击时镀层片段内平均热压耦合应力可表示为

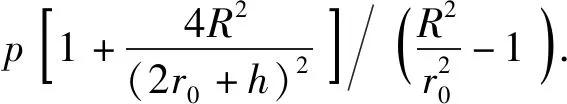
(4)

根据Evans等的界面失配力平衡概念[13],当镀层片段内产生周向力后，其底部会产生剪切力以平衡周向力，力平衡公式可表示为

τbL=Scbh，

(5)

消元移项后，得

(6)

因此bL表示镀层底部的受剪切力作用的面积，bh表示镀层侧面受周向力作用的面积。

联立(4)式和(6)式，镀层片段底部的剪切应力可表示为

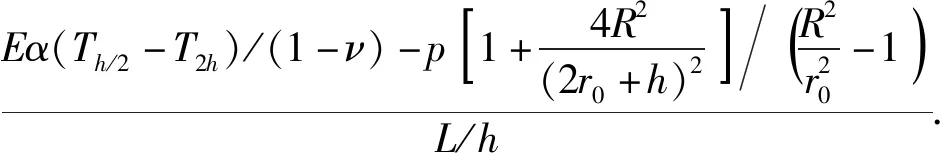
(7)

2 枪管寿命预测模型

2.1 疲劳方程

射击过程中枪管镀层与基体界面的疲劳可以看做热压耦合作用下的低周疲劳，其疲劳寿命可以利用Manson-Coffin疲劳方程[14]及修正后的Morrow方程[15]计算得出。当平均应力σm≠0以及平均应变εm≠0时，枪管镀层与基体界面疲劳损伤寿命计算模型为

(8)

式中：Δε为应变幅；σf为材料疲劳强度系数，σf=σb+350 MPa，σb为材料抗拉强度；N为枪管寿命；b′为疲劳强度指数，研究认为b′=-0.12时寿命估算结果较为谨慎；εf为材料疲劳延性系数，εf=ln(1-ψ)-1，ψ为材料断面收缩率；a为材料的疲劳延性指数，取值范围为-0.8～-0.3.

不同于单调加载情况，低周循环加载下材料会产生循环硬化或软化，其循环应力与应变关系会随循环数而改变，但达到一定循环次数后，材料对变形的抵抗能力会趋于稳定。由于循环稳定阶段是疲劳寿命的主要阶段，一般以稳定的循环应力与应变曲线表示材料的循环应力和应变性质，材料的循环应力与应变关系可表示为

(9)

式中：Δσ为应力幅；n为循环应变硬化指数，n取0.1～0.2.

2.2 疲劳损伤累积

Miner线性疲劳累积损伤理论具有很好的可验证性和可行性，在工程上得到了广泛应用。设加载历史由δ1，δ2，…，δl共l个不同的应力水平构成，各应力水平下的疲劳寿命依次为N1,N2，…，Nl，各应力水平下的循环次数依次为n1，n2，…，nl，则零件的疲劳寿命[16-17]为

(10)

3 枪管寿命预测及试验验证

以某5.8 mm小口径步枪枪管为研究对象，忽略膛线，将枪管简化为厚壁圆筒，镀层材料为铬，镀层厚度0.01 mm，进行枪管寿命预测计算。为全面评价枪管寿命情况，综合反映射击时枪管的温度场和应力场分布状况，沿枪管轴线选取3个典型截面进行寿命预测，分别为最大膛压截面(A截面)、距膛口150 mm截面(B截面)和距膛口85 mm截面(C截面)，3个截面在枪管轴向的位置示意图如图2所示。

图2 3个截面轴向位置Fig.2 Axial positions of three chosen sections

3.1 枪管温度场求解

由(7)式可知，界面剪切应力与枪管内壁附近温度分布息息相关，因此需要对该枪管在射击过程中的温度场分布进行数值模拟。根据国家军用标准GJB3484—98的要求，该小口径步枪枪管寿命试验一个完整冷却周期的射弹量为150发，共5个弹匣，此150发弹在射击过程中需要按照一定比例分为单发、短点射和连发射击，具体为：单发×15，5发×3，5发×6，5发×6，5发×6，30发×1，其中每射击30发弹需换一次弹匣。

利用有限差分法分别对A、B和C3个截面在一个完整冷却周期内的枪管温度场进行求解。假设射击过程中每一发弹的内弹道参数各自独立且完全相同，3个截面单发加载的火药燃气温度及内壁强迫对流换热系数边界条件如图3所示。

图3 一维径向传热分析内壁边界条件Fig.3 Boundary conditions of inner surface of barrel in 1D radial heat transfer analysis

图4所示为3个截面首发射击时内壁温度变化情况。由图4可见，枪管内壁温度从高到低依次为A截面、C截面和B截面，射击过程中枪管内壁温度在轴向上的分布为两端高、中间低。A截面靠近膛底，对应的膛压最大和火药燃气温度最高，故内壁温度最高；C截面离膛口较近，虽然对应的膛压和火药燃气温度都较低，但由于该处枪管壁厚较薄，且内壁强迫对流换热系数较大，内壁温度和A截面反而相差不大。

图4 首发射击过程中枪管内壁温度变化情况Fig.4 Temperature variation of inner surface of barrel during the first firing

3.2 界面剪切应力计算

将温度场求解获得的3个截面在一个完整冷却周期内的镀层半厚处及两倍镀层厚度处的温度变化与膛压载荷共同代入(7)式，便可计算获得3个典型截面一个完整冷却周期内的界面剪切应力变化情况。

各截面单发加载的膛压载荷如图5所示。对比图4和图5可发现，由于热传递需要时间，镀层半厚处膛压载荷和温度载荷达到峰值的时机并不一致，膛压载荷要先于温度载荷达到峰值。而由膛压载荷引起的周向应力为拉应力，热载荷引起的周向应力为压应力，故在首发弹的射击过程中，镀层内周向正应力会表现为先拉后压。图6所示为首发射击时各截面镀层内周向应力变化情况。由图6可见，膛压越大的位置，其拉应力峰值越大。A截面对应的拉应力和压应力峰值分别为646 MPa和410 MPa，此处膛压载荷应力在首发射击过程占据主导地位。随着射击发数增加，枪管温度升高后，热应力会逐渐占据主导地位，此时膛压载荷的主要作用开始表现为抑制热载荷应力。

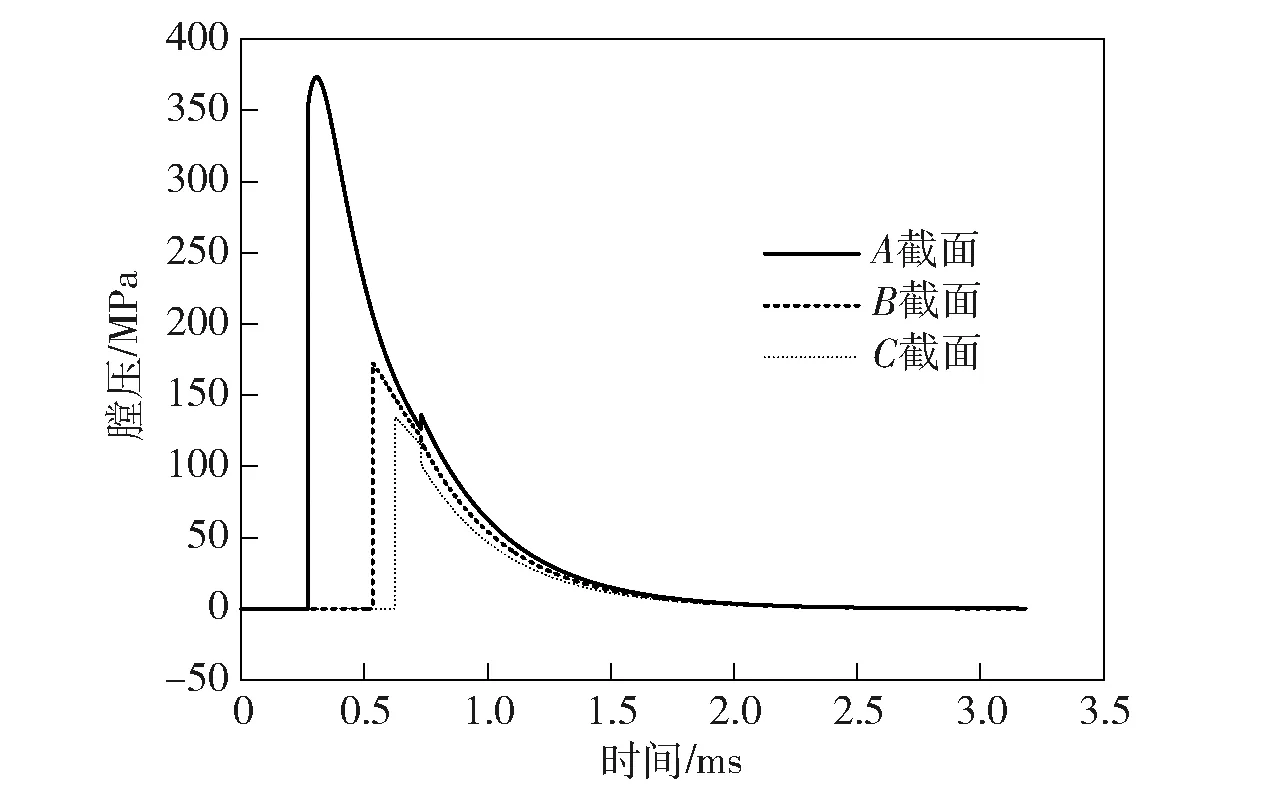
图5 单发膛压载荷Fig.5 Bore pressure load

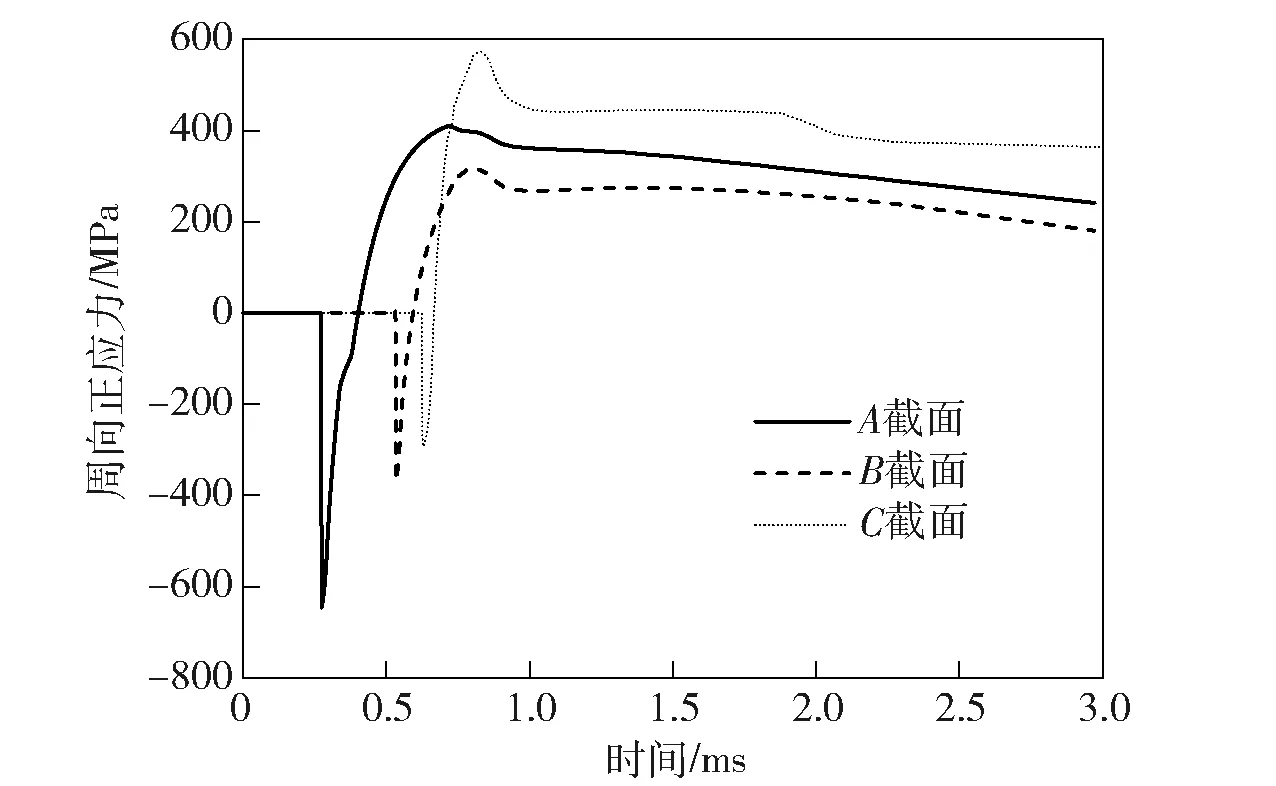
图6 首发射击时镀层内平均周向正应力随时间变化情况Fig.6 Variation of average circumferential stress in coating during the first firing

由(7)式可知，对于开裂后的镀层片段而言，其界面切应力是周向应力Sc和断裂后的镀层长厚比L/h的比值，而断裂后的镀层长厚比等于镀层材料抗拉屈服强度和其剪切强度之比[12]，对于特定镀层而言，L/h有固定的取值范围，在身管的实际射击中发现，开裂后电解沉积铬镀层片段长厚比约为1.5左右[12,18-19]，故本文取1.5作为枪管铬镀层断裂后的典型长厚比，计算150发射击过程中的镀层界面剪切应力。

图7所示为一个完整冷却射击周期内3个截面界面切应力的平均应力变化情况。由图7可见，射击过程中，平均应力的整体变化趋势是随着射弹量增加而变大，但在换弹匣间隙的短暂空冷期内会因枪管温度下降而出现小幅下降。在冷却周期前期，A截面和B截面的平均应力都有一段负值，表明此时镀层内的周向正应力以膛压载荷引起的拉应力为主导。

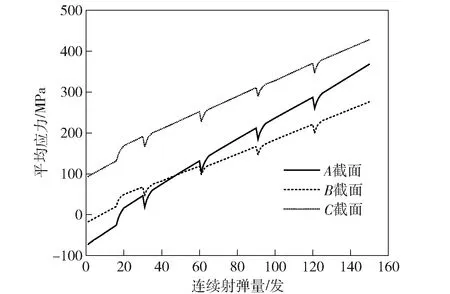
图7 平均应力随射弹量变化情况Fig.7 Variation of mean stress during whole firing process

图8所示为一个完整冷却射击周期内3个截面界面切应力的应力幅变化情况。由图8可见，随着射弹量增加，枪管温度逐渐升高，枪管材料的导热性能也随之下降，进而导致单次射击带来的枪管近壁温度脉冲幅值有所下降，因此应力幅的整体变化趋势随着射弹量增加而降低。对比第1发和最后一发的应力幅大小可发现，在整个射击过程中，3个截面的应力幅下降幅度其实都不大，累积下降量都仅为20 MPa左右。

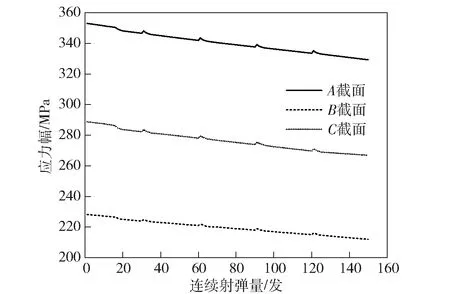
图8 界面切应力幅随射弹量变化情况Fig.8 Variation of interface shear stress amplitude during whole firing process

单次射击过程中，A截面和C截面内壁温度幅值几乎相等(见图4)，则忽略膛压作用时，其对应的热应力幅值应该相差不大。但是由于A截面处的膛压应力远大于C截面，从而导致热压耦合作用下两截面对应的切应力峰值谷值都不尽相同(见图6)。因此A截面的应力幅在整个冷却周期内始终比C截面大20%左右。

3.3 枪管材料抗拉强度

本文研究的枪管材料为高强度合金钢，抗拉强度采用随温度变化的数据，表1所示为试验实测的该枪钢不同温度下对应的抗拉强度数据。

表1 不同温度下的枪管材料抗拉强度Tab.1 Tensile strength of gun barrel material at different temperatures

对表1所示数据进行数据拟合，获得该枪钢材料在20～700 ℃范围内抗拉强度随温度连续变化的曲线，如图9所示。拟合后的抗拉强度随温度变化公式可表示为

σb=1 254.9-49.96eT/227.99，

(11)

式中：T为材料温度。

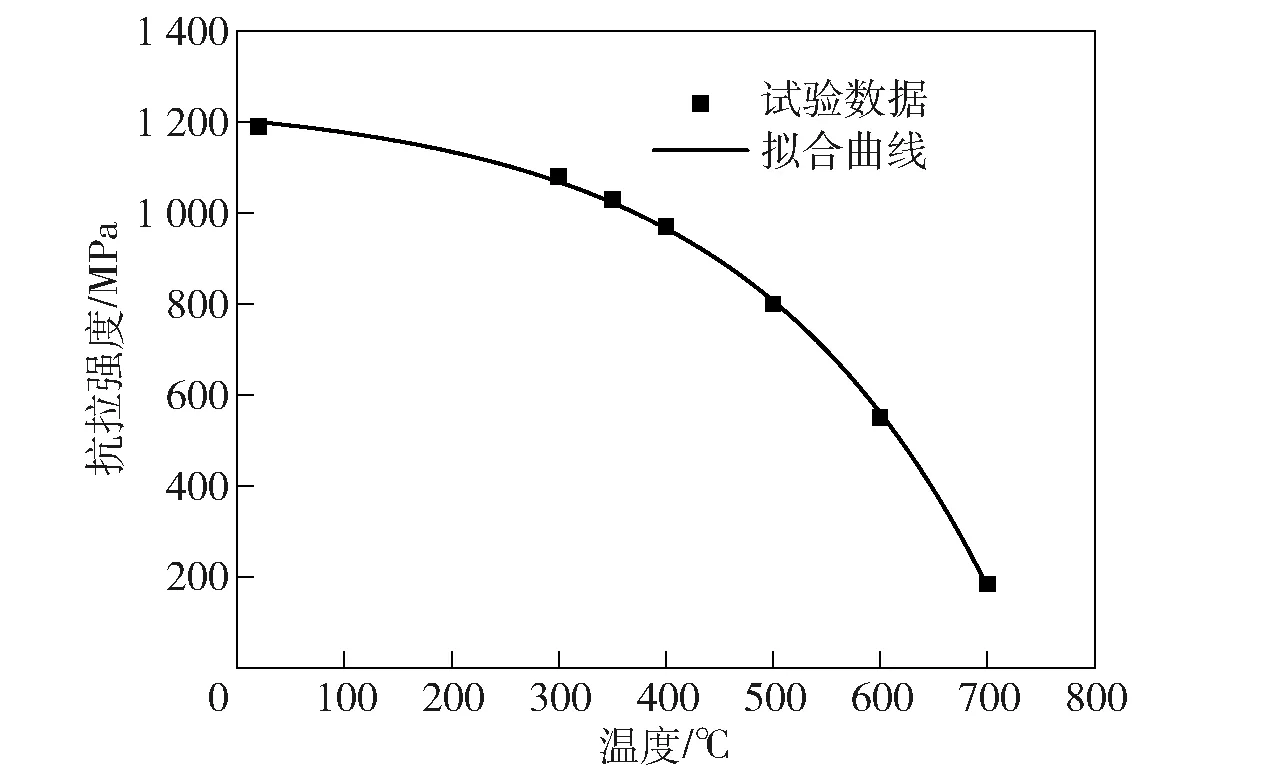
图9 枪管材料抗拉强度随温度变化拟合曲线Fig.9 Fitted curves of variation of tensile strength at different temperatures

图9所示为枪管材料抗拉强度随温度变化拟合曲线。由图9可见，该枪管材料在温度低于400 ℃时，抗拉强度随温度升高而下降的趋势较慢，但在温度超过400 ℃后，随着温度上升，抗拉强度开始大幅下降，且温度越高、下降率越高。实际射击时，枪管近壁层温度都高达数百摄氏度，且会随着射弹量增加而增高，在这种情况下再采用常温抗拉强度进行寿命预测，显然是不符合实际情况的。

出于极端工况考虑，取各单发射击时的界面抗拉强度最小值——界面温度达到峰值时的界面抗拉强度进行枪管寿命预测。图10所示为一个完整冷却周期内，枪管钢铬交界面温度峰值随射弹量增加变化情况。由图10可见，A、C截面的界面温度峰值在整个射击过程中都大于400 ℃，而B截面的界面温度在整个射击过程中都要比A、C截面低100 ℃以上。

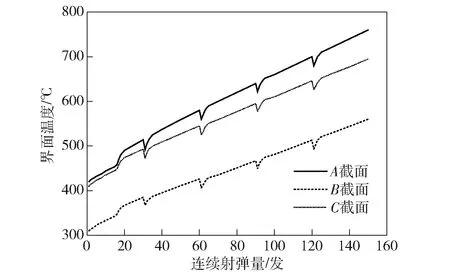
图10 枪管界面温度峰值随射弹量变化情况Fig.10 Variation of peak interface temperature during whole firing process

结合(11)式及图10界面温度变化，计算得到各截面对应的枪管钢铬结合面抗拉强度随射弹量增加变化情况如图11所示。由图11可见，在射击开始阶段，由于枪管温度较低，3个截面对应的界面抗拉强度之间差异并不是很大，而随着射弹量增加，枪管温度升高后，各截面对应的界面抗拉强度之差逐渐增大。然而由于材料高温强度缺乏700 ℃以上的实测数据，而根据拟合公式计算出700 ℃以上高温强度都极低甚至出现负值。事实上，当温度超过700 ℃时，钢材料晶格会发生体心立方(BCC)到面心立方(FCC)的相变，材料强度下降幅度也会变缓。而在本文研究的3个截面中，只有A截面的界面温度在射击过程中超过了700 ℃，且界面温度超过700 ℃的时期仅占整个冷却周期非常小的一部分，在此时期内是否采用更低的抗拉强度进行寿命预测，对A截面的整体疲劳累积寿命预测结果并不会产生颠覆性影响。故本文在计算A截面寿命时，温度超过700 ℃后的界面抗拉强度都采用700 ℃时的数据。

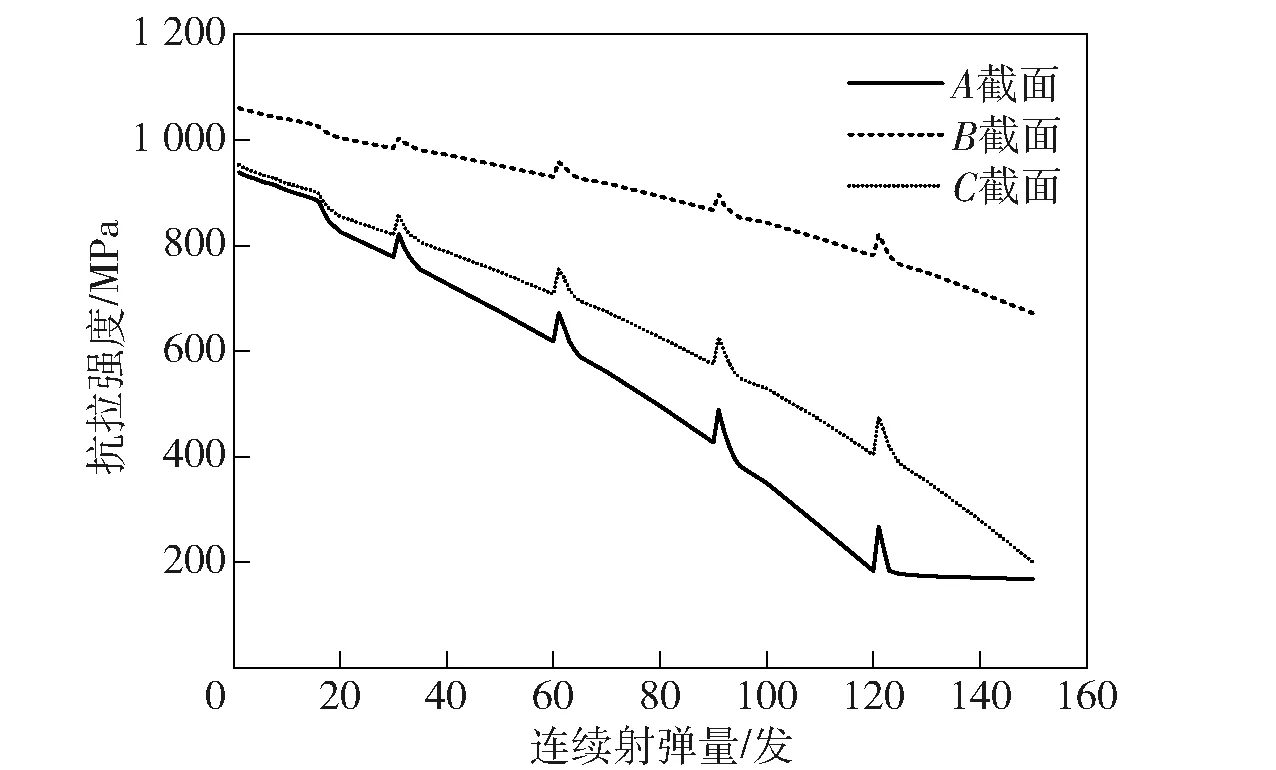
图11 枪管界面抗拉强度随射弹量变化情况Fig.11 Variation of interface tensile strength during whole firing process

3.4 寿命预测结果及试验验证

由图10可知，B截面在射击过程中温度较低，对应的应力幅最低(见图8)，而界面抗拉强度最大(见图11)。最终进行寿命预测得出的B截面等幅载荷寿命和疲劳累积损伤寿命都远大于A、C截面。显然，根据短板理论，枪管的寿命预测结果不能采用B截面寿命，而A、C两截面的预测寿命更为接近枪管真实寿命，故下文仅以应力状态较为接近且寿命预测结果相差不大的A、C截面为比较对象进行分析。

图12所示为A、C截面对应的等幅载荷寿命随射弹量增加变化情况。如图12所示，整个射击过程中C截面的等幅载荷寿命都大于A截面。虽然射击过程中，C截面对应的镀层内周向正应力峰值大于A截面(见图6),界面切应力平均应力也始终大于A截面(见图7)，但其应力幅却小于后者(见图8)，且界面抗拉强度较大(见图11)。由此可见，镀层的剪切疲劳寿命主要受切应力应力幅和界面抗拉强度大小影响，而并非受界面切应力的峰值或平均应力大小控制。切应力应力幅越大，界面抗拉强度越小，则镀层的剪切疲劳寿命越小。随着累积射弹量增加，两截面的切应力应力幅整体上呈略微下降趋势，但其等幅载荷寿命却随着界面抗拉强度的下降而迅速衰减，表明连续射击过程中近壁温度升高带来的界面抗拉强度下降，是导致镀层破坏及枪管寿终的主要诱因之一。

表2所示为不同累积射弹量时镀层等幅载荷寿命及相对于第1发的下降率。由表2可见：当射击进行到第2个弹匣累积射弹量达到60发时，A、C截面的等幅载荷寿命都已不足第1发的一半；当射击进行到第5个弹匣时，A、C截面的等幅载荷寿命衰减率分别达到95.5%和87.9%，材料高温强度对枪管寿命的影响可见一斑，提高枪管材料高温强度对枪管寿命的提升意义重大。

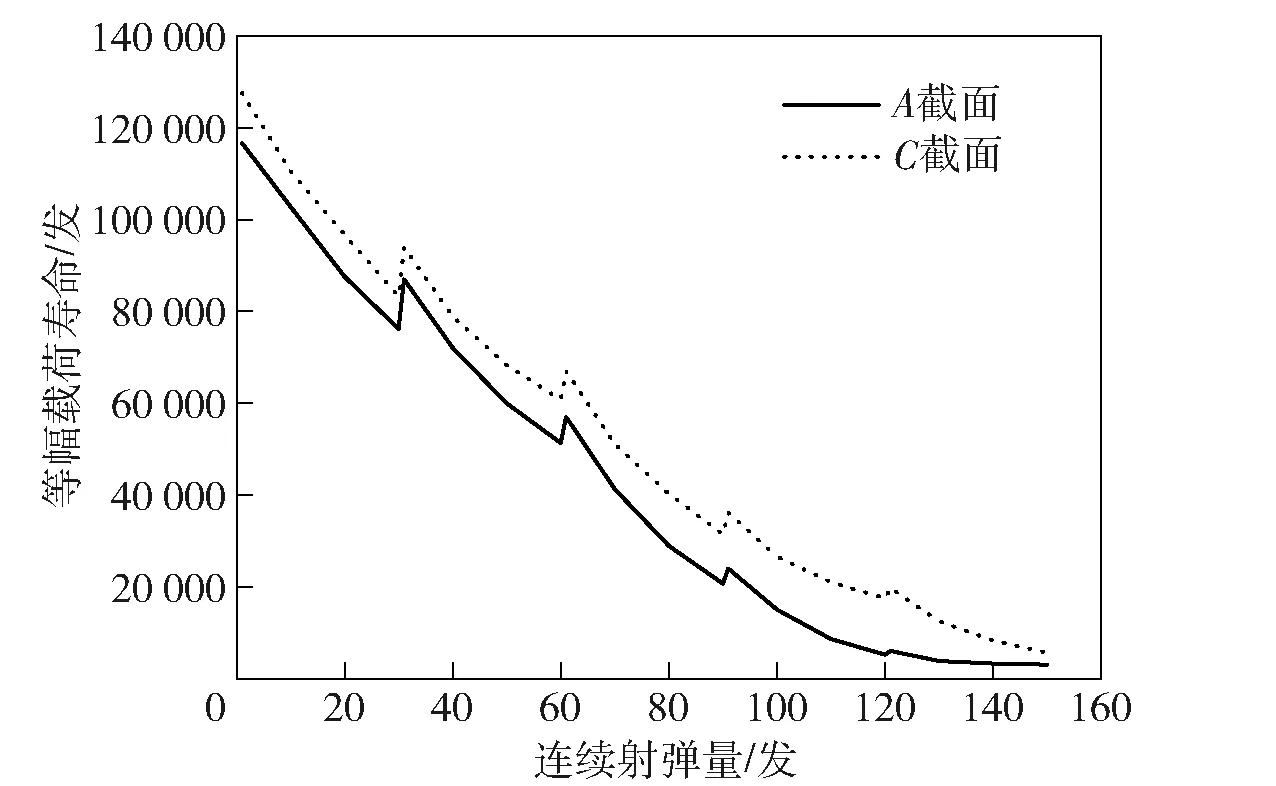
图12 枪管等幅载荷寿命随射弹量变化情况Fig.12 Variation of barrel life under constant amplitude loading during whole firing process

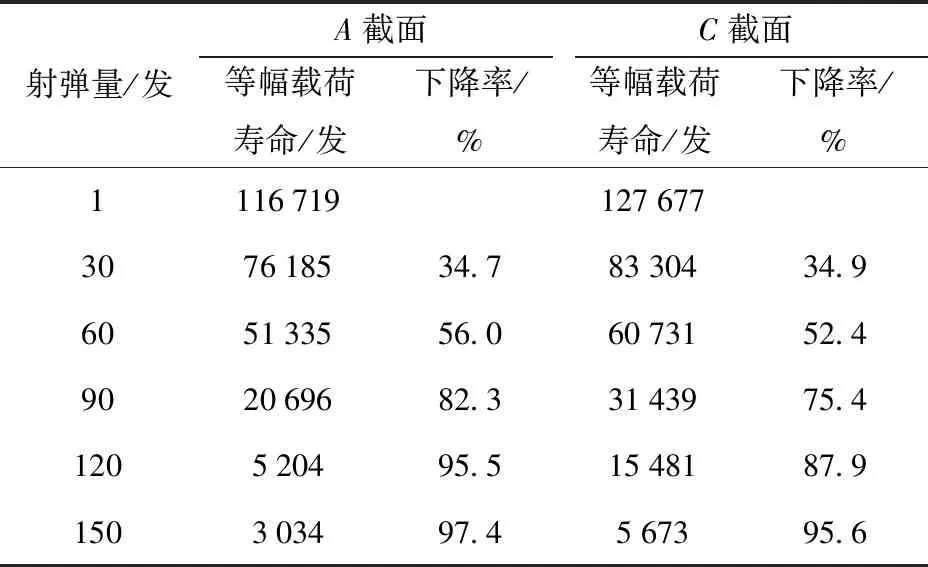
表2 不同射弹量时的枪管等幅载荷寿命及寿命下降率Tab.2 Barrel lives under constant amplitude loading and life droop rates for different firing shots

换弹匣间隙的短暂空冷带来的枪管近壁温度下降引起了枪管应力状态的一系列变化，如平均应力下降及界面抗拉强度回升等，这一系列变化最终导致枪管的等幅载荷寿命在换弹匣后再次射击时会出现短暂回升。以A截面为例，第30发弹对应的等幅载荷寿命为76 185发，第31发对应的等幅载荷寿命为87 051发，比第30发上升了14.3%，与第20发对应的87 608发非常接近。几秒钟的短暂空冷即可以带来枪管等幅载荷寿命的大幅提升，因此实际射击中，采用科学合理的射击规范，如尽量采用单发或者短点射以减缓枪管近壁温度的上升速度，并及时冷却过热的枪管，可以有效提高枪管寿命。

根据疲劳损伤累积理论，计算得出A、C截面对应疲劳损伤累积寿命分别为10 446发和15 569发，A截面的疲劳寿命在本文研究的3个截面中最低。由于A截面的膛压在枪管中最高，在射击过程中承受热冲击作用的时间最长，工作环境最为恶劣，故可将A截面所处区域，即最大膛压区的寿命(10 446发)视为整根枪管的疲劳寿命。为了验证上述寿命预测模型及预测结果的正确性，对该小口径步枪进行枪管寿命试验验证。试验验证枪两支，分别编号为1号枪和2号枪，寿命试验流程按照国家军用标准GJB3484—98枪械性能试验方法执行。对于枪管烧蚀寿命的寿终判别标准，目前有初速下降率、横弹孔率和散布密集度R50大小3个标准，其中R50为包含总测弹量一半弹着点的最小圆半径，但在对本文所研究的小口径步枪历次寿命试验中发现，该枪枪管全部是因为R50值超标而寿终，因此在实际应用中均以R50超标时的射弹数作为该小口径步枪枪管的寿命。寿命试验中，每隔一定阶段测试被试枪支在100 m距离上固定夹持射击的立靶密集度R50值，寿终判据为R50>11 cm.表3所示为两支被试枪支不同试验阶段对应的R50变化情况以及寿终时的累计射弹量。