中日“直线与圆的位置关系”教材内容比较研究
2020-01-06叶立军傅勉
叶立军 傅勉

【摘 要】 选取“直线与圆的位置关系”内容,从宏观与微观这两个角度对中日三版教材进行比较分析,得到人教版教材生活背景所占比例高于另外两版教材、浙教版教材注重不同学科间的交叉综合等结论.由此得到启示:教材应丰富知识背景,发展数学建模素养;适当设置提示,培养学生自主学习能力.教学过程中应关注过程教学,培养学生高阶思维能力;适当拓展知识,创设综合性问题落实深度学习.
【关键词】 圆与直线的位置关系;教材研究;人教版;浙教版;东京版
1 问题的提出
教材既是教师的“教本”,也是学生的“学本”,是学校教育和课堂教学的基本要素和基本依据,新时代建设新教材,不仅需不忘本来,大力弘扬中华优秀传统文化,更应吸收外来,面向未来,不断提升教材质量[1].
几何学作为数学中最基本的研究内容之一,向来是被关注的重点.而教师作为课改的主力军与参与者,能否准确把握教材、理解几何知识要点、分析几何知识现状至关重要[2].“圆与直线的位置关系”是数与形的有机结合,圆的切线的性质及其相关定理在几何学习与现实生活中广泛应用,因此,开展教材比较显得很有必要.
2 研究对象
选取初中人教版《义务教育课程标准实验教科书·数学》、浙教版《义务教育教科书·数学》以及东京书籍株式会社2012年出版发行的《新数学》(以下简称人教版、浙教版与东京版)的“直线与圆的位置关系”部分内容作为研究对象.
3 教材的宏观比较
3.1 编排顺序比较研究
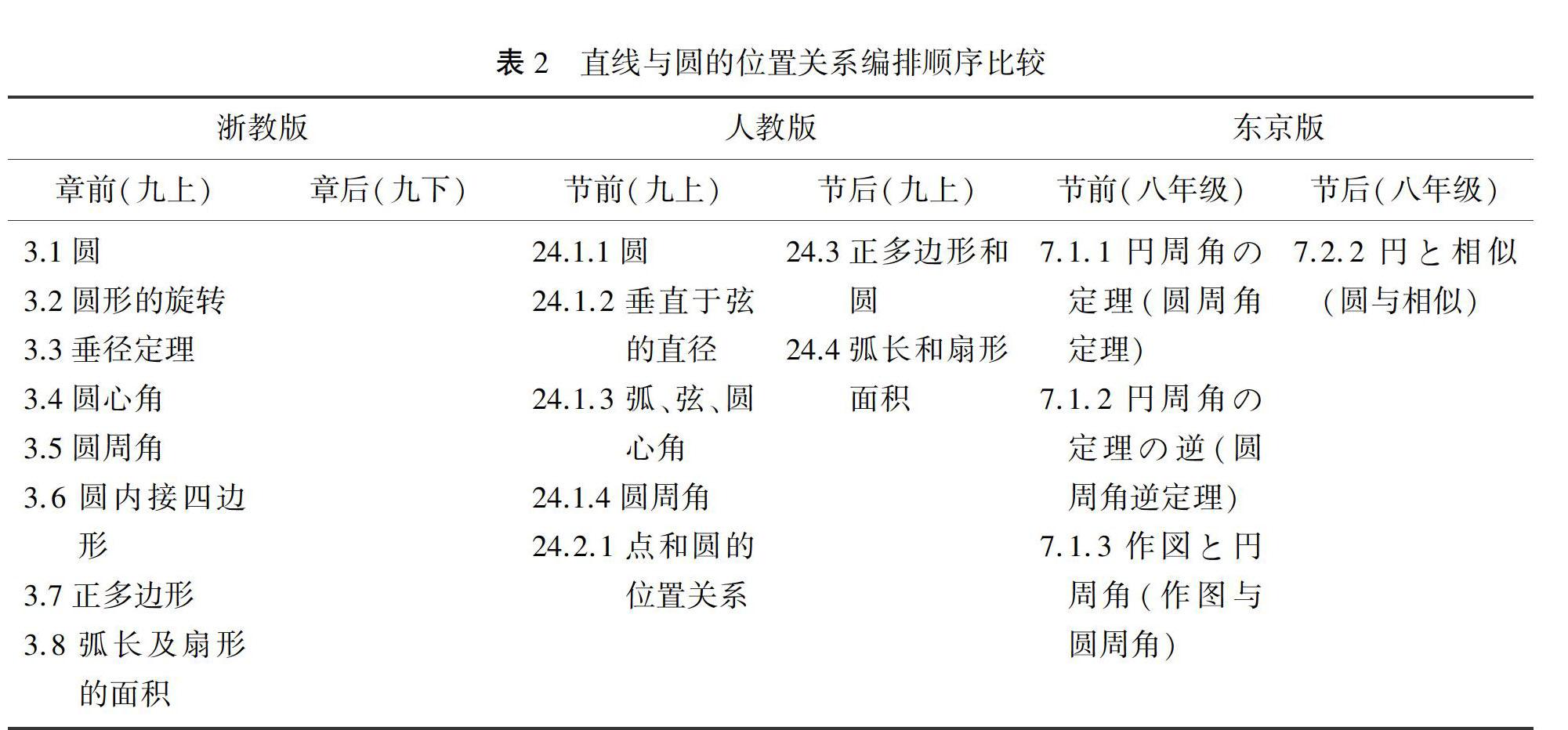
将三版教材中直线与圆的位置关系内容按编排顺序进行比较,如表2所示.
由表2可知,三版教材都按照“圆周角定理→直线与圆的位置关系”顺序编写.浙教版与人教版在圆的定义之后,编排了弧、弦、垂径定理等内容.此外,人教版善用类比思想,通过点与圆的位置关系推理得到直线与圆的位置关系.3.2 体例结构比较研究
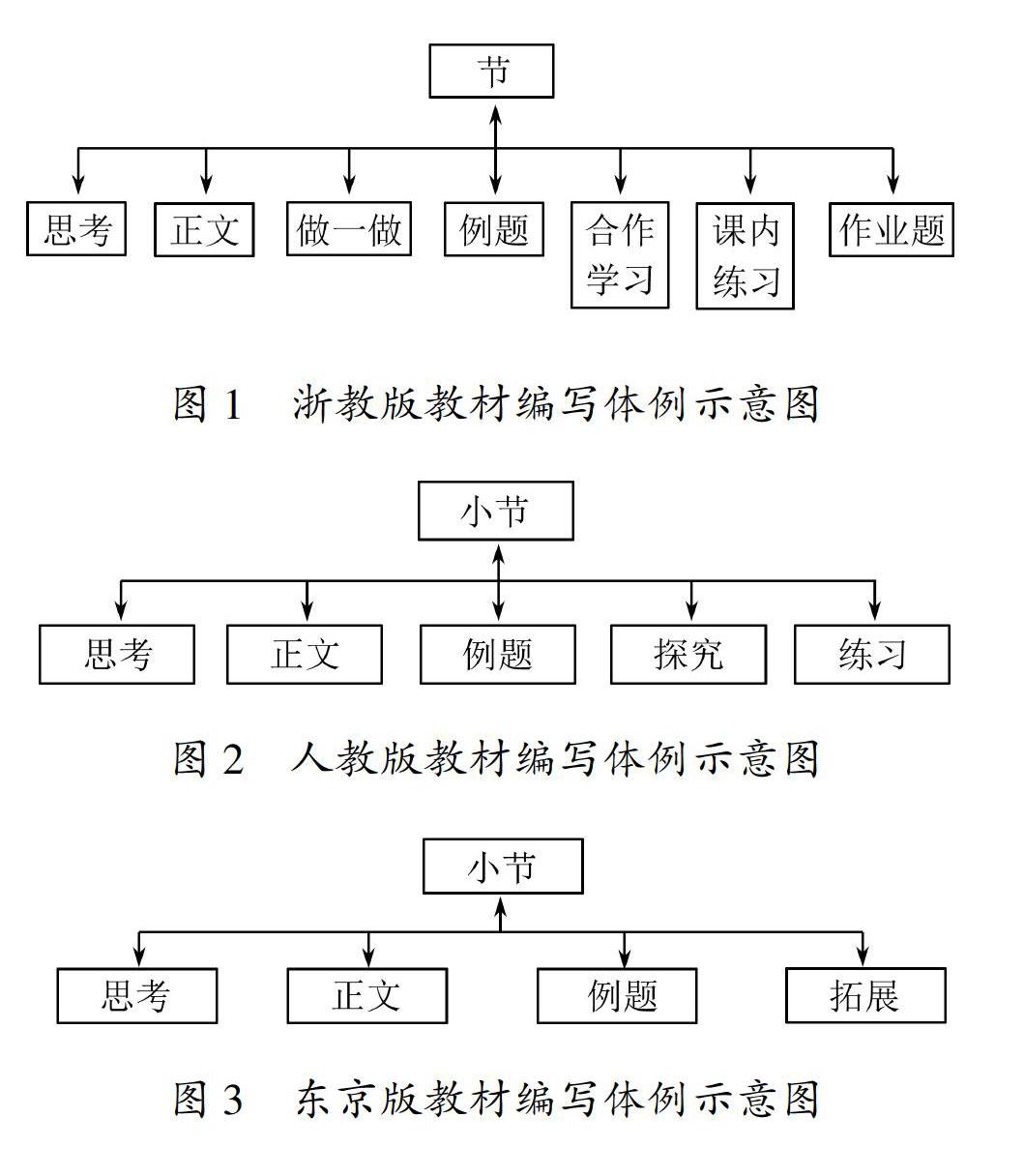
对三版教材中关于直线与圆的位置关系内容的编写体例进行比较,如图1、2、3所示.
由图1、2、3可知,三版教材中该内容主要是以“思考→正文→习题”的模式进行教学,在具体的体例结构上则存在差异.第一,习题设置.浙教版与人教版在每一课时后都设置练习,东京版则在一整节后编入A、B两版习题.此外,东京版的例题没有解答过程,仅添设提示;第二,探究模塊.浙教版在合作学习中归纳得到圆的切线的性质,人教版中的探究证明了切线长定理,东京版不含探究模块.4 教材的微观比较
4.1 知识呈现方式的比较
我们对知识点呈现方式进行分类,如表3所示.
对切线判定定理以及切线长定理进行比较,结果如表4、表5所示.
由表4可知,在知识体验与讲解方面,浙教版与东京版设计相似的作图环节,引导学生体会切线与半径之间的联系,而人教版通过看图思考发现联系.在知识表征方面,人教版与浙教版的表征一致,东京版则借助切线的作图方法说明切线判定定理.在知识拓展方面,东京版的思考题结合圆周角定理,引出切线长定理,另外两版教材并无拓展内容.
由表5可知,在知识导入方面,浙教版借助传统文化“抖空竹”导入新知,东京版则采用动手作图的方式.在知识体验与讲解方面,人教版与东京版通过探究活动先进行证明,后给出定理,而浙教版与之相反.在知识应用与拓展方面,浙教版与东京版选取几何例题以巩固基础,人教版则将其应用于生活.最后,三版教材的延伸内容均涉及多边形的内切圆.
4.2 知识背景的比较
将知识背景分为生活、文化、科学与数学四类后,我们对三版教材中直线与圆的位置关系内容的知识点与例习题按照知识背景进行统计,具体如图4所示.
由图4可知,三版教材都涉及数学与生活背景,不同的是,人教版与浙教版还涉及文化与科学背景.参照具体数值,三版教材中数学背景占比最大,其次为生活背景,且人教版生活背景所占比例最高.
4.3 例习题综合难度的比较图5 三版教材例习题综合难度比较图
为比较直线与圆的位置关系内容的例习题综合难度,此处引入鲍建生数学课程综合难度模型[3].根据统计所得数据,计算每个难度因素的加权平均,并绘制相应图5.其中,浙教版的例习题总量为62题,人教版为22题,东京版为9题.
从整体看,三版教材的例习题背景数值最低,可见,这三版教材都较少关注知识背景.从单个因素来看,三版教材都以数学背景为主,不同的是,浙教版的例习题还涉及科学背景,注重不同学科间的交叉综合.在运算方面,东京版的数值略高于另外两版教材,说明其重视学生的运算能力.在知识含量上,三版教材的例习题都以单个或两个知识点为主.
4 研究启示
4.1 丰富知识背景,发展数学建模素养
数学建模过程体现了生活语言与数学语言的互译,充分展现了学生用数学眼光看世界的综合素养[6].因此教材可以适当增加生活化、多元化的知识背景,在例、习题中创设基于实际且能够促进知识深化的问题情境,向学生渗透数学与世界的联系,从而在运用数学语言描述实际现象、分析实际问题,借助数学知识建构数学模型、解决实际问题的过程中发展其数学建模素养.
4.2 适当设置提示,培养学生自主学习能力
教材作为学习之本,具备一定的引导作用,能够调动学生的主观能动性,使其自主学习、探究、巩固与延伸知识.为增强引导作用,教材应设置紧扣内容且开拓思维的有效提示,这不仅能帮助教师在课堂中突破重点、难点,更有益于学生在课堂外有效预习、复习,培养其自主学习能力.例如在教材例题的编写上,可以适当简略答案,以启发式提问或关键点提示的方式帮助学生突破思维难点、落实问题本质、引发深度思考,从而内化知识、强化能力.
4.3 关注过程教学,培养学生高阶思维能力
忽视学生的概念形成过程、知识应用过程等,往往会导致知识的理解流于表面,学生思维也停留在“识记、理解和简单应用”的低阶状态.因此,教师应关注过程教学,通过对教学内容及学生的学习过程与方式的精心设计,使学生能够简约地、模拟地“经历”发现知识的关键环节[7],充分地、切实地感受应用知识的实践过程。在实践与思维的交互中,引导学生建立思维支点、把握问题求解、学会批判反思,从而逐步提炼数学思想,培养综合应用的高阶思维能力.
4.4 适当拓展知识,创设综合性问题落实深度学习
实践证明,适当拓展知识不仅可以完善认知结构、拓宽解题思路,更能促进知识的迁移.而知识的拓展不仅仅是本学科知识纵向的内容扩充与结构完善,更是不同学科知识横向的兼容并蓄与相互理解.因此教师在教学过程中,可以适时安排拓展环节,根据教学内容、教学目标、学情等合理组织跨单元、跨学科知识,借助真实情境创设综合性问题,引导学生在分析、猜想、应用与反思的过程中经历解决问题的过程、掌握解决问题的要领,从而进一步建构思维框架,有效落实深度学习.
参考文献
[1]黄强.新时代教材建设:理念与实践[M].人民教育出版社,2018.9:5-10
[2]王运君.新课标下中学教师几何教学的现状分析与对策[D].海南师范大学,2014
[3]鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望,2002,31(09):48-52
[4]叶立军,傅建奇.中美初中几何教材比较研究——以“全等三角形”为例[J].中学数学杂志,2017(10):35-41
[5]叶立军,戚方柔.中美初中“圆”内容比较研究——以浙教版、人教版、美国GMH教材为例[J].中学数学月刊,2020(04):44-48
[6]陈柳娟,林晴岚.基于数学核心素养的教师教育教学思考[J].教学与管理,2017(03):109-111
[7]郭华.深度学习及其意义[J].课程·教材·教法,2016,36(11):25-32
