概率统计、简易逻辑、计数原理、二项式定理、算法语言和复数核心考点B 卷参考答案

2020-01-06

中学生数理化(高中版.高考数学) 2019年12期

关键词：裁判科目命题

一、选择题

1.A 2.D 3.D 4.A 5.B 6.B

7.C 8.C 9.D 10.A 11.B 12.B

二、填空题

20.-5 21.72 22.300

三、解答题

命题q：函数f(x)=2x3-mx-1 在[-1，1]上单调递减。若q 真，则f'(x)=6x2-m≤0 在x∈[-1，1]上恒成立，只需m≥6x2，解得(6x2)max=6，x∈[-1，1]。

若命题p∧q 与命题¬p 都为假命题，可知p 真，q 假。

所以实数m 的取值范围为(3，6)。

24.(1)设甲、乙、丙三个家庭能住在同一单元为事件A，则P(A)=

(2)设甲、乙、丙三个家庭中恰有两个家庭能住在同一单元为事件B，则P(B)=1-

所以甲、乙、丙三个家庭中恰有两个家庭能住在同一单元的概率为

25.(1)设一位顾客进店购物结算时间为T，根据统计图表可知，T 的可能取值为10，20，40，60，所以P(T=10)=0.4，P(T=20)=0.2，P(T=40)=0.3，P(T=60)=0.1，所以该顾客进店购物结算时所用时间的期望为10×0.4+20×0.2+40×0.3+60×0.1=26(秒)。

(2)依题意可知，每个顾客各自的付款时间是相互独立的，若三位顾客付款时间总计不少于2 分钟，则三位顾客的付款时间可能有如下情况：

①三位顾客都是60秒；

②二位顾客是60 秒和另外一位顾客可以是10秒，20秒，40秒中任意一个；

③一位顾客60秒，另外两位顾客可以是20秒，40秒或40秒，40秒；

④三位顾客都是40秒。

所以对应的概率为P=0.13+C23×0.12×(0.4+0.2+0.3)+C13×0.1×(C12×0.2×0.3+0.3×0.3)+0.33=0.118。

所以该顾客等候时间不少于2分钟的概率为0.118。

26.(1)第1局是由甲担任裁判，得到第4局仍是甲担任裁判的情况是第2局甲胜，第3局甲负，设A1表示第2局的结果为甲胜，A2表示第3局的结果为甲负，A 表示第4 局为甲当裁判，所以第4 局仍是甲担任裁判的概率为P(A)=P(A1A2)=P(A1)P(A2)=

(2)因为丙当了2局裁判，所以甲乙比赛2局，甲丙比赛6-2=4(局)；甲乙比赛2局，乙丙比赛5-2=3(局)。

以丙的比赛过程来看整个比赛，甲丙+乙丙+丙裁判=4+3+2=9(局)。

所以甲、乙、丙3人进行的擂台赛共进行了9局，其中甲担任裁判的局数为3局，从小组赛中，甲、乙、丙比赛的所有场次中任取2局，基本事件总数均是由甲担任裁判包含的基本事件个数

从小组赛中，甲、乙、丙比赛的所有场次中任取2 局，则均是由甲担任裁判的概率是

27.(1)由频率分布直方图知得分在［70 ，80）上的频率P=1-(0.01-0.015-0.02-0.015-0.01)×10=0.3。

(2)由(1)可知各组的中间值及对应的频率如表1：

表1

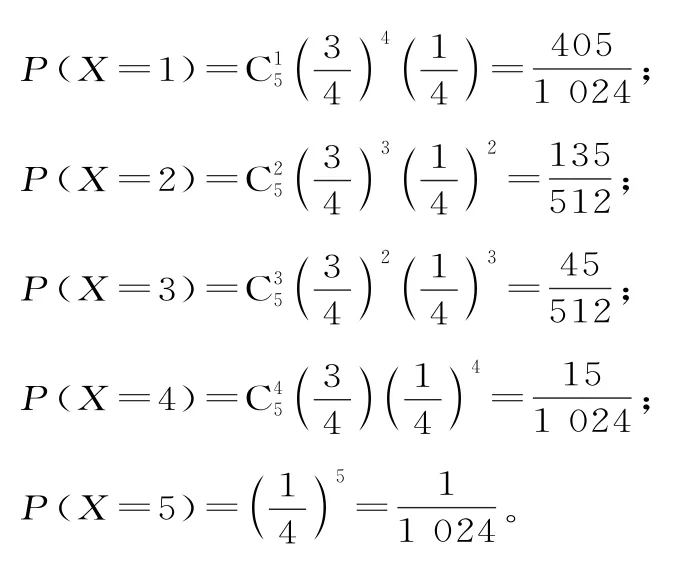
所以X 的分布列为表2：

表2

28.(1)由频数分布表可知，日纯利润在区间[5，7)内的频率为

所以μ=6.85。

又σ=1.44，所以P(3.97＜Z＜8.29)=P(6.85-2.88＜Z＜6.85+1.44)=P(μ-2σ＜Z ＜μ+σ)=P(μ-σ＜Z ＜μ+σ)+μ+σ)]=0.818 5。

故该大型超市1 000天内日纯利润在区间(3.97，8.29)内的天数为1 000×0.818 5≈819。

对应奖励方案一：设小张每日奖金金额为Y，则可能取值为70，90，其对应的概率均为

对于奖励方案二：设小张每日奖金金额为Q，则Q 的所有可能取值为50，100，150，200。

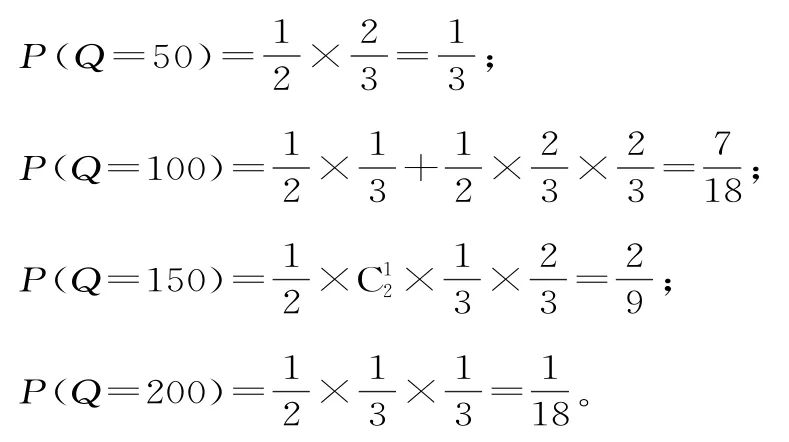
所以Q 的分布列为表3：

表3

所以E(Q)＞E(Y)。

从数学期望的角度看，小张选择奖励方案二更有利。

解得t=48。

由题意知ξ 的可能取值为1，2，3。

所以ξ 的分布列为表4：

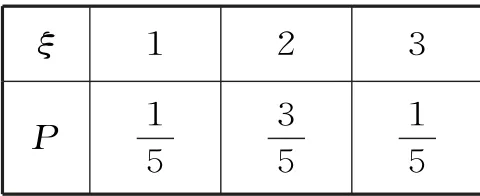
表4

30.(1)经统计可知，样本40人中，选修化学、生物的人数分别为24，11，则可估计高一年级选修相应科目的人数分别为720，330。根据每个选修班最多编排50人，且尽量满额编班，得对应开设选修班的数目分别为15，7。现有化学、生物科目教师每科各8人，根据每位教师执教2个选修班，当且仅当1门科目的选课班级总数为奇数时，允许这门科目的一位教师执教一个班的条件，知生物科目需要减少4名教师，化学科目不需要调整。

(2)根据表格中的数据进行统计后，制作列联表如表5：