2019 年高考概率统计考点聚焦

■江苏省高邮市第一中学 耿广祥

2019 年高考对概率统计的考查主要围绕“频率分布直方图、独立性检验、古典概型、随机变量的分布列和期望的计算、二项分布”等核心考点展开，重在考查同学们应用概率统计知识解决实际问题的能力。

聚焦1——统计图表与独立性检验

例1(2019年全国Ⅰ卷文17)某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到表1所示的列联表：

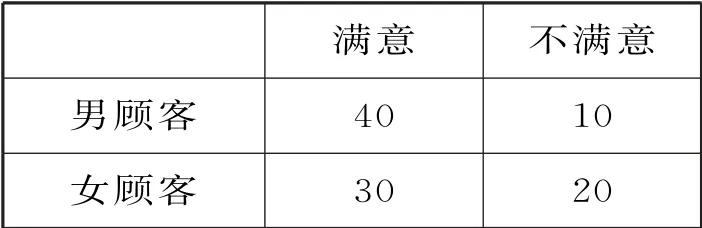
表1

(1)分别估计男、女顾客对该商场服务满意的概率；

(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?

附：K2=

表2

解析：(1)由题中表格可知，50名男顾客对商场服务满意的有40人，所以男顾客对商场服务满意的概率为50 名 女顾客对商场满意的有30人，所以女顾客对商场服务满意的概率为

(2)由题中的列联表可知 K2=因为4.762＞3.841，所以有95%的把握认为男、女顾客对该商场服务的评价有差异。

点评：将统计表格给出的数据代入卡方公式，计算出的数据与临界值比较可得相关性判断的程度结论，这一直是高考命制统计试题的处所，应引起考生的高度重视。

聚焦2——事件关系及应用

例2(2019 年全国Ⅰ卷理15)甲、乙两队进行篮球决赛，采取七场四胜制(当一队赢得四场胜利时，该队获胜，决赛结束)。根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”。设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4∶1获胜的概率是____。

解析：甲队以4∶1 获胜，即前五场甲队获胜为互斥的两类事件，先分类后应用独立事件分步算概率，前四场中有一场客场输，第五场赢时，甲队以4∶1获胜的概率是0.63×0.5×0.5×2=0.108；前四场中有一场主场输，第五场赢时，甲队以4∶1获胜的概率是0.4×0.62×0.52×2=0.072。

综上所述，甲队以4∶1获胜的概率P=0.108+0.072=0.18。

点评：互斥事件A，B 满足概率加法公式P(A+B)=P(A)+P(B)，而独立事件A，B 满足概率乘法公式P(AB)=P(A)P(B)。一个复杂的随机事件，往往可以拆分成若干个互斥事件的和，而每个互斥事件又可以拆分为若干个相互独立事件的积。由于本题题干较长，因此，易错点之一就是能否静心读题，正确理解题意；易错点之二是思维的全面性是否具备，要考虑甲队以4∶1获胜的两种情况；易错点之三是能否准确计算。

聚焦3——统计图表与古典概型的网络交汇

例3(2019年北京卷文17)改革开放以来，人们的支付方式发生了巨大转变。近年来，移动支付已成为主要支付方式之一。为了解某校学生上个月A，B 两种移动支付方式的使用情况，从全校所有的1 000 名学生中随机抽取了100人，发现样本中A，B 两种支付方式都不使用的有5 人，样本中仅使用A 和仅使用B 的学生的支付金额分布情况如表3：

表3

(1)估计该校学生中上个月A，B 两种支付方式都使用的人数。

(2)从样本仅使用B 的学生中随机抽取1人，求该学生上个月支付金额大于2 000元的概率。

(3)已知上个月样本学生的支付方式在本月没有变化。现从样本仅使用B 的学生中随机抽查1 人，发现他本月的支付金额大于2 000元。结合(2)的结果，能否认为样本仅使用B 的学生中本月支付金额大于2 000元的人数有变化? 说明理由。

解析：(1)利用频率近似概率可得满足题意的人数，由表3可知仅使用A 的人数有30人，仅使用B 的人数有25人，由题意知A，B两种支付方式都不使用的有5 人，所以样本中两种支付方式都使用的有100-30-25-5=40(人)，所以全校学生中两种支付方式都使用的有

(2)利用古典概型计算公式求概率，因为样本中仅使用B 的学生共有25人，只有1人支付金额大于2 000 元，所以该学生上个月支付金额大于2 000元的概率为

(3)结合概率统计相关定义给出结论，由(2)知支付金额大于2 000元的概率为因为从仅使用B 的学生中随机调查1人，发现他本月的支付金额大于2 000 元，依据小概率事件它在一次试验中是几乎不可能发生的，所以可以认为仅使用B 的学生中本月支付金额大于2 000 元的人数有变化，且比上个月多。

点评：正确找出随机事件A 包含的基本事件的个数n(A)和试验中基本事件的总数n(Ω)，代入公式求解古典概型。其中明确所求事件本身含义，利用枚举法、树状图法和列表法计数，或构建基本事件空间计数，利用对立事件简化计数是求解的关键。借助小概率事件进行决策凸显概率的应用性。

聚焦4——离散型随机变量的概率分布列和期望

例4 (2019年全国Ⅱ卷理18)11分制乒乓球比赛，每赢一球得1 分，当某局打成10∶10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束。甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立。在某局双方10∶10平后，甲先发球，两人又打了X 个球该局比赛结束。

(1)求P(X=2)；

(2)求事件“X=4且甲获胜”的概率。

解析：由随机变量X=2，X=4 的意义构建互斥事件分类和独立事件分步算概率。

(1)由题意可知，P(X=2)所包含的事件为“甲连赢两球或乙连赢两球”，所以P(X=2)=0.5×0.4+0.5×0.6=0.5。

(2)由题意可知，P(X=4)所包含的事件为“前两球甲乙各得1 分，后两球均为甲得分”，所以P(X=4)=0.5×0.6×0.5×0.4+0.5×0.4×0.5×0.4=0.1。

点评：离散型随机变量的取值实质是互斥事件分类的简单表示，相互独立事件同时发生分步算概率，本题能否通过题意得出P(X=2)及P(X=4)所包含的事件(先分类，每类下再分步)是解题的关键，考查考生从题目中获取所需信息和推理计算的能力。

聚焦5——构建二项分布模型

例5(2019 年天津卷理16)设甲、乙两位同学上学期间，每天7：30之前到校的概率均为假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立。

(1)用X 表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量X 的分布列和数学期望；

(2)设M 为事件“上学期间的三天中，甲同学在7：30 之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件M发生的概率。

解析：构建二项分布的模型算期望，借助互斥事件分类，独立事件分步，局部构建二项分布模型算概率。

(1)因为甲同学上学期间的三天中到校情况相互独立，且每天7：30之前到校的概率均为，从而P(X=k)=

所以随机变量X 的分布列为表4：

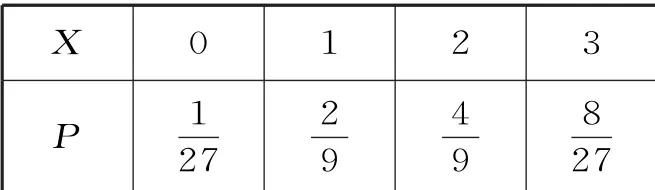
表4

(2)设乙同学上学期间的三天中7：30之前到校的天数为Y，则{X=3，Y=1}∪{X=2，Y=0}。

由题意知事件{X=3，Y=1}与{X=2，Y=0}互斥，且事件{X=3}与{Y=1}，事件{X=2}与{Y=0}均相互独立，从而由(1)知P(M)=P({X=3，Y=1}∪{X=2，Y=0})=P(X=3，Y=1)+P(X=2，Y=0)=P(X=3)·P(Y=1)+P(X=2)·P(Y=0)=

点评：有关随机变量的分布列与数学期望问题，其中互斥事件和相互独立事件的概率计算是基础，有时需合理构建独立重复试验，利用二项分布模型可简化概率计算，有时与导数相结合可求得其最值点。