简易逻辑题型中的易错题归类剖析

■江苏省口岸中学 杨 翠

运用命题间相互关系及命题的否定形式解题是常用逻辑用语这一部分的重点题型，它能涉及不等式、方程、函数等许多方面的知识。而在阐述充分与必要条件这些内容的问题时，最容易出错、最难把握与确定的是判断两个命题之间的相互关系，即充分与必要条件。在此，我们针对简易逻辑问题总结、分析了经常困扰同学们的七类典型错误，以帮助同学们认识，并掌握解答它们的正确方法与过程。以期达到以悟治误的目的。

一、不能正确认识方程与根的关系导致命题错误

例1判断命题“方程x2-3x+2=0的根是x=1”的真假。

错解：真命题。

错因分析：命题“x=1是方程x2-3x+2=0的根”与命题“方程x2-3x+2=0的根是x=1”是两个不同的命题，前者为真命题，后者为假命题。

正解：假命题。因为方程x2-3x+2=0的根是x=1 或x=2，而不是只有一个根x=1。

二、不理解否命题及否命题与其他命题的关系导致错误

例2写出命题“若x2+y2=0，则x=0且y=0”的否命题，并判断真假。

错解1：否命题：若x2+y2≠0，则x ≠0且y≠0。

错因分析：且的否定为或，x=0且y=0的否定为x≠0或y≠0。

错解2：原命题为真，所以否命题为假。

错因分析：原命题与否命题的真假没有关系。

正解：否命题：若x2+y2≠0，则x≠0或y≠0，所以否命题是真命题。

三、不能正确区分前提条件与命题条件导致表述命题错误

例3将下面的命题写成“如果p，则q”的形式：当a＞0时，函数y=ax+b 的值随x 的增大而增大。

错解：“如果p，则q”的形式为：如果a＞0，则函数y=ax+b的值随x 的增加而增加。

错因分析：原命题有两个条件：a＞0 和x 增加，其中a＞0是大前提，x 增加是条件。

正解：“如果p，则q”的形式为：当a＞0时，如果x 的值增大，则函数y=ax+b的值也增大。

四、对含有一个量词的命题否定不完全致误

例4已知命题p：存在一个实数x0，使得-2＜0，写出¬p。

错解一：¬p：存在一个实数x0，使得x0-2≥0。

错解二：¬p：对任意的实数x，都有x2-x-2＜0。

错因分析：写含有一个量词的命题的否定，首先要明确这个命题是全称命题还是特称命题，并找出其量词的位置及相应结论，然后把命题中的全称量词改成存在量词，存在量词改成全称量词，同时否定结论。

正解：¬p：对任意的实数x，都有x2-x-2≥0。

五、对命题的否定形式认识错误导致误判命题间的相互关系

例5已知命题p：|5x-2|＞3，命题q：，那么¬p 是¬q 的什么条件?并写出解答过程。

错解：许多同学认为¬p 与¬q 分别是

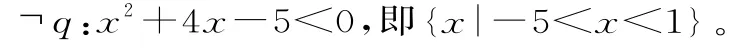
于是¬p 既不是¬q 的充分条件也不是¬q 的必要条件。

错因分析：错误的根源在于当p 与q 是不等式时，对¬p 与¬q 的形式在认识上存在错误。实际上¬p 与¬q 是对不等式|5x-2|＞3与解集的否定。正确的解答应该是先把这两个不等式的解求出，对其解集进行否定。

正解：由不等式|5x-2|＞3，可得

六、不能正确认识参数范围与命题间的真假关系导致求参数取值范围出错

例6已知p：方程x2+mx+1=0有两个不等的负根；q：方程4x2+4(m-2)x+1=0无实根。若“p 或q 为真，p 且q 为假”，求m 的取值范围。

错解：若方程x2+mx+1=0 有两个不等的负根，则有解得m ＞2，即p：m＞2。

若方程4x2+4(m-2)x+1=0无实根，则有Δ=16(m-2)2-16=16(m2-4m+3)＜0，解得1＜m＜3，即q：1＜m＜3。

故m 的取值范围是2＜m＜3。

错因分析：以上所解得m 的范围m ＞2与1＜m ＜3，是将实数集分成了四个部分。不少学生对每一部分的含义不清晰。误把m＞2与1＜m＜3的公共部分2＜m＜3，当成所求m 的取值范围。

正解：若方程x2+mx+1=0 有两个不等的负根，则有解得m ＞2，即p：m＞2。

若方程4x2+4(m-2)x+1=0无实根，则有Δ=16(m-2)2-16=16(m2-4m+3)＜0，解得1＜m＜3，即q：1＜m＜3。

因为“p 或q 为真”，所以p，q 中至少 有一个是真命题。又“p 且q 为假”，所以p，q中至少有一个是假命题。

因此，p，q 两个命题应该是一真一假，即“p 为真，q 为 假”或“p 为 假，q 为 真”。当m∈(-∞，1]时，p 假，q 假；当m∈(1，2]时，p假，q 真；当m∈(2，3)时，p 真，q 真；当m∈[3，+∞)时，p 真，q 假。

七、没有正确理解“或”与“且”导致判断两个命题之间的关系出错

例7若非空集合M ⊂N，则a∈M 或a∈N 是a∈(M ∩N)的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

错解：a∈(M ∩N)的意思是a∈M 且a∈N，所以a∈M 或a∈N 不能推出a∈(M∩N)，同样a∈(M ∩N)也不能推出a∈M或a∈N，所以a∈M 或a∈N 是a∈(M ∩N)的既不充分也不必要条件。故选D。

错因分析：“或”与“且”理解错误，逻辑中的“或”与生活中的“或”有区别，a∈M 或a∈N 包括三种：a∈M 但a∉N；a∈N 但a∉M；a∈M 且a∈N。所以a∈(M ∩N)可以推得a∈M 或a∈N。

正解：a∈(M ∩N)的意思是a∈M 且a∈N，而a∈M 或a∈N 包括三种：a∈M 但a∉N；a∈N 但a∉M；a∈M 且a∈N。所以a∈M 或a∈N 不能推出a∈(M ∩N)；a∈(M∩N)可以推得a∈M 或a∈N。故选B。