会当凌绝顶一览众山小———复数常见错例剖析

■陕西省韩城市西庄中学 张 斌

复数在各类考试中主要以考查基本概念、基本计算与其他知识相结合为主的客观题形式出现，难度低，重基础。学习中只要夯实基础，把握复数的概念、复数相等的充要条件、复数的四则运算、虚数单位i的周期性，针对不同试题，采取不同的求解策略，解题时才会得心应手。

一、对复数概念的考查

复数的概念在考试中常出现的类型有：(1)复数概念的辨析；(2)复数的有关分类；(3)复数相等条件的应用；(4)复数与复平面内点的对应关系。

例1下面四个命题中正确命题的个数是( )。

①0比-i大；②两个复数互为共轭复数，当且仅当其和为实数；③x+yi=1+i的充要条件为x=y=1；④如果让实数a 与ai对应，那么实数集与纯虚数集一一对应。

A.0 B.1 C.2 D.3

错因分析：本题考查复数的基本概念，常见错误就是对概念理解不到位，对复数分类分析不到位。

正解：①复数集内不全是实数的数不能比较大小；②2+3=5∈R，但2，3不是共轭复数；③只有当x、y∈R 时，才有x=y=1；④若a=0，则0i=0不再是纯虚数。

答案：A

例2当m 取何实数时，复数z=

错因分析：由于所给复数z 已写成标准形式，即z=a+bi(a，b∈R)，所以只需按题目要求，对实部和虚部分别进行处理，就极易解决此题，但要注意条件同时满足才能成立，不能将条件分开求解。

正解：根据复数的概念知，当z 为实数。

所以当m=5时，z 是实数。

例3已知x 是实数，y 是纯虚数，且满足(2x-1)+i=y-(3-y)i，求x 与y的值。

错因分析：因为y 是纯虚数，所以可设y=bi(b∈R，且b≠0)，代入等式，把等式的左、右两边都整理成a+bi的形式后，再利用复数相等的充要条件得到关于x 与b 的方程组，求解后得x 与b 的值。

正解：设y=bi(b∈R，且b≠0)，代入条件并整理得(2x-1)+i=-b+(b-3)i。

例4已知复数z1=3+i，z2=1-i，则z=z1·z2在复平面内的对应点位于( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

错因分析：本题考查复数代数形式的乘法运算，以及复数与复平面内点的一一对应关系，计算时要将对应符号包括在内，则由z1·z2=(3+i)·(1-i)=4-2i，知对应点为(4，2)，位于第一象限。

正解：因为z1·z2=(3+i)·(1-i)=4-2i，所以对应复平面上点为(4，-2)，所以复数z 对应的点应在第四象限。

答案：D

二、复数的有关计算

复数的计算在高考题目中都会出现，并且每道题目都会汇聚复数的四种运算，这就要求我们熟悉四种运算法则仔细操作。

例5是虚数单位)等于( )。

A.1+i B.-1-i

C.1+3i D.-1-3i

错因分析：本题考查复数代数形式的基本运算。可利用多项式乘以多项式的方法解决此类问题，但应特别注意运算过程中的符号问题。

正解

答案：D

三、虚数单位i的计算

若i2=-1，则称i为虚数单位，与i有关的幂的计算一直是各类考试的重点内容，解决这类题的关键是要掌握i的周期性。

例6设z=_____。

错因分析：本题考查i的周期性及常见复数的化简，记不清指数关系容易出错，必须记清如(1±i)2=等。

正解：z=

答案：-1-i

四、共轭复数的性质及应用

例7(2019年陕西西安联考试题)设i是虚数单位表示复数z 的共轭复数，若z=1+i，则

A.-2 B.-2i C.2 D.2i

错因分析：本题需要理解复数与共轭复数之间的关系，利用代数关系代入进行计算，容易出现计算上符号的错误。

正解：由

答案：C

五、与复数有关的变式应用

此类问题主要是对复数有关知识的深层挖掘，题目涉及复数的几何意义、模的有关计算、与复数有关的创新题目等。

例8已知复数Z 满足|Z|=2，求|Z-i|的最值?

错因分析：该题解法很多，既可以由模的定义转化为三角函数的最值。甚至可以由||Z1|-|Z2||≤|Z1±Z2|≤|Z1|+|Z2|进行放缩，但运算要么过于烦琐，要么取等号时条件验证较困难，各有利弊，但仔细审题将模的条件视为距离，结合“|Z-Z0|=a 表示Z所对应点的轨迹是以Z0所对应点为圆心，以a 为半径的圆；|Z-Z0|表示Z 所对应点到Z0所对应点之间的距离”进行求解。

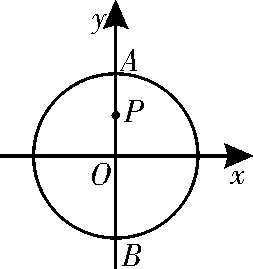
图1

正解：由|Z|=2 知复数Z所对应复平面上点的轨迹是以原点为圆心，以2 为半径的圆。而|Z-i|是求Z 所对应点到点P(0，1)之间的距离。

如图1 所示，显然有|Zi|min=|PA|=1，|Z-i|max=|PB|=3。