用好习题，促进学生几何推理能力发展

吴晓霞

习题是对课堂学习内容的巩固和补充，它不仅是知识和技能的载体，更是能力与思维训练的原动力。在“图形与几何”领域的教学中，由于小学生的年龄特征和思维方式，几何推理的能力较薄弱。这要求教师在对教材习题进行选择和运用时，应有充分的认识和理解。以下是笔者在实践中的几点思考。

一、先形后数，逐步发展几何推理能力

先形后数就是先从形的感知再到数的计算，更符合小学生数学学习的思维习惯。直观估测，可以很好地帮助学生发展空间想象能力;再到数的计算，让形象思维逐步向抽象思维过渡，从而发展几何推理能力。

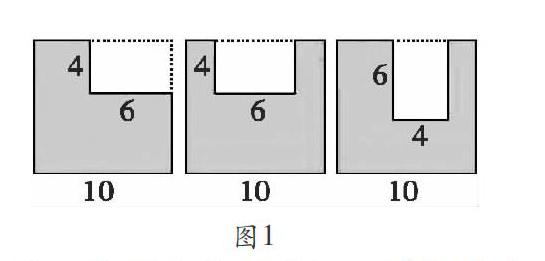
例如，人教版教材三下第69页的第10题，这是一道解决从一个图形中剪掉一部分，求所剩图形（图1）面积和周长的习题。如果不计算，在视觉的直观性上，容易影响学生对所剩图形面积、周长大小的准确判断。于是笔者重组了习题，先隐去图1中的数据，淡化“算”的痕迹，从形上直观感知所剩部分的面积大小。此时，有学生凭直觉估测教材习题左图中剩下的部分多，所以面积大。也有学生认为中图剪去的部分虽然位置不同，但方向、大小与左图一样，因此估测剩下的面积大小一样。也有学生坚信三幅图剩下部分的面积都一样大，认为从同样大小的正方形中剪去同样大小的一部分，所剩面积肯定也一样大。随后，笔者再还原数据信息，鼓励学生通过计算验证猜想。学生得出算法1：S-S=S;算法2：将剩下的不规则图形转化为几个规则的圖形，再求剩下面积。学生通过计算发现：面积是可以直接相加减的;从同样大小的图形中去掉同样大小的一部分，所剩面积相等，与图形的形状无关。笔者最后顺势而导：“剩下图形的周长会相等吗？”帮助学生进一步巩固周长的概念，同时还建立起了面积与周长之间的联系，层层深入探究，完善知识结构，理解当面积相等时，周长不一定相等。

二、从摆到推，动态发展几何推理能力

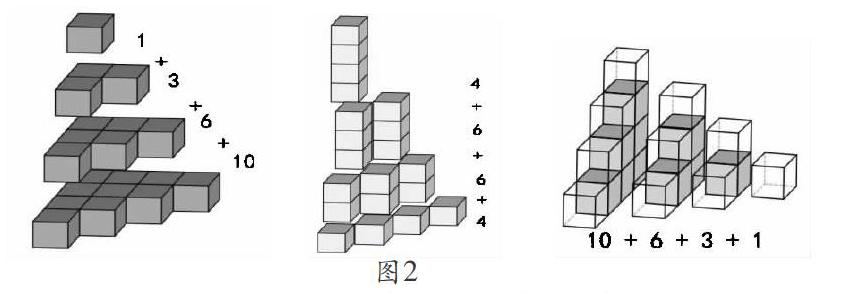
动手拼摆是学习数学的重要活动方式，对于小学生学习图形与几何知识，培养空间想象能力是十分有益的。例如，人教版四下“观察物体（二）”的内容，教材中第16页的第7题，要求根据组合体图形，确定正方体的数量。

此题难点在于如何确定被遮挡部分的正方体数量。教学时，笔者先引导学生从静态的观察开始，通过不同的角度观察，将立体图形转化成平面图形，在大脑中形成完整的表象;接着鼓励学生动手拼搭，一边探究怎样摆，一边想象组合体的实际构造;再运用信息化手段动态辅助教学，让学生更直观理解和验证所想;最后有序推理出正方体的确定数量。

从摆到推，动态的教学很好地解决了学生空间想象能力和理解水平参差不齐的问题。在直观拆解组合体（如图2）时，“被遮挡”的地方可视化后，学生更能够充分理解组合体的实际构造，从而发现规律归纳方法，引导思维从无序走向有序，动态中有效提升几何推理能力。

三、知行明理，理性发展几何推理能力

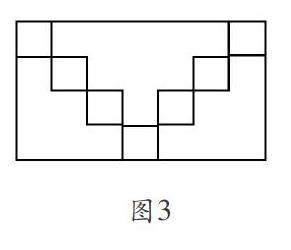
知行明理是指数学学习时不仅要知其然，还要知其所以然，不能仅仅停留在“是什么”的层面，还要知道“为什么”和“怎么样”。如在一次讲座中，笔者见到如下一道题：下面长方形（图3）里，每个小正方形的边长都是1厘米，你知道长方形的面积吗？并说说你的理由。

有的学生认为把空白的地方用同样面积大小的小正方形填满，长方形中有几个小正方形，面积就有多大。运用相同面积单位密铺的办法，把若干面积单位进行累加，从而求出长方形的面积。有的学生认为可以通过平移小正方形，实现将长方形的“长”转化为7个小正方形边长之和，“宽”转化为4个小正方形的边长之和，由此计算出长方形的面积。这是借助了面积度量的方法，探寻小正方形边长与长方形长、宽的关系，明确每行个数与行数以及面积单位总个数之间的关系，真正理解面积度量的本质，避免了生搬硬套计算公式。此题还可以继续往下探究：如果挖去这样7个小正方形后，能计算剩下阴影部分的面积和周长吗？这样创编的习题既有趣又充满挑战。

为了避免僵化地考查学生对公式的运用，应带着思考而学，在层层深入的练习活动中，渗透数学的思维和方法。更重要的是给学生提供积累数学活动经验及解决数学问题的机会，知行明理，关注知识背后的道理，回归数学的本质，唯有这样，才能理性地提升几何思维，有效地发展推理能力。

四、思辨求新，严谨发展几何推理能力

严谨的数学思维，是指思考问题符合逻辑、严密、有根据。严谨思维的习得，可以打破思维定势的枷锁，在思辨中求新，使考虑问题更周密。

比如，人教版三上第87页的第4道习题。学生在解决此道问题时，大部分是直接应用教材中例题5的知识，解答花边长为36分米的长方形周长最短。当笔者追问他们是怎么想时，思维定势的“痕迹”呈现出来：已知当长方形的长和宽越接近时，周长就越短。因此，学生在汇报作品拼摆的方法时，无一例外呈现的都是长方形的摆法。在比较优化方法时，学生提出第一种是每行摆18幅，摆1行，求出花边长是76分米，这样既不美观也摆不下，不符合生活实际。有的学生提出第二种方法：每行摆9幅，摆2行，花边长是44分米。也有的认为第三种方法最优：每行摆6幅，摆3行，花边长是36分米。这样花边的长和宽的长度最接近，且花边总长在这三种方案中是最短的，符合题意。

此时笔者先是肯定学生的想法，但是有意识地追问：“还有没有其他摆法呢？”并引导学生再次读题时，让学生明确题目并没有要求要拼摆成长方形或正方形时，再次组织学生进行小组讨论。于是新的拼摆策略“诞生”了，而且周长也是36分米。

学生通过推理归纳得出：只要拼摆后隐藏在图形内部的小正方形的边长越多，露在外面的边长就越少，图形的周长也就越短。

总之，教师应让推理作为探索数学思路的工具、作为数学严谨求证的手段，让学生在丰富的数学活动中积累经验，循思而练，带思而学，有效地促进几何推理能力的发展。

（作者单位：福建省福州市温泉小学   本专辑责任编辑：王振辉）