主动油气悬架电液伺服系统的自适应滑模控制

刘 爽，李 硕，赵丁选，高 浩

(1.燕山大学 河北省工业计算机控制工程重点实验室，河北 秦皇岛 066004；2.燕山大学 机械工程学院，河北 秦皇岛 066004)

0 引言

悬架作为车辆的重要组成部分之一，是连接车身与车轮的纽带，对于车辆正常行驶具有非常重要的作用[1-3]。油气悬架是悬架从使用介质上的一个分类，但是从控制力的角度划分，人们一般把油气悬架归为被动悬架，这是因为油气悬架一般不涉及控制力，主要是气囊和结构的变化。为了进一步改善油气悬架的使用性能，提高悬架的适应能力，研究人员提出了主动油气悬架的概念[4-5]，使得通过伺服阀对油气悬架的油路进行动力控制成为了新的发展方向。

在当前油气悬架的研究方面，人们侧重于研究建立合理的非线性悬架模型对车辆的振动响应进行比较精确的分析和预测。例如么鸣涛等人[6]提出了应用微分几何理论并经过非线性状态反馈变换的方法对半主动悬架非线性系统进行精确线性化。LI Weiping等[7]通过适当的坐标变换和反馈控制，实现非线性油气悬架系统的精确线性化。 Deprez K[8]和Herrnberger M[9]在建立模型的过程中重点考虑了模型结构的特性，使模型更加接近工程实际。目前大多数学者都专注在油气悬架的模型结构上，致力于研究新型的悬架结构，建立更加合理的非线性物理模型，对于油气悬架进行主动控制研究较少。

在悬架的主动控制研究方面，自适应控制和滑模控制由于具有强鲁棒性，能够有效地处理非线性、参数不确定性和外加干扰对悬架的影响，尽可能地满足悬架的性能要求而被大家广泛使用。Xiao L[10]研究了一种基于滑模控制的单杆电液执行机构的力控制问题，通过对伺服阀的建模，并依据万达定律对系统设计滑模控制器，仿真验证了所提出的单杆电液执行机构级联滑模力控制方法的有效性。Avas Y等[11]通过对伺服阀的建模，利用自适应反步控制方法，使设计的控制器在具有参数不确定的情况下，悬架系统依然能够提高系统的稳定性和平顺性。 Sun W等[12-13]针对非线性不确定悬架系统，建立伺服阀的非线性模型，通过对伺服阀的自适应振动控制，使悬架系统的垂直运动和俯仰运动均保持稳定，从而提高了悬架系统的平顺性。Lin J等[14]针对簧载质量速度设计增强型模糊滑模控制器，不仅提高了车辆行驶的平顺性，而且提高了车辆行驶的舒适性。

虽然文献[10-14]在建模过程中考虑了伺服阀的建模，但是它们更加侧重于控制器的设计，对于悬架本身的建模比较简单，对于系统的刚度和阻尼都是使用线性模型，这样虽然能够得到较好的控制效果，但汽车非线性因素[15-16]在一定的载荷、激励和频域内对悬架的影响十分突出，影响着悬架的性能。并且车辆在行驶过程中，会受到外部未知扰动的影响[17]，这些都需要综合考虑。

综上所述，本文建立了主动油气悬架非线性动力学模型，在考虑电液伺服系统的基础上针对不确定的系统刚度设计出相应的自适应律，同时考虑不确定的外部扰动对悬架系统进行滑模控制，并利用饱和函数的性质减弱切换控制对系统的抖振影响。仿真结果表明，本文设计的自适应滑模控制器，能够应对系统不确定参数和外部未知扰动的影响，且提高了车辆行驶的平顺性、乘坐舒适性和安全性。

1 主动油气悬架模型

根据文献[18]建立油气悬架的被动悬架模型。该模型动力学模型可以描述为

(1)

式中，ms为簧载质量，mu为非簧载质量，kt为轮胎刚度系数，z0为路面输入，zu为非簧载质量的位移，zs为簧载质量的位移，Fk为非线性弹性力，Fc为非线性阻尼力。

(2)

式中，z为活塞杆的相对位移，Cd为阻尼孔、单向阀的流量系数，ρ为液压油密度，AZ为阻尼孔的等效截面面积，AD为单向阀的等效截面面积，A1为双气室油气悬架Ⅰ腔截面积，A2为油气悬架Ⅱ腔截面积。

在被动油气悬架的基础上，通过改变油气悬架的结构，增加伺服阀和液压源等主动控制部件，将被动油气悬架转换为主动油气悬架，其模型示意图如图1所示。

图1 主动油气悬架模型Fig.1 Active hydro-pneumatic suspension model

考虑到实际主动力由液压系统提供，并受伺服阀控制。根据文献[19]，则伺服阀的特性方程为

(3)

式中，A为活塞的有效面积；pL为活塞上下两侧的压力差；vt为液压缸总容积；βe为液体弹性模量；kq为伺服阀流量增益；kce为伺服阀流量压力系数，u1为阀芯位移。

主动油气悬架主要依靠液压泵产生液压差来提供主动力。由于在相同条件下，气体比液体具有更大的压缩性，一般都在1 000～10 000倍之间，因此进行主动控制后系统的刚度主要为液压刚度，系统的刚度大大增加；又因为液体不容易被压缩，其可压缩性为钢的50～100倍，因此进行主动控制后的系统刚度可以看成常数。由于液体泄漏和储能器中的气体的缘故，又使得这个常数具有不确定性，会在一个范围内进行波动，但是系统的阻尼孔并没有发生变化，液压缸还是原来的阻尼系统。因此，由节流小孔理论可知，系统阻尼仍然存在，且与簧载质量和非簧载质量的相对速度呈现非线性关系。模型可进一步改写为

(4)

式中，k为具有不确定性的刚度系数，Fc为非线性阻尼力且与式(2)相同。

2 控制器设计

(5)

式中，参数θ有界，即θmin<θ<θmax，Fs为系统外部的不确定因素所造成的扰动，扰动如果无限大则会造成对悬架系统的破坏，因此为了仿真的方便性假设FS有界，且|FS|≤D，D为一个固定常数，且

针对主动油气悬架中的伺服阀建模，并考虑系统外部干扰以及参数的不确定性，应用滑模控制的切换控制思想与自适应控制相结合的控制策略设计控制器，使系统既能保持稳定又可以对干扰和参数不确定性具有鲁棒性。

定义系统位置误差为

(6)

对上式求导可得

(7)

定义系统第一个李雅普诺夫函数为

(8)

对上式求导得

(9)

取控制中间变量为

z2=x2+ξ(x1-x3)+c1z1，

(10)

式中，c1>0为常数，下文中的c2，c3都为大于0的常数，则

(11)

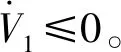
(12)

定义系统第二个李雅普诺夫函数为

(13)

对上式求导可得

(14)

令

e5=x5-x5d,

(15)

式中，x5d为虚拟控制量，取

(16)

式中，c2为正实数，则

(17)

定义系统李雅普诺夫函数为

(18)

对上式进行求导可得

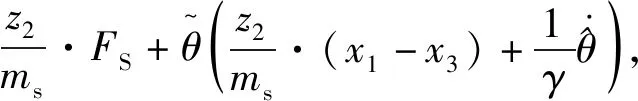
(19)

令

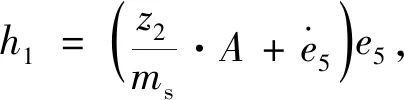
(20)

对式(20)展开得

(21)

系统控制律包括等效控制和切换控制，取控制律为

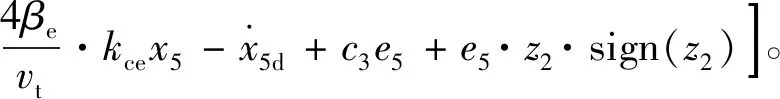
(22)

在滑模控制器设计过程中，利用符号函数sign(x)来应对外部扰动的影响，但同时会引起系统的抖振问题，因此为了改善抖振问题，这里把符号函数变为饱和函数sat(x)，

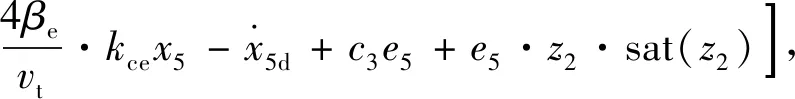
(23)

取相应的投影自适应律为

(24)

式中，

则有

(25)

对式(25)进行有条件的缩放，由于FS有界，且FS≤D。为了说明方便，选取参数c1+ξ=c2=c3=α/2(当然也可以不这样选取，只要取c1+ξ、c2、c3中最大或比这三个数还大的为α/2即可)，则式(25)可以改写为

(26)

根据引理1进一步对式(26)进行化简。

(27)

由上述引理1可得

(28)

下面对系统的零动态稳定性进行证明。

令输出y≡0，得到系统的零动态方程：

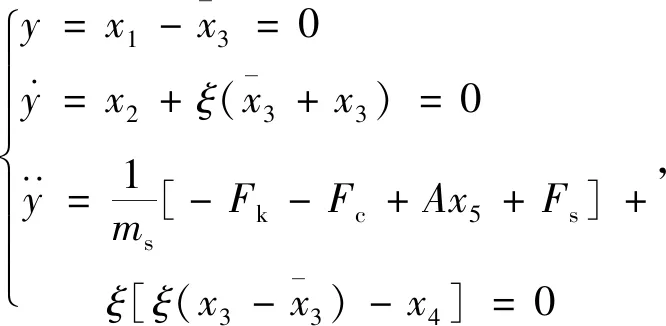
(29)

把上式带入式(5)可得

(30)

把上式改写成矩阵的形式为

3 仿真分析

系统参数如表1所示。利用MATLAB/Simulink对系统进行控制仿真。

表1 悬架系统参数Tab.1 Suspension parameters

仿真时控制器参数及自适应律各参数为：c1=1，c2=0.8，c3=16，θ=1.2×106，θmin=1.15×106，θmax=1.25×106，γ=1×1010。

路面输入采用随机路面输入，波形如图2所示。本次随机路面选取为速度v=20 m/s，B级路面，随机白噪声均值为0，强度为1，下限截止频率取f0=0.006 28 Hz。本文中外部扰动信号取为FS=40 sin(8πt)，波形如图3所示。在随机路面的激励下，考虑系统参数的不确定性以及外部扰动进行控制器仿真，所得的曲线如图4～6所示，通过求解功率谱密度可以分别得到各曲线的功率谱密度曲线，结果如图7～9所示。

图4为车身垂直加速度关系曲线图，从图中可以看出主动油气悬架的车身垂直加速度明显降低，车身平顺性得到了明显改善；图5为悬架动行程关系曲线图，从图中的对比可以发现，主动油气悬架比被动油气悬架具有更低的悬架动行程；图6为车轮动载荷关系曲线，根据曲线可以发现主动油气悬架的动载荷更低，行车更安全。

图7为车身垂直加速度功率谱密度曲线，从图中可以看出主动悬架与被动油气悬架相比，车身垂直振动能量明显降低。

图2 随机路面输入Fig.2 The random road input

图3 干扰输入Fig.3 The disturbance signal

图4 车身垂直加速度Fig.4 Sprung mass acceleration

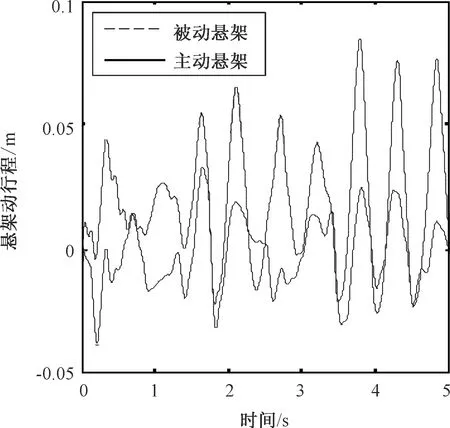
图5 悬架动行程曲线Fig.5 Suspension relative displacement

图6 车轮动载荷曲线Fig.6 Dynamic tire load

图7 车身垂直加速度功率谱密度Fig.7 Vertical acceleration PSD

图8 悬架动行程功率谱密度Fig.8 Suspension travel PSD

从图8的悬架动行程功率谱密度曲线可以看出主动油气悬架动行程的振动能量方面减弱的非常明显。图9为车轮动载荷功率谱密度曲线，根据曲线可以发现主动悬架的振动能量明显降低，有力地证明了主动悬架的优势。

下面通过均方根值进一步说明主动悬架的优势。表2所示为随机路面悬架性能评价指标均方根值(RMS)。

从表2可以看出，在随机路面的输入下，主动油气悬架的性能在垂直加速度和车轮动载荷方面相比于被动油气悬架提升巨大，都在68%以上，而悬架动行程变化则相比提升50%多，性能提升也比较明显。

综合图4至图9及其表2的相关分析，在20 km/h的车速的路面输入下，即使存在参数不确定性以及外部未知扰动，主动悬架的车轮动载荷、车身加速度以及悬架动行程相比被动悬架都有了极大的改善，从频域图中可以看出悬架系统的振动能量大幅度降低，说明控制取得了非常好的效果。同时时域的分析也印证了频域上的结果，即车轮动载荷、悬架动行程和车身加速度在控制器的作用下提升非常明显，显示了主动控制的极大优越性。

4 结论

本文对伺服阀控制下的油气悬架进行了主动控制研究。在考虑油气悬架作动过程中刚度和阻尼非线性变化，建立了油气悬架的非线性动力学模型。并针对电液伺服系统的动力学特性以及外加未知扰动的情况，给出了悬架的自适应滑模控制方法，有力地解决了刚度参数的不确定性对系统造成的影响，同时采用滑模控制的切换控制方法提高系统对外界干扰的抑制能力，并通过饱和函数代替符号函数解决了控制过程中的抖振问题。仿真表明本文提出的自适应滑模控制器能有效提高车辆驾驶的平顺性、乘坐舒适性和操作安全性，为指导工程应用提供了有效途径。