利用研究性学习 提升学习能力
——“竖直平面圆周运动”专题的研究案例分析
2020-01-01■郭磊
■郭 磊
研究性学习是全面培养学生综合运用所学知识的能力、收集和处理信息的能力、分析和解决问题的能力、语言文字能力,以及团结协作能力的重要环节。这种方法还有利于培养学生独立思考的习惯,激发学生的创新意识。
在高三的专题复习过程中,对于“竖直平面圆周运动”这个知识点,同学们可以先在小组合作中突破重难点,在大家都参与的知识点的生成过程中,弄清怎么把多个知识点整合到一起。具体做法是先围绕本专题所要解决的问题去挖掘一些问题并进行研究、探讨,对存在障碍的问题应及时解决,通过小组内成员的共同努力和协作,将所提出的问题一个个解决;再将问题的结果进行归纳和总结,完成这个专题的复习目标。下面将这个专题中的一个知识点的复习过程展示如下。
专题内容:竖直平面内圆周运动的临界问题。
模型设计:三大模型,即绳球模型、杆球模型、管道模型。
特殊位置:竖直平面内圆周运动的最高点和最低点。
知识储备:分别根据三大模型的特点,画出小球在最高点和最低点的受力示意图,并结合受力示意图,写出向心力的关系式。注意两个问题,一是杆球模型和管道模型中,小球在最高点的受力情况分成两种情况;二是小球在最高点和最低点这两个特殊位置时,小球速度大小的关系,动能定理的使用。

图1
问题一:如图1所示,长为L的轻杆一端固定着一质量为m的小球,使小球在竖直面内做圆周运动。
(1)当小球在最高点B的速度为v1时,求轻杆对小球的作用力。
(2)轻杆拉小球过最高点的最小速度为多少?
(3)试分析光滑圆管竖直轨道中,小球过最高点时受管壁的作用力与速度的关系。
解:(1)设轻杆对球的作用力向下,则。当v1=时,F=0;当时,F>0,表示小球受到轻杆的作用力方向向下,表现为拉力;当时,F<0,表示小球受到轻杆的作用力方向向上,表现为支持力。
(2)由(1)中的分析可知,轻杆拉小球过最高点的最小速度为零。

图2
(3)如图2所示,设管壁对小球的作用力向下,为N,则,得N=。当时,N>0,即上管壁对小球有向下的压力;当时,N<0,即N竖直向上,下管壁对小球有向上的支持力。
【总结】细杆和管形轨道模型:
1.最高点的最小速度。
如图3所示,细杆上固定的小球和管形轨道内运动的小球,因为杆和管在最高处能对小球产生向上的支持力,所以小球恰能到达最高点的最小速度v=0,此时小球受到的支持力N=mg。
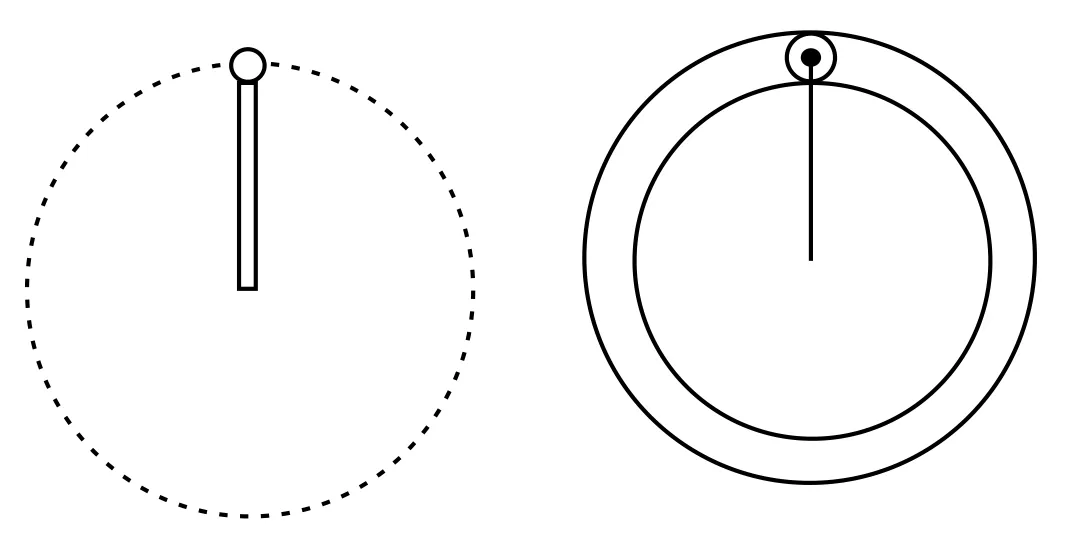
图3
2.小球通过最高点时,细杆或管形轨道对小球的弹力情况。
(1)杆或管的外侧对小球产生向下的拉力或弹力时,F随v的增大而增大。
(2)小球在最高点只受重力时,不受杆或管的作用力,即F=0。
(3)杆或管的内侧对小球产生向上的弹力时,F随v的增大而减小。
3.小球能过最高点的条件:v≥0。

图4
问题二:如图4所示,一摆长为r的单摆,摆球的质量为m,要使摆球能在竖直平面内做完整的圆周运动,那么摆球在最低点的速度v0至少为多大?

图5
解:小球在最高点受重力mg和绳的拉力T,如图5所示,由牛顿第二定律得,因为m、r一定,所以v越小,T也越小。当T=0时。
讨论:(1)如果把题中的摆绳去掉而改为与半径与摆长相同的圆环,使小球沿环内侧做圆周运动,那么情况又如何?
(2)如果在(1)的基础上,使小球不脱离圆环轨道运动,则小球在最低点的最小速度为多少?
分析:若将绳变成圆环,在圆环的最高点,因为小球是沿环内侧运动,环给小球提供支持力的方向是竖直向下的,和原题中绳在最高点的拉力情况一致,所以解决过程和原题是一致的。
在讨论(2)中,同学们在理解小球不脱离圆环轨道这一要求时,容易只考虑小球做完整的圆周运动这一种情况,而忽略当小球运动到和圆心位置等高的点,速度减为零时,将不会继续向上运动,而是沿圆环轨道滑下的情况。
