广义结式矩阵核维数的证明*

杨 翠 芝

(安徽大学 数学科学学院，合肥 230601 )

结式矩阵的研究开始于19世纪中期，因其在线性系统、稳定性理论、控制性理论等问题中都起着重要作用，因此备受关注.文献[1]讨论了经典的Sylvester结式矩阵与Bezout矩阵的关系，并给出了经典的Sylvester结式矩阵的算子表示；文献[2]讨论了两个多项式的最大公因式与Sylvester结式矩阵的联系，给出了两个多项式的最大公因式的次数与Sylvester结式矩阵秩之间的等式关系.此处在文献[2]的基础上讨论广义结式矩阵与多项式之间的关系，给出并证明了两个多项式的广义结式矩阵核维数.

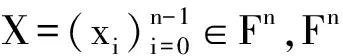
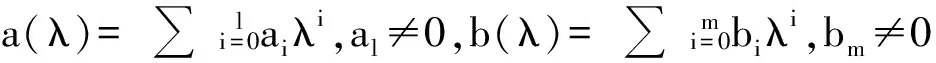
很显然，两个多项式的经典Sylvester结式矩阵是(m+n)×(m+n)的方阵.

定义1 设F为代数闭域，令U∈Fn+1,V∈Fm+1,p≤min{m,n}，假设m,n≥0，则广义结式矩阵定义为

特别地,当p=0时，Resp(U,V)称为经典的Sylvester结式矩阵.

则(Dm,m+n(W)TX)(t)=W(t)X(t).

引理2 令q∈Fm+n,w∈Fn+1,p∈Fm,那么Dm,n+m(w)qJ=pJ,当且仅当存在p1,p2∈Fn使得w(t)q(t)=p1(t)+p(t)tn+tm+np2(t)成立.

证明由矩阵的运算有等式(1)成立：

(1)

则

(2)

将式(2)最后一个等式两边同乘以Jm，即

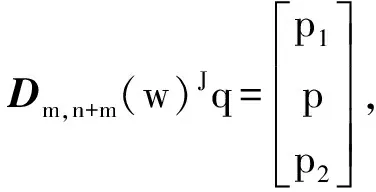
证明取qJ∈kerDn+m-p-υ,n+m-p(w),则q∈Fn+m-p,由引理2,存在p1,p2∈Fυ使得

w(t)q(t)=p1(t)+tm+n-pp2(t)

(3)

式(3)两边分别乘以U0(t),V0(t)得

u(t)q(t)=u0(t)p1(t)+tn+m-pu0(t)p2(t)，v(t)q(t)=v0(t)p1(t)+tn+m-pv0(t)p2(t)

由于degU0(t)≤n-υ,degV0(t)≤m-υ， 由引理2得

qJ∈kerDm-p, n+m-p(u),qJ∈kerDn-p,n+m-p(v)

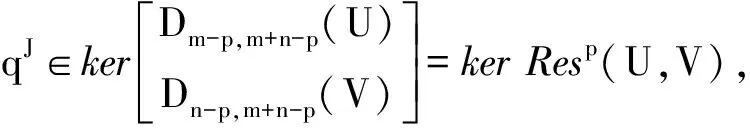
1Dn+m-p-υ,n+m-p(w)⊆ker Resp(U,V)

定理2 设Resp(U,V)是给定多项式U(t),V(t)的广义结式矩阵，则

(i)dimker(Resp(U,V))T=max{0,υ-p}；

(ii)dimker Resp(U,V)=max{υ,p}.

证明

(i)

(4)

由引理1，式(4)转化成

U(t)X(t)+V(t)Y(t)=0，X(t)∈Fm-p[t],Y(t)∈Fn-p[t]

(5)

则

W(t)(U0(t)X(t)+V0(t)Y(t))=0⟹(U0(t)X(t)+V0(t)Y(t)=0⟹U0(t)X(t)=-V0(t)Y(t)

(6)

因为U0(t)|U0(t)X(t)，所以U0(t)|-V0(t)Y(t)，因为u0(t)与V0(t)互素，所以U0(t)|Y(t).设Y(t)=U0(t)P(t)，由于U0(t)∈Fn-υ+1[t],Y(t)∈Fn-p[t],所以

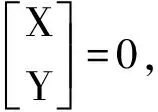
2) 当υ

其中U0(t)是生成的多项式)

(7)

(3)

1) 当υ≥p时，由(i)可知dimker(Resp(U,V))T=υ-p，所以

rank Resp(U,V)T=m+n-2p-(υ-p)=m+n-p-υ

dimker Resp(U,V)=m+n-p-rank Resp(U,V)=m+n-p-rank(Resp(U,V))T=υ

2) 当υ

rank(Resp(U,V))T=m+n-2p

dimker Resp(U,V)=m+n-p-rank Resp(U,V)=m+n-p-rank(Resp(U,V))T=p

综合(ii)的1)，2)，知dimkerResp(U,V)=max{υ,p}.

参考文献：

[1] FUHRMANN P A. A Polynomial Approach to Linear Algebra [M]. New York:Sprigner-Verlag,1996

[2] BANETT S. Polynomials and Linear Control Systems[M]. New-York：Marcel Dekker ,1983

[3] 刘冰，张羽乾. Bernstein-Bezoutian矩阵的若干性质[J]. 重庆工商大学学报：自然科学版，2011,28(4):339-442

[4] 王其林.关于“正交矩阵的特征多项式及特征根”的注[J]. 重庆工商大学学报：自然科学版，2011(4)：154-155

[5] 陈公宁.矩阵理论与应用[M]. 北京：高等教育出版社，1990

[6] CHEN G N, ANG Z H. Bezoutian Representation via Vandermonde Matrices[J]. Linear Algebra Appl,1993(186)：35-46

[7] HEINING G , ALVAREZ M. On Bezoution Reduction with Vandermonde Matrices and Operators [J]. Operator Theory, 1984(13)：100-121

[8] FUHRMANN P A. On Bezoutian Vandermonde Matrices and the Lienard-Chipart Stability Criterion [J]. Linear Algebra Appl ,1989(120)：25-33