EWT与加权多邻域粗糙集结合的旋转机械故障特征提取方法
2019-12-31吴耀春赵荣珍靳伍银
吴耀春, 赵荣珍, 靳伍银
(1.兰州理工大学 机电工程学院,兰州 730050; 2.安阳工学院 机械工程学院,河南 安阳 455000)
旋转机械是一类广泛使用的动力设备,因此对其实施智能化运行维护管理的意义重大[1]。然而复杂的结构型式以及动态运行环境,使得此类设备的振动一般都呈现出了强烈的非线性和背景噪声特性。而多年来仅使用单个传感器采集的局部振动信号去解决旋转机械系统故障辨识的努力,发展至今已呈现出了明显难以为继的困境。对此,应该充分利用布置在旋转机械若干关键截面处的系列传感器、依据尽量多的信息去实施智能故障决策技术,这种观点已获得了工业大数据技术研究展望的共识[2]。显然,传感器越多采集故障信息越丰富,但相应地故障特征数据集的维数就越高。因此,在实现旋转机械智能化运行维护管理的研究过程中,如何从非线性、强噪声、高维度的振动信号故障特征数据集合中,有效地提取出表征其运行状态的敏感量化特征,这对于发展大数据驱动的智能决策技术,具有非常重要的基础奠基作用和科学意义。
针对旋转机械振动信号的非线性、强噪声特性,如何利用振动信号辨识故障类别的问题,长期以来一直都在受到普遍地关注。其中,传统非平稳信号分析方法和小波分解方法因缺乏自适应性而不能获得有效的特征信息。经验模态分解(Empirical Mode Decomposition,EMD)是一种经典的时频分析方法,被广泛应用于特征提取问题的研究中[3-6]。但EMD缺乏完备的理论基础,具有端点效应、模态混叠、易受噪声影响、缺乏迭代终止标准等缺点。
2013年,法国学者Gilles[7]在小波变换的理论框架下结合经验模态分解的自适应性提出经验小波变换(Empirical Wavelet Transform,EWT)。EWT通过对信号频谱自适应划分构建正交小波滤波器,将单一信号分解为多个含有不同频率特征信息的模态分量,实现信号的降噪处理。该方法具有完备的理论基础,模态混叠少,较好的噪声鲁棒性等优点,已被应用于工程实践中[8-10]。
粗糙集理论[11-12]是一种对不精确、不完整、不一致数据集进行推理决策的智能数据分析工具,目前它在人工智能、数据挖掘、模式识别、故障诊断等领域已引起广泛关注。经典粗糙集只适用于离散符号型数据集的不确定性推理决策,在实际应用中,大量存在的连续属性值必须先进行离散化预处理,而离散化势必会导致不同程度决策信息丢失而影响分类效果[13]。邻域粗糙集(Neighborhood Rough Sets,NRS)[14]是利用邻域模型对经典粗糙集理论的拓展,主要是通过邻域对连续的论域空间进行粒化处理,以构成描述论域空间中任一概念的基本信息粒。由于NRS能处理连续属性值信息,而被广泛应用于故障诊断中[15-17]。在使用NRS时,一个关键问题是邻域半径的确定,Hu等为决策系统指定了唯一的邻域半径;文献[18]针对设置单一邻域半径对数据粒化处理时存在的缺陷,提出将属性值标准差引入到邻域半径的计算中,但并没有给出邻域半径的确定方法。文献[19]将概率统计的方法引入到NRS中,为解决邻域半径需要多次迭代调整问题提供了一种新思路,并在遥感影像分类中取得较好的效果。
鉴于经验小波变换在实现信号降噪处理时的优势,邻域粗糙集可有效处理连续属性值域的数据集,本文欲将EWT与加权多邻域粗糙集WMNRS(Weighted Multi Neighborhood Rough Set)结合对旋转机械故障特征提取方法进行研究,欲为海量故障数据集的工程应用提供理论参考依据。
1 相关原理简介
1.1 EWT的原理
EWT是在EMD基础上,将小波变换和窄带信号分析理论相结合提出的一种自适应信号处理方法。该方法的核心思想是根据待处理信号的频率特性对其频谱进行自适应分割,由此构建一组带宽适合的窄带带通滤波器,以提取具有紧支撑Fourier频谱特性的调频调幅模态。
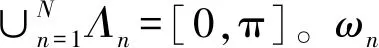
(1)
(2)
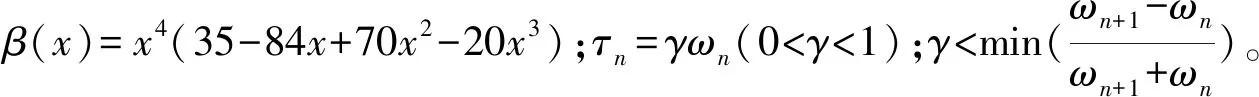
则EWT对信号f(t)分解的一般步骤可归纳为:
步骤1对f(t)进行FFT(Fast Fourier Transformation)变换,获得其傅里叶频谱F(ω)。
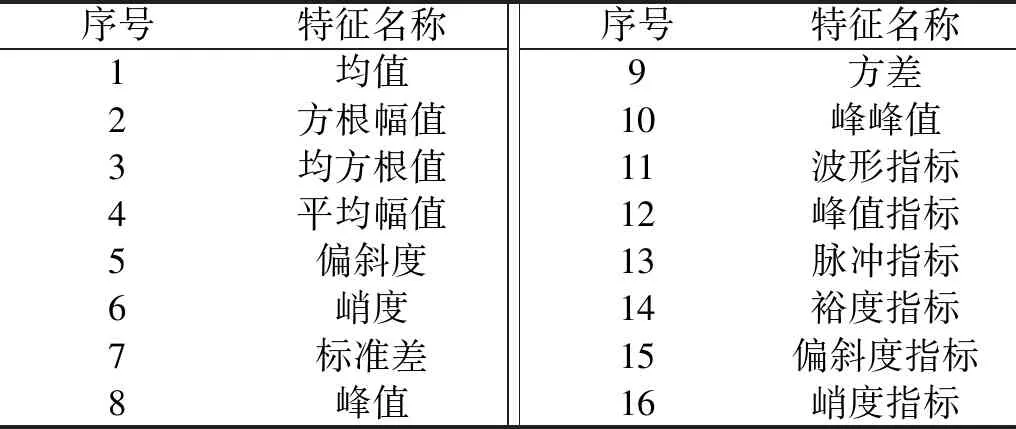
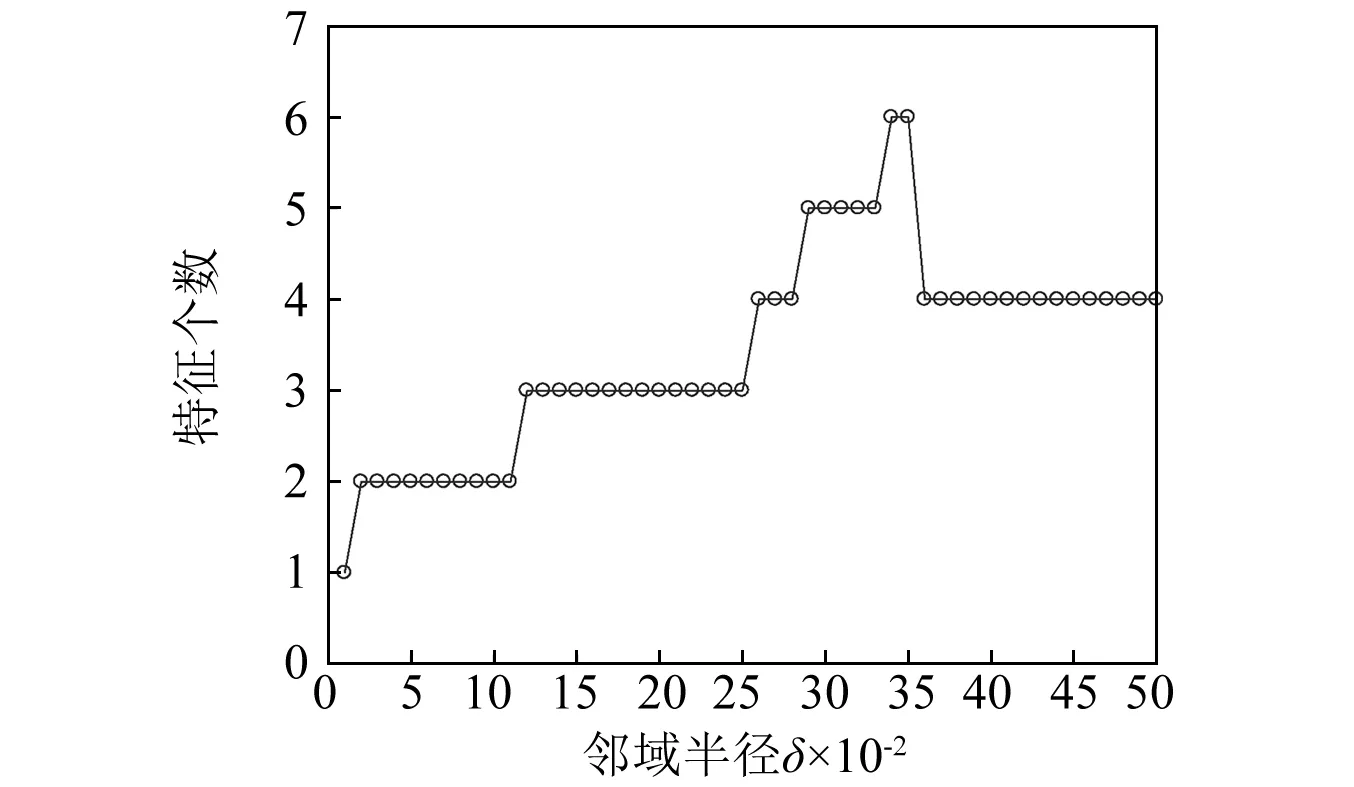
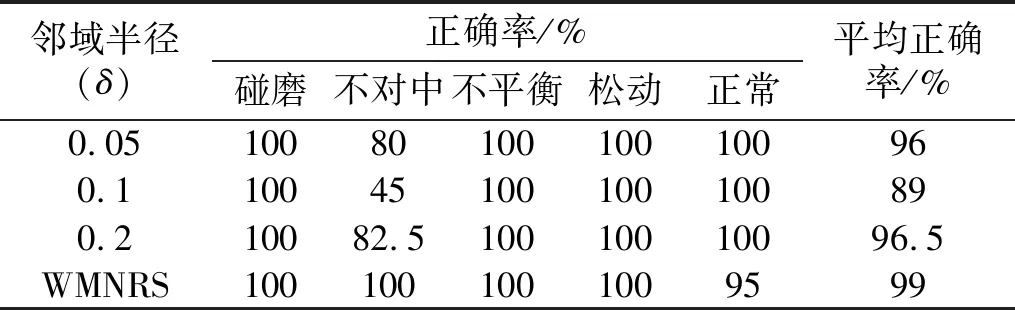
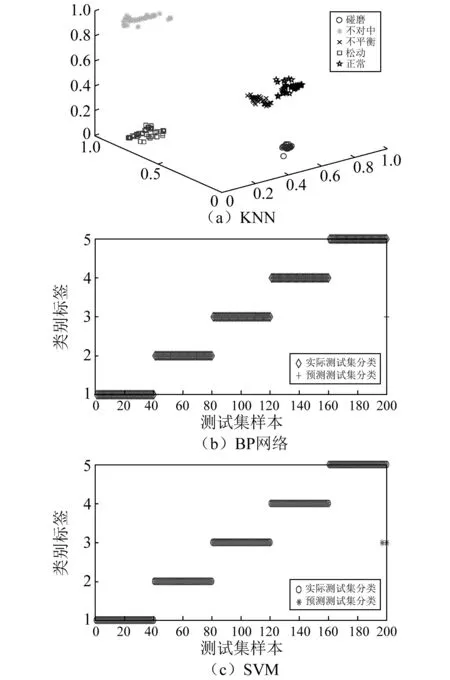
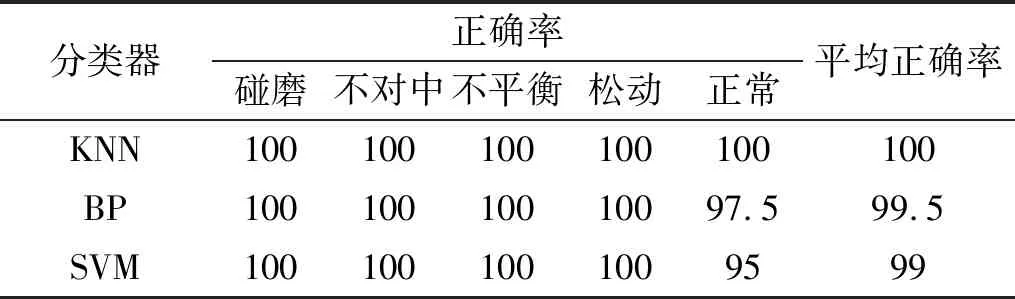
步骤2对F(ω)的频带范围[0,π]进行N个区间分割。区间分割的关键是N值的确定,一般来说可分为两种情况:①设f(t)由N个谐波分量组成,寻找|F(ω)|的M个极大值并降序排列。如果M≥N,则该算法找到足够的极大值,保留前N个极大值;②如果M (3) (4) 步骤4对信号进行重构,重构的结果为 (5) 步骤5根据式(5),信号f(t)可分解为 (6) 式中:*为卷积运算符号;cs(t)为分解得到的独立模式分量。 面对经典粗糙集理论仅适用于离散符号型数据集的不确定性推理决策状况,NRS追求的目标是期待能够解决好具有连续属性值域的数据集的分类与推理决策问题。它寄希望于通过有效的粒化处理手段,使具有连续属性值域的数据集能够呈现出一种粒状结构,以构成描述论域空间中任一概念的基本信息粒。关于邻域粗糙集处理连续属性值域数据集的一般方式基本如下。 给定一个由N个属性描述的数据集分类问题,可以将其形式化为一个决策信息系统S=〈U,A,D〉。论域U={x1,…,xn}为全部样本构成的集合,A={a1,…,aN}为描述样本属性集合,D为分类决策属性。当把属性张成一个空间,样本点就是空间中的点集。 定义1在给定实数空间Ω上,任一非空有限集合U={x1,…,xn},δ≥0,称点集δ(xi)={x|x∈U,Δ(x,xi)≤δ}为以xi为中心,以δ为半径的闭球,又称为xi的δ邻域。 定义2给定实数空间上的非空有限集合U={x1,…,xn},和U上的邻域关系NR,称二元组NAS=〈U,NR〉为一邻域近似空间。 定义1~定义3所包含的物理含义,可用图1所示的对一个连续空间实施二分类示意图表述。δ为邻域大小;⟡为第一类样本;□为第二类样本。对于样本x1来说,它的δ邻域内的所有样本都来自第一类,x1应该被划到第一类的下近似;同理,x3应该划到第二类的下近似。而对于样本x2来说,它的δ邻域内是两类样本的混合,应该划分到分类边界。在连续空间中,下近似包含的样本越多,分类边界包含的样本越少,样本的可分性就越高。 图1 连续空间的邻域关系Fig.1 Neighborhood relation of continuous space 定义5给定一个邻域决策系统〈U,NR,D〉,决策属性D对条件属性集B⊂C的依赖度定义为γB(D)=|NRB(D)|/|U| 定义6设a∈B,则属性a对B的重要度为:SIG(a,B,D)=γB(D)-γB-a(D)。 基于属性重要度的贪心式属性约简算法,应用广泛。该算法以空集为起点,计算每一个剩余属性的重要度,选择重要度最大的属性加入属性约简集合,直到全部剩余属性重要度小于设定的某一阈值,此时得到的就是最终属性约简集合。对于故障知识的发现,这种属性约简的结果将会更加有利于实际故障数据的分类运算。 本文所提出的经验小波变换与加权多邻域粗糙集结合的新故障特征提取方法,首先针对邻域粗糙集特征选择算法中邻域半径无法自动确定的问题,提出一种改进的加权多邻域粗糙集特征选择算法,实现了邻域粗糙集特征选择的自动化,然后将该算法与经验小波变化结合应用于旋转机械故障特征的提取。 由“1.2”节的定义4可知,样本xi的B邻域为所有与样本xi之间的距离小于指定邻域半径δB的样本集合。邻域半径δ的值选择的越大,意味着邻域集合包含的样本数就越多,邻域就越模糊,将导致样本无法区分,反之,邻域越清晰,样本可区分程度越高。如果邻域半径δ取值为0,则NRS就退化为经典粗糙集。因此,邻域半径δ的选取直接影响NRS特征约简的结果。加权多邻域粗糙集特征选择算法的基本思想是在邻域半径的取值范围[δmin,δmax]内,以步长Δδ分别对连续属性值域数据集进行多次特征属性约简,得到特征约简子集Aselc_i,然后统计数据集中的特征在多次特征约简中出现的概率,以概率作为权值与特征进行加权得到最终特征集,这样既能把区分度高的重要特征选出,又能剔除无效特征,以达到特征约简的目的。算法的具体步骤为: 步骤1设置邻域半径的取值范围[δmin,δmax],步长Δδ,则属性约简的次数K=(δmax-δmin)/Δδ+1。 步骤2初始化属性约简次数1≤i≤K。 步骤3调用邻域粗糙集属性约简算法计算邻域半径为δmin+(i-1)Δδ时的约简特征集Aselc_1,Aselc_2,…,Aselc_K。 步骤4统计特征aj出现的次数num(aj),其中aj∈Aselc_1∪Aselc_2∪Aselc_K,num(·)对象的个数,aj为编号为j的特征。 步骤5敏感特征集由特征加权得到Aselc={a1·ω1,a2·ω2,…}。 算法的具体流程如图2所示。 图2 WMNRS特征选择算法Fig.2 Feature selection algorithm of WMNRS EWT与WMNRS结合的故障特征提取方法,充分利用EWT的自适应性、抗噪能力强等特点,通过相关性分析选择EWT分解后的n个最优独立模式分量对信号进行重构,计算重构信号的时域特征指标作为量化特征,由于得到的量化特征集存在高维度及大量冗余问题,利用WMNRS特征选择算法自动选取维度低、敏感度高且分类错误率小的主要特征向量,最后通过多种分类器验证所提取特征的有效性。具体步骤如下: 步骤1对信号进行EWT分解,得到若干独立模式分量。 步骤2对分解的独立模式分量与原始信号进行相关性分析,选择相关性大的n个分量作为最优模式分量对信号进行重构。 步骤3计算重构后信号的时域统计指标作为量化特征向量,构建量化特征集。 步骤4利用加权多邻域粗糙集算法对量化特征集提取敏感主要特征。 步骤5在多种分类器上测试所提取特征的有效性。 数据处理的具体流程如图3所示。 图3 基于EWT与WMNRS的数据处理流程Fig.3 Data processing based on EWT and WMNRS 本文的实验对象是文献[20]中使用的一套双跨转子实验台。在该实验台的6个关键截面以相互垂直的方位安装12路电涡流传感器用于对转子系统振动信号的采集,在靠近电机端安装的13路传感器用于转子转速的脉冲计数。 在实验中模拟转子系统的动静碰摩、轴系不对中、转子不平衡、支承松动和正常五种运行状态。分别针对每种状态,在多次升降速下进行模拟实验并采集信号,这些振动信号真实地反映了转子系统的故障特征。在采样频率为5 000 Hz,转速3 000 r/min的条件下,以采样点数2 048点随机选取每种故障振动信号各80组,前40组作为训练样本,后40组作为测试样本。为了量化提取故障特征,采用的时域统计指标如表1所示。 表1 各通道振动信号选用的统计特征情况Tab.1 Statistical characteristics of the vibrationsignals in each channel 利用EWT对每一个通道的振动信号进行降噪分解,根据相关性分析[21]选择相关性大的4个模态分量对振动信号进行重构,计算重构信号的时域指标,则单通道的特征向量为16维,扩展至12个通道,即得高维故障特征向量12×16=192维。 邻域半径δ是邻域粗糙集的重要参数,它决定分类的粒度大小和分类边界区域训练样本的数量。不同的邻域半径,邻域粗糙集属性约简算法将得到不同的特征子集。到目前为止,邻域半径的确定没有统一的标准。参考Liu等研究中的处理方式,本文将有效的邻域半径设置为[0.01,0.5],步长为0.01,进行多邻域粗糙集属性约简实验,特征子集中属性个数与邻域半径之间的关系如图4所示。 图4 不同邻域特征子集的特征个数与邻域半径的关系Fig.4 Relationship between the number of characteristic subsets and neighborhood radius 在δ较小时,随着其值增大邻域粗糙集约简特征子集中特征个数增加,当达到最大值时,δ值再增加,特征子集中特征个数逐渐减少。即使特征个数相等的特征子集,其特征也并不都是完全相同的,比如δ=0.15,δ=0.2时特征子集中特征个数都是3,但是δ=0.15时特征子集中的特征为[48 124 3],δ=0.2时特征子集中的特征为[36 124 13]。因此,统计特征在多邻域粗糙集属性约简中出现的概率,对研究该特征表征转子系统运行状态的重要程度具有一定意义。 根据本文的实验方法,统计50次特征约简中各特征出现的概率如表2所示。 表2 EWT与多邻域粗糙集特征选择结果统计Tab.2 Statistics of feature selection results based on EWTand multi neighborhood rough sets 出现概率大于零的特征是对表征故障状态有用的特征,概率等于零的特征是冗余、不相关特征。转子系统振动信号经EWT降噪分解重构后,由时域统计特征指标构造的192维特征集,经过50次不同邻域半径的邻域粗糙集特征约简,共有26个特征出现概率大于零,剔除了166个冗余不相关特征,其中13号、124号特征出现概率最大为66%。为了计算简便,在既保证分类精度又体现特征重要性的前提下,本文选择概率较大的3个特征进行加权作为提取的加权特征向量。因此,本文对转子系统进行特征提取的结果为[0.66×a130.66×a1240.44×a94]。 为了验证加权多邻域粗糙集对故障特征提取的有效性,本文利用不同特征在分类器上的分类精度来衡量。将加权特征和所有特征分别输入PSO-SVM(Particle Swarm Optimization-Support Vector Machine)分类器进行对比实验。通过5×40组训练样本采用5折交叉验证的方法对SVM进行训练,选择RBF核函数,并使用PSO算法优化核函数参数σ和惩罚参数C以获得较高的分类准确率,最终的到训练好的SVM。将5×40组测试样本输入到训练好的SVM,测试其准确率。PSO优化时采用的粒子群种群规模为20,最大迭代次数为100,结果如图5所示。 图5 所有特征与加权特征的分类结果Fig.5 Classification results of complete feature sets and WMNRS 用所有特征进行分类时,不对中有10个测试样本被错分到支承松动,支承松动有1个测试样本被错分到正常;用加权特征进行分类时,只有2个支承松动的测试样本被错分到正常,在降低分类复杂度的同时,分类精度有一定的提升。加权特征与所有特征的分类正确率如表3所示。 表3 所有特征与加权特征的分类正确率Tab.3 Classification accuracy of complete featuresets and WMNRS % 为了验证“2”节所提方法的优越性,将加权特征和单邻域特征在分类器上进行对比实验。邻域粗糙集在使用的过程中,邻域半径δ一般选择某一确定值。当δ={0.05,0.1,0.2}时邻域粗糙集约简得到的单邻域特征子集分别为[24 13],[48 30],[36 124 30]。将单邻域特征与加权特征分别在Libsvm上用线性核(其它参数默认)支持向量机进行分类测试,结果如图6所示。 图6 不同δ下的SVM分类结果Fig.6 Classification results by SVM under different δ δ=0.05时,不对中有8个测试样本被错分成不平衡;δ=0.1时,不对中有22个测试样本分类错误,其中有3个被错分到支承松动,19个被错分到碰磨;δ=0.2时,不对中有7个测试样本被错分到支承松动;使用本文提出的WMNRS时,只有2个正常测试样本被错分到不平衡,具有比较明显的优势。不同邻域下的分类正确率如表4所示。 表4 不同δ下分类正确率Tab.4 Classification accuracy under differentδ 为验证本文所提方法提取特征的稳定有效性,分别采用KNN(K-Nearest Neighbor)、BP(Back Propagation)网络、SVM三种不同分类器[22-24]对“3.1”节中提取的转子系统敏感特征集进行测试,KNN的K值设置为1,BP网络隐含层神经元的个数设为10,测试结果如图7所示。 图7 不同分类器分类结果Fig.7 Classification results of different classifiers 从分类结果来看,测试集样本在三种不同分类器上测试都可以很“轻松”的使分类准确率达到99%以上,如表5所示。这充分说明特征提取的重要性,“优秀”的特征向量对模式识别具有决定性作用,同时也说明基于EWT与WMNRS的旋转机械特征提取方法稳定有效。 表5 不同分类器分类正确率Tab.5 Classification accuracy of different classifiers % 经验小波变换是近几年兴起的一种新信号自适应处理方法,具有理论基础完备,模态混叠少,噪声鲁棒性好的特点。加权多邻域粗糙集解决了邻域粗糙集邻域半径需要反复调整的问题。在此基础上,本文提出了一种新的故障特征提取方法,该方法将信号由经验小波分解降噪后重构信号的时域统计特征作为原始特征向量集,通过加权多邻域粗糙集提取故障信息的低维敏感特征,减少了冗余信息,简化了故障特征向量。本文通过实验,验证了基于EWT与WMNRS特征提取方法的有效性。同时,加权多邻域粗糙集增加了邻域粗糙集属性约简的计算量,下一步考虑如何提高运算效率的问题。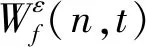
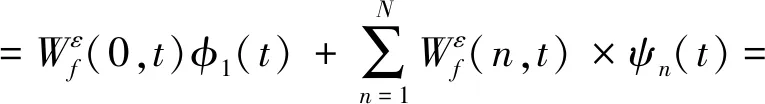
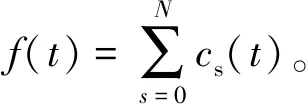
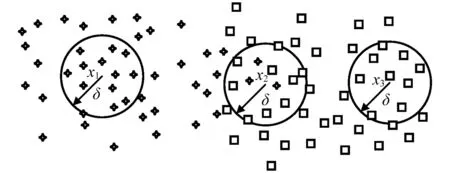
1.2 NRS的概念
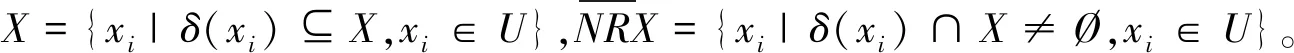
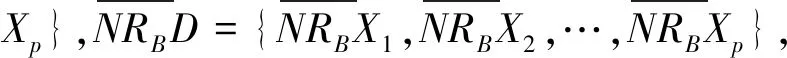
2 建立的故障特征提取方法体系
2.1 WMNRS特征选择算法
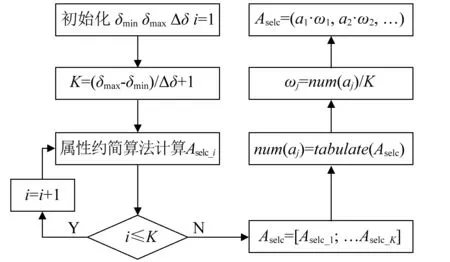
2.2 EWT与WMNRS结合的故障特征提取方法
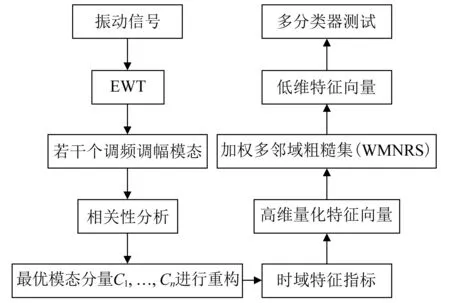
3 应用与分析
3.1 邻域半径对属性约简的影响
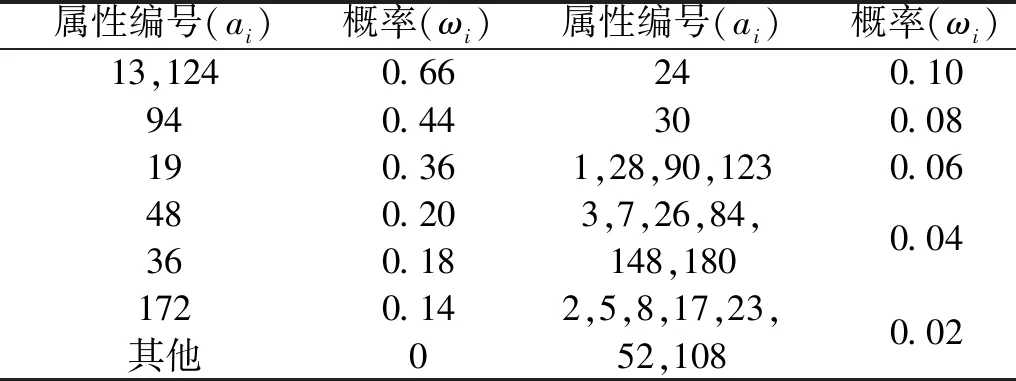
3.2 加权特征与所有特征对比分析
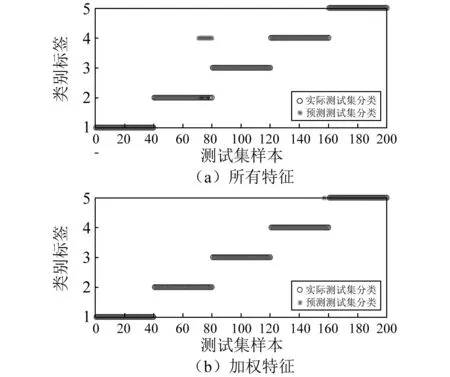
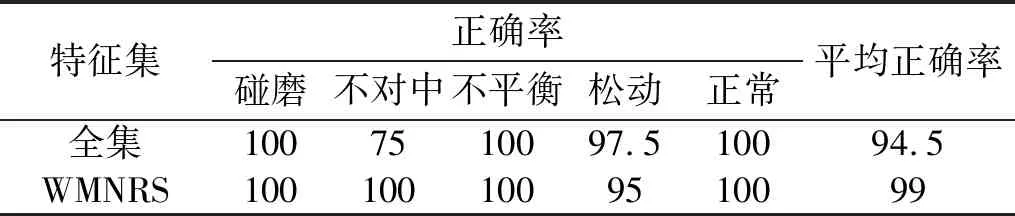
3.3 WMNRS与单一邻域粗糙集对比分析
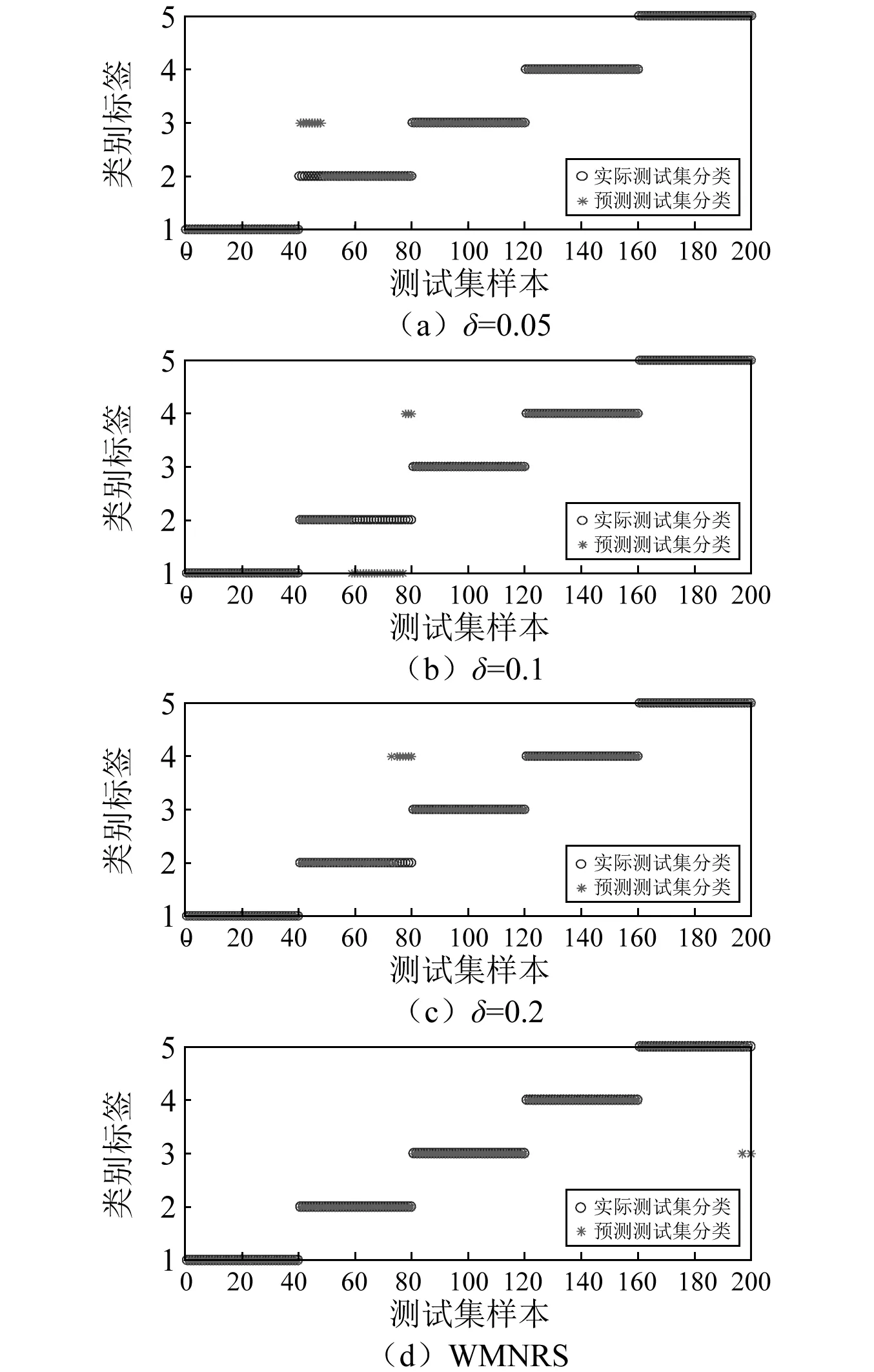
3.4 多分类器测试对比分析
4 结 论
