高铁简支梁桥横向地震碰撞效应振动台试验研究
2019-12-31孟栋梁杨孟刚
孟栋梁, 高 琼, 杨孟刚
(中南大学 土木工程学院,长沙 410075)
桥梁结构的横向抗震挡块常被用来限制地震作用下梁体的横向移位,防止横向落梁。大量公路桥梁震害资料表明,地震导致的横向碰撞震害是不可忽视的[1-2]。高铁桥梁的横向抗震挡块与公路桥梁有所不同:高铁桥梁抗震挡块为栓接于支座垫石内侧梁底的“工”字形钢挡块,横向碰撞为钢挡块与支座垫石之间的碰撞;而公路梁桥通常为盖梁处的混凝土挡块与梁体之间碰撞。汶川地震中,部分铁路桥梁同样出现了严重的横向位移震害[3],有必要针对铁路桥梁开展横向地震碰撞研究。
目前关于桥梁结构地震碰撞效应的研究主要集中在纵向碰撞和斜交桥的碰撞[4-6],大量有关于桥梁纵向碰撞的振动台试验也相继展开[7-11]。已有一些学者通过数值模拟的方法对桥梁结构横向地震碰撞效应展开了研究:Maleki[12-13]研究发现,挡块与梁体之间的碰撞本质上是非线性的,且碰撞效应受地震波的频谱特性影响显著,挡块与梁体之间的初始间隙是影响桥梁结构横向地震响应的一个非常重要的因素。Goel等[14]研究了桥梁结构的横向挡块在非一致地震激励下对梁体的限位作用,建议按线性挡块和不设挡块两种极限状态进行分析,计算结果可为非线性挡块情况提供上下界限。Bi等[15]建立了考虑桥梁横向碰撞的实体有限元模型,分析了碰撞对整个桥梁结构地震响应的影响,结果表明,在计算桥梁地震响应时,如果忽略挡块的碰撞效应可能会导致计算结果错误。文献[16-18]均以典型公路桥梁为例,研究了地震作用下挡块与梁体间的横向碰撞效应,并对影响横向碰撞效应的因素进行了参数分析。在高速铁路桥梁方面,石岩等[19]考察了高铁桥梁上部梁体与垫石之间的大偏心距碰撞对于桥梁结构横向地震碰撞效应的影响。杨孟刚等[20]基于ABAQUS建立了考虑轨道系统的横向地震碰撞实体有限元模型,对高铁简支桥梁横向地震碰撞效应进行了研究。
以往关于横向挡块的试验研究多集中于挡块的强度、破坏形式及耗能能力,鲜有涉及挡块与梁体间的碰撞对桥梁整体地震响应的影响:Bozorgzadeh等[21]通过对混凝土挡块的试验发现,混凝土挡块的典型破坏形式主要包括滑动剪切摩擦型、压-拉杆型、弯曲梁型;相似的研究也体现在文献[22-23]中。Li等[24-25]均研发了新型横向限位耗能装置,但该类型装置更类似于安装于桥墩和梁体之间的阻尼器,在地震作用下不会发生碰撞,与常见桥梁结构横向挡块的作用机理不同。
综上所述,虽然国内外学者对桥梁在地震作用下的碰撞响应已进行了大量研究,但主要是针对公路桥梁的纵向碰撞问题,对高铁桥梁的横向地震碰撞效应研究较少;以往关于桥梁结构的横向地震碰撞响应研究,主要是进行数值模拟和挡块本身的力学特性研究,尚无桥梁结构横向碰撞效应的振动台试验研究报道。本文以32 m标准跨径高铁简支梁桥为研究对象,按1∶6缩尺比设计并制作了单跨桥梁模型,通过振动台试验研究了地震波频谱特性、PGA(Peak Ground Acceleration)、挡块-垫石初始间隙等因素对横向地震碰撞效应的影响,并探讨了在挡块与垫石间填充橡胶缓冲垫层的防碰减震效果及橡胶垫层的减震机理。
1 试验模型及试验工况
1.1 试验模型设计
以1跨32 m标准跨径高速铁路双线简支梁桥为研究对象,上部梁体的重量为900 t,二期恒载取140 kN/m,上部结构的总重为1 356.48 t;桥墩为圆端形桥墩,墩高8 m;详细图纸资料参见通用图纸。挡块为高铁简支桥梁常见的“工”字形钢挡块,挡块参数如图1(a)所示,挡块-垫石初始间隙为3 cm;挡块的布置如图1(b)所示。试验在中南大学地震模拟振动台上进行,综合考虑振动台的尺寸及承载能力,试验模型的尺寸相似常数Cl取为1∶6,加速度相似常数为Ca=3。试验主要研究挡块与垫石之间的碰撞效应,因此挡块严格按照原型缩尺,弹性模量相似常数CE=1。通过量纲分析,可以确定其他相似关系,见表1。

表1 相似常数

图1 挡块的尺寸及布置Fig.1 Shear-key dimension and layout
需要说明的是:①在实际工程中,高铁简支梁桥一般为多跨连续布置,即每个桥墩相当于承担1片梁的质量,但取单跨桥梁进行试验时,每个桥墩只承受1片梁质量的1/2,因此为确保模型与实际多跨简支梁桥结构体系满足刚度及质量相似,在模型设计时取原型桥墩刚度的1/2,再进行缩尺;②试验前通过有限元仿真分析发现,在地震作用下桥墩基本处于弹性状态,桥墩非线性对各项地震响应影响可以忽略,为便于试验模型的制作及试验可重复性,桥墩材料选用钢材;③梁体在地震过程中相当于一个刚体,因此桥梁结构的跨度由于振动台尺寸限制未严格按照相似比缩尺,但上部梁体质量严格遵循相似关系。试验模型及测试装置的布置如图2所示。模型参数见表2。

表2 模型参数

图2 试验模型及测试装置Fig.2 Experimental model and test devices
桥梁原型支座为TJQZ6000球型钢支座[26],固定支座缩尺后的横向承载力为50.0 kN。为使支座力学参数严格按照相似比缩尺,本次振动台试验按照支座力学性能要求定制了一批支座,并通过试验测得固定支座的破坏荷载约为49.0 kN,满足缩尺要求;固定支座破坏后的力学性能同活动支座,活动支座的滑动摩擦力为4.0 kN。
挡块严格按照尺寸相似常数缩尺,材料采用与原型一致的Q235钢材,在顶板处开有两个“U”型孔,用于调整挡块-垫石初始间隙,挡块与梁底通过高强螺栓连接,并通过安装限位装置防止挡块在碰撞过程中产生滑动(见图2)。在试验前对挡块进行了单侧往复加载试验,试验加载面与碰撞接触面的尺寸相同,挡块的单侧往复加载曲线如图3(a)所示。其屈服荷载、破坏荷载分别为120.0 kN和220.6 kN,挡块的初始刚度为95.8 kN/mm。为探究橡胶缓冲垫层的防碰减震效果,在振动台试验开展之前对橡胶垫层进行了单侧往复加载试验,橡胶垫层的平面尺寸与碰撞接触面相同,橡胶的厚度与挡块-垫石初始间隙相同。橡胶垫层的单侧往复加载曲线,如图3(b)所示,橡胶垫层在试验程中展现出了良好的变形恢复能力及耗能能力,橡胶垫层的初始刚度为13.5 kN/mm。
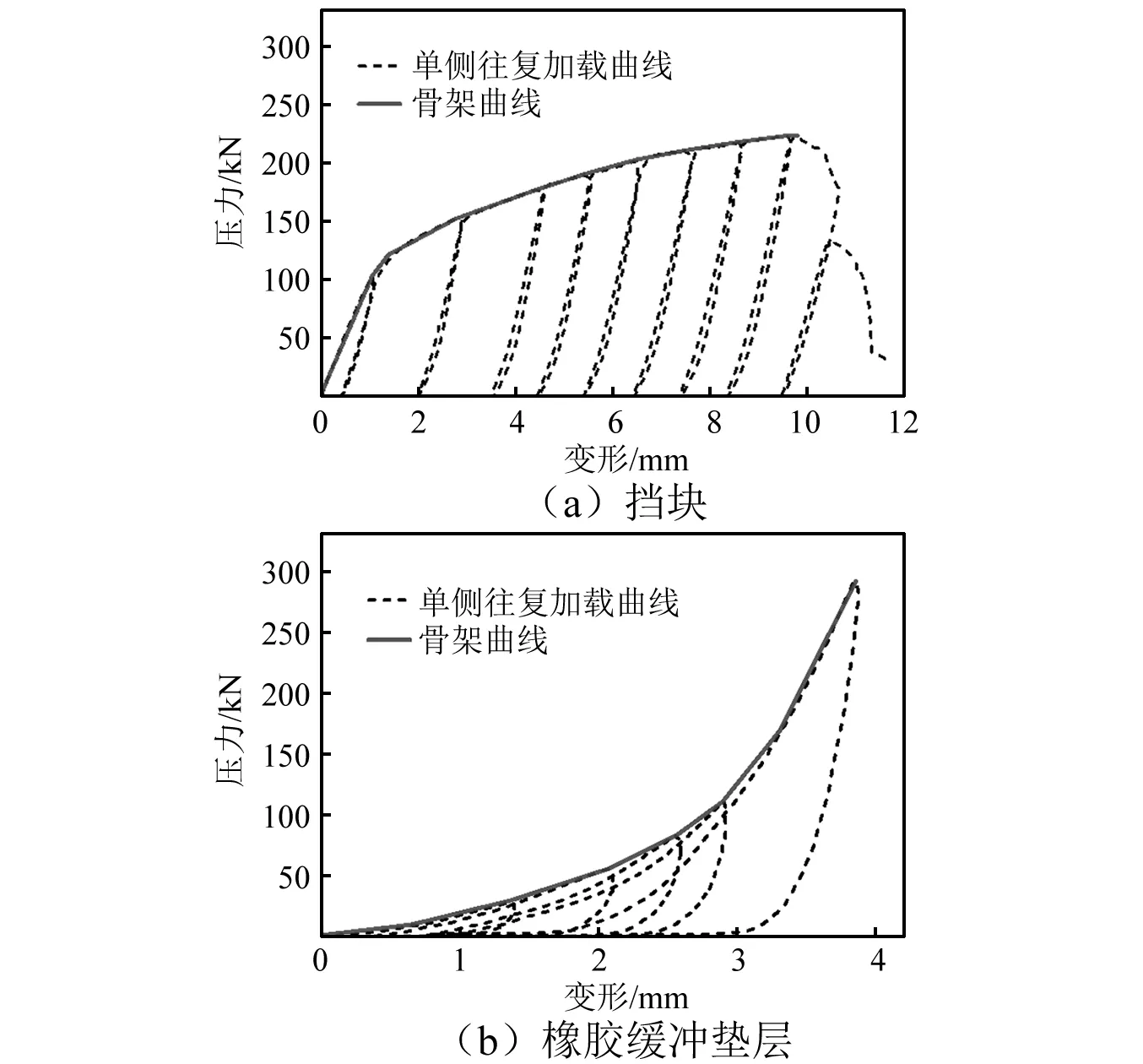
图3 挡块及橡胶缓冲垫层试验Fig.3 Tests of the shear key and the rubber bumper
所有支座、挡块及橡胶缓冲垫层在每一个试验工况完成后均进行更换。
试验测量的地震响应包括:墩顶位移和加速度、梁底位移和加速度、墩底弯矩以及碰撞力。其中,位移和加速度分别采用激光位移计和加速度传感器进行测量;墩底弯矩通过在桥墩底部布置应变片来测量。碰撞力的测试是一个重要环节,以往结构碰撞试验通常采用的是点-面接触的测力装置,其不能真实地模拟原型结构间面-面碰撞的接触形式。本次试验设计了一种可实现挡块与垫石间的面-面接触的测力装置(见图2),测力装置从垫石侧探出一块平面大小为110 mm×60 mm厚度为15 mm的钢板,钢板通过6根截面为15 mm×15 mm长度为30 mm的钢棒与垫石连接,利用钢板与挡块之间的面对面碰撞代替垫石与挡块间的碰撞,并沿每根钢棒纵向贴上金属应变片,通过采集测力元件钢棒应变时程换算得到挡块碰撞力时程。测力装置刚度刚度远大于挡块的刚度,且测力装置的屈服荷载大于挡块的破坏荷载(见表2),确保测力装置在试验过程中始终保持弹性状态。
1.2 试验工况
试验工况见表3。试验选取3条实测地震波(汶川波,Taft波和EL-Centro波)作为输入地震动,地震波的施加方式为一致激励。桥梁原型基于《铁路工程抗震设计规范:GB 50111—2006》8度设防,在多遇地震、设计地震及罕遇地震下的峰值加速度分别为0.07g,0.20g和0.38g。将选取的地震波首先分别调幅至0.07g,0.20g和0.38g,再按表1中加速度相似比(Ca=3)

表3 振动台试验工况

图4 罕遇地震激励下台面的实测地震波Fig.4 Measured ground motions on the shaking table under the excitations of high-level earthquakes
2 试验结果与讨论
2.1 试验现象
试验通过白噪声扫频识别结构的动力参数,并判定模型在经历一系列地震激励后桥墩是否出现损伤。试验测得模型的横向基频约为5.57 Hz,且随试验次数的增加,模型的横向自振基频基本不变。说明在试验过程中,模型基本处于弹性状态。通过半功率带宽法计算得模型的阻尼比约为3.15%。
图5为不同峰值加速度地震激励下固定支座的破坏情况。在多遇地震激励下,固定支座的限位挡板没有出现破坏,墩梁横向相对位移很小,未出现横向碰撞现象;在设计地震和罕遇地震作用下,横向固定支座的限位挡板出现屈服、剪断现象,墩梁横向相对位移增大,多数工况的挡块与垫石间发生碰撞。由于普通球型钢支座没有良好的复位能力,所以震后的残余位移具有一定的随机性,部分工况的震后残余位移较大,如图6所示。

图5 固定支座破坏情况Fig.5 Damages to fixed bearings

图6 震后残余位移Fig.6 Residual displacement after the test
挡块在试验中展现出了良好的限位能力,设置挡块后,墩梁间横向相对位移均明显减小,但由于挡块的强度较高,试验后挡块并未观察到明显的破坏或屈服变形。试验中,橡胶缓冲垫层的减震效果显著,且安装橡胶垫层之后,震后残余位移明显减小。试验前与试验后的橡胶缓冲垫层如图7所示。从图7可知,试验后橡胶垫层出现了明显的压痕和屈服变形。

图7 橡胶缓冲垫层的破坏情况Fig.7 Damage to the rubber bumper
2.2 地震波及PGA对横向碰撞效应的影响
将三种地震波调幅至多遇地震、设计地震、罕遇地震开展振动台试验。不同地震波及PGA对墩梁横向相对位移及碰撞力时程的影响如图8和图9所示。由图表分析可知:①多遇地震激励下,由于横向固定支座未发生破坏,支座能很好的约束上部梁体的位移,墩梁间横向相对位移较小,未发生横向碰撞;②在设计地震激励下,支座的横向限位挡板出现破坏(见图5(b)),墩梁相对位移明显增加。在汶川波、Taft波和EL-Centro波作用下的墩梁相对位移峰值分别为1.91 mm,5.60 mm和5.51 mm,其中Taft波和EL-Centro作用时,墩梁相对位移已经超过了挡块-垫石间的初始间隙,模型发生横向碰撞,碰撞力峰值分别为57.80 kN,53.91 kN。(3)在罕遇地震作用下,支座的限位挡板完全破坏(见图5(c)),墩梁相对位移进一步增大,挡块与垫石之间发生多次碰撞。在汶川波、Taft波和EL-Centro波激励下,墩梁横向相对位移峰值分别为5.88 mm,6.64 mm和6.43 mm,碰撞力峰值分别为95.01 kN,123.09 kN和116.82 kN。由以上分析可知,在多遇地震作用下,支座未发生破坏,上部梁体的限位作用仅由固定支座提供;在设计地震作用下,固定支座开始出现破坏,梁体的限位作用由固定支座和挡块共同提供;在罕遇地震作用下,固定支座完全破坏,梁体的限位作用主要由挡块提供。
在PGA相同的情况下,Taft波和EL-Centro波激励下桥梁横向地震碰撞响应大于汶川波激励下地震响应(见图8和图9)。可见,地震波的频谱特性对于桥梁结构的横向地震碰撞效应影响显著,在实际工程中进行挡块设计时,应结合具体场地条件加以分析。
各项地震响应峰值见表4。由表4可知,在罕遇地震作用下,挡块的最大碰撞力为123.09 kN,而挡块所能承受的破坏荷载为220.6kN(见表2),挡块仍有很大的强度富余。而美国AASHTO[27]中建议挡块的设计应在多遇地震中保持弹性,在设计地震水平下可以作为一种牺牲构件。由本文的试验结果可知,目前我国高铁简支梁桥横向抗震挡块的设计偏于安全,这有助于限制主梁的横向位移,但在极端地震作用下可能会加快桥墩的损伤进程。
图8 不同地震波及PGA对墩梁相对位移的影响Fig.8 Influence of different waves and PGA on the time histories of relative displacement between the pier and the girder

图9 不同地震波及PGA对碰撞力的影响Fig.9 Influence of different waves and PGA on the time histories of pounding force
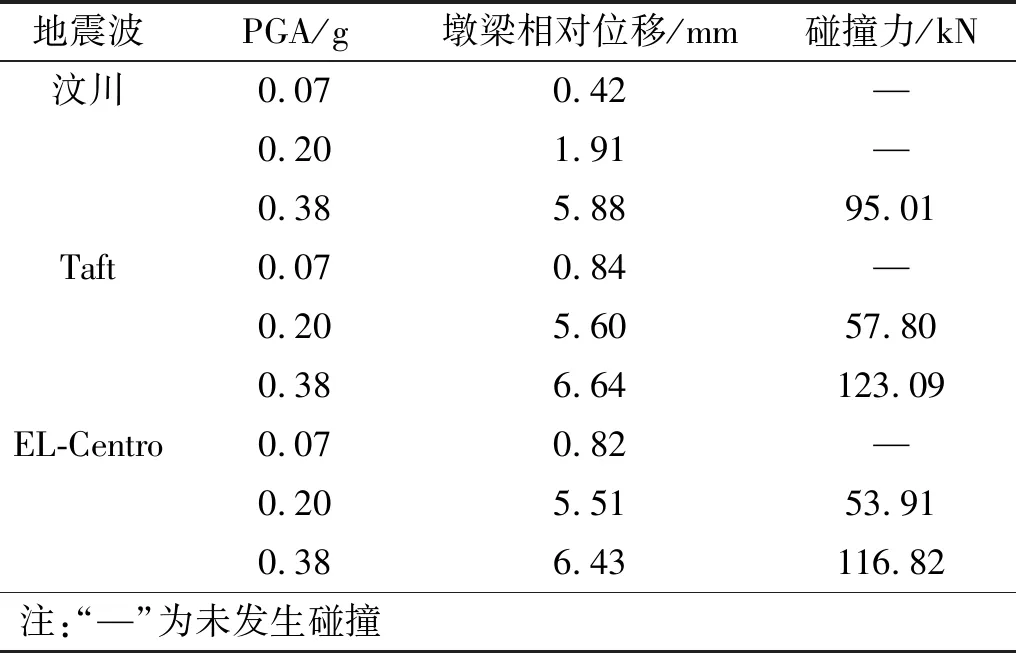
表4 不同地震波及PGA对地震响应峰值的影响
2.3 挡块-垫石间距对横向碰撞效应的影响
挡块-垫石间距是影响桥梁结构横向碰撞效应的一个重要因素,取挡块-垫石间距2.5 mm,5.0 mm,7.5 mm,10.0 mm及无挡块(对应于原型分别为1.5 cm,3 cm,4.5 cm,6.0 cm及无挡块)五种情形,输入0.38g的EL-Centro波,研究挡块-垫石间距对横向地震响应的影响。各项地震响应时程及地震响应峰值的变化分别如图10、图11所示。
挡块-垫石间距对墩梁相对位移时程的影响如图10(a)。由图10(a)可知,挡块在地震过程中展现出了良好的限位能力,在固定支座破坏后,挡块能将墩梁间的横向相对位移限制在一定的范围以内,无挡块时墩梁相对位移峰值为12.32 mm,当挡块-垫石间距为5.0 mm,墩梁相对位移峰值为6.43 mm,减幅为47.8%。墩梁相对位移峰值随挡块-垫石间距的增大而增大;挡块-垫石间距越小,挡块的限位效果越显著(见图11(a))。
图10(b)为挡块-垫石间距对碰撞力时程的影响。通过对比图10(a)可知,当墩梁横向相对位移超过挡块-垫石初始间隙时就会发生碰撞。由10(b)的局部放大图可知,碰撞不是在瞬间完成的,而是在某一微小时段内,挡块与垫石之间均存在相互作用,即碰撞有一定的持时[28]。Jankowski等关于桥梁结构纵向地震碰撞的研究结果表明,邻跨间距越大,碰撞力越大,减小邻跨间距,可以降低碰撞力,但会增加碰撞次数;而由图10(b)及图11(b)可知,随挡块-垫石间距的增加,碰撞力和碰撞的次数均呈现出减小的趋势。可见,桥梁结构的横向碰撞与纵向碰撞间存在很大的差异。
挡块-垫石间距对墩底弯矩时程的影响如图10(c)所示。通过对比图10(b)可以发现,在碰撞发生时,墩底弯矩会出现峰值,即碰撞会增大桥墩的地震响应。由图11(c)可知,随挡块-垫石间距的增大,墩底弯矩峰值呈下降趋势。实际上,可以认为不设挡块和挡块垫石间距为0为两种极限状态,当不设置挡块时墩梁相对位移最大,墩底弯矩最小;当挡块-垫石间距为0时墩底弯矩响应最大,墩梁相对位移最小。在进行抗震设计时,应综合考虑上部梁体及桥墩的地震需求选取合适的挡块-垫石间距。

图10 挡块-垫石间隙对地震响应时程的影响Fig.10 Influence of the initial gap on the time histories of seismic responses
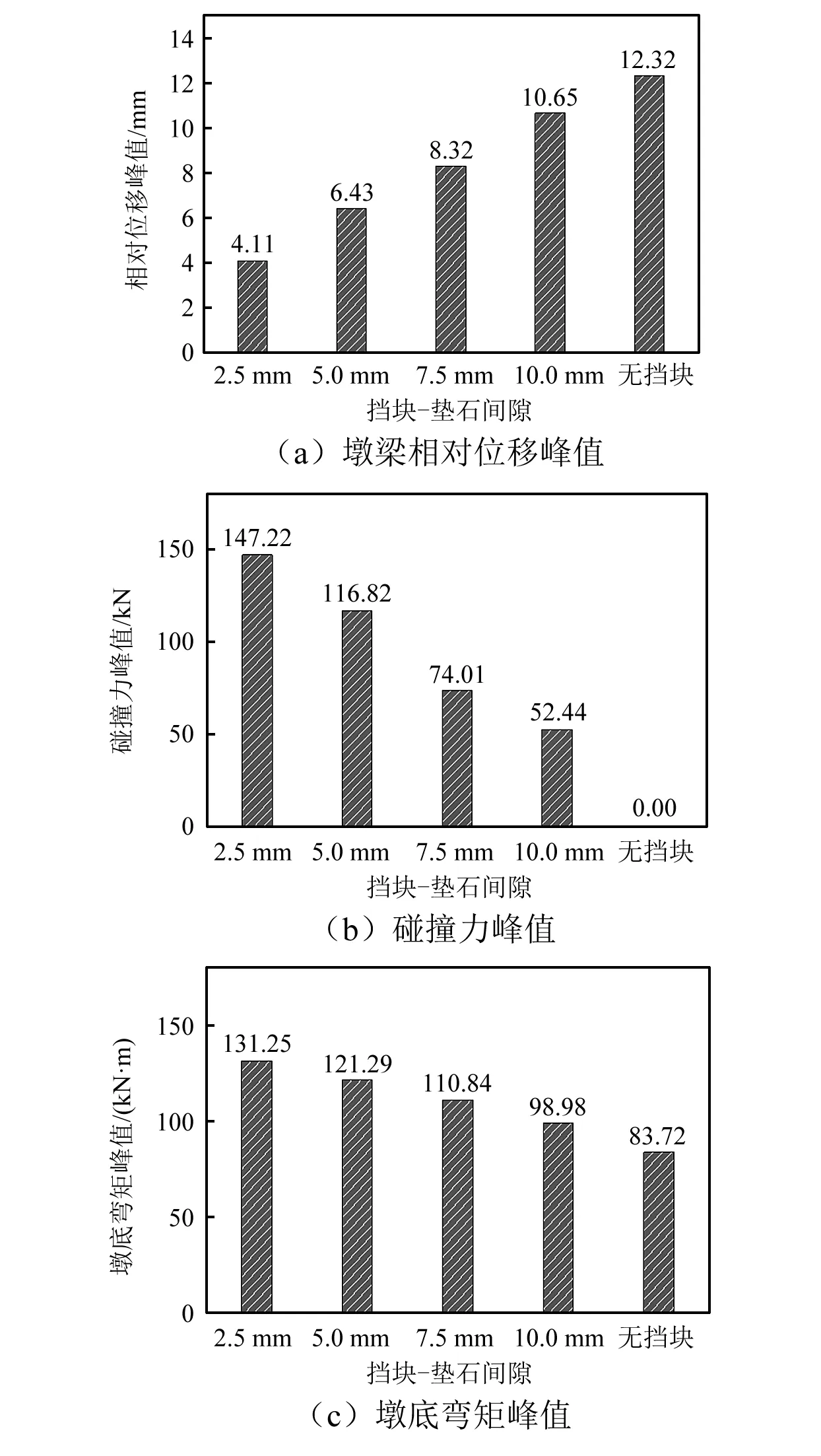
图11 挡块-垫石间距对地震响应峰值的影响Fig.11 Influence of the initial gap on peak seismic responses
2.4 橡胶缓冲垫层的防碰减震效果
由“2.3”节的分析可知,抗震挡块的设置能够限制上部梁体的横向位移的发展,但挡块与垫石间的碰撞会增大桥墩的墩底弯矩响应。考虑在挡块与垫石间填充满橡胶缓冲垫层,使挡块既能起到良好的限位作用,又能减小挡块碰撞带来的不利影响。为研究橡胶缓冲垫层的防碰减震效果,对无橡胶垫层和有橡胶垫层两种模型分别输入0.38g的汶川波、Taft波和EL-Centro波开展振动台试验。安装橡胶缓冲垫层后,墩梁相对位移、碰撞力及墩底弯矩时程的变化情况分别如图12、图13和图14所示。橡胶缓冲垫层对各项地震响应峰值的影响见表5。
2.4.1 墩梁相对位移
在挡块与垫石之间填充橡胶缓冲垫层之后,墩梁横向相对位移时程的变化如图12所示,峰值变化情况见表5。由图表可知,设置橡胶缓冲垫层之后,墩梁相对位移响应明显减小,其主要原因是设置橡胶缓冲垫层后,一方面,相当于减小了碰撞的初始间隙,使挡块更早地发挥限位作用;另一方面,橡胶缓冲垫层具有良好的耗能能力,加快了地震能量的耗散。由图12(b)和12(c)还可以发现,由于橡胶具有良好的变形恢复能力,在设置橡胶垫层之后,上部梁体的震后残余位移明显减小。
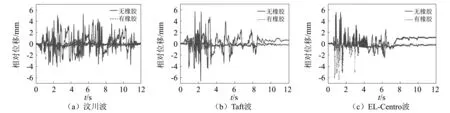
图12 橡胶缓冲垫层对墩梁相对位移的影响Fig.12 Influence of rubber bumpers on relative displacement between the pier and the girder

图13 橡胶缓冲垫层对碰撞力的影响Fig.13 Influence of rubber bumpers on pounding force

图14 橡胶缓冲垫层对墩底弯矩的影响Fig.14 Influence of rubber bumpers on bending moment at the bottom of the pier

表5 橡胶缓冲垫层对地震响应峰值的影响
2.4.2 碰撞力
橡胶缓冲垫层对于碰撞力时程的影响如图13所示。在设置橡胶垫层之后,挡块的碰撞力峰值显著减小,但碰撞次数明显增加。这主要是因为设置橡胶垫层之后,碰撞由挡块与垫石之间的碰撞变为橡胶垫层与垫石之间的碰撞,而橡胶垫层的刚度明显小于挡块的刚度,因此碰撞力会明显减小;但填充橡胶缓冲垫层后使得碰撞初始间隙减小为0,碰撞更容易发生,所以碰撞次数明显增加。由图13(a)可知,在汶川波激励下未设置橡胶垫层时,2#挡块并没有发生碰撞,而在设置橡胶垫层之后,碰撞间隙减小,使得2#挡块发生了碰撞。各挡块的碰撞力峰值变化,如表5所示。
2.4.3 墩底弯矩
橡胶缓冲垫层对于墩底弯矩时程的影响如图14所示,墩底弯矩峰值的变化情况见表5。由图表可知,在设置橡胶垫层之后,墩底弯矩响应有所减小,其主要原因是设置橡胶垫层之后,挡块与垫石之间的碰撞刚度减小,降低了地震碰撞所激起的高频响应,从而减小了墩底弯矩响应。
2.4.4 橡胶缓冲垫层的减震机理
为更深入的理解橡胶缓冲垫层的减震机理,以taft波激励下的墩底弯矩响应为例,对无挡块、仅设置挡块、同时设置挡块和橡胶垫层三种工况的墩底弯矩时程进行快速傅里叶变换,得到各种工况下的墩底弯矩响应的功率谱频率分布范围,如图15所示。由图15(a)可知,在无挡块时,墩底弯矩响应功率谱的主要频率分布范围为0~10 Hz,而模型的横向基频为5.57 Hz,可以认为在无挡块时墩底弯矩响应主要受结构的基频控制,因此定义该频率区间为基频区。而在设置挡块之后,挡块与垫石之间的碰撞使墩底弯矩响应的功率谱频率分布范围发生了明显的改变(见图15(b)),在基频区的功率谱幅值明显减小,而在10~20 Hz区间的功率谱幅值明显增大,说明碰撞激起了结构的高频响应,从而使得结构的地震响应发生改变。在设置橡胶缓冲垫层后,挡块与垫石之间的碰撞刚度减小,墩底弯矩响应功率谱的频率分布向基频区偏移,(见图15(c)),即橡胶垫层的设置减弱了结构碰撞时所引起的高频响应,从而减小地震作用下的墩底弯矩响应。由以上分析可知,碰撞会激起结构的高频响应,而橡胶的设置会减弱高频响应。
为解释上述现象,选取横向碰撞简化模型如图16所示。图16中,m1,kp,cp分别为桥墩转换至墩顶的质量、桥墩刚度、桥墩阻尼;m2,kb,cb分别为梁体质量、支座刚度、支座阻尼;将挡块与垫石间的碰撞简化为Kelvin模型[29],碰撞力为
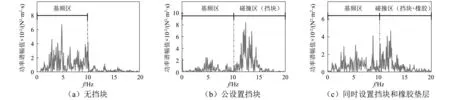
图15 墩底弯矩响应的快速傅里叶变换功率谱Fig.15 FFT of the bending moment at the bottom of the pier

(1)

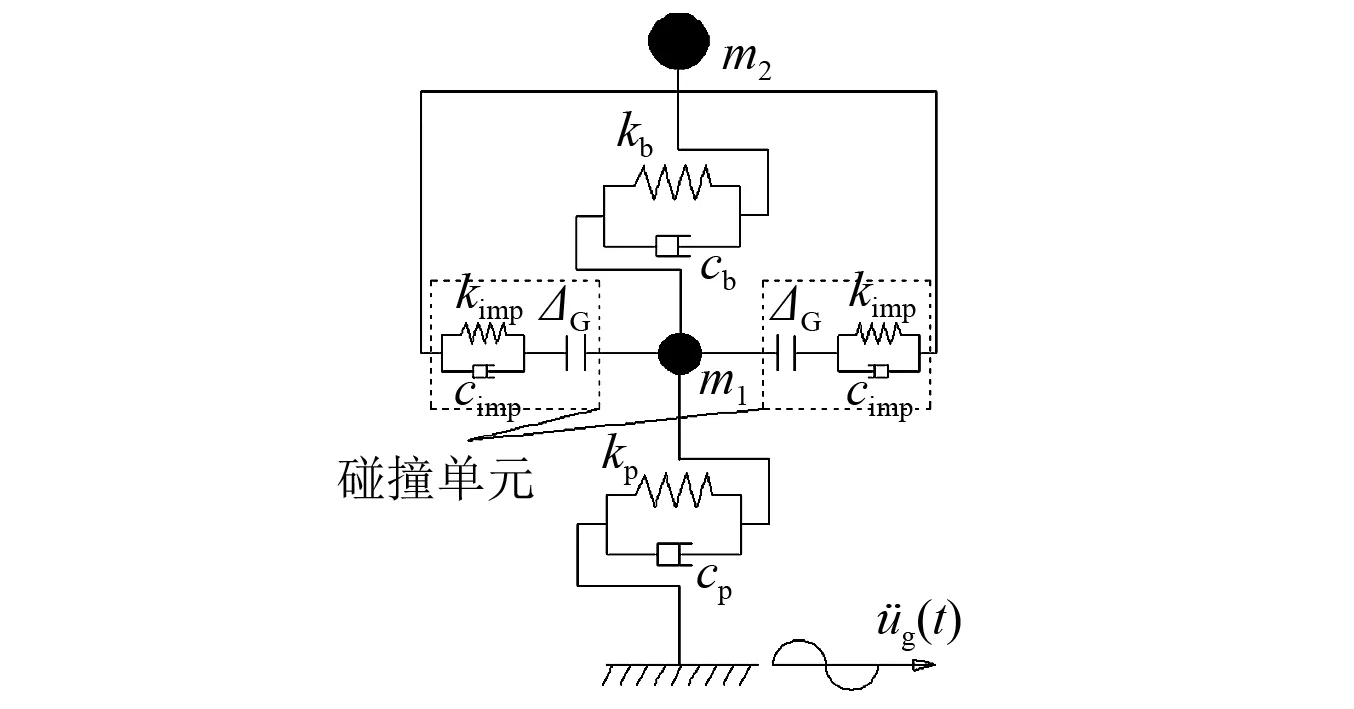
图16 横向碰撞简化模型Fig.16 Simplified model of transverse pounding
对于不设置挡块的情况,桥墩与上部梁体间的横向刚度(kp-g,1)仅由支座提供,即
kp-g,1=kb
(2)
对于只设置挡块的情况,当墩梁横向相对位移未超过ΔG时,挡块未起到限位作用,这时墩梁间的横向刚度与不设置挡块时相同;而当墩梁间的横向相对位移超过ΔG时,挡块可以看做与支座组成并联弹簧共同限制墩梁间的横向相对位移。为简单起见,kimp假定为挡块的初始刚度ks。桥墩与上部梁体间的横向刚度(kp-g,2)可以表达为
(3)
对于同时设置挡块和橡胶的情况,当橡胶缓冲垫层与垫石之间发生碰撞时,碰撞单元的刚度可以被等效为橡胶垫层(kr)与挡块(ks)组成的串联弹簧的刚度,即kimp=(kskr)/(ks+kr)。则桥墩与上部梁体间的横向刚度(kp-g,3)可以表达为
(4)
对比式(2)~式(4)可知,对于无挡块的情况(无碰撞),只由支座提供对上部梁体的约束作用,结构的横向刚度及自振频率较小。对于仅设置挡块的情况,当挡块与垫石之间处于碰撞接触状态时,结构的横向刚度及自振频率明显增大,而台面实测地震波的功率谱(见图4)主要分布在较高的频率范围,因此会导致结构地震响应的高频成分明显增大(见图15(b))。对于同时设置挡块和橡胶垫层的情况,碰撞刚度由于橡胶的设置而明显减小,当结构处于碰撞接触状态时,结构的横向刚度和自振频率相较于仅设置挡块的情况有所减弱,从而减少结构地震响应的高频成分(见图15(c)),达到减震的效果。
3 结 论
以1跨32 m标准跨径高速铁路简支梁桥为研究对象,按1∶6缩尺比设计并制作了横向碰撞振动台试验模型,开展了17个工况的振动台试验。试验主要研究了地震波的频谱特性及PGA,挡块-垫石间距对桥梁结构横向碰撞效应的影响,并探讨了橡胶缓冲垫层的防碰减震效果。主要结论如下:
(1)试验再现了桥梁结构在地震作用下的横向碰撞过程。在多遇地震作用下,支座未出现破坏,挡块与垫石之间无碰撞发生,上部梁体的横向约束作用仅由支座提供;在设计地震激励下,支座开始出现破坏,多数工况发生了碰撞,上部梁体的约束作用由支座和挡块共同提供;在罕遇地震激励下,支座完全破坏,模型均发生了碰撞,上部梁体的约束作用主要由挡块提供。
(2)挡块的横向限位效果显著,但挡块与垫石之间的碰撞会增大结构的自振频率,从而激起结构的高频响应,增大桥墩的墩底弯矩响应;随挡块-垫石初始间隙的减小,墩梁横向相对位移峰值减小,碰撞力峰值及墩底弯矩峰值增大;在进行挡块设计时,应综合考虑上部梁体及桥墩的地震需求选取合适的挡块-垫石初始间隙。
(3)橡胶缓冲垫层具有良好的防碰减震效果,在挡块与垫石之间填充橡胶缓冲垫层后,一方面相当于减小了挡块与垫石间的初始间隙,使得挡块的横向限位效果更加显著,以0.38g的EL-Centro波激励为例,设置橡胶缓冲垫层后墩梁相对位移峰值减幅为77%;另一方面,橡胶缓冲垫层的设置降低了挡块与垫石之间的碰撞刚度,减小了碰撞力及碰撞所引起的结构高频响应,从而达到减震的效果,在0.38g的Taft波激励下,碰撞力和墩底弯矩最大值分别减小64%,15%。
