基于双维度变化的形态学多重分形的战场声目标识别

张 坤， 邸 忆,2， 顾晓辉

(1.南京理工大学 机械工程学院，南京 210094； 2.武昌理工学院 信息工程学院，武汉 430223)

坦克与直升机是现代地面战争中主要的突击力量，近年来，采用声目标探测识别技术对其进行识别被广泛应用[1]。对战场声目标的特征提取是声目标识别技术中的关键步骤，具有良好区分度的特征有助于简化分类器的设计，提高目标识别率。同时两者的声信号表现出非平稳、非线性、短时、强噪声的特点增加了特征提取的难度，所以对战场声目标的特征提取的研究具有重要意义。

传统的识别方法是针对信号的时域与频域进行特征提取来进行识别[2]。为表征信号的非线性行为，可采用分形维数进行描述[3-6]。文献[7]就采用分形维数对战场声目标进行了特征提取的研究，说明了该方法的可行性。但在实际应用中单一的分形维数只能从整体来反映信号的不规则性，而多重分形维数可以精确的体现信号的局部奇异性[8]。计算多重分形维数的方法一般运用盒计数法，该方法采用了规则的网格划分，这会造成一定的计算误差，且计算量较大[9]。文献[10]提出了一种基于数学形态学计算多重分形维数的方法，该方法无需网格划分，运用形态学的结构元素进行覆盖，具有精度较高，便于实现等优点，因此在齿轮运动状态的识别中取得了良好的效果。然而将上述方法应用于战场声目标识别时发现，不同类目标声信号的分形维数特征区分度不明显，目标识别精度较低。

为了能够快速提取的声目标的有效特征参量，本文在已有的形态学多重分形维数计算方法的基础上提出了一种基于双维度变化的数学形态学多重分形计算方法。为达到改变原有计算方法得到的分形维数偏小的问题，使尺度在时间与幅值上均发生改变，重新定义了配分函数，同时引入回归分析对分形尺度与本文所提的分配函数进行拟合，保证了两点法求斜率作为分形特征的准确性，再以运算速度与识别率为标准，筛选出最优的两个尺度直接计算多重分形维数。半实物仿真试验验证了本文所提方法得到的多重分形维数结果更符合分形理论的要求，且计算效率较已有算法有了明显提升，同时将本文算法和文献[10]算法运用于战场声目标的特征提取与识别，在相同条件下，本文算法提取的特征具有更高的识别率。

1 多重分形维数

信号的多重分形是用谱函数来描述信号的不同层次的分形特征，计算多重分形谱的过程较复杂，一般采用配分函数法进行定义[11]。在尺度ε下，沿时间轴将信号划分为单位长为ε的信号段，第i段信号的幅值之和为si(ε)，所有幅值之和为∑si(ε)，得第i段信号的配分函数为

(1)

假设信号被分为N段，在尺度ε下，由广义维数方法得到谱函数的表达式为

(2)

多重分形维数定义为

(3)

当q=0时为容量维数

(4)

当q=1时为信息维数

(5)

当q=2时为关联维数

(6)

由此可见，多重分形维数涉及了分形理论大部分分形维数。它的引入在一定程度上弥补了单重分形维数只能从单一测度描述信号的缺点，使信号的分形特征得到了拓展，能从多个测度对信号进行描述，为分形学应用于时间序列的信号处理提供了理论基础[12-13]。同时多重分形维数计算主要涉及加减运算，乘除运算很少，为实现信号的快速处理提供了一种极佳选择。

2 双维度变化的数学形态学的多重分形

数学形态学方法的基本思想是用一定形态的结构元素去度量信号。在保证信号基本形态不变的前提下，用结构元素覆盖信号，从而去除信号中的细节得到简化的数据，使用的结构元尺度越小，得到信号细节的就越丰富。分形维数的估计方法也是在不同尺度下对信号进行的一种度量，因此数学形态学就提供了一种极佳的求解分形维数的方法[14]。但一般基于数学形态学计算多重维数，尺度仅在信号幅值域变化，当信号长度较大时，会导致计算的配分函数差异不明显，未能达到尺度变化后，度量也发生变化的要求，求出的多重分形维数也就无法反映信号的非线性特征。本文提出在时间域与幅值双维度尺度进行变化，就可以解决该问题，更好的反映出信号的非线性特征。

2.1 数学形态学覆盖

数学形态学的基本运算包括腐蚀与膨胀。设f(n)和g(m)分别定义在F={0,1,2,…,N-1}和G{0,1,2,…,M-1}上的离散函数，且N≫M。f(n)为输入信号，g(m)为结构元素。

则f(n)关于g(m)的腐蚀定义为

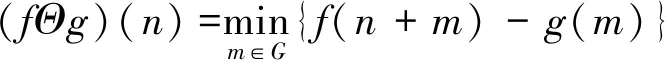
(7)

则f(n)关于g(m)的膨胀定义为

(8)

腐蚀与膨胀运算具有信号滤波的作用，一般腐蚀运算减小了信号的峰值，填补了信号的谷底；膨胀运算扩大了峰顶，增大了信号谷值。采用这两种运算可构筑信号的轮廓线，从而完整覆盖信号，为分形维数的计算提供基础[15]。

假设离散信号f(n)，n=1,2,…,N，单元结构元素定义为g，在尺度ε下所用结构元素定义为

(9)

则信号在尺度ε下的形态覆盖面积Ag(ε)为

(10)

2.2 双维度变化的形态学分形维数计算方法

对信号完成形态学覆盖后，根据多重分形的定义，关键在于分配函数的计算方法。文献[10]提出的配分函数Pi(ε)定义为

(11)

式中：f⊕εg(n)-fΘεg(n)相当于对f(n)的离散值进行覆盖，作用如同单个网格上的盒子数。根据式(2)与式(3),利用最小二乘法拟合数据点(lnε,Kq(ε))，其斜率即为多重分形维数Dq(ε)。该种方法在计算每个尺度下的分配函数时，项数与信号数据量相同，信号数据量较大时，Pi(ε)会很小，且随尺度的变化不够明显，这会造成计算出的分形维数失真。

本文提出的改进方法主要是配分函数的算法与文献[10]的不同。借鉴盒计数法的思想，在对信号进行形态学覆盖后，每次计算配分函数的项数也应随尺度的变化而变化，即在时间维度与幅值维度均进行变化。膨胀与腐蚀运算完成对幅值域的变化，根据尺度确定配分函数个数即对时间域的变化。这两种变化同步进行，相较原方法中仅有信号幅值发生尺度变化，每次的变化程度更大。随着尺度越大，对信号的描述就越粗略，配分函数的项数就越少。相对于原方法配分函数个数不变，得出分形维数精度更高。定义的基于双维度变化的配分函数(Double Dimensions Changed Distributed Function, DDCDF)为

(12)

则谱函数变为

(13)

即计算的“盒子”不仅在幅值上随尺度变化，在时间轴上也随着尺度变化，改变了文献[10]方法中尺度仅沿幅值变化的状况。但尺度选择上应满足N/ε为正整数的关系。采用该种算法可将文献[10]算法中较多的乘除运算改为加法运算，大大减少了运算量，也更符合分形中尺度变化的思想。同时解决了当信号长度较大时，计算的分形维数不能够反映出信号非线性的问题。计算出分配函数Pi(ε)与谱函数Kq(ε)后，就可由式(3)得到多重分形维数Dq。

在利用式(3)计算多重分形维数时，多采用最小二乘法拟合，然后计算拟合直线的斜率，作为多重分形维数Dq的结果。本文通过对数据进行线性回归证明与相关性检验说明谱函数Kq(ε)与尺度lnε满足极好的线性关系，为选取其中两点直接计算(lnε,Kq(ε))的斜率奠定了数据与理论基础。再以运算速度与目标识别率为标准，筛选了最优的两个尺度作为拟合直线的两点，直接计算斜率作为多重分形维数。

3 试验分析与比较

为说明本文方法的可行性与有效性，进行了半实物的仿真试验。图1所示为原理图，四个相同的声传感器S1，S2，S3，S4均匀布置在半径为25 cm的圆盘平台上，声源距圆盘圆心处距离为333 cm。

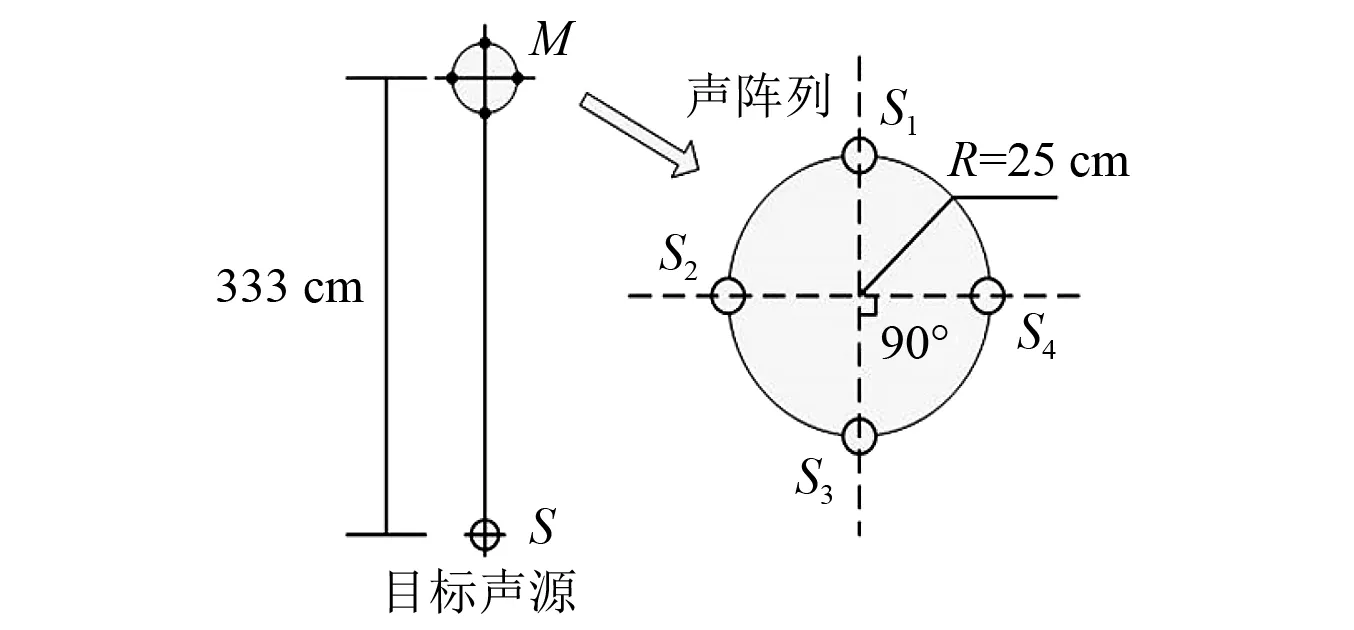
图1 声信号采集原理示意图Fig.1 Schematic diagram of acoustic collection

声源及装置均保持静止。采用PXI数据采样系统对声信号进行采集，采样频率为20 kHz，量程-4～+4 V。实物图如图2所示。

图2 声信号采集装置实物图Fig.2 Acoustic collected platform

利用该装置采集坦克与直升机声目标，测量信号的长度均为1 024个采样点，信号在处理前经过了调理电路进行了滤波预处理，所得的坦克与直升机的声信号与频谱如图3所示。

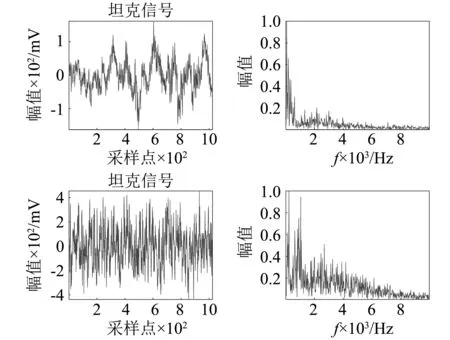
图3 声信号时域与频域图Fig.3 Acoustic signals and frequency spectrum

通过两种声音的频谱图可知，坦克与直升机声的主要能量集中约在0～3 000 Hz，同时直升机声较坦克声有着更多高频分量，这在时域图上的表现是振动的幅度和频率较大，这也为利用多重分形对两种信号进行特征提取提供了基础。

以一组坦克声信号为例，说明改进的数学形态学多重分形维数计算方法。运用数学形态学方法估计分形维数时，关键在于单位结构单元的选取与尺度的选择。为减小运算量且提高覆盖信号的质量，结构元素选择扁平结构g={0,0,0}，在尺度选择上，需要进行线性拟合，为减小计算量，尺度采用离散化取值，最大的取值不超过信号长度的一半，但所取值须能被信号长度整除，以保证计算的精度。由于信号样本长度均为1 024，为满足N/ε为正整数，则尺度ε∈[2,4,8,16,32,64,128,256,512]。对信号进行形态学覆盖，图4为选取尺度为8与16的结构元素对一组典型的坦克声与直升机声信号进行了形态学覆盖。

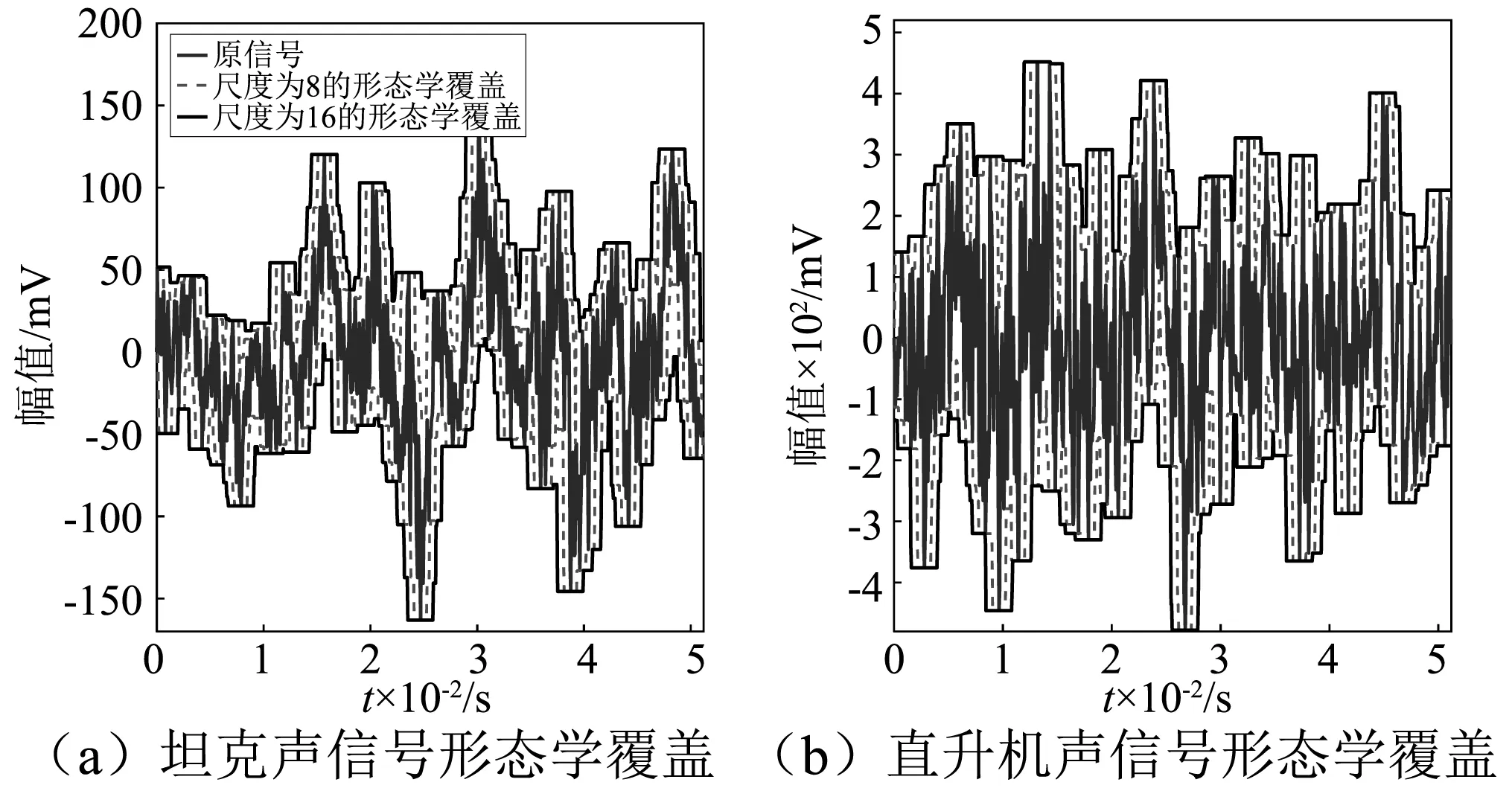
图4 两种声信号形态学覆盖图Fig.4 Morphological cover of the two kinds of signals

对信号进行形态学覆盖后，根据式(12)与式(13)计算配分函数Pi(ε)与谱函数Kq(ε)，q=2,3,…,10，表示为谱函数中的指数。为证明Kq(ε)与lnε的线性关系首先需要对回归方程的显著性进行检验[16]，再进行相关分析说明两个变量的相关程度。引入回归系数β，检验统计量Fq(ε)，将(lnε,Kq(ε))经最小二乘法拟合得

(14)

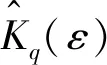
(15)

根据统计学原理，假设：β=0则

Fq～Fα(1,n-2)

(16)

式中：α为显著性水平，一般令α=0.01，因为样本点(lnε,Kq(ε))个数为9则得临界值为

F0.99(1,7)=12.2

(17)

若Fq≥F0.99(1,7)，则可认为线性回归效果显著。通过回归检验，需对两个变量进行相关检验，引入总体相关系数γq与样本相关系数rq分别表示当谱函数指数中q为时的相应统计量，满足式(18)

(18)

rq的计算公式与γq相同，由于样本相关系数rq是总体相关系数γq的一致估计量，能否真实表现变量总体的相关情况受到随机因素于样本总量的影响，故需对其检验。总体相关系数的检验统计上用t检验。

假设：τq=0则

(19)

当总体相关系数为0时，统计量t1服从t分布。一般设显著性水平α=0.01，因为样本点(lnε,Kq(ε))个数为9则

tα/2(9-2)=3.499

(20)

若tq>tα/2(7)则认为rq通过了显著性检验，可认为lnε与Kq(ε)满足线性关系。

选取坦克与直升机声信号各60组，分别计算了这120组声信号的Fq值与tq值，发现均满足Fq≥F0.99(1,7)与tq>tα/2(7)，且远远大于条件值，说明(lnε,Kq(ε))满足良好的线性关系。随机选取其中5组声信号的Fq与tq，如表1和表2所示。

以表1以及表2中的声信号1为例，当q=2,3,…,10时，统计量最小为F10=3 617.86，t10=60.15均远大于条件值F0.99(1,7)与tα/2(7)，说明通过声信号1计算得到的(lnε,Kq(ε))满足线性关系，使用两点直接计算斜率仍能保证很高的拟合精度。同样地，其他声信号的Fq和tq计算结果均表现出了较高的拟合精度，故可选择其中的两点来计算这120组声信号的改进的多重分形维数。

表1 5组声信号的Fq值

表2 5组声信号的tq值

由此分析可知：ε∈[2,4,8,16,32,64,128,256,512]，则一共应有36种组合。为筛选出最优的尺度组合，以计算所得多重分形维数为特征输入，利用支持向量机进行两种声目标的识别，选取60组声信号作为训练集，另外60组作为测试集，分别比较这36个组合的识别率与计算速度，根据需要选择识别率高，运算速度相对较快的一组。其识别率以及运算速度(指计算10组信号多重分形维数的时间)，如图5所示。

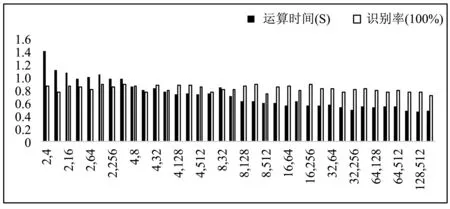
图5 不同尺度组合下的运算时间与识别率Fig.5 The computing times and recognized rates of the different scale groups

由图5选取运算时间在0.6 s以下，而识别率在85%以上的为最优组合，其中当ε=[16,256]时为最优解。此时用时为0.57 s，识别率为90%。选取坦克与直升机声信号各10组采用本文提出的改进快速算法，选择尺度为ε=[16,256]，计算这20组声信号的多重分形维数，并与文献[10]的方法进行比较，提取的多重分形维数谱图如图6、图7所示。

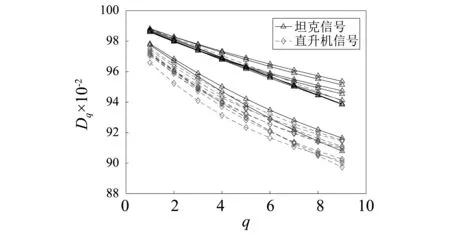
图6 本文方法(DDCDF)提取的多重分形维数Fig.6 Multifractal dimension calculated by DDCDF

由图6可知，坦克声信号的多重分形维数基本大于直升机的多重分形维数，但中间仍有少许混杂。采用文献[10]的方法得出两者的多重分形维数混杂较为严重，且求出的值较小均为负值，而本文提出的算法计算的多重维数基本在[0.8,1]，更利于后续的目标识别。本文方法较文献[10]最大优势在于运算速度的提高。为了适应计算机的运算，文献[10]算法中选择的尺度为ε=[2,4,8,16,32,64,128,256]，需要进行8次形态覆盖，又因为信号长度为1 024，计算配分函数需要1 024次除法，则计算一组信号的维数就需要次除法运算。本文方法选择了ε=[16,256]，只需两次形态学覆盖，同时计算分配函数时需要2 048次加法运算和69次除法运算，则文献[10]方法计算复杂度为O(4m×n)，本文方法为O(m×n)，计算120组声信号的多重分形维数，本文方法用时5.16 s,而文献[10]的算法需用时21.41 s,在运算效率上有了明显提升。

图7 文献[10]提取的多重分形维数Fig.7 Multifractal dimension proposed by article [10]

为比较本文算法与文献[10]算法提取的特征用于战场声目标识别的差异，选取直升机与坦克声信号各120组，分别用本文方法与文献[10]的方法提取的多重分形维数作为声音识别的特征，采用支持向量机进行识别，其识别结果如表3所示。

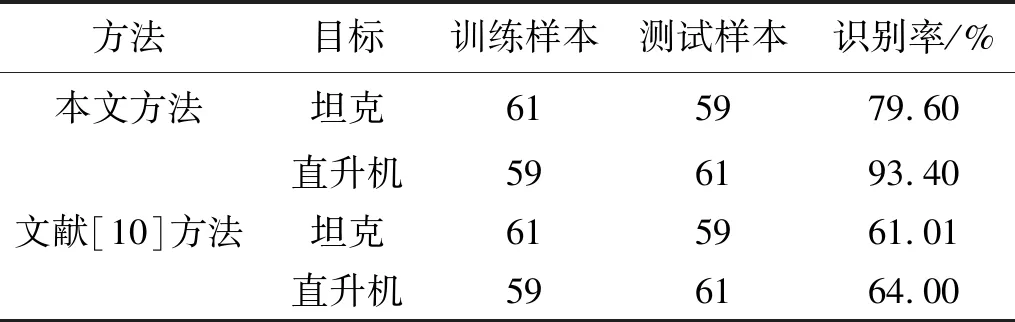
表3 两种方法识别结果比较

由表可见采用本文方法在两类目标识别上均要远远优于文献[10]的方法，且直升机声的识别率达到了93.4%。通过以上比较可知，本文提出的改进方法在战场声目标识别方面从运算速率与识别精度上均要优于文献[10]提出的方法，总识别率高了23.5%。

4 结 论

(1)本文提出了一种基于双维度变化的形态学多重分形计算方法，并运用于战场声目标识别。为减少运算量使结果更精确，重新定义了配分函数，使时间与幅值两个维度都可进行改变，相较之前仅在幅值域上改变，更符合分形维数计算的理论要求。

(2)分形维数实质为(lnε,Kq(ε))拟合直线的斜率，本文使用线性回归的理论证明了拟合直线的精度很高，可由两点直接计算斜率而保证精度。再以运算速度与识别率为标准，筛选出最优的两个尺度直接计算多重分形维数。减少了形态学覆盖的次数，进一步减少了运算量。

(3)在半实物仿真实验中，运用本文提出的改进算法与文献[10]提出的形态学分形计算方法在计算速度与声目标识别率上进行了对比，结果表明，本文方法计算复杂度为O(m×n)，文献[10]方法计算复杂度O(4m×n)，而识别率上比文献[10]的方法高了23.5%。该种算法主要涉及加减运算，也适用于硬件实现，为战场声目标识别的应用提供了一种更为有效的方法。