颗粒冲击形式对阻尼器能量损耗影响的研究

2019-12-31宋晓宇尹忠俊

振动与冲击 2019年24期

宋晓宇，尹忠俊，陈兵

(北京科技大学机械工程学院，北京 100083)

生活中，人们常用“一盘散沙”来形容一些涣散的、无组织的系统或者群体。但对于受振颗粒体系，颗粒之间的运动并不是互不相关的，而是通过颗粒间的摩擦与碰撞表现出整体性或协同性。颗粒阻尼器就是利用颗粒与颗粒以及颗粒与腔壁之间的非弹性碰撞和摩擦消耗系统的能量，从而达到减振的目的[1-2]。

由于颗粒阻尼复杂的非线性耗能机理，关于颗粒的研究主要以实验与数值仿真为主要手段。Yang[3]设计了多项试验，细致研究了激振频率、振幅、颗粒填充率、尺寸等因素对颗粒阻尼有效质量和损耗功率的影响规律。Wong等[4]采用离散元的方法，在充分考虑颗粒的质量和转动惯量的前提下，使用弹簧、阻尼以及滑动摩擦界面来建立模型，并测量恢复力系数以及界面摩擦因数来预测其能量损耗，具有较高的精度和计算效率。毛宽民等[5-6]从颗粒微观力学角度研究了非阻塞性微颗粒阻尼(Non-Otstructive Particle Damping,NOPD)的作用机理，并对颗粒与主结构之间的能量传递及该过程中的能量损耗进行了定量的分析，发现NOPD的摩擦耗能量与冲击耗能量具有相同的量级。姚冰等[7-8]对颗粒的减振机理以及在直升机叶片上的应用[9]等多方面进行了深入研究并取得了一些有意义的成果。胡溧等[10-11]对颗粒阻尼的动态特性以及影响颗粒阻尼的内外因素进行了比较系统的研究。

近年来，颗粒阻尼在建筑领域也越来越被重视。鲁正等[12-13]将调谐质量阻尼器与颗粒阻尼器相结合，扩大了减振频带，增加了减振的鲁棒性，并将其引入高层建筑风振控制领域，通过风洞试验以及近似的数值模拟方法对这种新型阻尼形式的阻尼特性进行了深入的研究。赵玲等[14]以空心柱为研究对象，通过自由振动试验系统研究了颗粒参数(颗粒材料、填充率、质量比等)和结构参数的变化对结构减振效果的影响。

然而，目前对颗粒阻尼的研究主要集中在外界激励和颗粒本身参数对阻尼效果的影响，关于颗粒对系统冲击方式造成的能量耗散差异的研究仍没有深入展开。振动颗粒间存在着非弹性碰撞和摩擦，导致颗粒体系能迅速耗散掉颗粒自身及外界输入的动能，这也使得颗粒的运动具有整体性，体现为颗粒对容器底部的冲击力呈现窄脉冲式[15]。在不同的振动强度下，颗粒对系统的冲击力会表现出冲击分岔现象[16-17]。

随着计算机性能的提升以及离散单元法[18]的完善，该方法已经成为研究颗粒运动的重要方法。基于离散单元法的EDEM仿真可以跟踪区域内每个颗粒的受力状态与速度矢量，极大地突破了实验中由于测量手段单一所带来的局限性。

为探究冲击形式与损耗功率之间的依赖关系。本文采用离散单元法对圆柱形和圆台形两类容器(共6种)的颗粒阻尼器进行了不同工况的研究。首先将圆柱Ⅰ与圆台Ⅳ进行对比复现颗粒间的相互作用过程，通过分析冲击形式解释产生能耗差异的微观本质。然后研究腔壁倾角的渐变过程，得出腔壁倾角、冲击形式以及能量耗损之间的相互关系。

1 仿真模型及参数

1.1 离散单元法

接触模型是离散单元理论的核心。本文的仿真实验均采用软颗粒接触模型，该模型中将颗粒单元的接触过程进行法向和切向分解，其法向接触力方程为

(1)

颗粒单元的切向运动可分解为切向滑动与颗粒单元的滚动

(2)

(3)

式中：mij为颗粒单元i，j的等效质量；Iij而为颗粒单元的等效转动惯量；s为旋转半径；un，us分别为颗粒单元的法向和切向相对位移；θ为颗粒单元自身的旋转角；Fnij，Fsij分别为颗粒单元所受外力的方向和切向分量；Mij为颗粒所受外力矩；cn，cs分别为接触模型中的法向和切向阻尼系数；Kn，Ks分别为接触模型中法向及切向刚度系数。

由Hertz[19]接触理论颗粒之间与作用力之间的关系为

(4)

(5)

(6)

式中：a为接触圆半径；α为法向叠合量；q0为最大接触压力；F为颗粒之间的总压力；Ri和Rj分别为两接触颗粒的半径；ki，kj分别为颗粒的压力分布比例尺。

(7)

(8)

式中：vi，vj分别为两接触颗粒的泊松比；Ei，Ej为两接触颗粒的弹性模量。则法向刚度系数表达式为

(9)

根据Mindlin切向接触力求解方法[20]，得到切线刚度计算公式

(10)

式中：Gi，Gj分别为两颗粒单元的剪切模量。

由牛顿第二定律，可以得到颗粒的运动方程为

(11)

利用中心差分法[21]对式(11)进行数值积分，得到以两次迭代步长的中间点的更新速度为

(12)

式中： Δt为时间步长。

对式(12)进行积分处理，则可以得到位移等式

(13)

进行再次积分则可以得到位移更新表达式

(14)

由此，可以得到新的位移，然后带入力-位移关系式运用牛顿第二定律计算新的作用力，实现跟踪每个颗粒在任意时刻的运动。

1.2 仿真模型

本文建立的3D NOPD颗粒系统仿真模型，如图1所示。包括圆柱形容器和圆台形容器两类(共6种)。

图1 DEM颗粒阻尼仿真模型Fig.1 DEM model of the NOPD

所有容器的高H均为40 mm，下端面直径D2为14.2 mm(除圆柱Ⅱ外)，容器形状参数见表1。文中涉及的所有颗粒阻尼器除形状外，其它参数设置(包括材质参数、颗粒参数等)均严格一致。其中圆柱Ⅰ的模型及材料等参数都是基于姜泽辉等研究中所用实验材料而设定，相关参数设置如表2所示。在仿真过程中阻尼器受到竖直向上的正弦激励，保持振动频率f=60 Hz不变，振动强度Γ分别为2.63，3.83，8.06，8.75，9.64，11.72，12.61，14.56，15.72，具体选取原则见姜泽辉等的研究。

表1 DEM仿真容器形状参数

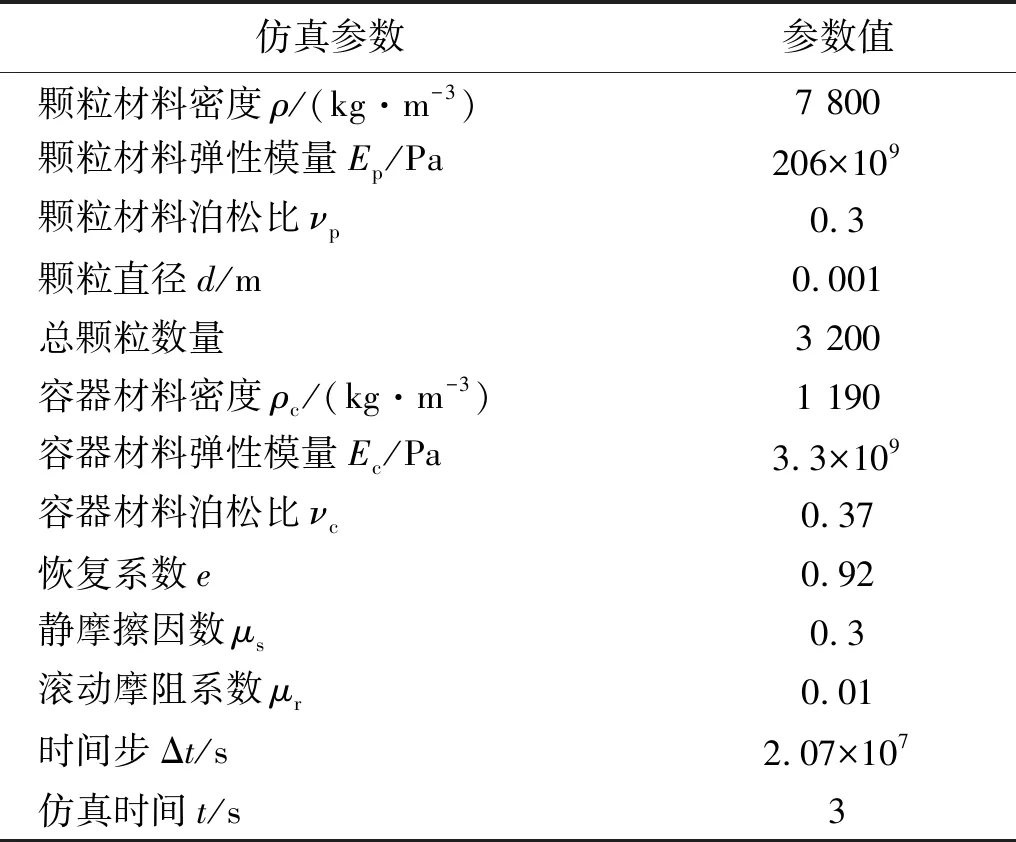
表2 DEM仿真材料特性及参数

2 结果与讨论

2.1 模型验证以及冲击形式的比较

通过分析圆柱Ⅰ内颗粒对系统的冲击结果(见图2)发现，在Γ=9.64和Γ=14.56时，冲击信号内分别存在20 Hz和15 Hz的谐波，说明在Γ=9.64和Γ=14.56时容器内颗粒产生周期分岔现象(分别为三倍周期分岔和四倍周期分岔)。而在Γ=2.63时并没有谐波的出现，所以此时颗粒并没有产生分岔。以上结果与姜泽辉等所得的结论一致。通过图3也发现仿真结果与姜泽辉等研究中(文献中图1)的实验结果基本一致，所以本文中仿真模型以及相关参数设定比较可靠。

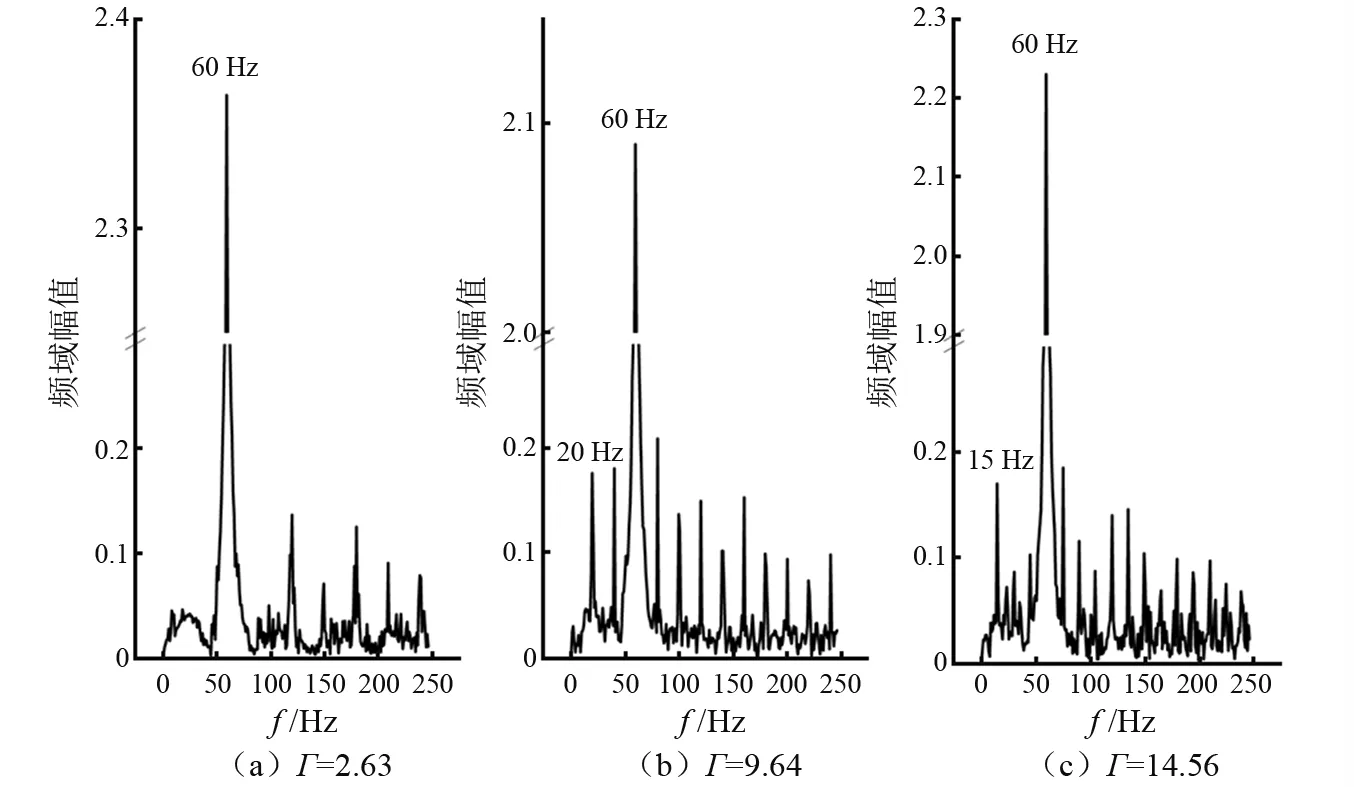
图2 圆柱Ⅰ内颗粒对系统冲击力信号的FFT频谱图Fig.2 FFT spectrogram of particle-to-system impact in cylinder Ⅰ

为了突出对比结果，本文首先将倾角最大的圆台Ⅳ与圆柱Ⅰ进行对比。仿真结果显示，在振动强度以及其它参数一定的条件下，两种容器内的颗粒对系统呈现出截然不同的冲击方式(见图4)。在振动强度较低时(Γ=2.63,Γ=3.83)，颗粒对两种容器的冲击次数以及冲击力度基本相同。但是随着振动强度的提高，圆柱Ⅰ内的颗粒出现了非常规律的周期分岔现象(表现为冲击脉冲稀疏)，而圆台Ⅳ内颗粒对系统的冲击次数要远远多于圆柱形。也就是，随着振动强度的提高，圆台Ⅳ对冲击力的分岔现象表现出明显的抑制作用。

由图4可知，当Γ=14.56时，在0.2 s内圆台Ⅳ内颗粒对系统的平均冲击力为2.04 N，冲击次数为8次；圆柱Ⅰ内颗粒对系统的平均冲击力为4.2 N，冲击次数为4次。在该强度下，圆台形容器内颗粒每次对系统的平均冲击力仅为圆柱形的51%，但冲击次数几乎是其二倍。所以本文中将圆台Ⅳ内颗粒对系统的这种冲击形式称为“小而密”型，圆柱Ⅰ内颗粒对系统的冲击形式称为“大而疏”型。研究发现造成二者冲击形式不同的原因主要与容器内颗粒的运动形式有关。

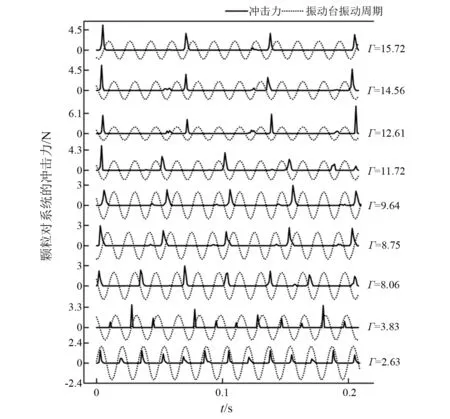
图3 圆柱Ⅰ内颗粒对系统的冲击力随时间的变化Fig.3 The impact force of particles-to-system in cylinder Ⅰover time

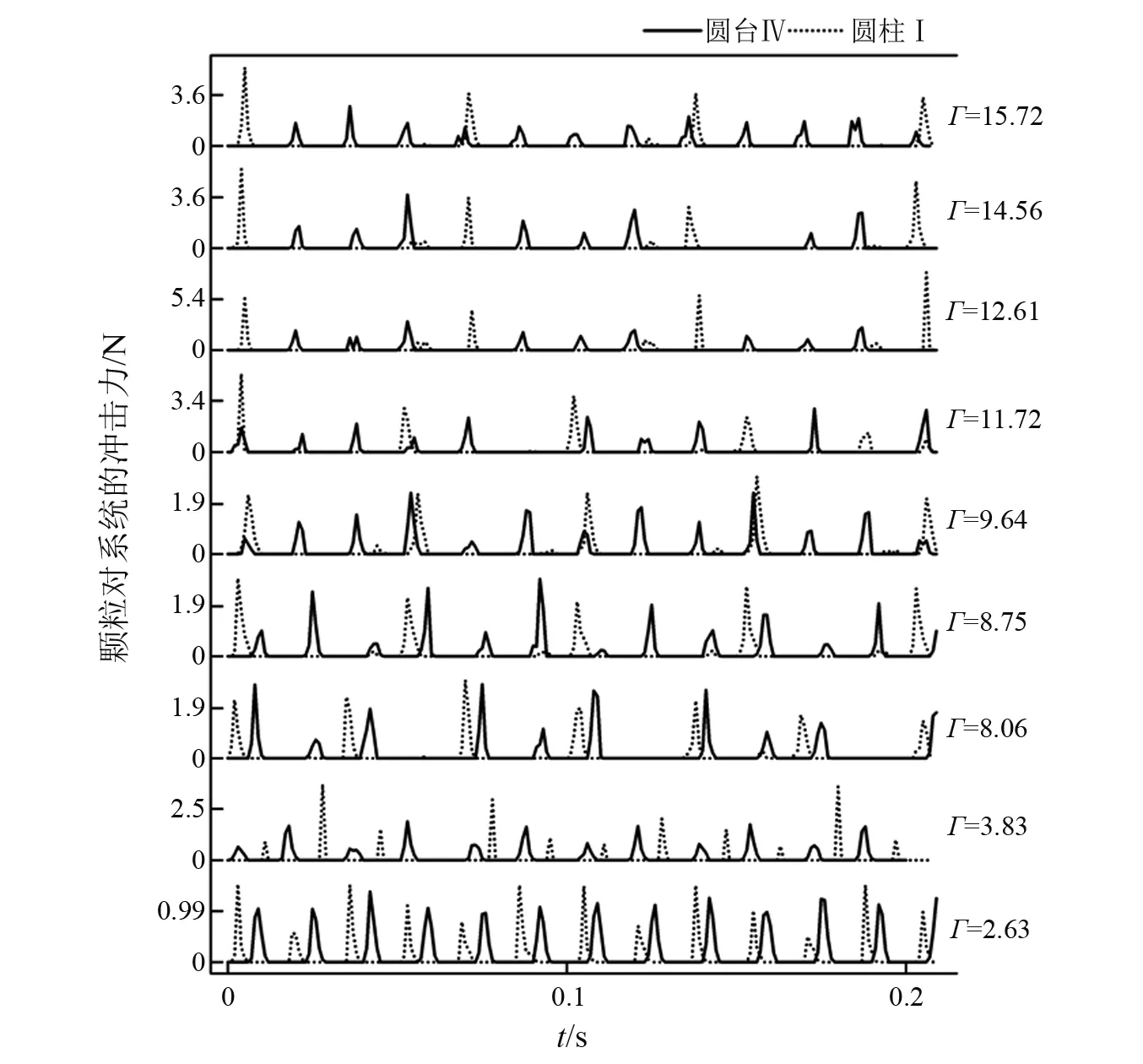
注：由下到上振动强度依次为2.63，3.83，8.06，9.64，11.72，12.61，14.56，15.72图4 颗粒对系统的冲击力随时间的变化Fig.4 The impact force of particles-system over time

以Γ=9.64为例，在一个周期内(见图5)，颗粒的运动基本可以分为四个阶段，分别是上升阶段、过渡阶段、下降阶段和冲击阶段。每个周期开始颗粒都会以振动台的速度被弹起，颗粒进入上升阶段。

在圆柱Ⅰ内颗粒运动有很强的整体性，颗粒被弹起后以一个比较大的整体速度向上飞行。由于在该振动强度下颗粒的飞行时间大于振动台的振动周期且颗粒的向上位移较大，所以在颗粒的上升阶段、第一个过渡阶段和下降过程中振动台已经做了2次“空载”运动，在冲击阶段颗粒被再次弹起时，振动台恰好完成了三个周期的运动。

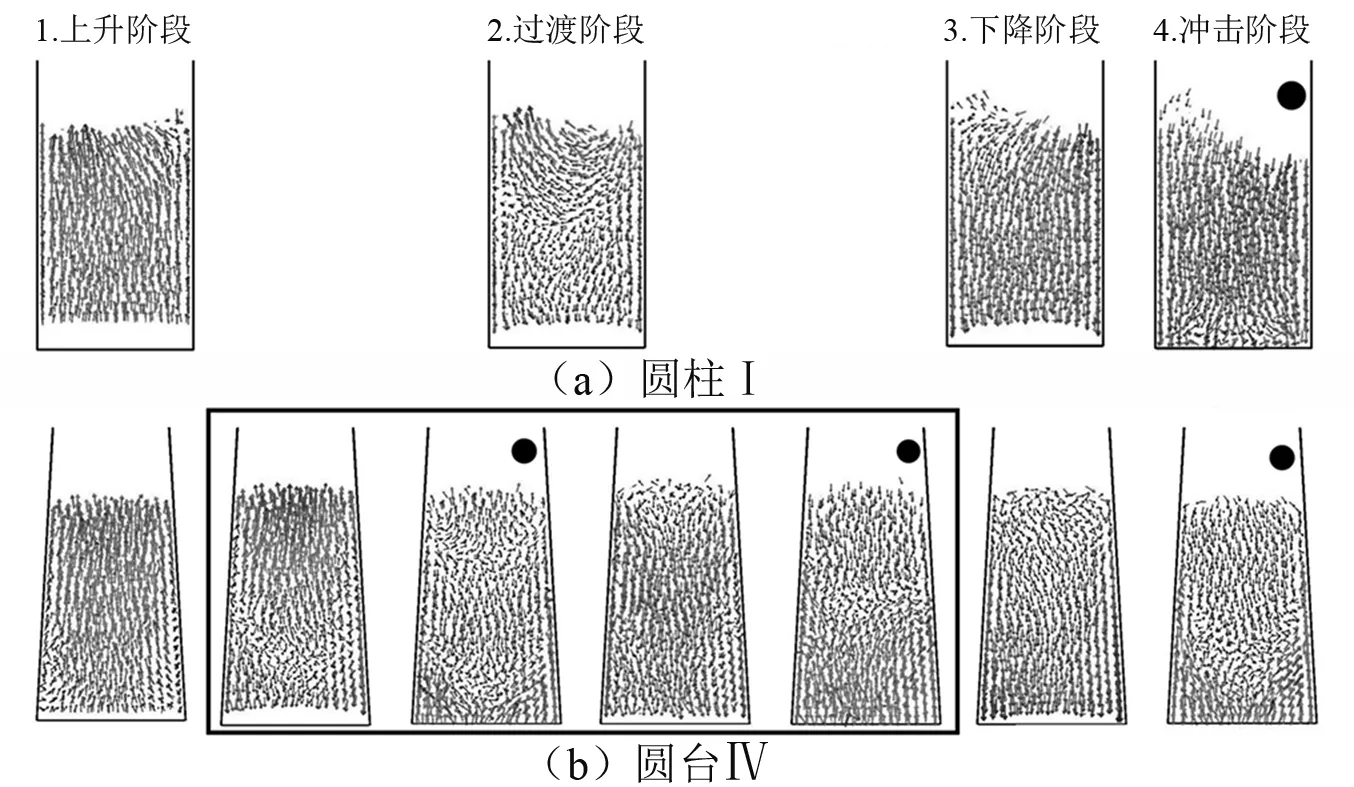
图5 容器内颗粒运动形式随时间变化Fig.5 The form of particle movement in the container changes over time

反观圆台Ⅳ内的颗粒则有明显的区域运动形式。由于在运动过程中容器底部靠近内壁处的颗粒一直受到侧壁与中心区域颗粒的强烈挤压，使其向上运动的速度分量比较小，在整个飞行过程中运动位移也比较小，所以在过渡阶段颗粒群底部的颗粒有机会与处于上升阶段的容器底部进行冲击，在该过程中容器随振动台运动了两个周期所以底部颗粒可以在过渡阶段与容器底部冲击两次(图带黑点图表示颗粒与系统底部冲击瞬时)。随后颗粒群整体进入下降阶段，在冲击阶段时，颗粒群再次有容器底部发生第三次冲击。

在其它振动条件下，同样也是由于圆台Ⅳ内位于颗粒群底部的颗粒因为受侧壁与中心区域颗粒的挤压而使其向上的位移分量较小，从而有机会与处于上升阶段的容器底部发生冲击。相比圆柱Ⅰ，圆台Ⅳ内颗粒的这种运动形式使其对冲击力的分岔现象有了一定的抑制作用。在相同的振动条件下，圆台Ⅳ内颗粒的冲击次数要多于圆柱Ⅰ内的颗粒。

2.2 冲击形式对能量损耗的影响

颗粒阻尼器的耗能主要是通过阻尼器内颗粒之间的摩擦、碰撞所引起的。由图6可知，颗粒冲击与能量

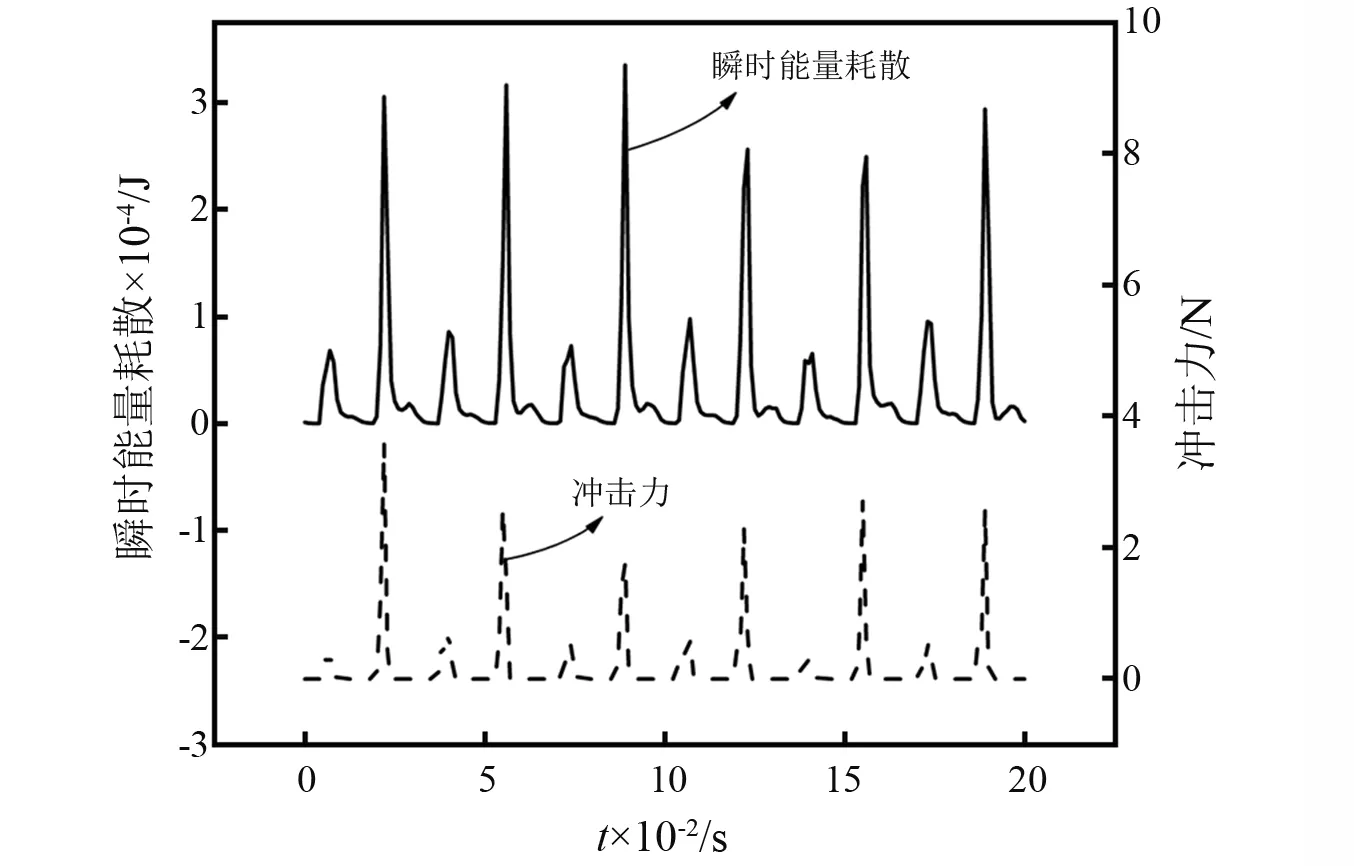
图6 圆台Ⅳ内颗粒瞬时能量损耗以及冲击力随时间的变化(振动条件：f=60 Hz, Γ=3.83)Fig.6 Instantaneous energy dissipation and impact force of particles in conical container Ⅳ over time(vibration conditions: f=60 Hz, Γ=3.83)

损耗具有一定的同步性。颗粒每次冲击容器底部时都会造成颗粒间比较强烈的碰撞与摩擦从而产生大的能量耗散。并且冲击力的大小与能量损耗量也有一定的正比关系，大冲击力对应的瞬时耗能也大，反之亦然。

通过图7可知，颗粒的能量损耗累积图呈现阶梯型，当颗粒处于飞行过程时，颗粒的能量损耗几乎为零。当颗粒与容器底部发生冲击时，在图中的能量损耗累积线就会出现一个比较明显的阶梯[22]，并且阶梯的大小与冲击力的大小存在一定的正比关系，冲击力度大能量损耗就大。在振动强度较小(Γ=2.63)时，两种容器内的能量损耗几乎相同(见图7)。但是，随着振动强度的提高，圆柱Ⅰ内颗粒出现了分岔现象，冲击力呈现“大而疏”的冲击形式，能量损耗累积阶梯也相应的呈现阶梯“大而少”型。相比于圆柱Ⅰ，圆台Ⅳ由于其颗粒运动的独特性，颗粒对系统的冲击呈“多而密”型。同样，其能量损耗累积也呈现相应的阶梯“小而多”型。值得注意的是，两种不同的冲击方式所对应的能量耗散量是不同的。圆台Ⅳ内颗粒的“小而密”的冲击方式所产生的能量损耗要远远大于圆柱Ⅰ内颗粒的能量损耗，这显示了“小而密”型冲击形式的优越性。

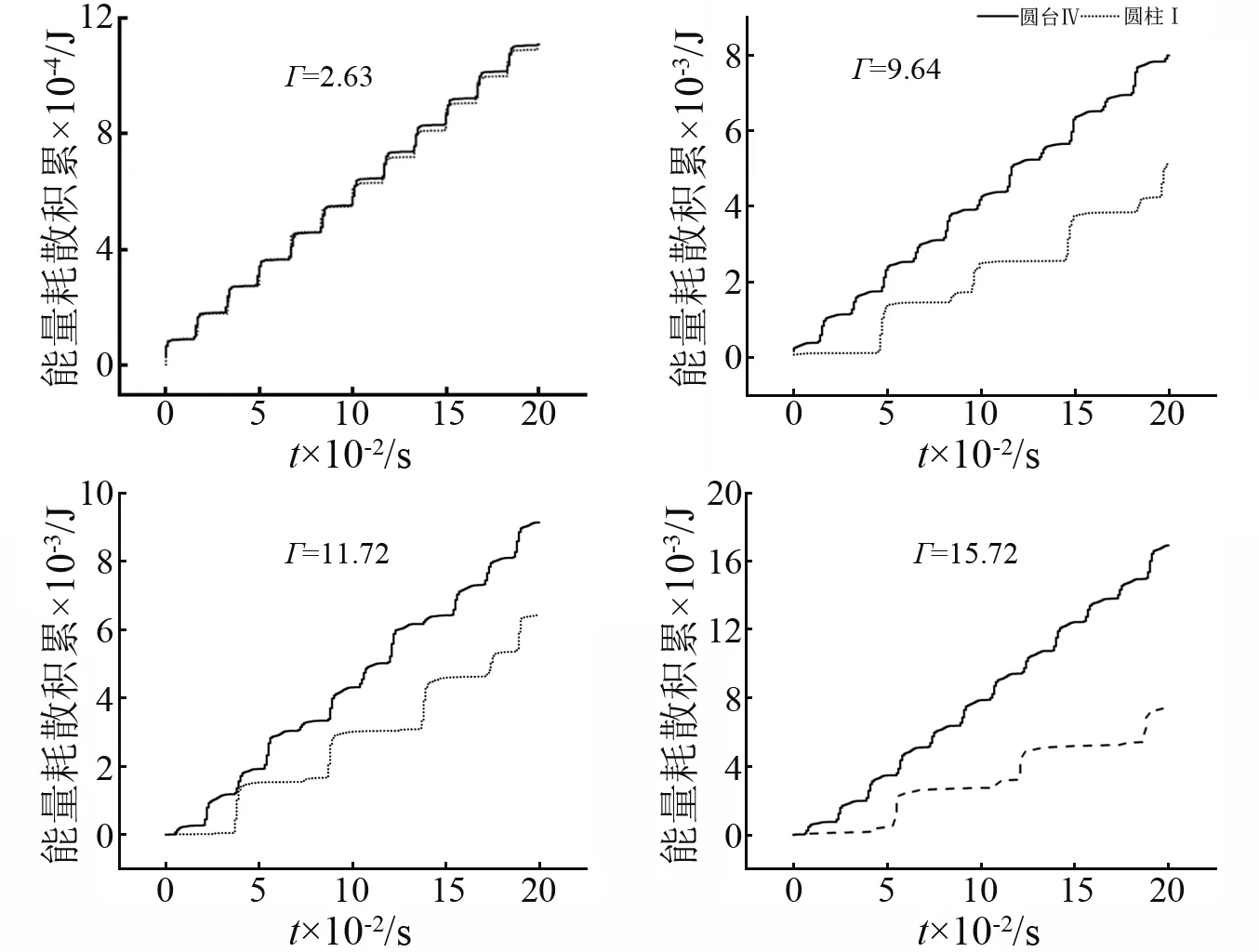
图7 0.2 s内圆台Ⅳ和圆柱Ⅰ内颗粒的能量损耗累积Fig.7 Accumulation of energy dissipation of particles in cylinder container Ⅰ and conical container Ⅳ within 0.2 s

为了充分说明冲击形式与损耗功率之间的依赖关系，本文在以上对圆柱Ⅰ与圆台Ⅳ内颗粒运动形式深入对比的基础上，进一步对比分析了不同阻尼器内颗粒床的振动与耗能特性。图8中列举了6种不同容器的颗粒阻尼器在各个振动强度下的损耗功率，并且以圆柱Ⅰ的冲击次数为基数1，得出在相同振动条件下其它形状容器内颗粒冲击次数与圆柱Ⅰ内冲击次数的比值曲线。

首先，圆柱Ⅰ和圆柱Ⅱ的曲线变化显示，尽管容器高径比发生了变化(导致颗粒填充率发生变化)，但是二者在相同振动条件下的冲击次数比值基本接近1，损耗功率在较小范围内波动。即该变化并没有对二者的冲击形式以及相应的损耗功率造成显著影响。本文中其它种类容器内颗粒的填充率均介于圆柱Ⅰ与圆柱Ⅱ的填充率之间，所以由倾角变化引起的填充率的较小波动并不是造成两类容器冲击形式以及损耗功率差异的主导因素。

总体上看，损耗功率与冲击次数比的曲线具有相同的变化趋势。在振动水平较低时(Γ=2.63，Γ=3.83)，6种阻尼器的冲击形式基本相同(冲击次数比基本为1)，损耗功率也都稳定在约0.005 W。但是，随着激振强度的提高(Γ>3.83)，圆台形容器抑制冲击力周期分岔的能力逐渐显现，圆台形与圆柱形容器所对应的冲击形式以及损耗功率也开始出现分化。尤其是在Γ≥9.64时，除圆台Ⅰ外所有圆台的冲击次数都是相同振动条件下圆柱Ⅰ内颗粒冲击次数的二倍以上，此时圆台形阻尼器相对应的损耗功率也远大于圆柱形阻尼器所对应的损耗功率。并且随着振动强度的继续增强，这两类容器的冲击形式以及损耗功率之间的差异将进一步扩大。

圆台形容器倾角的渐变(上端面直径的变化)引起了损耗功率的改变，但这种改变是基于冲击形式的变化(见图8)。例如，圆台形Ⅰ倾角较小，冲击次数介于圆柱Ⅰ、圆柱Ⅱ与圆台Ⅱ、圆台Ⅲ、圆台Ⅳ之间，颗粒床对冲击力周期分岔的抑制能力较弱，所以其损耗功率虽然高于圆柱形容器但明显小于圆台Ⅱ、圆台Ⅲ、圆台Ⅳ。不过值得注意的是，虽然圆台Ⅲ、圆台Ⅳ的倾角比圆台形Ⅱ要大，但是由于倾角的变化并未导致冲击形式的显著变化(冲击次数与圆台Ⅱ相差较小)，所以其损耗功率仍没有本质的变化。综上，圆台形倾角的变化对损耗功率的影响取决于倾角的改变是否导致冲击形式的变化，进一步说明，冲击形式才是导致损耗功率发生显著变化的根本原因。