高速动车组车体模态特性分析*

王 鹏， 陈恩利， 惠美玲， 蔡大军

(1.石家庄铁道大学交通运输学院 石家庄，050043)

(2.中车唐山机车车辆有限公司产品研发中心 唐山，063035) (3.燕山大学机械工程学院 秦皇岛，066000)

引 言

合理的车体结构不仅具有良好的模态特性，还能降低车体振动对车辆运行品质和结构安全的影响[1-4]。为保证高速动车组运行中具有良好的车体结构抗振特性，需对车辆进行结构模态分析[5]，确定结构固有频率和振型。高速动车组车体按照轻量化设计原则进行结构设计，在设计初期阶段，车体质量最小是设计目标，但质量减少可能会使车体刚度相应降低，并导致车体模态频率不能满足相关标准[6-9]，甚至会出现车体模态频率偏低，与转向架发生共振等问题。通过模态分析得到车体结构低阶振型及频率，用以判定其振动特性能否满足设计要求[10],进而为车体结构优化设计及新产品开发提供理论依据。

1 车体结构及技术参数

高速动车组车体使用的材料主要是铝合金，由大型中空铝合金型材组焊而成[11]，具有良好的防腐性能。其承载结构为筒型整体承载结构，这种结构不仅使车体的质量较轻，而且能够有效地减少车体结构的零部件种类，降低生产成本，改良制造工艺性，同时具有较好的截面刚度特性和较高车体强度，从而可提高动车组车体整体刚度、乘坐舒适性和安全性。

根据动车组车体外形分为头车和中间车两种，车体由铝型材和板材通过插接、搭接、对接等形式焊接成大部件，再经组对、拼接成整个车体。中间车车体主要由底架、侧墙、端墙、车顶及车体附件等部分组成。头车设有司机室，司机室采用较大截面的有压筋墙顶板与梁柱组焊而成，参与车体整体承载。如果发生低速撞车事故，头车的结构设计能够给司机提供一个安全空间。车体主要技术参数见表1。

表1 中间车主要技术参数

2 模态分析理论及有限元模型

2.1 模态分析算法原理

根据振动理论，多自由度系统以某一固有频率振动时所呈现的振动形式称为模态。结构设计中，一般要进行模态计算验证结构的合理性，以便采取主动性控制措施。

车体在运行过程中受多种激励共同作用，属于复杂的力学系统，一般采用有限元法确定其固有频率和振型。车体结构经过有限单元离散和变分，可得车体振动动力学方程[12]为

(1)

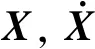
模态与外部载荷条件无关，即F=0，并忽略阻尼C影响，可得系统自由振动方程为

(2)

自由振动时，结构上各点作简谐振动，假设简谐振动方程为

与无吊挂设备的整备状态计算结果相比，设备刚性吊挂对车体菱形模态影响很小，但使底架1阶垂弯模态频率降低了0.7 Hz。

X=Φejωt

(3)

无吊挂设备时车体整备状态质量为28 t。前8阶模态分析结果见表3，车体结构典型模态振型云图如图3所示。

将式(2)代入式(3)可得

(K-ω2M)Φ=0

(4)

由上式存在非零解，可得

|K-ω2M|=0

(5)

得到车体各阶模态频率ωi(i=1，2，…，n)和相应振型Φi(i=1，2，…，n)。

2.2 有限元模型

我国《200 km/h及以上速度级铁道车辆强度设计及试验鉴定暂行规定》要求整备车体1阶弯曲频率应不低于10 Hz[13]。笔者利用HyperMesh软件建立车体有限元模型，通过ANSYS有限元软件进行分析计算。

驱动软件总体控制流程如图9所示，首先进行控制器内相关外设的初始化，然后对射频通道1上本振芯片进行配置。直等到确认射频通道1的本振频率锁定后，则对射频通道2上本振芯片进行配置。当射频通道2上的本振频率锁定后，控制器进入休眠状态。假如有外部中断将控制器唤醒，则根据如图9所示流程再次依次配置射频通道1与射频通道2上的本振频率。

动车组车体的零部件基本上都是薄壁构件，整车结构采用四边形薄壳单元模拟，对重要部位进行局部网格细划。建模时，车体的内装、门窗、座椅等重要部件都以质量点方式附加到实际的安装基点上。同样，车下吊挂设备采用质量点刚性耦合(rbe3单元)方式吊挂在车体上，确保模型接近车体实际情况。

结果表明：振型分布与纯铝合金车体时的振型分布基本一致，第1阶模态振型为中部菱形振动，车顶与侧墙连接处变形较大，说明刚度不足；第2阶模态由车体壳结构状态时的整体呼吸加底架弯曲振动演变为底架1阶垂向弯曲振动；第3阶模态为车体1阶扭转振动，同车体壳结构1阶扭转振型一致，形变主要在一位端。

图1 中间车车体有限元模型

3 车体有限元模态分析

3.1 车体模态计算结果

将车体有限元模型导入ANSYS软件，分别计算了车体壳结构、无吊挂设备时整备车体、含吊挂设备时整备车体3种质量条件下的车体振动模态。

本研究结果显示，总TAMs密度或肿瘤基质内TAMs低，NSCLC患者5年生存率高，与良好预后相关；而在肿瘤细胞团内，TAMs的密度低，NSCLC患者的5年生存率低，提示预后不良。这证实了在大多情况下，TAMs在微环境中表现出免疫抑制的作用，不同分布的TAMs密度对临床NSCLC患者的预后有指导作用。

3.1.1 车体壳结构模态

从饮水安全供水工程看投资计算应注意的问题………………………………… 李兴运，郑子升，徐俊霞(10.54)

车体壳结构即无设备空车状态的车体质量为10.08 t，前8阶模态分析结果见表2，典型模态振型云图如图2所示。

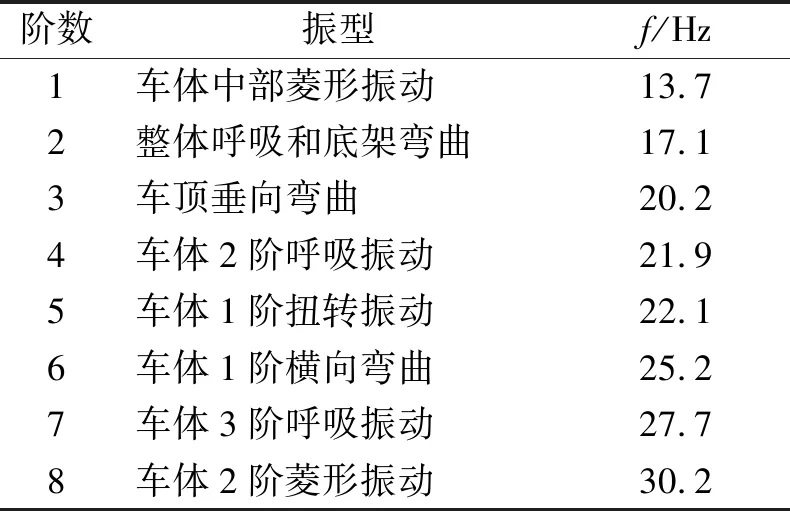
表2 车体壳结构计算模态

图2 车体壳结构振型图

结果表明：第1阶模态振型为中部菱形振动，主要表现为车顶和底架的横向反向振动；第2阶模态为整体呼吸和底架弯曲振动，主要表现为车体中的车顶、侧墙的振动，底架弯曲弹性变形较小，说明底架垂弯刚度良好；第5阶模态振型为车体1阶扭转振动，车体一位端车顶弹性变形较大。

3.1.2 无吊挂设备时车体整备模态

其中：Φ为振型向量；ω为模态频率。

3)Client发送协议报文信息。Client在发送请求命令之后，还要以协议报文的形式向服务器发送请求的具体参数。

图3 无吊挂设备整备振型图

表3 无吊挂设备时车体整备模态

Tab.3 Car body modal without hanging

阶数振型f/Hz1车体中部菱形振动 9.62底架1阶垂向弯曲11.53车体1阶扭转振动14.44车顶弯曲+底架弯曲14.85局部呼吸+底架2阶弯曲15.26车体1阶横弯振动16.97其他模态17.88其他模态20.1

整车有限元模型共有单元664 318个，节点共有555 120个。计算时取：弹性模量E=70 GPa；泊松比μ=0.334；密度ρ= 2.71×103kg/m3。有限元模型如图1所示。

4)互异性检验。整备车体互异性应满足

含吊挂设备时车体整备状态质量为34.8 t，设备采用刚性吊挂方式连接在车体上，与车辆实际重量相符。前8阶模态分析结果见表4，典型模态振型云图如图4所示。

结果表明：此时模态振型与前2种工况下振型分布基本一致，即第1阶模态振型仍为中部菱形振动；第2阶模态为底架1阶垂向弯曲，模态频率为10.8 Hz，符合设计标准；第3阶车体扭转振动主要表现在一位端，说明空调口处局部变形较大，必要时应增加空调安装位置的刚度。

表4 含吊挂设备时车体整备模态

图4 含吊挂设备整备振型图

全碳纤维复合材料车体为薄壁筒形整体承载结构，主要尺寸如下：车体基本长度为19 000 mm，车体宽度为2 800 mm，车体顶面距轨面高度为3 478 mm。

3.2 设备吊挂位置对模态频率的影响

为研究设备吊挂位置对车体模态的影响，在车下仅刚性吊挂一个设备，改变吊挂位置，分析车体模态的变化规律。主要考虑了设备距离车体中心4，1.8，0，-2，-3.8和-5 m共计6种工况。车体前6阶模态分布如表5所示。

3) 阻尼比测定。取1阶弯曲自振频率半功率带宽Δωr，按式(8)计算该阶阻尼比

表5 设备在不同安装位置时车体模态频率

图5 吊挂位置对模态频率影响曲线

图6 车体模态振型图(距车体中心4 m)

由图5、图6可知，第2阶振型为底架1阶垂弯，第3阶振型为车体1阶扭转。设备刚性吊挂时，随着设备靠近车体中心，模态频率逐渐降低，吊挂位置对车体的垂向振动和扭转振动影响越大。

5）孔口管安设:用CS（水泥、水玻璃）砂浆埋设φ42mm孔口管，在管口安装φ76mm球形闸阀，作为封闭钻孔中可能会出现的涌水。

结合弹性梁的振动理论可知，车体中心处的弹性位移最大，越靠近车体两端其弹性变形越小。当设备刚性吊挂且靠近车体中心安装时，相当于增加了车体中心位置处的模态质量，而模态刚度基本不改变，因此模态频率降低。

3.3 设备吊挂点数对模态频率的影响

为分析车体模态的变化规律，车下仅刚性吊挂一个设备，改变设备的吊挂点数，考虑了4，6，8和12个吊挂点联接工况。车体结构前6阶模态频率如表6所示。

由表6可知，设备吊挂点由6个增至8个时，车体第1阶模态频率提高了0.5 Hz；吊挂点增至12个时，第1阶模态频率提高了1.5 Hz，主要变为底架中部的弯曲振动和侧墙的呼吸振动，模态振型如图7所示。其余模态频率也有所提高，但不如第1阶模态频率增幅显著。各阶模态频率随吊挂点数的变化曲线如图8所示。

表6 设备采用不同吊挂点数目时车体模态频率

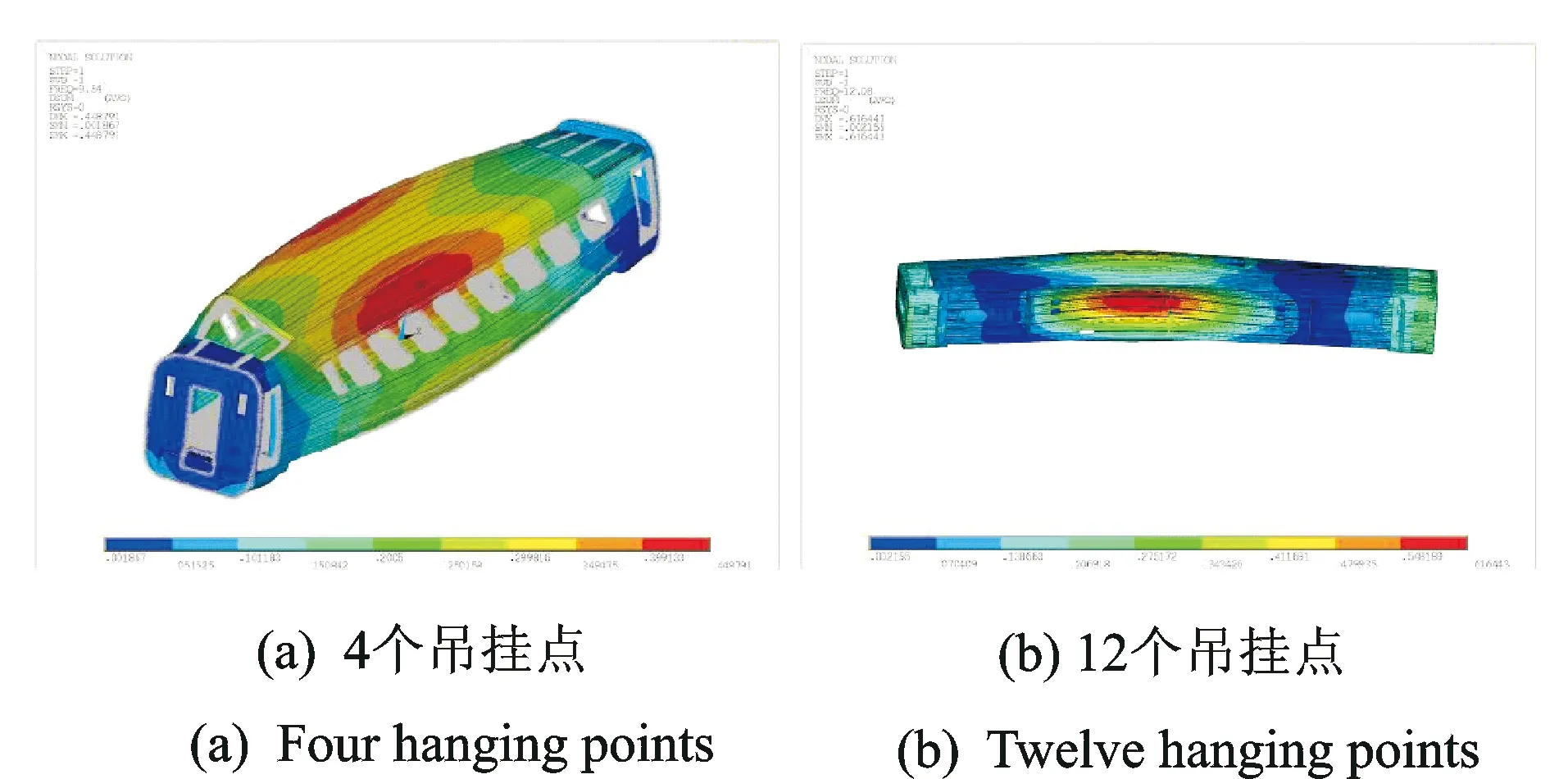
图7 车体第1阶模态振型图

图8 吊挂点数对模态频率影响曲线

由图8可知，当设备吊挂点增加时，车体第1阶模态频率逐渐提高，主要是由于设备采用刚性联接，相当于增加了底架的局部结构刚度，抑制了底架的低阶弹性模态，从而提高了模态频率。

4 整备车体模态试验

4.1 试验原理

对于结构复杂的车体进行模态试验，采用多点激扰多点测量方法可得到较准确的模态。

2.2两组皮肤炎恢复时间、护理满意度比较 观察组皮肤炎恢复时间(104.27±12.43)d,对照组为(163.53±13.65)d;观察组满意率为95.12%(39/41),对照组为77.50%(31/40),观察组皮肤炎恢复时间较对照组短,满意率高于对照组,差异均有统计学意义(t=20.44,X 2=5.36,P<0.05)。

1) 固有频率测定。利用式(6)估计频响函数，利用多参考最小二乘复频域法确定模态函数

H1(f)=GXF(f)/GFF(f)

(6)

2) 振型测定。在车体自振频率附近进行多点激振，测定各响应点的加速度幅值并归一化，由此得到模态固有振型，利用式(7)检验振型的有效性

首先，这两个结构后面都必须跟动词原形。be going to 结构中的be 一般有三种形式，即：am，is，are。当主语是I 时用am；当主语是he／she／it或其他第三人称单数时用is；当主语是复数时用are。

(7)

其中：Xi(ω)为第i自由度频响函数；ReXi(ω)为第i自由度频响函数实部；Mi为第i自由度模态质量。

由表5可知，设备距车体中心线 - 4～4 m范围内变化时，各阶模态频率变化范围不超过0.5 Hz，其中第2阶、第3阶模态频率变化显著，变化曲线如图5所示。工况1的第2、第3阶振型云图如图6所示。

ζr=Δωr/2ωr

(8)

其中：ωr=2πfr为角频率。

3.1.3 含吊挂设备时车体整备模态

Hij(ω)=Hji(ω)

(9)

其中：Hij(ω)为第j点激励、第i点响应的频响函数；Hji(ω)为第i点激励、第j点响应的频响函数。

4.2 试验方法

模态试验中被测试对象为某中间车含吊挂设备时车体整备状态。车体支撑为原转向架及空气弹簧，空气弹簧充气压力符合整备车辆技术要求。

2.拓宽企业融资渠道。深化债券市场融资功能，引导企业通过发行企业债、公司债、中期票据、资产支持票据、短期融资券、超短期融资券、项目收益债等融资方式，扩大融资规模；发挥政府投资引导基金作用，支持产业链核心企业发起、引导社会资本共同参与设立产业创投基金，为产业链上下游企业提供资金支持。鼓励有条件的民营企业联合发起设立民营资本投资公司。设立广西并购引导基金，推动工业企业重组整合壮大。积极争取投贷联动试点，大力推动市场化法治化债转股工作。

在开始基西米河生态修复的基础上，组织人员成立了专门的研究机构，制定和提出了奥基乔比湖生态修复、大沼泽地恢复及建设、佛州湾生态修复、入海河口治理等一系列计划、方案，并在每个项目上投入了大量经费。

根据车体特点，沿车体长度方向基本均匀选取10个截面反映车体整体振动形态，每个截面布设8个加速度传感器测点。每个测点测试垂向和横向的加速度，传感器采用ICP加速度传感器，传感器位置和整备车体坐标系定义如图9所示。整备车体模态试验组成系统如图10所示。

在再生混凝土中适量掺入钢纤维，可以增强其抗拉、抗折、抗弯和抗剪等性能。由于直接进行混凝土的轴心抗拉试验很繁琐，因此大多数的研究是采用劈裂抗拉试验取代轴心抗拉试验。由于现行的钢纤维再生混凝土(Steel Fiber Recycled Aggregate Concrete，SFRAC)试验方法仍沿用劈裂抗拉强度来确定轴心抗拉强度，但并未说明如何将劈裂抗拉强度换算成钢纤维再生混凝土的轴心抗拉强度。因此，本文设计了一种新型的钢纤维再生混凝土轴心抗拉试件——哑铃型试件，在普通试验机上获得混凝土的轴心抗拉强度[4]。

图9 传感器安装位置示意

图10 模态试验系统组成示意图

模态试验依据《机车车辆动力学性能台架试验方法》进行，采用4台激振器作为模态试验的激振源，激励点位于车体底架两端刚度较大的位置。

4.3 试验结果

试验采用2～40 Hz猝发随机信号进行激励，设置采样频率为1 024 Hz，最终得到测试数据。利用polymax法对试验数据进行处理，得到相应的模态频率、振型和阻尼比。整备车体模态试验结果见表7，模态振型如图11所示。

表7 车体模态试验结果

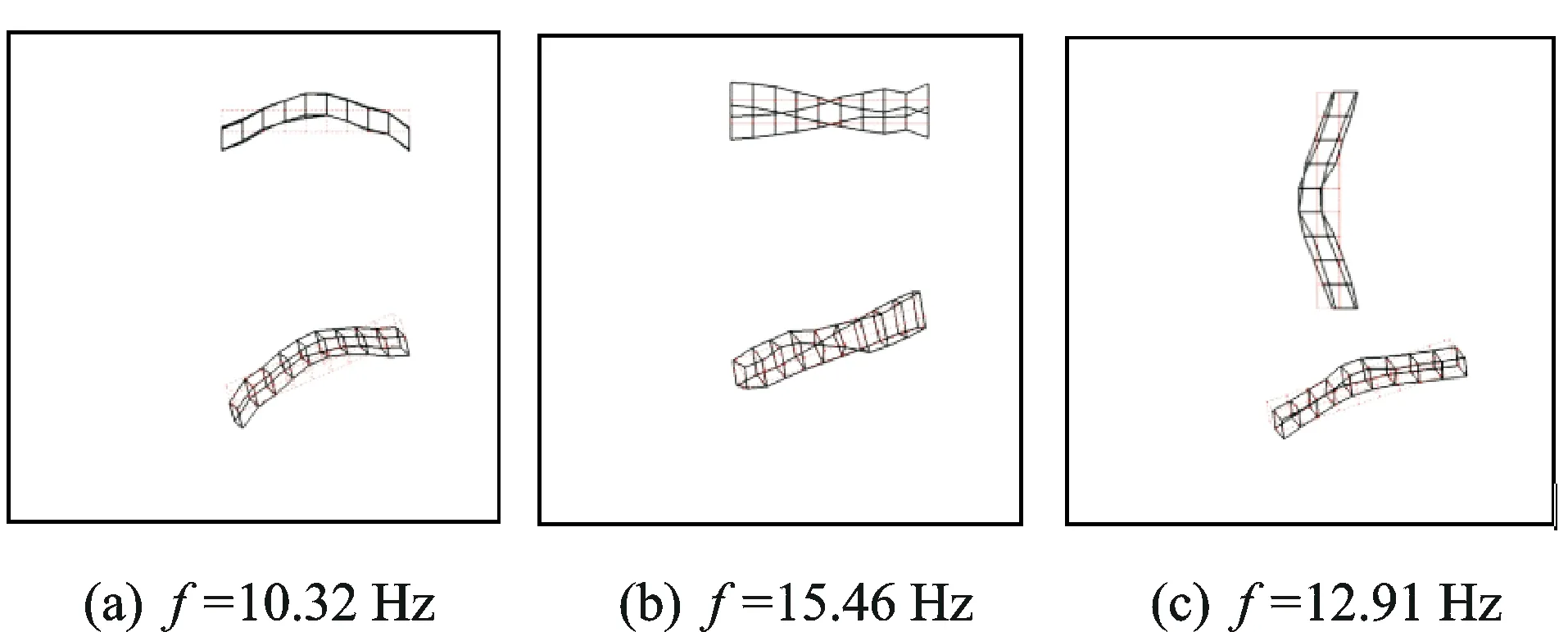
图11 车体模态试验振型图

对比仿真与试验结果可以看出，两者具有很好的一致性，说明车体有限元模型能够反映车体结构特性和实际承载能力。底架1阶垂弯模态频率相差0.48 Hz，误差约9.69 %；车体1阶扭转模态频率相差0.99 Hz,误差约7.67 %；车体横向弯曲模态频率相差0.64 Hz，误差约4.14 %。底架垂弯频率误差较大，主要是由于车体模型简化与实际结构有一定差异，板材加工、车体装配及试验测试等不可控因素都会使试验与仿真结果产生一定误差。

同样道理，孕前孕妈妈体重较重，意味着自身体内脂肪较多，所以在24周前增重3千克即可，因为还有2千克左右的间质其实孕妈妈已经储备了；如果孕前孕妈妈体重较为理想，到24周增重4千克左右也可以了，适当地储备了一下营养；孕前较瘦的孕妈妈，24周前可以增重5～6千克，是为了弥补孕前的营养储备不足。所以体重是一个行之有效的监测能量是否充足的最简单的方法，但称量体重的方法一定要对，那就是早晨起床，空腹，排空二便，穿同样的衣服，最好是内衣，在同一个秤上称重，这样做是为了称出净体重，减少其他因素对体重的影响，这样的体重才有可比性，否则由于外在因素的影响，不能准确反映体重的增加幅度。

5 结 论

1) 各质量状态下车体模态振型分布基本一致，车体整备模态垂弯频率满足设计标准。设备吊挂位置对底架垂弯和车体扭转振动频率影响较明显，设备越靠近车体中心，对提高车体垂向振动的相关模态效果越好。当安装在车体中心时，车体结构模态频率降低，但不超过0.5 Hz。吊挂点数不同对车体第1阶模态影响明显，随着吊挂点数目的增加，车体第1阶模态中部菱形振动被抑制，模态频率逐渐提高，其余模态频率也有所提高，但不如第1阶模态频率增幅显著。

考虑到煤炭矿区规划分阶段实施，评价指标提出了阶段指标值，即近期(2010年)、中期(2015年)及远期(均衡期)目标值，详见表1。

2) 车体模态计算结果与试验结果具有很好的一致性，验证了模型的正确性，说明车体有限元模型能够反映车体结构特性和实际承载能力。总之，通过模态计算与模态试验对比研究，可以为车体优化设计提供理论依据，进一步提高车辆运行品质和行车安全。