车桥耦合振动的拱桥吊杆应力冲击系数分析*

朱志辉， 罗思慧， 张 磊， 王力东， 余志武， 孟 鑫

(1.中南大学土木工程学院 长沙，410075) (2.中南大学高速铁路建造技术国家工程实验室 长沙，410075)

(3.中国铁道科学研究院集团有限公司铁道建筑研究所 北京，100081)

引 言

系杆拱桥因其良好的跨越能力和优美的造型得以广泛应用[1]，吊杆是其关键受力构件，对拱桥安全性具有重要影响。吊杆失效轻则引起吊杆静张力重分布，对拱桥结构整体受力安全产生不利影响，重则导致桥面坍塌等恶性事故[2]。车辆荷载产生的冲击作用会导致吊杆在远低于其静力强度的情况下发生疲劳失效[3]。因此，研究车辆作用下的拱桥吊杆应力冲击系数，对桥梁检测、评估以及维护等工作具有重要意义。Huang等[4]对中承式钢管混凝土拱桥在高速公路车辆作用下主梁的冲击系数进行了研究。Shao等[5]研究了桥梁粗糙度和车速对吊杆应力冲击系数的影响。Malm等[6]指出铁路拱桥吊杆约60%的变幅循环应力源自车桥振动。因此，为准确分析移动列车作用下的吊杆冲击效应，应基于列车-轨道-桥梁耦合系统模型开展研究。朱劲松等[7]采用自主编制的公路车辆-桥梁耦合振动计算程序分析了中下承式钢管混凝土系杆拱桥中结构阻尼、路面不平顺度、车速及车重对吊杆应力冲击系数不均匀性的影响。朱志辉等[8]基于车-线-桥耦合动力学模型，采用虚拟激励法从随机振动的角度研究了车速和轨道不平顺对重载铁路拱桥吊杆应力的影响。通常在桥梁局部构件设计时，一般采用影响线加载得到局部活载杆件的静应力，并通过动力放大系数考虑动力效应[9]，该方法被多个国家的规范所采用。但是，高速铁路桥梁动力系数受车速等因素影响显著，上述方法不够准确[10]，因此需要进一步针对高速铁路拱桥吊杆应力冲击问题开展理论研究。

现场测试及结构健康监控是评估桥梁动力响应及冲击系数的另一有效手段[11]，通过试验获得桥梁基本动力特性，也可有效提高数值仿真精度。相对于传统位移和吊杆应力测试方法，地基微波雷达具有远程非接触、环境因素干扰小、测试精度高和不受天窗时间限制等优点，在高速铁路大跨度桥梁变形监测上具有较好的应用[12]。Maizuar等[13]将雷达测试技术与数值模型结合，用于检测桥梁固有频率的变化。黄声享等[14]将地基微波干涉雷达与GPS技术进行对比，表明地面微波干涉雷达技术可以精细地测量桥梁挠度的动态变化，并反映其动态变形特征。

针对上述问题，笔者主要研究了移动列车作用下不同行车条件对高速铁路系杆拱桥吊杆应力冲击系数的影响规律。首先，基于车桥耦合动力学理论建立了列车-轨道-桥梁耦合系统模型；其次，以海南东环铁路万宁系杆拱桥为例，采用地基微波雷达测试了该桥的行车动力响应，并基于试验数据验证了万宁桥理论模型的正确性；最后，基于该模型研究了行车速度和轨道不平顺对吊杆应力冲击系数的影响。

1 吊杆应力冲击系数计算模型

1.1 列车-轨道-桥梁耦合系统模型

列车-轨道-桥梁耦合系统模型分为车辆和轨道-桥梁两部分子系统。单节车辆简化为由1个车体、2个转向架、4个轮对以及一系和二系悬挂组成的质量-弹簧-阻尼器系统，考虑车体、转向架的沉浮和点头自由度以及轮对的沉浮自由度，基于刚体动力学方法建立10自由度车辆模型。基于有限元方法建立轨道-桥梁子系统，两子系统之间通过线性Hertz轮轨接触模型进行耦合，则车辆-轨道-桥梁耦合系统动力方程[15-16]表示为

(1)

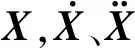
矩阵和向量的具体形式可参考文献[17]，采用Newmark-β法对式(1)进行求解。

1.2 吊杆应力冲击系数

基于试验测量或列车-轨道-桥梁耦合系统模型计算得到吊杆两端节点的位移时程Xtop(t)和Xbot(t)，则吊杆动应力时程σd(t)表示为

(2)

其中：L和E分别为吊杆长度和弹性模量。

《铁路桥梁检定规范》(铁运函[2004]120号)指出，动力系数为列车运行对结构产生的动态反应与静态反应之比，则吊杆应力动力系数可表示为

1+μ=σdmax/σsmax

(3)

其中：μ为吊杆应力冲击系数；σdmax为动力分析时吊杆最大动应力；σsmax为吊杆最大静应力。

根据《铁路桥涵设计基本规范》(TB10002.1-2005)，吊杆动力系数(dynamic coefficient, 简称DC)可以写为

(4)

其中：α=4(1-h)≤2，h为填土厚度；对于局部活载杆件，L0为影响线加载长度。

基于Matlab语言编制了车桥耦合振动的吊杆应力冲击系数计算程序，计算流程如图1所示。

图1 吊杆应力冲击系数求解流程

2 地基微波雷达测试原理及试验验证

近年来，雷达技术逐渐应用于桥梁挠度测量、结构损伤检测和动态变形监测等领域[18]。地基微波雷达测试原理由线性调频连续波(linear frequency modulated continuous wave, 简称LFMCW)[19]、相位干涉测量技术和位移投影技术[12]组成。LFMCW型雷达具有低截获概率特性，测试精度受目标物体运动速度影响较小，波束抗干扰能力强，能够进行多目标精准识别和远距离测量[20]。地基微波雷达工作原理如图2(a)所示，频率带宽为B的微波信号以时间周期T循环重复发射，经被测目标反射后的回波信号与发射信号之间存在τ的时间延迟，将二者混频后得到的差拍信号进行解调得到目标位移。在初始频率为f0的情况下，差拍信号vB(t)[20]可表示为

(5)

其中：η为信号衰减系数；j为虚数单位。

根据差拍信号的中心频率fB和电磁波波速c即可得到目标距离R

R=fBcT/2B

(6)

图2(b)所示的相位干涉测量技术可以实现高精度的动态位移测量[12]。被测目标在电磁波传播方向上的运动导致了物体表面反射信号之间的相位差Δφ，则沿波传播方向位移dr可以表示为

(7)

其中：f为地基微波雷达的工作频率，可取10 GHz /24 GHz ISM(ISM为国际通用的工业、科学和医学雷达工作频段)。

由于雷达的发射波长为厘米级，通过相位差估计目标位置可以达到很高的精度。

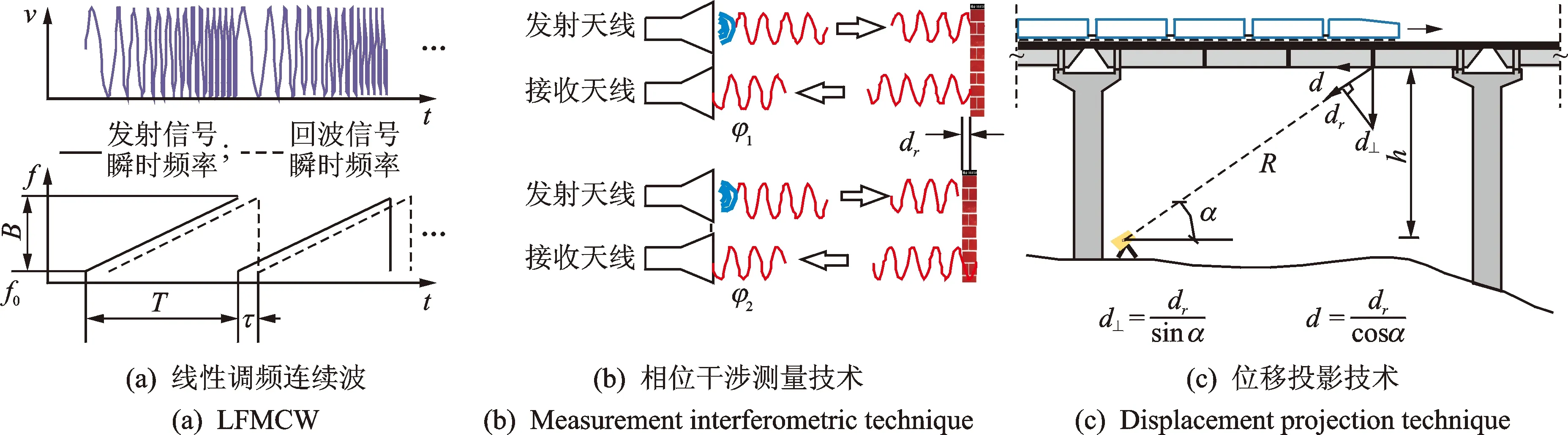
图2 地基微波雷达测试原理

在实际测试中，地基微波雷达测量结果为沿波传播方向的径向位移，还需基于如图2(c)所示的位移投影技术[12]将其转化为垂向和水平位移变化值。雷达测试系统直接测量得到距离变化量dr和仰角α，通过几何计算即可得到垂向位移d⊥和水平位移d。

本研究雷达采用B=300 MHz的步进频率波形，探测视角不小于30°，最大测距可达750 m，最高采样频率为200 Hz。在动态变形检测系统中，通过调整测量距离和工作频段可使位移估计精度优于0.01 mm。

为验证地基微波雷达位移测试精度，以图3所示的移动模型车过5跨简支梁为测试对象，在试验室内分别采用动态位移传感器(linear variable differential transformer, 简称LVDT)和地基微波雷达对简支梁跨中位移响应进行对比测试，室内试验布置如图4所示。其中LVDT量程为50 mm，非线性误差为0.25%。从图5给出的2种方法测试得到的第3跨跨中竖向位移时程对比结果可以看出， 2种测试方法的位移测试时程曲线结果吻合较好。其中动态位移传感器和地基微波雷达测量的跨中位移最大值分别为0.578和0.597 mm，二者误差仅为3.29%，表明地基微波雷达可以较好地应用于桥梁动挠度的试验测量。

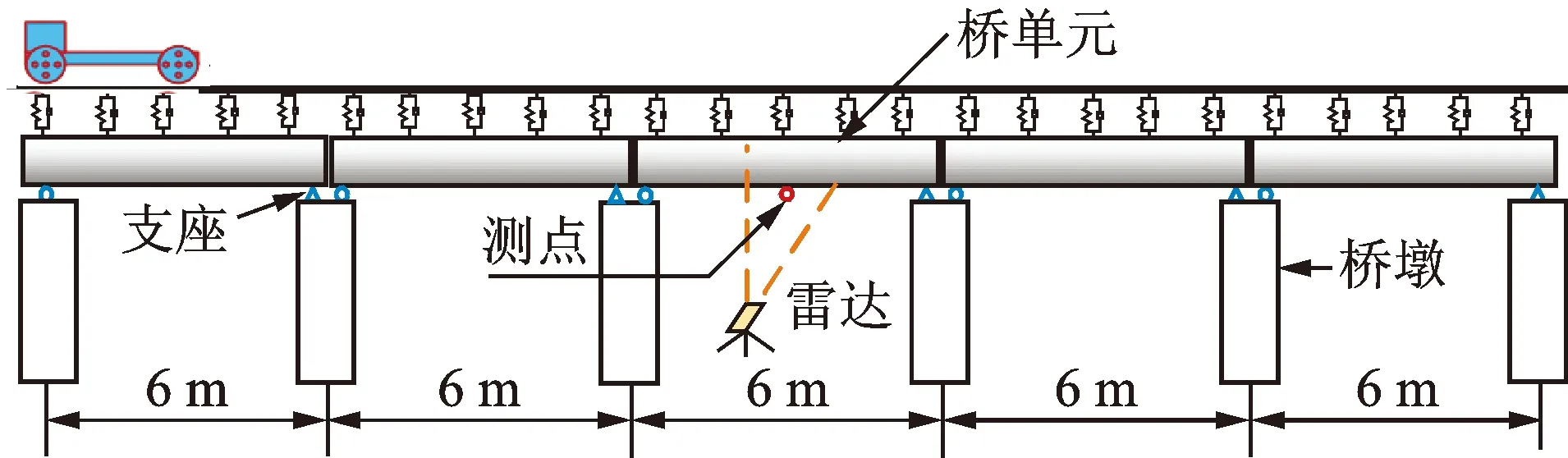
图3 5跨简支梁试验示意图

图5 跨中测点位移时程曲线对比

3 万宁桥现场行车动力响应试验

3.1 桥梁概况

海南万宁系杆拱桥为南北走向(海口—三亚)的预应力混凝土下承式系杆拱桥，桥梁全长为63.5 m，跨度为61.5 m，拱轴线为二次抛物线(y=x2/76.875)，矢跨比为1/5。万宁桥桥型布置及吊杆编号如图6所示。线路等级为铁路I级，桥面铺设双线有砟轨道，道砟厚度为0.63 m，线间距为4.6 m，设计时速为250 km/h。梁体混凝土重度γ取26.25 kN/m3，二期恒载按210 kN/m考虑。桥梁主梁、拱肋、横撑和挡渣墙均采用C55混凝土。桥面上共有18根间距为6 m的钢绞线柔性吊杆，截面面积为1.169×10-2m2，抗拉强度为1 860 MPa。拱肋为钢筋混凝土构件，高为2.0 m，拱肋净宽为1.0 m。

3.2 万宁桥试验方案

万宁桥上跨城市主干道，且处于通车运营阶段，地基微波雷达可做到非接触多测点的位移精确测量，相较于传统测量方法更为简便。2017年1月，采用地基微波雷达对万宁桥在CRH1A型列车通行状态下的动态变形进行了测试，并根据桥梁动态响应数据分析其自振频率和吊杆动应力。测点布置如图7所示，CD1为主梁3/10跨行车侧测点，CD2和CD3分别为跨中行车侧5#吊杆顶端测点和底端测点。

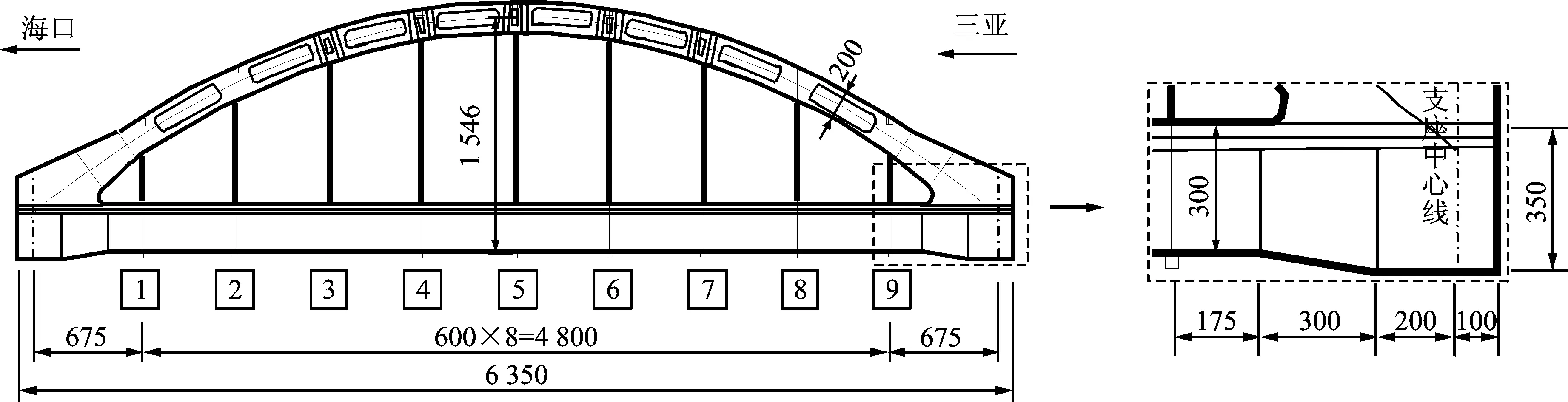
图6 万宁桥桥型布置图(单位：cm)

图7 万宁桥动力测试示意图

现场测试如图8所示，将地基微波雷达置于万宁桥下城市主干道上，调整角度对准试验测点后进行动态变形测量。地基微波雷达工作频段为24 GHz ISM，采样频率为200 Hz。根据试验方案对万宁桥进行了多组试验，表1给出了其中2组测量试验的工况信息。工况1可根据明显的余振响应得出桥梁自振特性；工况2同时测量了吊杆两端位移时程响应，可计算得到吊杆动应力时程曲线。

图8 现场行车试验及测点位置

图9 工况1的CD1测点位移

3.3 测试结果分析

从图9给出的工况1的CD1位移时程曲线可以看出，列车经过时吊杆产生了明显位移波动，CD1位移最大值为0.903 mm。根据列车出桥后的桥梁自由振动时程曲线，可计算得到万宁桥阻尼比为0.039 6，1阶竖向自振频率为3.373 Hz，大于《高速铁路设计规范》(TB10621-2014)规定的最小限值2.058 Hz(23.58L-0.592)，表明万宁桥刚度满足高速铁路的设计要求。

图10给出了由工况2的CD2和CD3之间的相对位移变化值计算得到的行车侧5#吊杆应力时程曲线，吊杆应力最大值为16.837 MPa，吊杆应力冲击系数为0.093，小于《铁路桥桥涵设计基本规范》推荐公式所计算的吊杆应力冲击系数0.211。

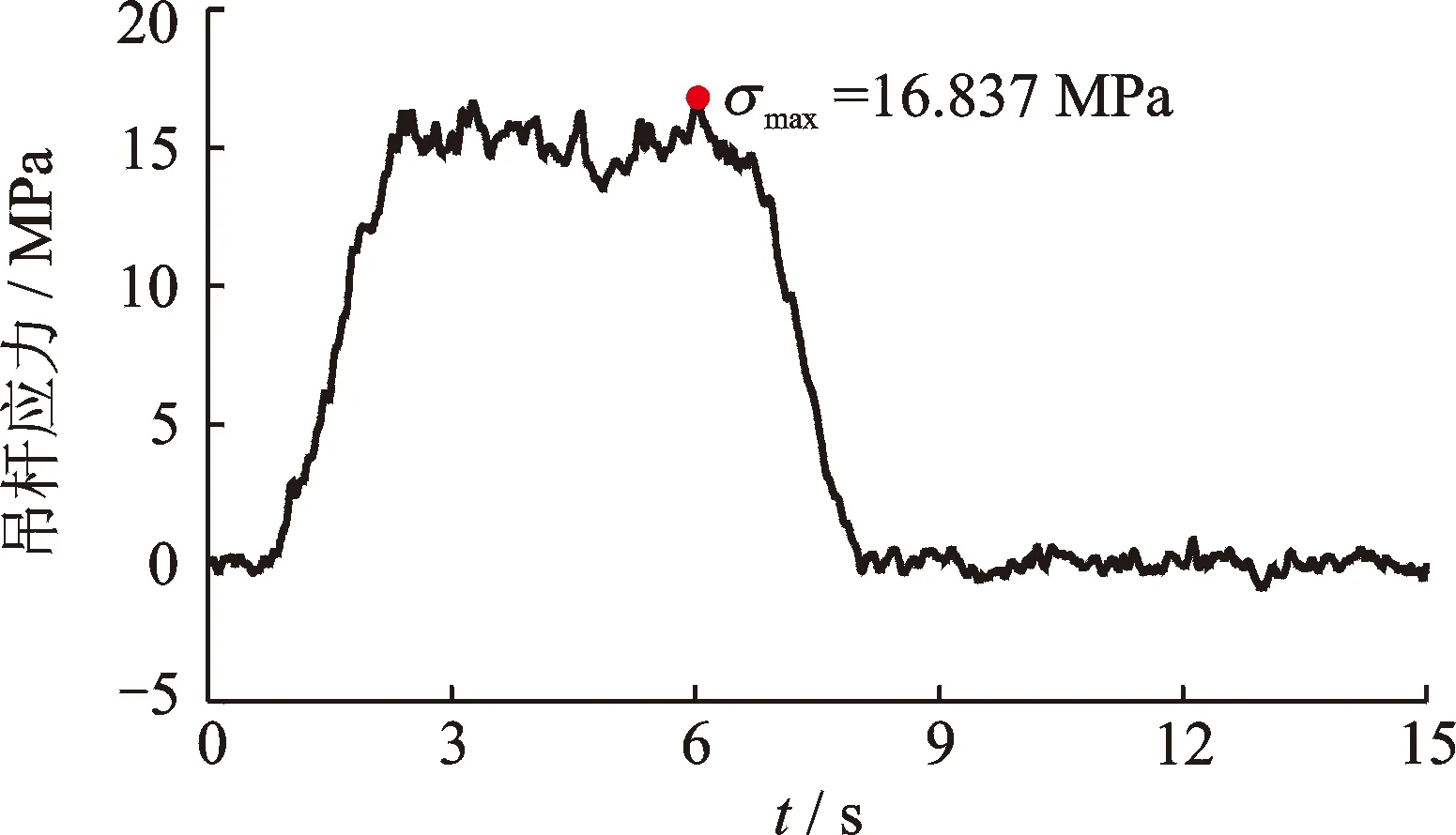
图10 工况2的5#吊杆应力

4 万宁桥理论模型及验证

采用有限元软件Ansys建立如图11所示的万宁桥轨道-桥梁有限元模型，其中:桥面板采用板单元SHELL 181模拟；拱肋、桥墩、横纵梁、横撑、钢轨和轨枕均采用梁单元BEAM188模拟；吊杆采用杆单元LINK180模拟；扣件、道砟和支座等均采用弹簧单元COMBIN14模拟。为防止钢轨和轨枕发生刚体转动，分别约束了钢轨的Rotx和轨枕的Roty方向自由度，桥墩墩顶采用刚性支座，墩底固结。为模拟列车上桥时的初始振动状态，在桥梁两端各添加了28.5 m长的轨道延长段。考虑配筋率的影响，混凝土主梁弹性模量为3.99×1010Pa，密度为2 973 kg/m3，拱肋弹性模量为3.91×1010Pa，密度为2 625 kg/m3，二者泊松比均为0.3，桥墩和轨枕采用C50混凝土。扣件及道砟参数如表2所示。

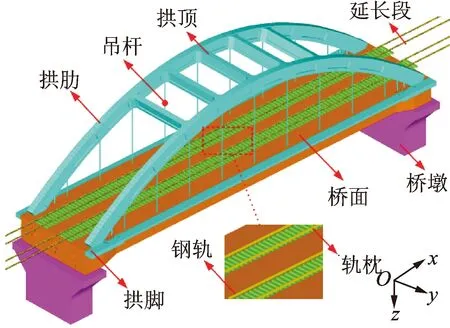
图11 万宁桥有限元模型

表3给出了万宁桥前10阶自振频率和振型的有限元计算结果，其中主梁竖弯自振频率为3.149 Hz，与试验测试的自振频率3.373 Hz相比，误差为6.6%，表明万宁桥有限元模型动力特性与实桥吻合较好。由图12可以看出，拱肋、主梁分别在第1、第5阶发生横弯，拱肋率先发生横向弯曲，表明拱肋横向刚度小于主梁横向刚度。

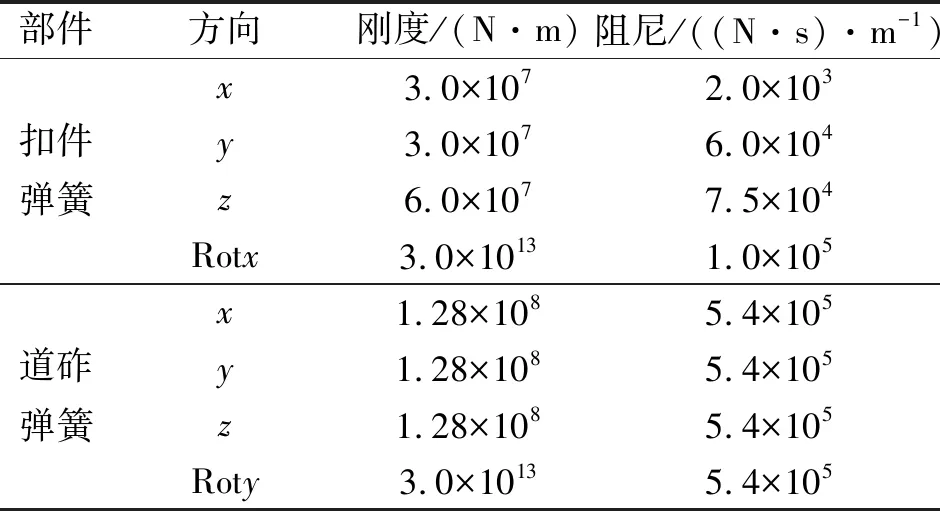
表2 万宁桥弹簧参数

表3 万宁桥自振特性

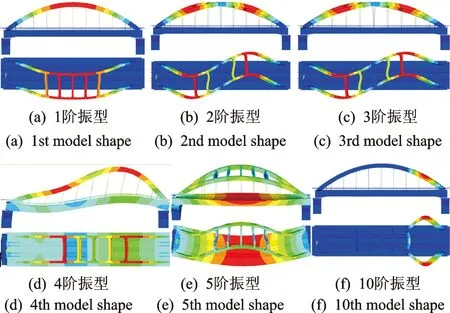
图12 万宁桥主要振型图

结合实际线路情况，根据1.1节所述理论建立了万宁桥的列车-轨道-桥梁耦合系统模型，CRH1A型列车编组为5M3T(MTMMTMTM，M为动车，T为拖车)，车辆参数如表4所示。采用德国低干扰轨道不平顺谱样本，积分步长取0.001 s，以表1中对应的行车工况计算桥梁的动力响应。

表4 车辆参数

图13给出了万宁桥现场试验测试值和列车-轨道-桥梁耦合系统模型计算结果的对比。图13(a)为工况1下CD1测点的位移时程曲线，由图可以看出，二者的位移时程曲线变化规律基本一致，试验和计算位移最大值分别为0.893和0.972 mm，二者相对误差为8.8%，表明模型计算结果与实际情况比较吻合。图13(b)为行车侧5#吊杆动应力的时程曲线，其中试验和计算吊杆应力最大值分别为16.730 和15.512 MPa，二者相对误差为7.28%，而应力变化规律基本一致，试验和计算吊杆应力冲击系数分别为0.085和0.079，二者的相对误差为7.06%。综上所述，基于万宁桥的列车-轨道-桥梁耦合系统计算模型基本正确。

图13 试测值与计算值对比图

5 吊杆应力冲击系数分析

为进一步研究不同行车条件对桥梁吊杆应力冲击系数的影响，基于列车-轨道-桥梁耦合系统模型进行了吊杆应力冲击系数的影响参数研究。

5.1 车速的影响

采用德国低干扰轨道不平顺谱，积分步长取0.001 s，考虑编组为5M3T的CRH1A型列车以50～350 km/h(按25 km/h递增)之间的13种速度单线行驶过桥，研究车速对吊杆应力冲击系数的影响。

从图14给出的行车侧吊杆动应力最大值可以看出，桥梁左右两端的吊杆动应力呈现均匀的对称性，中部吊杆动应力最大值大于两端吊杆动应力最大值，吊杆动应力最大值随车速的增加呈增大的趋势，中部吊杆动应力最大值受车速影响较为显著。

图14 不同车速下的吊杆动应力最大值

根据对称性，图15仅给出了1#～5#吊杆应力冲击系数随车速的变化规律。由图可以看出，整体上吊杆应力冲击系数随车速增加而增大，其中车速为300 km/h时吊杆动应力和冲击系数均显著增大。

图15 不同车速下的吊杆应力冲击系数

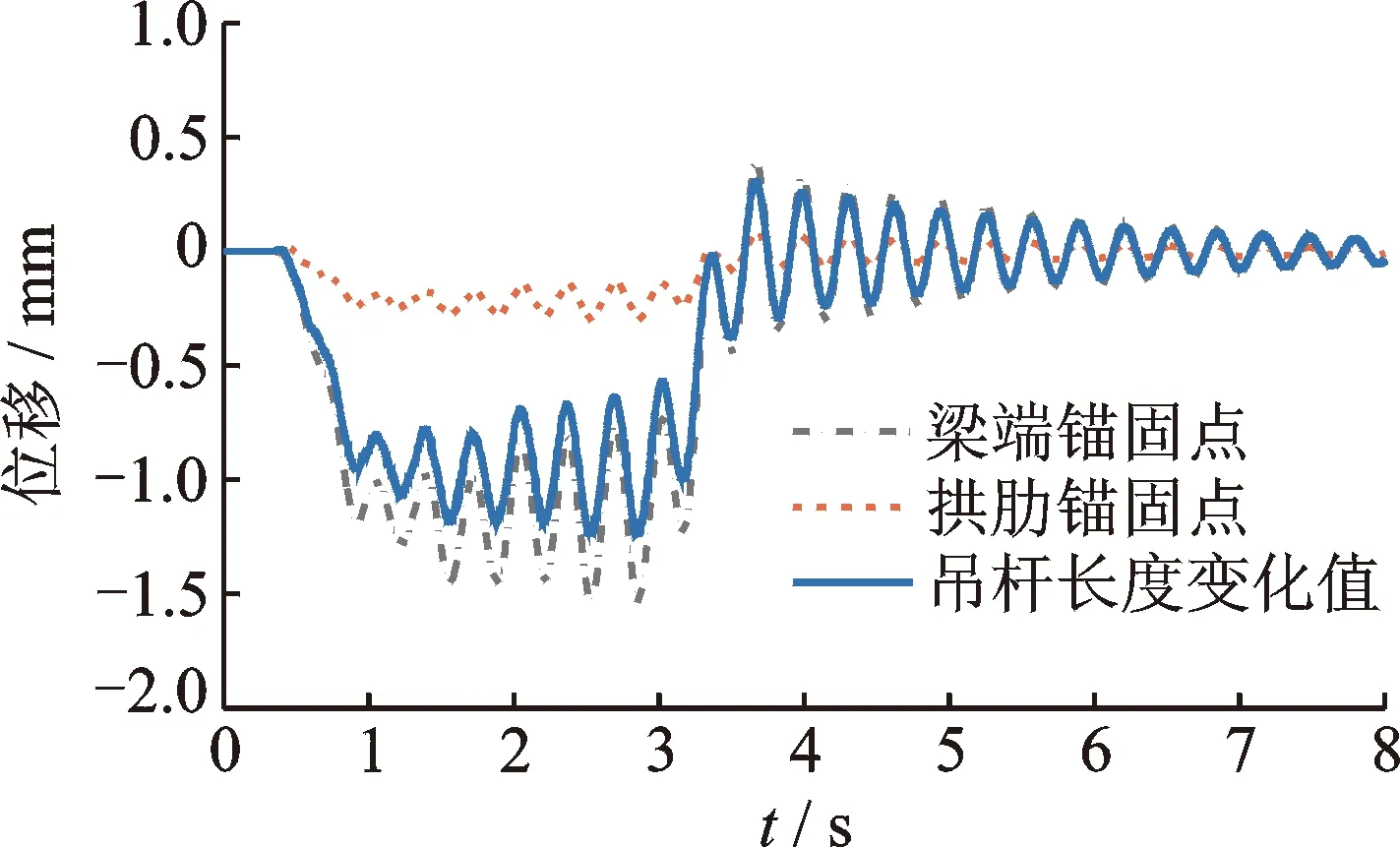
图16 300 km/h时5#吊杆两端位移时程曲线

图16为跨中5#吊杆梁端和拱肋锚固点的竖向位移时程曲线以及由此计算的吊杆长度变化值，可以看出列车以300 km/h的速度过桥时，引起主梁位移振幅不断增大，但拱肋位移振幅变化不如主梁明显，从而导致吊杆长度变化值显著增加。根据文献[21]的桥梁共振车速计算公式可知，对于CRH1A型列车来说，固定间距系列移动荷载作用下竖向共振车速可以表示为

vbr=3.6fbndv/i=302.68 km/h

(8)

其中：vbr为引起桥梁共振的列车临界车速；i为乘子，这里i=1；dv为车辆全长，CRH1A型列车单节车长为26.7 m；fbn为桥梁第n阶竖向自振频率。

万宁桥1阶竖向自振频率fb1=3.149 Hz。因此，当车速为300 km/h时，列车激励引起桥梁产生共振响应，导致吊杆应力和冲击系数均显著增大。

5.2 轨道不平顺的影响

选取与5.1节相同的行车条件，采用德国低干扰轨道谱作为初始轨道不平顺样本，将样本幅值进行缩放，在原始样本的基础上乘以0，0.5，1.0，1.5和2.0的缩放系数，分别代表最好、较好、初始、较差和最差的轨道平顺度[22]，研究轨道不平顺对吊杆应力冲击系数的影响。图17给出了不同轨道平顺性状态下行车侧吊杆的最大动应力σdmax和最大静应力σsmax，图18给出了相应吊杆的应力冲击系数。

图17 不同轨道平顺度下的吊杆应力

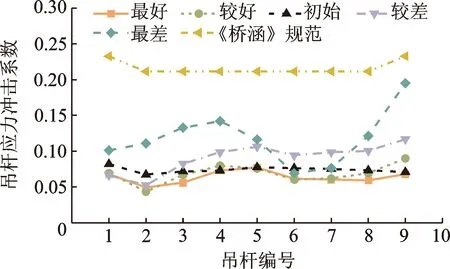
图18 不同轨道平顺度下的吊杆应力冲击系数

由图17可知，随着轨道平顺性的劣化，吊杆动应力最大值呈增加趋势，中部吊杆动应力最大值较端部吊杆增加更为显著。由图18可知，吊杆应力冲击系数随轨道平顺性的劣化而增大。初始状态下吊杆应力冲击系数最大值仅为0.082，小于规范设计值的0.233，可见初始状态下的高速铁路轨道不平顺对吊杆应力冲击系数的影响满足规范要求。

6 结 论

1) 地基微波雷达作为一种新型非接触式测试方法，能方便有效地测试列车作用下桥梁动挠度和吊杆动应力变化。

2) 拱桥吊杆应力分布具有对称性，跨中吊杆动应力最大值大于两端吊杆动应力最大值。从整体上看，吊杆动应力和应力冲击系数均随着车速的增加而增大，当车速为300 km/h时车辆和桥梁发生共振，导致吊杆应力大幅增加，因此需严格控制车速，避免发生共振。

3) 在设计车速和德国低干扰轨道谱条件下，CRH1A型动车组实际运营引起的吊杆应力冲击系数远小于规范值，整体上吊杆应力冲击系数随轨道平顺性的劣化而增加。实际运营时，应保障轨道平顺度，减少车辆产生的冲击作用，提高吊杆寿命。