采用改进模糊神经网络PID控制的移动机器人运动误差研究
2019-12-31许洋洋薛东彬
许洋洋,王 莹,薛东彬
(1.郑州工业应用技术学院 机电工程学院,河南 郑州 451150; 2.河南工业大学 机电工程学院,河南 郑州 450007)
移动机器人可以代替人类手工劳动,从而加快了工业的迅速发展.移动机器人具有许多优点[1-2]:① 可以连续生产劳动,成本低;② 生产效率高,运动精度高;③ 能够减少人员伤亡.因此,移动机器人在航天、海洋、医疗及煤矿等许多领域得到了广泛的应用.随着科技的改进,对移动机器人智能化程度要求也越来越高,而自动调整移动机器人运动轨迹精度是衡量移动机器人性能的重要指标之一.移动机器人在运动过程中,如果环境恶劣多变,运动轨迹就会发生偏离,导致运动轨迹产生较大的误差,有可能造成重大的经济损失.因此,研究移动机器人运动轨迹控制方法,对于促进机器人技术的发展具有重要意义.
当前,移动机器人控制技术吸引了许多学者的关注,并对其进行了研究.例如:文献[3-4]研究了移动机器人模糊PID控制方法,给出了机器人电机驱动模型,采用模糊推理来调节PID控制参数,通过仿真验证移动机器人路径跟踪误差,从而提高了移动机器人运动控制精度.文献[5-6]研究了移动机器人神经网络控制方法,采用RBF神经网络对控制系统进行在线辨识和反馈,通过李雅普诺夫函数对控制系统的稳定性进行证明,采用仿真验证移动机器人跟踪效果,降低了移动机器人路径跟踪误差.文献[7-8]研究了移动机器人滑模控制方法,建立移动机器人简图模型,给出了电机驱动数学模型,设计了滑模控制器并对其稳定性进行证明,抑制了控制系统的振动现象,实现移动机器人路径跟踪的精确性.以往研究的移动机器人容易受到外界波形的干扰,对此,在传统PID控制基础上,采用模糊神经网络PID控制方法.引用粒子群算法并进行改进,通过改进粒子群算法优化模糊神经网络PID控制参数.通过数学软件Matlab对移动机器人跟踪误差进行仿真实验,为提高移动机器人运动轨迹精度提供理论依据.
1 机器人模型
机器人简图模型如图1所示,通过质点运动分析可以推导出移动机器人运动学模型为
(1)
式中:v为移动机器人相对坐标系下的线速度;ω为移动机器人相对坐标系下的角速度;x′为移动机器人绝对坐标系下X方向的线速度;y′为移动机器人绝对坐标系下Y方向的线速度;θ′为移动机器人绝对坐标系下的角速度.

图1 移动机器人简图Fig.1 Sketch of mobile robot
根据拉格朗日定理,可以得到移动机器人动力学方程式[9]为
(2)
式中:q为位姿向量;M(q)为对称正定矩阵;Vm(q,q′)为向心力矩阵;F(q)为摩擦力矩阵;G(q)为重力矩阵;τd为未知干扰矩阵;A(q)为约束矩阵;B(q)为输入变换矩阵;τ为机器人转矩.
对于平面移动机器人,G(q)=0,A(q)q′=0,对式(2)进行简化,得
(3)
由于外界环境的影响,Mq和Vq的精确值无法得到.因此,可以用不确定部分构成,其方程式为
(4)
式中:Mq 0和Vq 0为确切值;ΔMq和ΔVq为不确定值.
假设:
(5)
则可以推导出
(6)
式中:ξq为平面结构不确定值的总和.
假设轨迹运动参数位置为qr=[xryrθr],参考速度为vr=[v0rω0r]T,找出平滑速度vc,令
(7)
由式(5)计算力矩输入τ,从而推导出t→∞时,v→vc.
机器人跟踪误差定义为
(8)
式中:Te为坐标变换矩阵.
运动学控制率方程式为
(9)
式中:ki>0(i=1,2,3).
辅助速度误差定义为
(10)
当ξq=0时,可以推导出非线性反馈控制方程式为
(11)

将式(8)代人式(5),可以得到
(12)
当ξq≠0时,则控制方法存在偏差较大.因此,研究一种能够自适应在线调整控制方法是非常必要的.
2 改进PID控制
2.1 PID控制
PID控制采用线性控制方式,其控制规律[10]为
(13)
式中:kp为比例系数;ki为积分系数;kd为微分系数;u(k)为控制器输出值;e(k)和e(k-1)为第k和k-1次输入的误差值;T为采用周期;Ti为积分时间常数;Td为微分时间常数.
PID控制采用比例、积分和微分线性组合很难达到最佳控制效果.对此,采用模糊神经网络PID控制器,建立输入误差、误差变化率与控制器参数组成关系式为
(14)
式中:f1,f2,f3为模糊神经网络;e为误差;ec为误差变化率.
采用模糊神经网络PID控制流程如图2所示.
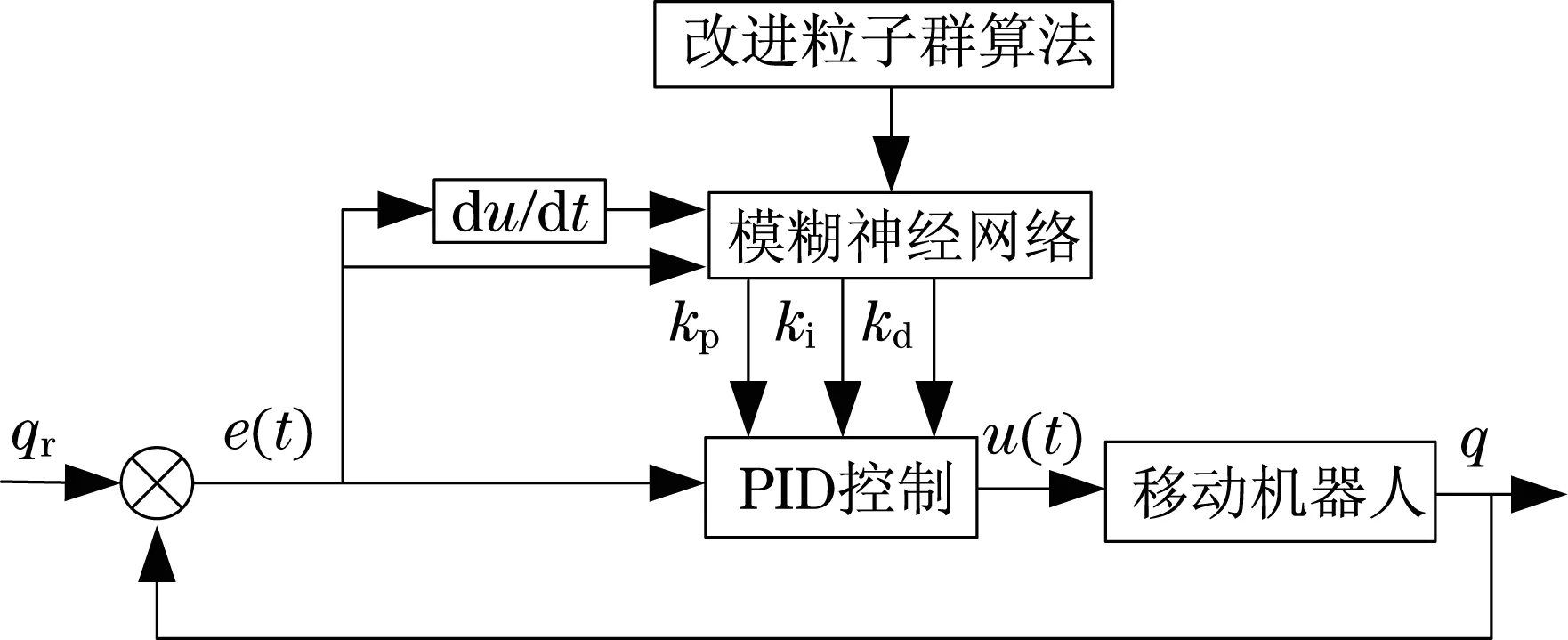
图2 模糊神经网络PID控制Fig.2 Fuzzy neural network PID control
2.2 模糊神经网络
模糊神经网络包括输入层、模糊化层、模糊推理层和输出层4个部分,其结构如图2所示.输入层采用二维输入,输入量为误差e和误差变化率ec,输出层采用3层神经网络结构.

图3 模糊神经网络Fig.3 Fuzzy neural network
模糊神经网络输入层和输出层关系如下:
输入层计算公式为
(15)
模糊化层采用高斯隶属度函数,其计算公式[11]为
(16)
式中:n为模糊子集个数;cij为隶属度函数中心值;bij为隶属度函数宽度.
模糊推理层计算公式[11]为
(17)
输出层计算公式为
(18)
式中:ωij为权值系数.
输出层输出的PID控制参数为
(19)
采用神经网络网络算法对隶属度函数中心值、宽度值和权值进行在线修正[11],方程式为
(20)
式中:E(k)为性能评价指标函数;λ为学习速率;η为惯性系数.
2.3 改进粒子群算法
粒子群算法是模拟鸟群捕食行为的一种群体智能优化算法.在N维搜索空间中,将粒子对应于优化问题,粒子的位置为Xi=(xi1,xi2,…,xiN),飞行速度为Vi=(vi1,vi2,…,viN).在搜索最优解过程中,粒子的速度和位置更新公式[12]为
式中:c1,c2为学习因子;r1,r2为随机数;Vi(t),Vi(t+1)分别为粒子t和t+1时刻的速度;Xi(t),Xi(t+1)分别为粒子t和t+1时刻的位置;P(t)为当前最优值;G(t)为全局最优值.
为了加快粒子群算法的收敛速度,粒子群算法速度修改为
(23)
(24)
3 误差仿真及分析
为了验证改进模糊神经网络PID控制效果,采用Matlab软件对移动机器人跟踪误差进行仿真.仿真参数设置如下:学习速率为λ=0.7,惯性系数为η=0.1,cij取值范围为[-4,4],bij取值范围为(0,4),网络权值ωij取值范围为[-1,1],种群大小为50,最大迭代次数为200,r1=r2=1,c1=c2=2.假设移动机器人在正弦波(y=2sin(2πt))干扰的环境中移动,移动机器人采用PID控制跟踪误差仿真结果如图4所示,移动机器人采用改进模糊神经网络PID控制跟踪误差仿真结果如图5所示.
由图4可知:采用传统PID控制方法,移动机器人实际运动轨迹与理论运动轨迹偏离较大.由图5可知:采用改进模糊神经网络PID控制方法,移动机器人实际运动轨迹与理论运动轨迹偏离较小.移动机器人在复杂环境中,容易受到外界环境的干扰,传统PID控制方法很难适应多变的复杂环境.采用改进模糊神经网络PID控制方法,能够对多变的环境进行在线调节PID控制参数,输出最优控制参数,从而保持控制系统运动的稳定性.因此,采用改进模糊神经网络PID控制方法,能够提高移动机器人运动轨迹跟踪精度.

图4 PID控制误差Fig.4 PID control error

图5 改进PID控制误差Fig.5 Improve PID control error
4 结论
针对移动机器人运动轨迹偏离误差较大问题,采用改进模糊神经网络PID控制方法,并对控制误差进行仿真验证,主要结论如下:① 移动机器人采用传统PID控制方法,与理论轨迹偏离误差较大,而采用改进模糊神经网络PID控制方法,与理论轨迹偏离误差较小.② 改进模糊神经网络PID控制方法,能够抑制外界波形的干扰,在线调节PID控制参数,维持控制系统的稳定性.③ 改进粒子群算法搜索速度快,能够快速地对PID控制系统做出反应,有效地降低移动机器人运动轨迹产生的偏差.
